Известия РАН. Серия физическая, 2019, T. 83, № 11, стр. 1455-1460

ВВЕДЕНИЕ

В основе многих физических методов локального анализа свойств твердого тела, а также некоторых технологических процессов, лежит бомбардировка исследуемого объекта пучком электронов киловольтных энергий [1–3]. При этом при облучении образца сфокусированным электронным пучком (электронным зондом) в месте его падения на мишень выделяется значительная энергия, что может привести к повышению локальной температуры мишени [4, 5] и, как следствие, к возможной необходимости учета этого явления при проведении количественных исследований. Учет нагрева проводящей мишени может быть особенно важен при использовании современной электронно-зондовой технологии, поскольку эффективный диаметр электронного пучка, взаимодействующего с полупроводниковой мишенью, может достигать 1–2 нм. При этом плотность энергии, выделяемой электронным пучком в мишени, может колебаться в пределах от 10 до 1000 Вт ⋅ см^–3, а характерный размер (диаметр) микрообъема потерь энергии электронами пучка не превышает 1 или 1.5 мкм [4, 5]. Таким образом, когда мишень облучается остро сфокусированным электронным пучком, нагрев образца может быть значительным и это может привести к увеличению локальной температуры и необходимости учитывать этот эффект при проведении количественных исследований [6]. Экспериментальное определение температуры нагрева сильно осложнено малым размером области генерации тепла, вследствие чего получаемые результаты имеют невысокую точность и могут рассматриваться лишь как качественные. Поэтому особую ценность на практике приобретают расчетные оценки величины нагрева электронным зондом, основанные на решении уравнения теплопроводности [4, 5, 7].

ПОСТАНОВКА ЗАДАЧИ

Ранее методами математического моделирования нами проведены расчеты нагрева полупроводниковых мишеней электронным зондом [8–11], а также получены предварительные результаты использования разработанного метода для оценки рассеяния энергии электронами и нагрева металлической мишени [12]. Такие исследования были продолжены, и в настоящей работе объектами исследований являются однородные металлические мишени. При этом, как и ранее, в качестве функции генерации источника тепла используется модель, основанная на возможности раздельного количественного описания вклада энергии поглощенными в мишени и обратно рассеянными электронами [13, 14]. Эта модель может быть успешно использована для проведения количественных расчетов для широкого класса материалов (практически от Al по Pt) в широком диапазоне энергий первичных электронов (практически от единиц кэВ до 50 кэВ). Использование этой модели при проведении расчетов нагрева мишеней низкоэнергетичными электронами и электронными пучками средних энергий для различных проводящих мишеней и сравнение результатов расчетов для различных металлов является основной целью настоящей работы.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИЗУЧАЕМОГО ПРОЦЕССА

Температурное поле в проводящей мишени, облучаемой электронным зондом, в стационарном случае может быть вычислено при решения трехмерного дифференциального уравнения:

Здесь $\Delta T(x,y,z)$ = $T(x,y,z) - {{T}_{0}}$ – искомый нагрев мишени при воздействии электронного зонда, $T$ – температура образца в точке $(x,y,z)$ после установления стационарного режима под воздействием электронного пучка, ${{T}_{0}}$ – температура образца до воздействия электронного пучка, $k$ – коэффициент теплопроводности, а $P(x,y,z)$ – функция, описывающая потери энергии электронами зонда в мишени [13, 14]. Разность $\Delta T(x,y,z)$ должна удовлетворять следующим граничным условиям: $\mathop {\lim }\limits_{x \to - \infty } \Delta T = 0,$ $\mathop {\lim }\limits_{x \to + \infty } \Delta T = 0,$ $\mathop {\lim }\limits_{y \to - \infty } \Delta T = 0,$ $\mathop {\lim }\limits_{y \to + \infty } \Delta T = 0,$ $\mathop {\lim }\limits_{z \to + \infty } \Delta T = 0.$ В условиях, близких к вакууму, теплообменом с внешней средой можно пренебречь, поэтому можно задать следующее граничное условие: $\partial \Delta T{{(z = 0)} \mathord{\left/ {\vphantom {{(z = 0)} {\partial z}}} \right. \kern-0em} {\partial z}} = 0.$ Как и ранее [8, 9, 11], при проведении вычислительного эксперимента использовалось решение рассматриваемого уравнения теплопереноса, полученное с использованием функции Грина [7, 15].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В качестве функции генерации источника тепла использована модель, основанная на возможности раздельного количественного описания вклада энергии поглощенных в мишени и обратно рассеянных электронов [13, 14]:

Здесь начало координат совпадает с точкой падения электронного зонда на образец, ${{P}_{0}}$ – мощность пучка первичных электронов, ${{P}_{0}}$ = = ${{I{{E}_{0}}} \mathord{\left/ {\vphantom {{I{{E}_{0}}} {\left| {{{e}_{0}}} \right|}}} \right. \kern-0em} {\left| {{{e}_{0}}} \right|}},$ где $I$ и ${{E}_{0}}$ – ток и энергия электронного пучка, e₀ – заряд электрона; z_ms – глубина максимальных потерь энергии первичными электронами, испытавшими малоугловое рассеяние и поглощенными мишенью, ${{z}_{{ss}}}$ – глубина максимальных потерь энергии обратно рассеянными электронами, ${{z}_{{ss}}} = {{Z}^{{{{ - {\text{1}}} \mathord{\left/ {\vphantom {{ - {\text{1}}} 3}} \right. \kern-0em} 3}}}}{{z}_{{ms}}},$ Z– эффективный порядковый номер материала мишени; η – коэффициент обратного рассеяния электронов пучка, ${\eta } = \left( {{{1.085a{\text{e}}} \mathord{\left/ {\vphantom {{1.085a{\text{e}}} {{{{\pi }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{z}_{{ms}}}}}} \right. \kern-0em} {{{{\pi }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{z}_{{ms}}}}}} \right)$ $\int_0^z {\exp \left[ {{{ - {{{\left( {z - {{z}_{{ss}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {z - {{z}_{{ss}}}} \right)}}^{2}}} {z_{{ss}}^{2}}}} \right. \kern-0em} {z_{{ss}}^{2}}}} \right]} dz,$ a = = 0.024(Z  ²/A), e – основание натуральных логарифмов, при этом для массивной мишени ${\eta } = \int_0^\infty {{\eta }\left( z \right)} dz$ ≈ ${{0.024{\text{e}}{{Z}^{{1.67}}}} \mathord{\left/ {\vphantom {{0.024{\text{e}}{{Z}^{{1.67}}}} A}} \right. \kern-0em} A};$ $A$ – эффективная относительная атомная масса материала мишени. Параметры ${{a}_{1}}$ и ${{a}_{2}}$ определяются из соотношений $a_{1}^{2}$ = $z_{{ms}}^{2} + 0.72d_{b}^{2},$ $a_{2}^{2}$ = $0.25z_{{ss}}^{2} + 0.72d_{b}^{2},$ где ${{d}_{b}}$ – диаметр электронного зонда. Для киловольтных электронов слагаемое $0.72d_{b}^{2}$ намного меньше $z_{{ms}}^{{\text{2}}}$ и $0.25z_{{ss}}^{2},$ поэтому им можно пренебречь.

Математическое моделирование распределений температуры в объеме различных металлических мишеней проведено для энергий электронного зонда, характерных для электронно-зондовых технологий в диапазоне от 2 до 25 кэВ. Расчеты проведены для тока зонда 10^–7 А, который в определенном смысле можно считать граничным для различных электроннозондовых устройств: меньшие токи, в т.ч. меньшие на несколько порядков, являются характерными для растровых электронных микроскопов, а большие токи – для рентгеновских микроанализаторов. Рассчитанные распределения температуры по x и y для алюминия (легкий металл), меди (металл со средним атомным номером) и золота (тяжелый металл) представлены на рис. 1, 2 и 3. При расчетах использовались следующие значения коэффициентов теплопроводности: для алюминия k = 23 ⋅ 10^–5 Вт ⋅ мкм^–2 К^–1, для меди k = 4 ⋅ 10^–4 Вт ⋅ мкм^–2 К^–1, для золота k = 31.2 ⋅ · 10^–5 Вт ⋅ мкм^–2 К^–1 [16]. В этих расчетах z принимали равным глубине максимальных потерь энергии первичными электронами ${{z}_{{ms}}},$ таким образом распределения температуры на этой глубине отвечают максимальным ее значениям по глубине мишеней при соответствующих значениях x и y. Максимальные значения температуры отвечают меньшим энергиям, при этом наибольший нагрев реализуется для более плотных мишеней. Поскольку размер области торможения электронов пучка приблизительно обратно пропорционален четвертой степени начальной энергии электронов, здесь происходит существенное увеличение объемной плотности тепловой энергии, генерируемой в образце [4, 5]. На рис. 4, 5 и 6 приведены результаты расчетов распределений $\Delta T(z)$ в Al, Cu и Au соответственно при x и y, равных нулю; результаты этих расчетов позволяют наглядно оценить распределение температуры по глубине мишеней. С увеличением энергии первичных электронов значительно увеличивается область нагрева, причем с ростом порядкового номера полупроводника область взаимодействия электронного пучка уменьшается: меньше всего нагрев наблюдается для легкой мишени, алюминия, а больше всего нагревается тяжелый образец, золото; при x и y, равных нулю, температура во всех образцах достигает максимума на глубине (по оси z) около значения ${{z}_{{ms}}}.$ На рис. 7, 8 и 9 показаны зависимости величины наибольшего нагрева образцов от энергии первичных электронов для Al, Cu и Au соответственно. Анализ вклада в потери энергии рассмотренных двух групп электронов – поглощенных в мишени и обратно рассеянных – показал, что для тяжелых металлов характерной оказалась немонотонная зависимость $\Delta T({{E}_{0}}),$ объяснимая большей разницей в распределениях по глубине потерь энергии поглощенными в мишени и обратно рассеянными электронами.

Рис. 1.

Результаты моделирования распределения температуры по x и y в Al при z, равном глубине максимальных потерь энергии первичными электронами. Расчеты проведены для энергии электронов E₀ = 2 (а), 6 (б), 10 (в), 15 (г), 20 (д) и 25 кэВ (е) при токе зонда 10^–7 A.

Рис. 2.

Результаты моделирования распределения температуры по x и y в Cu при z, равном глубине максимальных потерь энергии первичными электронами. Расчеты проведены для энергии электронов E₀ = 2 (а), 6 (б), 10 (в), 15 (г), 20 (д) и 25 кэВ (е) при токе зонда 10^–7 A.

Рис. 3.

Результаты моделирования распределения температуры по x и y в Au при z, равном глубине максимальных потерь энергии первичными электронами. Расчеты проведены для энергии электронов E₀ = 2 (а), 6 (б), 10 (в), 15 (г), 20 (д) и 25 кэВ (е) при токе зонда 10^–7 A.

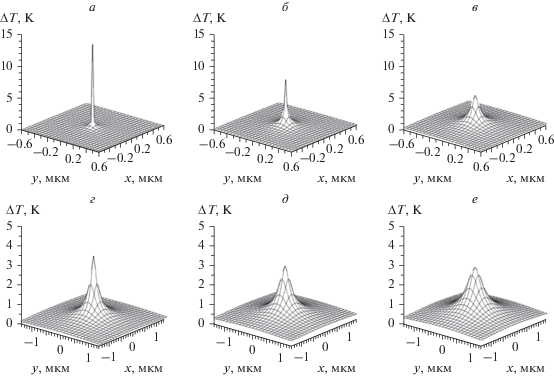
Рис. 4.

Результаты моделирования распределения температуры по z в Al при x и y, равными нулю. Расчеты проведены для энергии электронов E₀ = 2 (а), 6 (б), 10 (в), 15 (г), 20 (д) и 25 кэВ (е) при токе зонда 10^–7 A.

Рис. 5.

Результаты моделирования распределения температуры по z в Cu при x и y равными нулю. Расчеты проведены для энергии E₀ = 2 (а), 6 (б), 10 (в), 15 (г), 20 (д) и 25 кэВ (е) при токе зонда 10^–7 A.

Рис. 6.

Результаты моделирования распределения температуры по z в Au при x и y равными нулю. Расчеты проведены для энергии энергии E₀ = 2 (а), 6 (б), 10 (в), 15 (г), 20 (д) и 25 кэВ (е) при токе зонда 10^–7 A.

Рис. 7.

Результаты моделирования распределения зависимости максимальной температуры в Al от энергии первичных электронов (кривая 1); зависимости максимальной температуры от энергии поглощенных в мишени (кривая 2) и отраженных (кривая 3) первичных электронов. Расчеты проводились при токе зонда 10^–7 A.

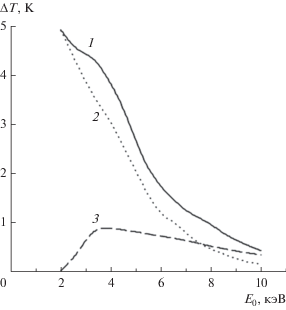
Рис. 8.

Результаты моделирования распределения зависимости максимальной температуры в Cu от энергии первичных электронов (кривая 1); зависимости максимальной температуры от энергии поглощенных в мишени (кривая 2) и отраженных (кривая 3) первичных электронов. Расчеты проводились при токе зонда 10^–7 A.

Рис. 9.

Результаты моделирования распределения зависимости максимальной температуры в Au от энергии первичных электронов (кривая 1); зависимости максимальной температуры от энергии поглощенных в мишени (кривая 2) и отраженных (кривая 3) первичных электронов. Расчеты проводились при токе зонда 10^–7 A.

ЗАКЛЮЧЕНИЕ

Методами математического моделирования проведена оценка нагрева металлических мишеней электронным зондом. Рассмотрение проведено для широкого диапазона металлов и энергий электронов. Вычислительный эксперимент позволил количественно оценить величину нагрева и некоторые закономерности этого процесса. Полученные результаты могут быть использованы при планировании эксперимента в электронно-зондовых технологиях.

Исследования выполнены при частичной финансовой поддержке грантами Российского фонда фундаментальных исследований (проект № 16-03-00515) и РФФИ и правительства Калужской области (проект № 18-41-400001).