Известия РАН. Серия физическая, 2019, T. 83, № 12, стр. 1594-1601
От микросекундного спинового эха к фемтосекундному электронному фотонному эху
И. С. Осадько *
Федеральное государственное бюджетное учреждение науки Институт спектроскопии
Российской академии наук
Москва, Россия
* E-mail: osadko@isan.troitsk.ru
Поступила в редакцию 20.06.2019
После доработки 20.07.2019
Принята к публикации 27.08.2019
Аннотация
Спиновое и фотонное эхо, возбуждаемые микро- и наносекундными электромагнитными импульсами, на протяжении более 70 лет являются предметом интенсивного изучения в работах разных авторов. Математической основой для описания таких эхо-эффектов служат уравнения Блоха. Однако при возбуждении эхо-сигнала с помощью ульракоротких фемтосекундных импульсов стало очевидным, что уравнения Блоха не в состоянии описать наблюдаемые эхо-сигналы. В работе показано, как теория для матрицы плотности, обобщающая уравнения Блоха, может описать фемтосекундную релаксацию поляризации и фемтосекундное фотонное эхо.
ВВЕДЕНИЕ
То обстоятельство, что в среде под воздействием электромагнитного поля наводится поляризация среды вытекало уже из уравнений Максвелла для электромагнитного поля в среде. Эта поляризация порождается внешним электромагнитным полем как в электронных степенях свободы среды, так и в ядерных. В классической работе Ф. Блоха [1] были выведены уравнения, описывающие динамику ядерной среды, находящейся в электромагнитном поле, получившие названия “уравнения Блоха”. Опираясь на эти уравнения можно было вычислить не только линейный эффект распада магнитной индукции (оптическую нутацию), но и нелинейные эффекты, типа микроволнового эха. Этот эффект состоит в том, что после возбуждения магнитной среды двумя электромагнитными импульсами, разделенными временным интервалом $\Delta t,$ появляется третий импульс – эхо, отделенный от второго импульса также интервалом $\Delta t.$ Эрвин Хан [2] показал, что такое микроволновое эхо действительно проявляется в эксперименте, и дал объяснение этого эффекта на основе уравнений Блоха.
Поскольку микроволновое эхо порождается спинами ядер, то оно получило название спинового эха. Хороший обзор эхо-явлений, описываемых уравнениями Блоха, приведен в монографии А.А. Калачева и В.В. Самарцева [3]. Было, например, обнаружено эхо-явление, происходящее и в электронной спиновой системе [4, 5]. Однако настоящий бум исследования различных нелинейных явлений, основанных на уравнениях Блоха, наступил после создания оптических источников когерентного света, типа рубинового лазера, построенного впервые в 1960 г. [6].
В 1963 г. в работе [7] авторами было показано, что эхо явления могут быть наблюдены и в оптическом диапазоне частот возбуждающего поля. И, действительно, такое эхо было зарегистрировано в рубине уже через год [8]. Поскольку эхо-сигнал наблюдали в оптическом диапазоне, он был назван фотонным эхом. Первые работы по фотонному эху в СССР были выполнены в Казани [9] и в Москве [10]. Казанский физико-технический институт (КФТИ) на долгие годы стал одним из ведущих институтов России в области спинового и фотонного эха.
Следует отметить, что математической основой для рассмотрения нелинейных явлений в среде, вызванных возбуждением среды электромагнитным полем, стали уравнения Блоха и их аналог, получивший название оптических уравнений Блоха. Эти уравнения были выведены для среды, в которой двухуровневые системы, взаимодействуют с электромагнитным полем и фононами среды. Физическое поведение таких двухуровневых систем детально рассмотрено в монографии Л. Аллана и Дж. Эберли [11], в которой среда описывается оптическими уравнения Блоха, а электромагнитное поле – уравнениями Максвелла.
Имея в виду рассмотрение в дальнейшем систем, которые требуют обобщения уравнений Блоха, оптические уравнения Блоха для электронных элементов матрицы плотности целесообразно записать в следующем виде
(1)
$\begin{gathered} {{{\dot {\rho }}}_{{10}}} = - i\left( {{{\Delta - i} \mathord{\left/ {\vphantom {{\Delta - i} {{{T}_{2}}}}} \right. \kern-0em} {{{T}_{2}}}}} \right){{\rho }_{{10}}} - \chi ({{\rho }_{0}} - {{\rho }_{1}}), \\ {{{\dot {\rho }}}_{{01}}} = \dot {\rho }_{{10}}^{ * },\,\,{{{\dot {\rho }}}_{1}} = {{ - {{\rho }_{1}}} \mathord{\left/ {\vphantom {{ - {{\rho }_{1}}} {{{T}_{1}} - \chi \left( {{{\rho }_{{10}}} + {{\rho }_{{01}}}} \right)}}} \right. \kern-0em} {{{T}_{1}} - \chi \left( {{{\rho }_{{10}}} + {{\rho }_{{01}}}} \right)}}, \\ {{{\dot {\rho }}}_{0}} = {{{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{\rho }_{1}}} {{{T}_{1}} + \chi \left( {{{\rho }_{{10}}} + {{\rho }_{{01}}}} \right)}}} \right. \kern-0em} {{{T}_{1}} + \chi \left( {{{\rho }_{{10}}} + {{\rho }_{{01}}}} \right)}}. \\ \end{gathered} $Здесь $\chi $ – частота Раби, описывающая взаимодействие электронного дипольного момента примесного центра с электромагнитным полем, а взаимодействие этого центра с фононами учтено введением двух эмпирических релаксационных констант: T1 – времени жизни возбужденного электронного уровня и Т2 – времени релаксации поляризации. Именно такие уравнения и послужили теоретической базой для многочисленных групп, которые исследовали различные типы фотонного эха. Такие исследования фотонного эха, проводившиеся в лаборатории В.В. Самарцева (КФТИ), нашли достаточно полное отражение в написанных им с соавторами монографиях [12, 13].
С началом исследований с применением фемтосекундных возбуждающих импульсов стало ясно, что распад поляризации, наведенной в твердотельном образце, не может быть описан с помощью уравнений (1). Например, из уравнений (1) вытекает, что при стационарном возбуждении населенность возбужденного уровня описывается лоренцианом c полушириной:
(2)
$\Delta {{\omega }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \frac{1}{{{{T}_{2}}}}\sqrt {1 + 4{{\chi }^{2}}{{T}_{1}}{{T}_{2}}} .$В системе, состоящей из магнитных моментов, для описания которых и создавались первоначально уравнения Блоха, индукция действительно описывается лоренцианом с полушириной (2). Однако система, состоящая, например, из молекулярных примесных центров, имеет более сложную форму оптической полосы, как это показано на рис. 1.
Рис. 1.
Перераспределение интенсивности в полосе флуоресценции молекулы перилена в н-гептане при повышении температуры. Взято из [14].
Очевидно, что поляризацию системы, которая имеет подобные полосы поглощения и флуоресценции, невозможно описать с помощью оптических уравнений Блоха. Какие же уравнения будут описывать динамику подобной системы мы и рассмотрим в данной статье.
ВЕКТОР БЛОХА ЭЛЕКТРОННО-КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ
Уравнения Блоха (1) построены для двухуровневой электронной системы. Четыре элемента матрицы плотности образуют четырех-компонентный вектор Блоха $\vec {\rho } = ({{\rho }_{{10}}},{{\rho }_{{01}}},{{\rho }_{{11}}},{{\rho }_{{00}}}).$ Влияние фононов описывают два релаксационных времени Т1 и Т2, введенных феноменологически.
Оптическая полоса флуоресценции примесного центра, изображенная на рис. 1, состоит из бесфононной линии (БФЛ), которая отвечает переходам между основным и возбужденным электронным состоянием, и фононного крыла (ФК), формируемого электронно-колебательным переходами. Следовательно, компоненты матрицы плотности такой электронно-колебательной системы должны зависеть как от электронных, так и колебательных индексов, т.е. вместо четырех-компонентного вектора Блоха надо рассматривать вектор Блоха $\vec {\rho } = ({{\rho }_{{ba}}},{{\rho }_{{ab}}},{{\rho }_{{aa{\kern 1pt} '}}},{{\rho }_{{bb{\kern 1pt} '}}})$ для электронно-колебательной системы. Здесь индексы $a$ и $b$ соответствуют электронно-колебательным состояниям электронно-невозбужденной и возбужденной системы. Число таких электронно-колебательных индексов бесконечно. Система уравнений для электронно-колебательного вектора Блоха $\vec {\rho } = ({{\rho }_{{ba}}},{{\rho }_{{ab}}},{{\rho }_{{aa{\kern 1pt} '}}},{{\rho }_{{bb{\kern 1pt} '}}})$ были выведены автором [15]. Она выглядит следующим образом:
(3)
$\begin{gathered} {{{\dot {\rho }}}_{{ba}}} = - i\left( {{{\Omega }_{{ba}}} - \frac{i}{{2{{T}_{1}}}}} \right){{\rho }_{{ba}}} + \sum\limits_{b{\kern 1pt} '} {{{\rho }_{{bb{\kern 1pt} '}}}{{\chi }_{{b{\kern 1pt} 'a}}} - } \sum\limits_{a'} {{{\chi }_{{ba{\kern 1pt} '}}}{{\rho }_{{a{\kern 1pt} 'a}}}} , \\ {{{\dot {\rho }}}_{{ab}}} = - i\left( {{{\Omega }_{{ab}}} - \frac{i}{{2{{T}_{1}}}}} \right){{\rho }_{{ab}}} + \sum\limits_{b{\kern 1pt} '} {\chi _{{ab{\kern 1pt} '}}^{ * }{{\rho }_{{b{\kern 1pt} 'b}}} - } \sum\limits_{a{\kern 1pt} '} {{{\rho }_{{aa{\kern 1pt} '}}}\chi _{{a{\kern 1pt} 'b}}^{ * }} , \\ {{{\dot {\rho }}}_{{bb{\kern 1pt} '}}} = - \sum\limits_a {\left( {{{\rho }_{{ba}}}\chi _{{ab{\kern 1pt} '}}^{ * } + {{\chi }_{{ba}}}{{\rho }_{{ab{\kern 1pt} '}}}} \right)} - i\left( {{{\Omega }_{{bb{\kern 1pt} '}}} - \frac{i}{{{{T}_{1}}}}} \right){{\rho }_{{bb{\kern 1pt} '}}}, \\ {{{\dot {\rho }}}_{{aa{\kern 1pt} '}}} = \sum\limits_b {\left( {\chi _{{ab}}^{ * }{{\rho }_{{ba{\kern 1pt} '}}} + {{\rho }_{{ab}}}{{\chi }_{{ba{\kern 1pt} '}}}} \right)} + \\ + \,\,\frac{1}{{{{T}_{1}}}}\sum\limits_{bb{\kern 1pt} '} {\left\langle {a{\text{|}}b} \right\rangle } {{\rho }_{{bb{\kern 1pt} '}}}\left\langle {b{\kern 1pt} '{\text{|}}a{\kern 1pt} '} \right\rangle - i{{\Omega }_{{aa{\kern 1pt} '}}}{{\rho }_{{aa{\kern 1pt} '}}}, \\ \end{gathered} $(4)
$\begin{gathered} {{\Omega }_{{ba}}} = \Omega + {{\Omega }_{b}} - {{\Omega }_{a}},\,\,\,\,{{\Omega }_{{bb{\kern 1pt} '}}} = {{\Omega }_{b}} - {{\Omega }_{{b{\kern 1pt} '}}}, \\ {{\Omega }_{{aa{\kern 1pt} '}}} = {{\Omega }_{a}} - {{\Omega }_{{a{\kern 1pt} '}}},\,\,{{\chi }_{{ab}}} = \frac{1}{\hbar }\left\langle {a{\text{|}}\vec {d}{\text{|}}b} \right\rangle \vec {E}(\vec {r},t). \\ \end{gathered} $Здесь Ωb и Ωa – частоты фононов в возбужденном и основном электронном состоянии примесного центра, соответственно; $\vec {d}$ – дипольный момент электронного перехода. Система уравнений (3) содержит частоты лазерных мод в функции поля $\vec {E}(\vec {r},t).$ Поэтому она позволяет рассматривать возбуждение примесного центра и немонохроматическим светом, т.е. рассматривать нестационарные эффекты в примесном центре даже при ультракоротком лазерном возбуждении, когда спектральная ширина импульса может оказаться шире оптической полосы поглощения. С такой ситуацией приходится сталкиваться при возбуждении молекул, например, лазерными импульсами с длительностью в несколько фемтосекунд.
Хотя система уравнений (3) существенно сложнее системы оптических уравнений Блоха, с ее помощью возможно проведение практических расчетов. Такие расчеты приведены ниже. В некоторых случаях для практических расчетов можно использовать упрощенный вариант системы (3), получающийся отбрасыванием недиагональных элементов матрицы плотности ρaa' и ρbb', которые описывают фазовую релаксацию в фононной подсистеме, В этом приближении мы можем ввести вероятности
(5)
${{p}_{a}} = \frac{{{{\rho }_{{aa}}}}}{{{{\rho }_{0}}}},\,\,{{p}_{b}} = \frac{{{{\rho }_{{bb}}}}}{{{{\rho }_{1}}}}$обнаружить соответствующее фононное состояние в основном и возбужденном электронном состоянии. Здесь
(6)
${{\rho }_{0}} = \sum\limits_a {{{\rho }_{{aa}}},} \,\,{{\rho }_{1}} = \sum\limits_b {{{\rho }_{{bb}}}} $суть вероятности найти примесную молекулу в основном или возбужденном электронном состоянии соответственно. Используя это приближение и производя суммирование по индексам a и b в уравнениях для ${{\rho }_{{aa}}}$ и ρbb, мы придем к следующей системе уравнений:
(7)
$\begin{gathered} {{{\dot {\rho }}}_{{ba}}} = - i\left( {{{\Omega }_{{ba}}} - \frac{i}{{2{{T}_{1}}}}} \right){{\rho }_{{ba}}} + {{\chi }_{{ba}}}({{p}_{b}}{{\rho }_{1}} - {{p}_{a}}{{\rho }_{0}}), \\ {{{\dot {\rho }}}_{{ab}}} = - i\left( {{{\Omega }_{{ab}}} - \frac{i}{{2{{T}_{1}}}}} \right){{\rho }_{{ba}}} + \chi _{{ab}}^{ * }({{p}_{b}}{{\rho }_{1}} - {{p}_{a}}{{\rho }_{0}}), \\ {{{\dot {\rho }}}_{1}} = - \sum\limits_{a,b} {\left( {\chi _{{ab}}^{ * }{{\rho }_{{ba}}} + {{\chi }_{{ba}}}{{\rho }_{{ab}}}} \right)} - \frac{{{{\rho }_{1}}}}{{{{T}_{1}}}}, \\ {{{\dot {\rho }}}_{0}} = \sum\limits_{a,b} {\left( {\chi _{{ab}}^{ * }{{\rho }_{{ba}}} + {{\chi }_{{ba}}}{{\rho }_{{ab}}}} \right)} + \frac{{{{\rho }_{1}}}}{{{{T}_{1}}}}. \\ \end{gathered} $Эту более простую систему уравнений можно применять вместо более сложной системы уравнений (3) при расчете наведенной поляризации и трехимпульсного фотонного эха, если расчет этих эффектов ведется в первом неисчезающем приближении по взаимодействию со светом.
Хотя уравнения (3) и (7) для обобщенного вектора Блоха были выведены еще в 1990 г., их использование на практике стало актуальным только после появления фемтосекундных лазеров в лабораториях. Последние достижения в работе с фемтосекундными лазерами, реализованные в Санкт-Петербургском государственном университете информационных технологий и оптики и в Казанском физико-техническом институте изложены в монографии [16]. Другой разновидностью метода фотонного эха, в которой фемтосекундное временное разрешение достигается за счет использования широкополосных лазерных импульсов, является некогерентное фотонное эхо [17–20]).
ТЕОРИЯ ФОРМЫ ОПТИЧЕСКОЙ ПОЛОСЫ ПРИМЕСНОГО ЦЕНТРА
Для того, чтобы рассматривать поляризацию системы с полосами флуоресценции типа изображенных на рис. 1, мы должны рассмотреть детально взаимодействие таких примесных центров с фононами. Молекулярные примесные центры, как правило, имеют низкую симметрию. Поэтому их электронные степени свободы не вырождены. Взаимодействие таких центров с фононами матрицы можно рассматривать в адиабатическом приближении [21, 22]. В этом приближении гамильтониан примесного центра имеет следующий вид в электронно-возбужденном (e) и основном (g) состоянии:
(8)
$\begin{gathered} {{H}^{e}}(R) = T(R) + (R + a)\frac{{{{U}^{e}}}}{2}(R + a), \\ {{H}^{g}}(R) = T(R) + R\frac{{{{U}^{g}}}}{2}R. \\ \end{gathered} $Электрон-фононным взаимодействием является разность адиабатических гамильтонианов:
где первое слагаемое есть константа, а второе и третье слагаемое(10)
$\begin{gathered} V(R) = (a{{U}^{e}})R = VR, \\ W(R) = R\frac{{{{U}^{e}} - {{U}^{g}}}}{2}R = R\frac{W}{2}R. \\ \end{gathered} $Описывают линейное и квадратичное по координатам R ядер франк-кондоновское (FC) взаимодействие.
Линейное FC-взаимодействие V(R) определяется сдвигом положений равновесия осцилляторов среды. Его влияние на форму полос поглощения и флуоресценции можно рассмотреть для произвольной величины сдвигов положений равновесия. Форма полос поглощения и флуоресценции имеют следующий вид
(11)
$\begin{gathered} {{k}^{g}}(\Delta ) = {{\chi }^{2}}\sum\limits_{a,b} {{{p}_{a}}\left\langle {a{\text{|}}b} \right\rangle \left\langle {b{\text{|}}a} \right\rangle } \times \\ \times \,\,\frac{{{1 \mathord{\left/ {\vphantom {1 {{{T}_{1}}}}} \right. \kern-0em} {{{T}_{1}}}}}}{{{{{(\Delta + {{\Omega }_{b}} - {{\Omega }_{a}})}}^{2}} + {{{({1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}})}}^{2}}}}, \\ {{k}^{e}}(\Delta ) = {{\chi }^{2}}\sum\limits_{a,b} {{{p}_{b}}\left\langle {a{\text{|}}b} \right\rangle \left\langle {b{\text{|}}a} \right\rangle } \times \\ \times \,\,\frac{{{1 \mathord{\left/ {\vphantom {1 {{{T}_{1}}}}} \right. \kern-0em} {{{T}_{1}}}}}}{{{{{(\Delta + {{\Omega }_{b}} - {{\Omega }_{a}})}}^{2}} + {{{({1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}})}}^{2}}}}. \\ \end{gathered} $Функция kg(Δ) определяет вероятность поглощения в единицу времени фотона частоты ω0, отстроенного на величину Δ = Ω – ω0 от резонансной частоты Ω, а функция ke(Δ) определяет вероятность вынужденного испускания фотона в единицу времени. Здесь $\chi $ – частота Раби, определяющая интенсивность взаимодействия электронного возбуждение примесного центра со светом возбуждающего лазера, ${{p}_{a}}$ и ${{p}_{b}}$ вероятности реализации начального колебательного состояния в основном и возбужденном электронном состоянии, а $\left\langle {a{\text{|}}b} \right\rangle $ интегралы Франка–Кондона функций гармонического осциллятора. Взяв эти интегралы для случая линейного FC-взаимодействия, для формы оптических полос приходим к следующему выражению [22]:
(12)
${{S}^{{g,e}}}(\omega ) = {{e}^{{ - {\varphi }(0,T)}}}\frac{{{1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}\pi }}} \right. \kern-0em} {2{{T}_{1}}\pi }}}}{{{{\Delta }^{2}} + {{{\left( {{1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}}} \right)}}^{2}}}} + {{\Psi }^{{g,e}}}(\Delta ).$Здесь $\Delta = \omega - \Omega .$ Первое слагаемое описывает бесфононную линию (БФЛ), а второе слагаемое определяет электрон-фононные фотопереходы и называется фононным крылом (ФК). ФК описывается следующим выражением:
(13)
$\begin{gathered} {{\Psi }^{{g,e}}}(\Delta ) = \sum\limits_{m = 1}^\infty {\Psi _{m}^{{g,e}}(\Delta )} = \\ = {{e}^{{ - {\varphi }(0,T)}}}\sum\limits_{m = 1}^\infty {\frac{1}{{m!}}} \int\limits_{ - \infty }^\infty {\frac{{d{{\nu }_{1}}}}{{2\pi }}\varphi ({{\nu }_{1}},T)...} \int\limits_{ - \infty }^\infty {\frac{{d{{\nu }_{m}}}}{{2\pi }}} \varphi ({{\nu }_{m}},T) \times \\ \times \,\,\frac{{{1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}\pi }}} \right. \kern-0em} {2{{T}_{1}}\pi }}}}{{{{{(\Delta \mp {{\nu }_{1}}... \mp {{\nu }_{m}})}}^{2}} + {{{\left( {{1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}}} \right)}}^{2}}}}, \\ \end{gathered} $(14)
$\begin{gathered} \varphi (\nu ,T) = \int\limits_{ - \infty }^\infty {\varphi (t,T){{e}^{{i{\nu }t}}}dt} = \varphi (\nu )(n(\nu ) + 1) + \\ + \,\,\varphi ( - \nu )n( - \nu ),\,\,\varphi (\nu ) = \sum\limits_{q = 1}^N {\frac{{a_{q}^{2}}}{2}\delta (\nu - {{\nu }_{q}}),} \\ n(\nu ) = \frac{1}{{\exp ({{\hbar \nu } \mathord{\left/ {\vphantom {{\hbar \nu } {kT}}} \right. \kern-0em} {kT}}) - 1}}. \\ \end{gathered} $Согласно формуле (12) БФЛ полосы флуоресценции и поглощения находятся в резонансе друг с другом, а их ширина при учете только линейного FC-взаимодействия определяется временем жизни T1 возбужденного электронного уровня. ФК в спектре поглощения и флуоресценции расположены зеркально симметрично относительно БФЛ и имеют одинаковую форму.
Учет влияния квадратичного взаимодействия W на форму оптических полос – довольно сложная операция, потому что это влияние нельзя рассматривать по теории возмущений [21, 23]. Дело в том, что квадратичное взаимодействие W изменит систему нормальных координат при электронном возбуждении. Поэтому частоты фононов в основном и возбужденном электронном состоянии будут разные: $\nu _{q}^{g}$ и $\nu _{q}^{e}.$ Если квадратичное взаимодействие рассматривать в формулах (11) по теории возмущений, то мы обнаружим, что в спектре флуоресценции появятся пики с частотами $\nu _{q}^{e},$ а спектре поглощения – с частотами $\nu _{q}^{g}.$ В эксперименте же будет противоположная картина. В спектре флуоресценции будут наблюдаться пики с частотами $\nu _{q}^{g},$ а спектре поглощения – с частотами $\nu _{q}^{e}.$ Такой результат может объяснить только такая теория, в которой взаимодействие W учитывается без использования теории возмущений. Это обстоятельство существенно усложняет учет влияния квадратичного взаимодействия.
Квадратичное электрон-фононное взаимодействие W, не изменяя принципиально спектральной картины, описанной выше: 1) нарушает симметрию ФК поглощения и флуоресценции, 2) приводит к дополнительному уширению БФЛ, заменяя величину ${1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}}$ в формулах (12) и (13) на следующее выражение
(15)
${1 \mathord{\left/ {\vphantom {1 {{{T}_{2}}}}} \right. \kern-0em} {{{T}_{2}}}} = {1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}} + {{\gamma }_{{el - ph}}}(T),$(16)
$\begin{gathered} {{\gamma }_{{el - ph}}}(T) = \\ = \int\limits_0^\infty {\frac{{d\omega }}{{2\pi }}\ln \left[ {1 + 4n(\omega )(n(\omega ) + 1){{W}^{2}}{{\Gamma }^{e}}(\omega ){{\Gamma }^{g}}(\omega )} \right]} , \\ \end{gathered} $(17)
$\begin{gathered} {{\Gamma }^{e}}(\omega ) = \frac{{{{\Gamma }^{g}}(\omega )}}{{{{{\left( {1 - W{{\Omega }^{g}}(\omega )} \right)}}^{2}} + {{{(W{{\Gamma }^{g}}(\omega ))}}^{2}}}}, \\ {{\Omega }^{g}}(\omega ) = \int\limits_0^\infty {\frac{{d\nu }}{\pi }\frac{{2\nu {{\Gamma }^{g}}(\nu )}}{{{{\omega }^{2}} - {{\nu }^{2}}}}} \\ \end{gathered} $есть спектральная плотность фононов в возбужденном электронном состоянии, выраженная через спектральную плотность Γg(ω) фононов в основном электронном состоянии. Сравнивая эти две функции, мы можем увидеть, какие изменения в фононной системе вызывает квадратичное FC-взаимодействие.
СВЕРХБЫСТРАЯ ОПТИЧЕСКАЯ ДЕФАЗИРОВКА
Бесконечномерные системы уравнений (3) и (7) для матрицы плотности содержат в себе информацию обо всей оптической полосе, т.е. о бесфононных и электронно-колебательных переходах. Поэтому она способна описать правильно и фазовую релаксацию.
Сверхбыструю фазовую релаксацию обычно наблюдают после прохождения через образец очень короткого лазерного импульса длительности Δt. Тогда, используя и начальные условия ${{\rho }_{0}}(0) = 1,$ ${{\rho }_{1}}(0) = \rho {}_{{ab}}(0)$ = ${{\rho }_{{ba}}}(0) = 0,$ находим из первых двух уравнений системы (7) следующие выражения для недиагональных элементов матрицы плотности:
(18)
${{\rho }_{{ba}}}(\Delta t) \cong \chi \Delta t\left\langle {b{\text{|}}a} \right\rangle {{p}_{a}} = \vartheta \left\langle {b{\text{|}}a} \right\rangle {{p}_{a}} = {{\rho }_{{ab}}}(\Delta t).$После прохождения лазерного импульса матричные элементы начнут изменяться со временем следующим образом:
(19)
$\begin{gathered} {{\rho }_{{ba}}}(t) = {{e}^{{ - i\left( {{\Omega } + {{{\Omega }}_{b}} - {{{\Omega }}_{a}} - \frac{i}{{2{{T}_{1}}}}} \right)t}}}{{\rho }_{{ba}}}(\Delta t), \\ {{\rho }_{{ab}}}(t) = {{e}^{{i\left( {{\Omega } + {{{\Omega }}_{b}} - {{{\Omega }}_{a}} + \frac{i}{{2{{T}_{1}}}}} \right)t}}}{{\rho }_{{ab}}}(\Delta t). \\ \end{gathered} $Среднее значение дипольного момента молекулы в момент времени t описывается стандартным выражением:
(20)
$d(t) = Tr\left\{ {\hat {d}\hat {\rho }(t)} \right\} = \sum\limits_{a,b} {\left\{ {{{d}_{{ab}}}{{\rho }_{{ba}}}(t) + {{d}_{{ba}}}{{\rho }_{{ab}}}(t)} \right\}} ,$(22)
${{S}^{g}}(t) = \sum\limits_{a,b} {{{p}_{a}}\left\langle {a{\text{|}}b} \right\rangle {{e}^{{ - i\left( {{{{\Omega }}_{b}} - {{{\Omega }}_{a}} - \frac{i}{{2{{T}_{1}}}}} \right)t}}}\left\langle {b{\text{|}}a} \right\rangle } ,$Как мы уже отмечали ранее, при учете квадратичного FC-взаимодействия затухание недиагональных матричных элементов определяется не константой ${1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}},$ а константой 1/T2 = = ${1 \mathord{\left/ {\vphantom {1 {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}} + {{\gamma }_{{el - ph}}}(T).$ Поэтому такую замену целесообразно сделать и в формуле (22). Тогда после вычисления сумм в формуле (22) мы приходим к следующему выражению:
(23)
$\begin{gathered} {{S}^{g}}(t) = \exp g(t) = \\ = \,\,\exp \left[ { - \frac{{\left| t \right|}}{{{{T}_{2}}}} + \varphi (t,T) - \varphi (0,T)} \right], \\ \end{gathered} $(24)
$\begin{gathered} \varphi (t,T) = \\ = \,\,\sum\limits_{q = 1}^N {\frac{{a_{q}^{2}}}{2}\left\{ {{{n}_{q}}\exp (i{{\nu }_{q}}t) + ({{n}_{q}} + 1)\exp ( - i{{\nu }_{q}}t)} \right\}} . \\ \end{gathered} $описывает влияние сдвигов положений равновесия на оптическую полосу. Здесь мы пренебрегаем влиянием квадратичного взаимодействия на функцию $\varphi (t,T).$ Подставляя формулу (23) в формулу (21), мы придем к следующему выражению для дипольного момента, квадрат модуля которого определяет интенсивность излучения поляризованной молекулы:
(25)
$\begin{gathered} d(t) = 2d\vartheta \exp \left( { - \varphi (0,T) + \operatorname{Re} \varphi (t,T) - \frac{{\left| t \right|}}{{{{T}_{2}}}}} \right) \times \\ \times \,\,\cos \left( {\Omega t + \operatorname{Im} \varphi (t,0)} \right). \\ \end{gathered} $Проанализируем последнюю формулу. Если линейное FC-взаимодействие отсутствует, то функция φ(t, T) = 0, и мы приходим к формуле, описывающей экспоненциальную дефазировку, которая вытекает и из уравнений Блоха. Если же линейное FC-взаимодействие не равно нулю, то Reφ(t, T) ≠ 0, т.е. появляется дополнительная дефазировка, вызванная этим взаимодействием. Эта дефазировка характеризуется функцией дефазировки φ(t, T). Функцию дефазировки, описываемую формулой (24), можно представить в следующем виде:
(26)
$\begin{gathered} \operatorname{Re} \varphi - i\operatorname{Im} \varphi = \int\limits_0^\infty {\varphi (\nu )(2n(\nu ) + 1)\cos \nu td\nu } - \\ - \,\,i\int\limits_0^\infty {\varphi (\nu )\sin \nu td\nu } , \\ \end{gathered} $(27)
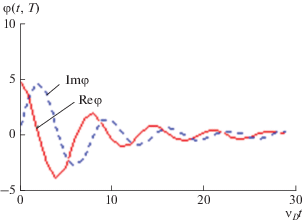
$\begin{gathered} \varphi (\nu ) = \varphi (0,0)9.857\frac{{{{\nu }^{3}}}}{{\nu _{D}^{{4.5}}}}\sqrt {{{\nu }_{D}} - \nu } , \\ 0 \leqslant \nu \leqslant {{\nu }_{D}}. \\ \end{gathered} $Здесь корень нужен для введения поправки в дебаевскую плотность состояний в высокочастотной области, функция связи с фононами линейна по частоте, а введение численного множителя гарантирует равенство интеграла от этой функции фактору Пекара–Хуанга φ(0, 0) при нулевой температуре. Напомним, что этот фактор определяет силу линейного FC-взаимодействия. На рис. 2 показано временное поведение функции дефазировки, рассчитанное по формуле (26) с учетом формулы (27). При t ≅ 30/νD функция дефазировки обращается в нуль. Типичное для органических растворов значение дебаевской частоты νD равно примерно 100 см–1, чему соответствует 30/νD ≅ 1.5 пс. Время Т2 при гелиевых температурах на пару порядков больше. Следовательно, неэкспоненциальная дефазировка, обусловленная линейным электрон-фононным взаимодействием происходит в сто раз быстрее экспоненциальной дефазировки, порожденной квадратичным электрон-фононным взаимодействием. Именно эта сверхбыстрая дефазировка и проявляет себя в фемтосекундном фотоном эхе.
ФЕМТОСЕКУНДНОЕ ФОТОННОЕ ЭХО
Фемтосекундное фотонное эхо было рассмотрено на основе временной эволюции электронно-колебательного вектора Блоха [24]. В системе уравнений (3) разобьем электронно-колебательный вектор Блоха на два вектора: $\vec {a} = ({{\rho }_{{ba}}},{{\rho }_{{ab}}})$ и $\vec {b} = ({{\rho }_{{bb{\kern 1pt} '}}},{{\rho }_{{aa{\kern 1pt} '}}}).$ Тогда систему уравнений (3) можно записать в следующем виде
Входящие в систему символы надо понимать следующим образом:
(28)
$\begin{gathered} {{{\hat {\chi }}}_{1}}\vec {b}(\tau ) = \vec {a}{\kern 1pt} '(\tau ) = \\ = \left( {\begin{array}{*{20}{c}} {\sum\limits_{b{\kern 1pt} '} {{{\rho }_{{bb{\kern 1pt} '}}}(\tau ){{\chi }_{{b{\kern 1pt} 'a}}}} - \sum\limits_{a{\kern 1pt} '} {{{\chi }_{{ba{\kern 1pt} '}}}{{\rho }_{{a{\kern 1pt} 'a}}}(\tau )} } \\ {\sum\limits_{b{\kern 1pt} '} {\chi _{{ab{\kern 1pt} '}}^{ * }{{\rho }_{{b{\kern 1pt} 'b}}}(\tau )} - \sum\limits_{a{\kern 1pt} '} {{{\rho }_{{aa{\kern 1pt} '}}}(\tau )\chi _{{a{\kern 1pt} 'b}}^{ * }} } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{\rho }_{{ba}}}(\tau )} \\ {{{\rho }_{{ab}}}(\tau )} \end{array}} \right), \\ \end{gathered} $(29)
$\begin{gathered} {{{\hat {\chi }}}_{2}}\vec {a}(\tau ) = \vec {b}(\tau ) = \\ = \left( {\begin{array}{*{20}{c}} { - \sum\limits_a {\left( {{{\rho }_{{ba}}}(\tau )\chi _{{ab{\kern 1pt} '}}^{ * } + {{\chi }_{{ba}}}{{\rho }_{{ab{\kern 1pt} '}}}(\tau )} \right)} } \\ {\sum\limits_b {\left( {\chi _{{ab}}^{ * }{{\rho }_{{ba{\kern 1pt} '}}}(\tau ) + {{\rho }_{{ab}}}(\tau ){{\chi }_{{ba{\kern 1pt} '}}}} \right)} } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{\rho }_{{bb{\kern 1pt} '}}}(\tau )} \\ {{{\rho }_{{aa{\kern 1pt} '}}}(\tau )} \end{array}} \right), \\ \end{gathered} $(30)
${{e}^{{{\hat {\omega }\tau }}}}\vec {a} = \left( {\begin{array}{*{20}{c}} {{{e}^{{{{{\varepsilon }}_{{ba}}}{\tau }}}}{{\rho }_{{ba}}}} \\ {{{e}^{{{{{\varepsilon }}_{{ab}}}{\tau }}}}{{\rho }_{{ab}}}} \end{array}} \right),$(31)
$\begin{gathered} {{\varepsilon }_{{ba}}} = - i({{\Omega + {{\Omega }_{{ba}}} - i} \mathord{\left/ {\vphantom {{\Omega + {{\Omega }_{{ba}}} - i} {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}}),\,\, - i( - \Omega + {{{{\Omega }_{{ab}}} - i} \mathord{\left/ {\vphantom {{{{\Omega }_{{ab}}} - i} {2{{T}_{1}}}}} \right. \kern-0em} {2{{T}_{1}}}}), \\ {{\Omega }_{{ab{\text{ }}}}} = {\text{ }}{{\Omega }_{{a{\text{ }}}}}--{\text{ }}{{\Omega }_{b}}. \\ \end{gathered} $Выражение для дипольного момента в момент времени $t = \tau + \tau {\kern 1pt} '$ описывается следующей формулой:
(32)
$d(t) = {{\vec {d}}^{ \bot }}\vec {a}(t) = {{\vec {d}}^{ \bot }}{{e}^{{{\hat {\omega }\tau }{\kern 1pt} {\text{'}}}}}{{\hat {\chi }}_{1}}{{\hat {\chi }}_{2}}{{e}^{{{\hat {\omega }\tau }}}}{{\hat {\chi }}_{1}}\vec {b}(0).$Перемножая матрицы в этом выражении, придем к следующему выражению для дипольного момента, определяющего интенсивность фотонного эха:
Фононные частоты Ωa и Ωb – суть собственные значения адиабатических гамильтонианов Hg и He. Принимая во внимание, что ${{d}_{{ab}}} = d\left\langle {a{\text{|}}b} \right\rangle ,$ ${{\chi }_{{ab}}} = \vartheta \left\langle {a{\text{|}}b} \right\rangle ,$ ${{\Omega }_{{ab}}} = {{\Omega }_{a}} - {{\Omega }_{b}},$ и заменяя частоты на эти гамильтонианы, мы получаем следующее выражение для дипольного момента:
(34)
$\begin{gathered} {{d}_{{2PE}}}(t) = 4d{{\vartheta }^{3}}{{e}^{{ - \frac{{{\tau }{\kern 1pt} {\text{'}} + {\tau }}}{{2{{T}_{1}}}}}}} \times \\ \times \,\,\operatorname{Re} \left\{ {{{e}^{{ - i{\Omega }({\tau }{\kern 1pt} {\text{'}} - {\tau })}}}{{{\left\langle {{{e}^{{ - i\frac{{{{H}^{g}}}}{\hbar }{\tau }}}}{{e}^{{i\frac{{{{H}^{e}}}}{\hbar }{\tau }}}}{{e}^{{i\frac{{{{H}^{g}}}}{\hbar }{\tau }{\kern 1pt} {\text{'}}}}}{{e}^{{ - i\frac{{{{H}^{e}}}}{\hbar }{\tau }{\kern 1pt} {\text{'}}}}}} \right\rangle }}_{g}}} \right\}, \\ \end{gathered} $(35)
$\begin{gathered} {{d}_{{2PE}}}(\tau {\kern 1pt} ' + \tau ) = 4d{{\vartheta }^{3}}{{e}^{{ - \frac{{{\tau } + {\tau }{\kern 1pt} '}}{{{{T}_{2}}}}}}}\,\, \times \\ \times \,\,\operatorname{Re} \left\{ {\exp [2g{\text{*}}(\tau ) + 2\operatorname{Re} g(\tau {\kern 1pt} ') - g{\text{*}}(\tau {\kern 1pt} ' + \tau )]} \right\}, \\ \end{gathered} $есть разность между функцией дефазировки $\varphi (t,T)$ и фактором Пекара–Хуанга, $\varphi (0,T),$ характеризующим силу линейного FC-взаимодействия.
Из формулы (35) следует, что при τ = τ' = 0 дипольный момент максимален, а с ростом τ он начинает убывать, стремясь к нулю. При τ $ \ll $ T2 уменьшение величины дипольного момента будет происходить за счет убывания величины функции дефазировки
(37)
$\varphi (t,T) = \int\limits_{ - \infty }^\infty {\varphi (\nu ,T){{e}^{{ - i{\nu }t}}}\frac{{d\upsilon }}{{2\pi }}} .$Функция дефазировки $\varphi (t,T)$ обращается в нуль на временном интервале порядка обратной частоты Дебая. Поэтому эту функцию следует назвать функцией быстрой дефазировки. При τ > T2 главную роль в убывании дипольного момента (дефазировке) начинает играть экспоненциальный множитель с константой T2. Константа $\varphi (0,T),$ называемая фактором Пекара–Хуанга, характеризует силу линейного Франк–Кондоновского взаимодействия.
При повышении температуры величина константы $\varphi (0,T)$ Пекара–Хуанга возрастает и поэтому БФЛ уменьшается, а интенсивность ФК возрастает, как показано на рис. 3.
Рис. 3.
Оптическая полоса при Т = 0.1TD (a), 0.3TD (б), TD (в). Фактор Пекара–Хуанга равен 0.7, Т2 = TD/30, TD = 210 K.

Оптическая полоса S, представленная на рис. 3, рассчитана по формулам (12) и (13) с использованием следующей функции взвешенной плотности фононных состояний
(38)
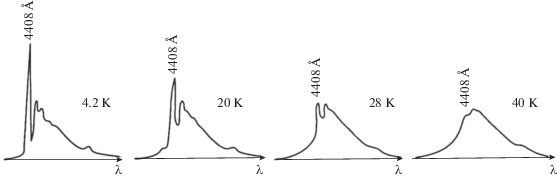
$\varphi (\nu ) = 0.7 \times 60{{\left( {\frac{\nu }{{{{\nu }_{D}}}}} \right)}^{3}}{{\left( {1 - \frac{\nu }{{{{\nu }_{D}}}}} \right)}^{2}}.$Изменение формы оптической полосы поглощения при повышении температуры приводит к изменению формы сигнала двухимпульсного эха. Подобное изменение сигнала эха с ростом температуры демонстрирует рис. 4, на котором показан экспериментальный результат для сигнала двухимпульсного некогерентного фотонного эха из работы [18]. При высокой температуре, когда БФЛ фактически пропадает, форма сигнала фотонного эха определяется фононным крылом оптической полосы.
Рис. 4.
Перераспределение вкладов в дефазировку от БФЛ и ФК, происходящее при температурном изменении формы оптической полосы. Взято из [18].

ЗАКЛЮЧЕНИЕ
Уравнения Блоха не могут описать временную эволюцию системы, в которой актуальны электронно-колебательные переходы (см., например рис. 1). Поэтому в 1990 г. автор рассмотрел в работе [15] временную эволюцию электронно-колебательной системы на основе матрицы плотности для такой системы. Результатом этого рассмотрения стала бесконечная система уравнений (3).
В данной статье показано, что с помощью вектора Блоха для электронно-колебательной системы, (обобщенного вектора Блоха) мы можем рассматривать временную эволюцию системы аналогично тому, как это делается при рассмотрении более простых систем, описываемых с помощью оптических уравнений Блоха. Благодаря бесконечному числу компонент в обобщенном векторе Блоха в выражении для дипольного момента излучателя появляются бесконечные суммы, которые описывают собой форму электронно-колебательных полос. Мы показали, что для вычисления этих сумм можно использовать теорию, построенную ранее автором для электронно-колебательных полос, изложенную в работах [21, 22].
Если в уравнениях Блоха релаксация поляризации описывается с помощью времени дефазировки Т2, которое вводится феноменологически, то в нашей более общей теории релаксация поляризации на фемтосекундной и пикосекундной шкале описывается функцией дефазировки $\varphi (t,T),$ и только на более длинной временной шкале эта релаксация описывается константой Т2; причем теория дает микроскопическое выражение (16) для этой, зависящей от температуры константы.
Результат теории, представленной в статье, кратко можно кратко сформулировать следующим образом. Оптическая дефазировка систем с электронно-колебательными переходами определяется шириной бесфононной линии оптической полосы, которая проявляет себя с помощью константы Т2, а также фононным крылом, которое проявляет себя с помощью функции дефазировки $\varphi (t,T).$
Работа выполнена в рамках Государственного задания Института спектроскопии Российской академии наук.
Список литературы
Bloch F. // Phys. Rev. 1946. V. 70. P. 460.
Hahn E.L. // Phys. Rev. 1950. V. 80. P. 580.
Калачев А.А., Самарцев В.В. Когерентные явления в оптике. Казань: Изд-во КГУ, 2003.
Blume R.I. // Bull. Am. Phys. Soc. 1956. V. 1. P. 397.
Даутов Р.А., Корепанов В.Д., Фадеев В.М. // ЖЭТФ. 1959. Т. 37. С. 308.
Maiman N.Y. // Nature. 1960. V. 187. P. 493.
Копвиллем У.Х., Нагибаров В.Р. // ФММ. 1963. Т. 15. С. 313.
Kurnit N.F., Abella I.D., Hartmann S.R. // Phys. Rev. Lett. 1964. V. 13. P. 567.
Копвиллем У.Х., Нагибаров В.Р., Пирожков В.А. и др. // ФТТ. 1972. Т. 14. С. 1794.
Алимпиев С.С., Карлов Н.Н. // ЖЭТФ. 1972. Т. 63. С. 482.
Allen L., Eberly J.H. Optical resonance and two-level atoms. N.Y.–London–Sydney–Toronto: Wiley Intersci. Publ., 1975.
Маныкин Э.А., Самарцев В.В. Оптическая эхо-спектроскопия. М.: Наука, 1984.
Евсеев И.В., Рубцова Н.Н., Самарцев В.В. Когерентные переходные процессы в оптике. М.: Физматлит, 2009.
Персонов Р.И., Осадько И.С., Годяев Э.Д., Аль-шиц Е.И. // ФТТ. 1971. Т. 13. С. 2653.
Осадько И.С. // ЖЭТФ. 1990. Т. 98. С. 1045; Osad’ko I.S. // Sov. Phys. JETP. 1990. V. 71. P. 583.
Козлов С.А., Самарцев В.В. Оптика фемтосекундных лазеров. СПб: Изд-во ИТМО, 2007.
Samartsev V.V., Shegeda A.M., Shkalikov A.V. et al. // Las. Phys. Lett. 2007. V. 4. № 7. P. 534.
Vainer Yu.G., Kol’chenko M.F., Naumov A.V. et al. // J. Chem. Phys. 2002. V. 116. P. 8959.
Каримуллин К.Р., Князев М.В., Наумов А.В. // Изв. РАН. Сер. физ. 2014. Т. 78. № 12. С. 1539; Karimullin K.R., Knyazev M.V., Naumov A.V. // Bull. Russ. Acad. Sci. Phys. 2014. V. 78. № 12. P. 1254.
Knyazev M.V., Karimullin K.R., Naumov A.V. // Phys. Stat. Sol. RRL. 2017. V. 11. № 3. Art. № 1600414.
Осадько И.С. // ЖЭТФ. 1977. Т. 72. С. 1575; Osad’ko I.S. // Sov. Phys. JETP. 1977. V. 45. P. 827.
Осадько И.С. // Селективная спектроскопия одиночных молекул. М.: Физматлит, 2000.
Осадько И.С. Квантовая динамика молекул, взаимодействующих с фотонами, фононами и туннельными системами. М.: Физматлит, 2017.
Осадько И.С., Сташек М.В. // ЖЭТФ. 1994. Т. 106. С. 535; Osad’ko I.S, Stashek M.V. // JETP. 1994. V. 79. P. 293.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая