Известия РАН. Серия физическая, 2019, T. 83, № 3, стр. 306-310

ВВЕДЕНИЕ

На протяжении уже нескольких десятков лет атомные ансамбли, охлажденные в магнито-оптических ловушках, являются объектами повышенного внимания. Такие ансамбли, благодаря своим уникальным физическим свойствам, а также возможности относительно легкого управления их основными параметрами, являются перспективными объектами во многих экспериментах, направленных как на диагностику состояния самого ансамбля, так и на реализацию различных приложений в метрологии, стандартах частоты и квантовой информатике [1–3].

Пробное излучение, рассеявшееся на атомном ансамбле, несет в себе информацию как о внутреннем состоянии атомов, так и об их пространственно-скоростном распределении. В оптически плотных ансамблях важную роль в формировании рассеянного света играет многократное рассеяние и связанные с ним интерференционные процессы. Здесь выделяется эффект когерентного обратного рассеяния (КОР) [4–9], обусловленный интерференцией двух встречных волн, одна из которых формируется в результате последовательного рассеяния света на некоторой цепочке атомов, а другая – на той же цепочке, но при прохождении ее в обратном направлении. Для среды покоящихся двухуровневых атомов разность фаз этих волн зависит от координат первого ${{\vec {r}}_{1}}$ и последнего ${{\vec {r}}_{N}}$ атомов в рассматриваемой цепочке и равна $\Delta \varphi = \left( {\vec {k} + \vec {k}{\text{'}}} \right)\left( {{{{\vec {r}}}_{N}} - {{{\vec {r}}}_{1}}} \right),$ где $\vec {k}$ и $\vec {k}{\text{'}}$ волновые векторы падающей и рассеянной волн соответственно [4]. Для рассеяния вблизи направления, противоположного направлению падающей волны, Δφ ≈ 0, что обеспечивает неисчезающую при усреднении по случайному расположению атомов конструктивную интерференцию, дающую резко анизотропную добавку к угловому распределению интенсивности – конус обратного рассеяния.

Интерференционные эффекты вследствие своей чувствительности к скоростному и пространственному распределению атомов в ансамбле, к их внутренней структуре, которая, в частности, может быть модифицирована внешними вспомогательными полями, могут быть полезны в прецизионных методах диагностики состояния ансамбля.

Влияние внешнего статического электрического или магнитного поля на процесс рассеяния света холодным атомным ансамблем рассматривали в ряде работ. Так, в [10–13] исследовали влияние магнитного поля на эффект КОР в разреженных атомных ансамблях и было показано усиление роли интерференционных процессов при увеличении напряженности поля. В работах [14–17] исследовали влияние внешних полей на рассеяние света ансамблем атомов, концентрация которых такова, что необходимо учитывать зависимое рассеяние.

Некоторые аспекты эффектов, связанных с многократным рассеянием, исследовали недостаточно подробно. В частности, не исследовано влияние внешнего электростатического поля на угловое распределение рассеянного света. В настоящей работе для случая разреженного ансамбля холодных двухуровневых атомов (переход J_g = = 0 → J_e = 1) это влияние проанализировано. Особое внимание обращено на угловую зависимость фактора усиления – величины, характеризующей интерференционные процессы и представляющей собой отношение полной интенсивности рассеянного в данном направлении света к ее неинтерференционной составляющей.

В заключительной части работы обсуждается возможность применения развиваемых подходов в актуальной, но также малоизученной области, связанной с изучением нерезонансного рассеяния в магнитных наножидкостях и совершенных оптических кристаллах.

ДИФФЕРЕНЦИАЛЬНОЕ СЕЧЕНИЕ МНОГОКРАТНОГО РАССЕЯНИЯ

В экспериментах с атомными облаками рассеянный свет регистрируется с помощью фотодетектора, расположенного под нужным углом. Ток фотодетектора в условиях поляризационного анализа выражается через корреляционную функцию электромагнитного поля

где $E_{{\mu }}^{{\left( + \right)}}$ и $E_{{\mu }}^{{\left( - \right)}}$ – положительно- и отрицательно-частотные компоненты гейзенберговского оператора электрического поля, определенные на поверхности фотодетектора. Угловые скобки соответствуют усреднению по оператору плотности всей рассматриваемой системы.

Задавая поляризацию падающего излучения и располагая поляризационный анализатор перед фотодетектором, можно осуществить различные схемы поляризационного анализа рассеянного света. В данной работе рассмотрены четыре основные схемы: $\left. {L\,} \right\|L,$ $L{\kern 1pt} \bot {\kern 1pt} L,$ $\left. {H\,} \right\|H,$ $H{\kern 1pt} \bot {\kern 1pt} H,$ где $L$ соответствует линейной, а H – циркулярной поляризациям. Случаи $\left. {L\,} \right\|L$ и $\left. {H\,} \right\|H$ соответствуют анализу рассеяния без изменения линейной поляризации или спиральности, $L{\kern 1pt} \bot {\kern 1pt} L$ и $H{\kern 1pt} \bot {\kern 1pt} H$ – измерению интенсивности поляризационной компоненты, ортогональной исходной.

В теории для расчета корреляционной функции поля, определяющей ток фотодетектора, мы использовали диаграммную технику Константинова–Переля–Келдыша для неравновесных систем. Как показано в наших предыдущих работах (см. [7–9] и ссылки там же), применение этой техники к подобным задачам позволяет получать явные аналитические выражения для сечений многократного рассеяния. Не вдаваясь в подробности, отметим некоторые ключевые моменты рассматриваемого подхода.

В случае слабого излучения корреляционная функция поля (1) может быть представлена в виде разложения в ряд по числу актов некогерентного рассеяния. В соответствующем диаграммном разложении можно выделить два вклада, основных в нашей задаче. Первый неинтерференционный вклад описывает некогерентное однократное, двукратное и т.д. рассеяние света в оптически плотной среде. Соответствующие диаграммы называются лестничными. Следующий вклад, появляющийся в диаграммном разложении, – интерференционный, начинается с сечения двукратного рассеяния и ответственен за эффект КОР. Этот вклад описывается циклическими или максимально перекрестными диаграммами.

Таким образом, дифференциальное сечение рассеяния можно записать в следующем виде

где верхний индекс N у сечения рассеяния указывает на кратность рассеяния, а второе равенство выделяет неинтерференционный (нижний индекс L) и интерференционный (нижний индекс C) вклады.

Используемый диаграммный подход позволяет записать сечение N-кратного рассеяния как 6N-кратный интеграл по координатам и скоростям всех атомов. В подынтегральное выражение входят следующие величины: одноатомная матрица плотности, характеризующая пространственное и скоростное распределения атомов в ансамбле, а также внутреннее состояние атомов, в котором они были приготовлены; фотонная функция Грина, описывающая распространение света в сплошной среде, с тензором восприимчивости $\chi _{i}^{j}\left( {\vec {r},\omega } \right)$, между актами некогерентного рассеяния; тензор однократного рассеяния $\alpha _{i}^{j}\left( \omega \right).$ Приведем явные выражения для некоторых из перечисленных величин [8, 9]. Тензор рассеяния для рассматриваемого в работе случая имеет следующий вид:

где (d_i)_m0 – матричный элемент дипольного момента перехода $\left| {{{J}_{g}} = 0,{{M}_{g}} = 0} \right\rangle \equiv \left| 0 \right\rangle $ → $\left| {{{J}_{e}} = 1,{{M}_{e}}} \right\rangle \equiv $ $ \equiv \left| m \right\rangle ,$ ω – частота пробного излучения, γ – естественная ширина возбужденного состояния атома, ω_m0 – частота атомного перехода с учетом штарковского сдвига Δ_E.

Фотонная функция Грина пропорциональна медленно меняющейся амплитуде ${\rm X}_{k}^{l}\left( {{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}},\omega } \right).$ В системе координат с осью $\tilde {z}$, сонаправленной с лучом, направление распространения которого определено вектором ${{\vec {r}}_{1}} - {{\vec {r}}_{2}},$ эта амплитуда имеет следующий вид

где интеграл вычисляется вдоль луча, а знак “тильда” над тензором восприимчивости $\tilde {\chi }_{k}^{{j{\text{'}}}}\left( {\vec {r},\omega } \right)$ указывает на его определение в соответствующей системе координат. В лабораторной системе координат с осью z, направленной вдоль внешнего постоянного поля, тензор восприимчивости диагонален где i, j = 0,±1 и ${{\left\| {{{d}_{{{{J}_{e}}{{J}_{g}}}}}} \right\|}^{2}}$ – приведенный матричный элемент дипольного момента атомного перехода. Главные значения тензора различаются только величинами резонансных частот ω_i0, содержащих штарковские сдвиги.

Далее приведены результаты расчетов, выполненных при следующих предположениях. Пространственное распределение атомов является симметричным гауссовым распределением – n(r) = = n₀ exp(–r²/2r₀²), где r₀ – радиус облака, n₀ – концентрация атомов в центре облака. Температура ансамбля считается настолько низкой, что движением атомов в расчетах пренебрегается, но при этом ансамбль не является вырожденным. Атомы в ансамбле приготовлены в основном состоянии $\left| {{{J}_{g}} = 0,{{M}_{g}} = 0} \right\rangle .$

Величину электростатического поля будем характеризовать штарковским сдвигом Δ_E, нормированным на естественную ширину γ. Пробное излучение будет настраиваться точно в резонанс соответствующему переходу. В работе исследуется только некогерентная составляющая рассеянного света, вклад когерентного рассеяния вперед указан не будет.

В качестве основного параметра атомного облака, определяющего характер многократного рассеяния, берется резонансная оптическая толщина $b = \sqrt {2\pi } {{n}_{0}}{{\sigma }_{0}}{{r}_{0}}$ [6, 7], где – сечение резонансного рассеяния на одном атоме и 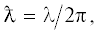где λ – длина волны пробного излучения.

В настоящей работе 3N-кратные интегралы, входящие в сечения N-кратного рассеяния, рассчитывались численно методом Монте-Карло.

РЕЗУЛЬТАТЫ

На рис. 1 представлено угловое распределение интенсивности рассеянного света. Графики на рисунке хорошо демонстрирует отличие двух поляризационных каналов $\left. {H\,} \right\|H$ и $H{\kern 1pt} \bot {\kern 1pt} H$ друг от друга. Это отличие связано с тем, что для канала $\left. {H\,} \right\|H$ вклад однократного рассеяния в полную интенсивность для углов вблизи направления назад практически отсутствует [21] и наоборот – индикатриса однократного рассеяния для канала $H{\kern 1pt} \bot {\kern 1pt} H$ для рассеяния строго назад имеет максимальное значение. Также из рисунка видно, что включение электрического поля влияет на угловое распределение практически для всех углов рассеяния. При этом интенсивность рассеянного света для углов вблизи направления рассеяния вбок увеличивается сильнее, чем для некогерентного рассеяния вперед. Для углов рассеяния вблизи направления назад виден конус обратного рассеяния.

Исследуем более подробно угловую зависимость конуса обратного рассеяния для разных поляризационных каналов и влияние на эту зависимость постоянного электрического поля.

Рисунок 2 демонстрирует пространственную анизотропию фактора усиления, проявляющуюся в каналах с линейной поляризацией. Направление распространения падающего на ансамбль пробного излучения перпендикулярно наведенной оптической оси, а вектор линейной поляризации сонаправлен с ней. Для каждого из двух поляризационных каналов $\left. {L\,} \right\|L,$ $L{\kern 1pt} \bot {\kern 1pt} L$ рассматривается зависимость фактора усиления от угла θ при φ = π и от угла φ при θ = π/2.

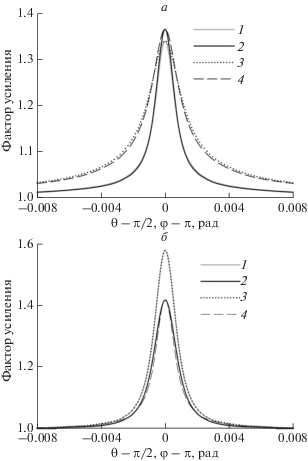
Из графиков видно, что в поляризационном канале $\left. {L\,} \right\|L$ (рис. 2а), включение электрического поля практически не изменяет фактора усиления. Присутствующая анизотропия обусловлена угловой зависимостью сечения однократного рассеяния [18], которое в данном случае практически совпадает с сечением для классического диполя. Основные изменения при включении поля происходят для малых углов вблизи направления назад, где фактор усиления немного возрастает.

Для поляризационного канала $L{\kern 1pt} \bot {\kern 1pt} L$ (рис. 2б) влияние наведенной анизотропии более существенно. В данном случае электрическое поле, изменяя индикатрису однократного рассеяния, приводит к существенному уменьшению фактора усиления.

На следующем рис. 3 построены графики угловой зависимости фактора усиления при разных оптических толщинах ансамбля. Пробное излучение поляризовано циркулярно. Из сравнения графиков на рис. 3а и 3б видно, что величина фактора усиления больше в случае поляризационного канала $\left. {H\,} \right\|H.$ В этом канале фактор усиления может принимать свое максимальное значение, равное двум. Такое отличие между каналами $H{\kern 1pt} \bot {\kern 1pt} H$ и $\left. {H\,} \right\|H$ связано с отсутствием в последнем сильного вклада однократного рассеяния (см. рис. 1). Именно поэтому при увеличении оптической толщины, а следовательно, при повышении роли многократного рассеяния, максимум фактора усиления растет для случая $H{\kern 1pt} \bot {\kern 1pt} H$ и остается постоянным для $\left. {H\,} \right\|H.$ Для малых углов вблизи направления назад важным фактором здесь является и наличие частичного штарковского расщепления, обеспечивающего уменьшение числа каналов, не дающих вклада в интерференционную составляющую.

Рисунок 3 также показывает, что увеличение радиуса облака при постоянной оптической плотности b (при этом должна уменьшается концентрация) приводит к сужению ширины фактора усиления. Это эффект связан с чувствительностью вкладов высоких порядков рассеяния к конечным размерам среды. Оценки показывают [18], что ширина конуса Δθ обратно пропорциональна характерному линейному размеру среды Δθ ~ 1/kr₀. Необходимо отметить, что в работе [18] анализировали конус обратного рассеяния для атомов ⁸⁵Rb, D2-линия, сверхтонкий переход F_g = 3 → F_e = 4, в случае отсутствия внешнего поля. Однако поведение фактора усиления, обнаруженное в этой работе, оказывается сходным с поведением, представленным на рис. 3.

На рис. 3 во избежание нагромождения мы не представали данные для случая Δ_E = 0, но расчеты показывают, что в этом случае будут наблюдаться количественные изменения фактора усиления того же порядка, что и на рис. 2.

ЗАКЛЮЧЕНИЕ

Исследована угловая зависимость света, рассеянного оптически плотным холодным атомным ансамблем, помещенным в постоянное электрическое поле. Основное внимание было уделено угловой зависимости фактора усиления при когерентном обратном рассеянии.

Показано, что электрическое поле, приводя к анизотропии атомного ансамбля, влияет на интерференционные процессы при многократном рассеянии, приводя к изменению амплитуды и/или ширины угловой зависимости фактора усиления.

Мы ограничились исследованием рассеяния света на ансамбле холодных атомов, однако интерференционные процессы, имеющие место при многократном рассеянии, могут быть важны и для других систем. В последнее время усиливается интерес к изучению тонких поляризационных эффектов в зондирующем лазерном излучении, рассеянном в магнитных жидкостях и в совершенных оптических кристаллах [19, 20]. Эффекты многократного рассеяния также могут являться основой хороших диагностических методов, необходимых для понимания процессов, происходящих и в таких системах.

Исследование выполнено за счет гранта Российского научного фонда (проект № 17-12-01085).