Известия РАН. Серия физическая, 2019, T. 83, № 7, стр. 900-903

ВВЕДЕНИЕ

Существование вихревой асимметричной структуры 180° доменной границы (ДГ) Блоха в тонких магнитных пленках типа пермаллоя в области толщин пленки (50–200 нм) впервые было показано в работах [1, 2]. Экспериментальные исследования [3–5] подтвердили, что 180° ДГ Блоха имеют по крайней мере двумерное распределение намагниченности.

В [1] двумерное распределение намагниченности получено численным методом, а в [2] – c использованием аналитических потенциальных функций. Распределения намагниченности в обоих случаях практически совпадают.

В работах [6, 7] рассмотрены аналитические модели, в которых для описания распределения намагниченности в ДГ используются очень сложные функции с большим числом переменных параметров.

В данной работе предлагается метод, который позволяет для распределения намагниченности в двумерной ДГ Блоха, использовать простые аналитические функции с минимально необходимым числом переменных параметров.

АНАЛИТИЧЕСКАЯ МОДЕЛЬ ДВУМЕРНОЙ ДГ БЛОХА

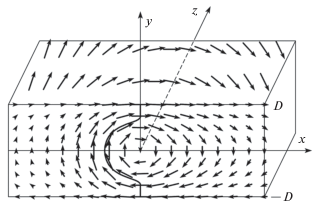
В тонких магнитных пленках домены с противоположной намагниченностью разделяются 180°-ДГ. Рассмотрим пленку толщиной $2{\kern 1pt} D$ с осью легкого намагничивания, параллельной оси $z.$ 180°-ДГ разделяет два домена, намагниченных вдоль оси $ \pm z.$ Распределение намагниченности в ДГ определяется изменением вектора намагниченности $\vec {M}$ = = ${{M}_{S}}\vec {m}$ = ${{M}_{S}}({{m}_{x}}\vec {i} + {{m}_{y}}\vec {j} + {{m}_{z}}\vec {k}),$ ($\vec {M} = {{M}_{S}}$ – намагниченность насыщения пленки). В данной работе рассматриваются двумерные модели, в которых направляющие косинусы ${{m}_{x}}(x,y),$ ${{m}_{y}}(x,y)$ и ${{m}_{z}}(x,y)$ совпадают с осями $x,y$ и $z$ прямоугольной системы координат и зависят от двух переменных $x,y$ и не зависит от переменной $z.$ На рис. 1 показано пространственное распределение намагниченности в вихревой асимметричной доменной границы Блоха.

Для определения направляющих косинусов ${{m}_{x}}(x,y),$ ${{m}_{y}}(x,y)$ и ${{m}_{z}}(x,y)$ вектора намагниченности $\vec {M}$ используется потенциальная функция [2], которую представим в следующем виде:

где согласно [2] используется переменная

и $t$ = ${x \mathord{\left/ {\vphantom {x D}} \right. \kern-0em} D},$ $s$ = ${y \mathord{\left/ {\vphantom {y D}} \right. \kern-0em} D}$ – относительные переменные.

Введя обозначение $q(s)$ = ${{dQ(s)} \mathord{\left/ {\vphantom {{dQ(s)} {ds}}} \right. \kern-0em} {ds}},$ направляющие косинусы можно определить следующими выражениями:

В области ДГ существует линия перехода ${{t}_{0}}(s),$ вдоль которой по толщине пленки происходит изменение направления намагниченности на противоположное. Линия перехода находится из совместного решения уравнений (4):

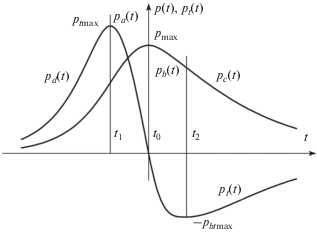
При построении аналитической модели изменение функции $p(t)$ для всей области $ - \infty < t < \infty $ (рис. 2) разбивается на четыре области: область ${{t}_{1}} \leqslant t \leqslant {{t}_{0}},$ в которой изменение $p(t) = {{p}_{a}}(t);$ область ${{t}_{0}} \leqslant t \leqslant {{t}_{2}},$ в которой изменение $p(t) = {{p}_{b}}(t);$ область ${{t}_{2}} \leqslant t < \infty ,$ в которой изменение $p(t) = {{p}_{c}}(t)$ и область $ - \infty < t < {{t}_{1}},$ в которой изменение p(t) = = p_d(t).

В области ${{t}_{1}} \leqslant t \leqslant {{t}_{0}}$ изменение $p(t)$ происходит монотонным образом от максимального значения ${{p}_{{max}}}$ при $t = {{t}_{0}}$ до некоторого значения ${{p}_{a}}$ = = $p(t = {{t}_{1}})$ (рис. 2), а изменение производной ${{p}_{t}}(t)$ происходит от ${{p}_{t}}(t = {{t}_{0}}) = 0$ до максимального значения ${{p}_{t}}(t = {{t}_{1}})$ = ${{p}_{{t\,max}}}$ (рис. 2).

Для создания асимметрии в двумерной ДГ Блоха в смежной области ${{t}_{0}} \leqslant t \leqslant {{t}_{2}}$ используется зависимость ${{p}_{b}}(t),$ изменение которой происходит от максимального значения ${{p}_{{max}}}$ при $t = {{t}_{0}}$ до некоторого значения ${{p}_{b}}$ = ${{p}_{b}}(t = {{t}_{2}})$ (рис. 2), а изменение производной ${{d{{b}_{b}}(t)} \mathord{\left/ {\vphantom {{d{{b}_{b}}(t)} {dt}}} \right. \kern-0em} {dt}}$ =${{p}_{{bt}}}(t)$ происходит от значения ${{p}_{{bt}}}(t = {{t}_{0}})$ = 0 до минимального значения ${{p}_{{bt}}}(t = {{t}_{2}})$ = $ - {{p}_{{bt\,max}}}$ (рис. 2). Функция ${\kern 1pt} {{p}_{b}}(t)$ имеет следующий вид:

где a₀ = π/2/t₂ и b₀ = π/t₂. Неизвестные коэффициенты (${{a}_{1}},$ ${{b}_{1}},$ ${{c}_{1}},$ ${{d}_{1}}$) в (5) находим из условий непрерывности для $t = {{t}_{0}}{\text{:}}$

и из условий непрерывности для $t = {{t}_{2}}{\text{:}}$ 1) p_bt(t = t₂) = = –p_{btt max}; 2) p_bt(t = t₂) = 0.

Изменение функции ${\kern 1pt} {{p}_{b}}(t)$ зависит от двух независимых параметров: параметр ${\kern 1pt} {{t}_{2}}$ задает координату, для которой второй параметр принимает минимальное значение $ - {{p}_{{bt\,max}}}.$ Параметр ${{p}_{{bt\,max}}}$ определяет асимметрию в двумерной ДГ Блоха при ${{p}_{{bt\,max}}}$ < ${{p}_{{t\,max}}}.$

Для области $\left( {{{t}_{2}} \leqslant t < \infty } \right)$ с использованием функции $\varphi (ct)$ = $2{\text{arctg}}(\exp (ct))$ – ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ [8] изменение функции ${\kern 1pt} {{p}_{c}}(t)$ принимаем в следующем виде:

Параметры ${{C}_{0}},$ ${\kern 1pt} c$ и ${\kern 1pt} {{t}_{c}}$ в (6) определяем из условий непрерывности на границе $t = {{t}_{2}}{\text{:}}$

Из совместного решения этих уравнений получим: ${{C}_{0}} = \sqrt 2 {{p}_{b}},$ $c = {{\sqrt 2 {{p}_{{bt\,max}}}} \mathord{\left/ {\vphantom {{\sqrt 2 {{p}_{{bt\,max}}}} {{{p}_{b}}}}} \right. \kern-0em} {{{p}_{b}}}}$ и t_c = t₂ – $ - \ln tg{{({{3\pi } \mathord{\left/ {\vphantom {{3\pi } {8)}}} \right. \kern-0em} {8)}}} \mathord{\left/ {\vphantom {{({{3\pi } \mathord{\left/ {\vphantom {{3\pi } {8)}}} \right. \kern-0em} {8)}}} {c.}}} \right. \kern-0em} {c.}}$

Для области ${\kern 1pt} - \infty < t < {{t}_{1}}$ изменение функции ${\kern 1pt} {{p}_{d}}(t)$ примем в следующем виде:

Параметры ${{D}_{0}},$ ${\kern 1pt} d$ и ${\kern 1pt} {{t}_{d}}$ в (7) определяем из условий непрерывности на границе $t = {{t}_{1}}{\text{:}}$

Из решения этих уравнений получим: D₀ = = $\sqrt 2 {{p}_{a}},$ $d = {{\sqrt 2 {{p}_{{t\,max}}}} \mathord{\left/ {\vphantom {{\sqrt 2 {{p}_{{t\,max}}}} {{{p}_{a}}}}} \right. \kern-0em} {{{p}_{a}}}}$ и ${{t}_{d}}$ = ${{{{t}_{1}} - \ln tg({\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0em} 8})} \mathord{\left/ {\vphantom {{{{t}_{1}} - \ln tg({\pi \mathord{\left/ {\vphantom {\pi 8}} \right. \kern-0em} 8})} d}} \right. \kern-0em} d}.$

Для определения неизвестной четной функции $g(s)$ и ее производной ${{g}_{s}}(s)$ в области линии перехода ${{t}_{1}} \leqslant t \leqslant {{t}_{0}}$ найдем опорные значения этих функций из условия существования линии перегиба (4a) для $q(s) = 0{\text{:}}$

Для середины пленки $s = 0$ производная ${\kern 1pt} {{g}_{s}}(s = 0) = 0$ и при $t = {{t}_{1}}$ (см. рис. 2) согласно (8) ${{\left( {{{p}_{t}}({{t}_{0}}(s = 0)g(s = 0)} \right)}^{2}}$ = ${{\left( {{{p}_{t}}(t = {{t}_{1}}){{g}_{0}}} \right)}^{2}}$ = ${{\left( {{{p}_{{t\,max}}}{{g}_{0}}} \right)}^{2}} = 1$ получаем максимальное значение $g(s = 0)$ = = ${{g}_{0}} = {1 \mathord{\left/ {\vphantom {1 {{{p}_{{t\,max}}}}}} \right. \kern-0em} {{{p}_{{t\,max}}}}}.$ Для дополнительных приповерхностных областях ${{s}_{1}} \leqslant |s| \leqslant 1$ для $q(s) = 0$ полагаем, что линия перегиба ${{t}_{0}}(s) = {{t}_{0}},$ и согласно (8) для $s = \pm {{s}_{1}}$ получаем $g(s = \pm {{s}_{1}})$ = ${{g}_{p}}$ и ${{g}_{s}}(s = \pm {{s}_{1}})$ = $ \mp {{g}_{{s1}}}$ = ${{ \mp 1} \mathord{\left/ {\vphantom {{ \mp 1} {{{p}_{{max}}}}}} \right. \kern-0em} {{{p}_{{max}}}}}.$

Для определения функции $g(s)$ в качестве исходной функции для области $ - {{s}_{1}} \leqslant s \leqslant {{s}_{1}}$ используется выражение для третьей производной в следующем виде: ${{g}_{{sss}}}(s)$ = ${{a}_{1}}\sin ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} {{{s}_{1}}}}} \right. \kern-0em} {{{s}_{1}}}}).$ Выражение $g(s)$ для области $ - {{s}_{1}} \leqslant s \leqslant {{s}_{1}}$ имеет следующий вид:

Для дополнительной области ${{s}_{1}} \leqslant s \leqslant 1$ изменение функции $g(s)$ происходит по линейной зависимости:

На поверхности пленки $s = 1$ выражение (10) принимает вид: $g(s = 1)$ = ${{g}_{1}}$ = ${{g}_{p}} - {{g}_{{s1}}}(1 - {{s}_{1}}),$ где ${{g}_{1}}$ характеризует выход намагниченности на поверхностях пленки, значение которого определяет магнитостатическую энергию ДГ. Выражение (10) с учетом ${{g}_{1}}$ представим так: ${{g}_{p}}$ = ${{g}_{1}} + {{g}_{{s1}}}(1 - {{s}_{1}}),$ и подставляя в (9) для $s = 0,$ получим значение

где ${{g}_{{01}}}$ = ${{({{g}_{0}} - {{g}_{1}})} \mathord{\left/ {\vphantom {{({{g}_{0}} - {{g}_{1}})} {{{g}_{{s1}}}}}} \right. \kern-0em} {{{g}_{{s1}}}}}.$

Из решения системы уравнений (4) методом Ньютона находим зависимости для линии перегиба ${{t}_{0}}(s)$ и $q(s)$ для области $ - {{s}_{1}} \leqslant s \leqslant {{s}_{1}},$ где в качестве начальных значений используются ${\kern 1pt} t(s = 0) = {{t}_{1}}$ и $q(s = 0) = 0.$ Для дополнительных областей ${{s}_{1}} \leqslant \left| s \right| \leqslant 1$ линия перегиба: ${\kern 1pt} {{t}_{0}}(s) = {{t}_{0}}$ и $q(s) = 0.$

РЕЗУЛЬТАТЫ РАСЧЕТА

Равновесное состояние ДГ определяется минимумом полной энергии

где ${{E}_{A}}$ – обменная энергия, ${\kern 1pt} {{E}_{K}}$ – энергия анизотропии и ${\kern 1pt} {{E}_{S}}$ – магнитостатическая энергия. Для сравнения с результатами, полученными другими авторами, в данной работе используются относительные значения полной энергии $\omega = {E \mathord{\left/ {\vphantom {E A}} \right. \kern-0em} A}$ и ее составляющих ${{\omega }_{A}} = {{{{E}_{A}}} \mathord{\left/ {\vphantom {{{{E}_{A}}} A}} \right. \kern-0em} A},$ ${{\omega }_{K}} = {{{{E}_{K}}} \mathord{\left/ {\vphantom {{{{E}_{K}}} A}} \right. \kern-0em} A}$ и ${{\omega }_{S}} = {{{{E}_{S}}} \mathord{\left/ {\vphantom {{{{E}_{S}}} A}} \right. \kern-0em} A}.$ Вычисления были выполнены для тонкой магнитной пленки типа пермаллоя толщиной $2{\kern 1pt} D$ = 100 нм со значениями обменной константы $A = {{10}^{{ - 6}}}$ эрг ∙ см^–1, константы анизотропии $K = {{10}^{3}}$ эрг ∙ см^–3 и намагниченности насыщения ${{M}_{S}}$ = 800 Гс. Для численного вычисления полной энергии и ее составляющих толщина пленки делится на ${{N}_{x}} \times {{N}_{y}}$ квадратных призм. Ширина призмы $\Delta = {{2D} \mathord{\left/ {\vphantom {{2D} {{{N}_{y}}}}} \right. \kern-0em} {{{N}_{y}}}}$ = 1.25 нм. Непрерывное распределение намагниченности в каждой призме заменяется дискретным, причем каждая призма намагничена однородно. Направление дискретной намагниченности то же самое, что и направление, определяемое непрерывным распределением в центре призмы.

Для расчета в области линии перехода используем следующую зависимость

Зависимость (12) при ${{p}_{{max}}} = 1$ определяется двумя независимыми параметрами: ${{t}_{1}} = {{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \mathord{\left/ {\vphantom {{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} a}} \right. \kern-0em} a}$ и ${{p}_{{t\,max}}}.$ Для рассматриваемой модели двумерной ДГ Блоха получено минимальное значение полной энергии ДГ $\omega $ = 21.46, обменной энергии ${{\omega }_{A}}$ = 21.13, энергии анизотропии ${{\omega }_{K}}$ = 0.06 и магнитостатической энергии ${{\omega }_{S}}$ = 0.27. Структура двумерной ДГ Блоха соответствует следующим значениям переменных параметров: ${{t}_{0}} = 0,$ ${{t}_{2}} = - {{t}_{1}}$ = 0.459, ${{p}_{{t\,max}}}$ = ${{{{p}_{{bt\,max}}}} \mathord{\left/ {\vphantom {{{{p}_{{bt\,max}}}} 2}} \right. \kern-0em} 2}$ = 1.18, ${{g}_{1}}$ = 0.064 и ${{s}_{1}}$ = 0.727. На рис. 1 показано распределение намагниченности в двумерной ДГ Блоха.

Полная энергия ДГ Блоха, полученная для данной модели, имеет самое низкое значение по сравнению с полной энергией для аналитических моделей в [2, 6, 7], но выше полной энергии в [1], распределение намагниченности в которой получено численным методом: $\omega $ = 19.55, ${{\omega }_{A}}$ = 18.49, ${{\omega }_{K}}$ = 0.06 и ${{\omega }_{S}}$ = 1.00.

ЗАКЛЮЧЕНИЕ

На основе решения системы уравнений для линии перехода предложен аналитический метод определения распределения намагниченности в двумерной ДГ Блоха. Для описания двумерного распределения были использованы простые аналитические зависимости, содержащие минимальное число переменных параметров, которые задают изменение намагниченности по ширине ДГ: два параметра в области линии перехода и два параметра в асимметричной области.