Известия РАН. Серия физическая, 2019, T. 83, № 9, стр. 1174-1178
Особенности фазового перехода в тонком сегнетоэластическом стержне
В. Н. Нечаев 1, А. В. Шуба 1, *
1 Федеральное государственное казенное военное образовательное учреждение высшего образования
Военный учебно-научный центр Военно-воздушных сил “Военно-воздушная академия
имени профессора Н.Е. Жуковского и Ю.А. Гагарина”
Воронеж, Россия
* E-mail: shandvit@rambler.ru
Поступила в редакцию 12.11.2018
После доработки 29.03.2019
Принята к публикации 27.05.2019
Аннотация
В рамках феноменологической теории фазовых переходов второго рода Ландау показано, что в тонком сегнетоэластическом стержне возможен фазовый переход в неоднородную доменоподобную фазу. Определен волновой вектор неоднородной структуры, и установлены условия ее существования в зависимости от геометрических размеров сегнетоэластического стержня, его упругих свойств и свойств поверхности.
В тех случаях, когда фазовый переход (ФП) в материале сопровождается возникновением дальнодействующих полей (электрических, магнитных, упругих), при определенных условиях возможно образование неоднородных “доменоподобных” состояний. В работе [1] было показано, что ФП на поверхности полуограниченного образца происходит в пространственно-модулированное неоднородное состояние с волновым вектором, зависящим от свойств материала в объеме и на поверхности. Позже автором работ [2, 3] было отмечено, что подобная ситуация также может наблюдаться в полуограниченном сегнетоэластике или сегнетоэластической пластине. В работе [4] путем численного решения нелинейной задачи установлено, что аналогичный случай имеет место для нанокомпозитных материалов с сегнетоэлектрическими выделениями. Далее в работе [5] численно-аналитическим методом было показано, что в тонкой сегнетоэлектрической пленке возможен ФП в пространственно-модулированное неоднородное состояние. Здесь отличие неоднородных “доменоподобных” состояний от классических доменов состоит в отсутствии четких границ между полярными областями, в поведении этой структуры во внешнем поле и в достаточно жестких условиях ее возникновения.
В настоящей работе численно-аналитическим путем устанавливается, что в тонком сегнетоэластическом стержне так же, как и в сегнетоэлектрической пленке [5], при определенных условиях возможен ФП в неоднородное “доменоподобное” состояние. Отметим, что в данной работе речь идет о неоднородности вдоль оси стержня, в отличие от неоднородности по его сечению, присутствующей всегда в наноразмерных образцах. Цель настоящей работы – установление температурной области существования неоднородных состояний при ФП второго рода как функции геометрических размеров сегнетоэластического стержня прямоугольного сечения с учетом свойств его поверхности. Поставленную задачу в линейном приближении оказывается возможным решить аналитически, и только итоговые формулы проанализировать численными методами. Покажем это.
Рассмотрим модель однодоменного сегнетоэластика в виде тонкого монокристаллического стержня прямоугольного сечения ${{l}_{1}} \times {{l}_{2}},$ расположенного параллельно оси 0z. Свободную энергию такого стержня запишем в виде [6]:
(1)
$\begin{gathered} F = \frac{1}{V}\int\limits_V {\left[ { - \frac{\alpha }{{\text{2}}}{{\eta }^{2}} + \frac{\beta }{{\text{4}}}{{\eta }^{4}} + \frac{\kappa }{{\text{2}}}{{{\left( {\nabla \eta } \right)}}^{2}} - \sigma _{{xy}}^{{\left( e \right)}}\eta } \right]} dV + \\ + \,\,\frac{1}{S}\int\limits_S {\frac{{{{\alpha }_{s}}}}{{\text{2}}}{{\eta }^{2}}dS} , \\ \end{gathered} $и граничное условие к нему
(3)
${{\left. {\frac{{{{\alpha }_{s}}\eta }}{\kappa } + \frac{{d\eta }}{{d\vec {n}}}} \right|}_{S}} = 0,$Уравнение (2) необходимо решать совместно с уравнениями упругого равновесия
(4)
$\frac{{\partial \sigma _{{ij}}^{{\left( e \right)}}}}{{\partial {{x}_{j}}}} = 0,\,\,\,\,i,j = 1,2.$Используя закон Гука [7], выражаем напряжения $\sigma _{{ij}}^{{\left( e \right)}}$ через упругие деформации $u_{{kl}}^{{\left( e \right)}}{\text{:}}$
где тензор упругих модулей ${{\lambda }_{{ijkl}}}$ в изотропном случае имеет вид:(6)
${{\lambda }_{{ijkl}}} = \lambda {{\delta }_{{ij}}}{{\delta }_{{kl}}} + \mu \left( {{{\delta }_{{ik}}}{{\delta }_{{jl}}} + {{\delta }_{{il}}}{{\delta }_{{jk}}}} \right),$в котором λ, μ – коэффициенты Ламе, δij – символ Кронекера. Далее вектор перемещений $\vec {u}\left( {{{u}_{x}},{{u}_{y}}} \right)$ разбиваем на сумму упругой ${{\vec {u}}^{{\left( e \right)}}}$ и пластической ${{\vec {u}}^{{\left( p \right)}}}$ составляющих. Тогда подстановка выражения (5) с учетом равенства (6) в уравнения упругого равновесия (4) дает уравнения
(7)
$\left( {\lambda {{\delta }_{{ij}}}{{\delta }_{{kl}}} + \mu \left( {{{\delta }_{{ik}}}{{\delta }_{{jl}}} + {{\delta }_{{il}}}{{\delta }_{{jk}}}} \right)} \right)\left( {\frac{{{{\partial }^{2}}{{u}_{k}}}}{{\partial {{x}_{l}}\partial {{x}_{j}}}} - \frac{{{{\partial }^{2}}u_{k}^{{\left( p \right)}}}}{{\partial {{x}_{l}}\partial {{x}_{j}}}}} \right) = 0,$а напряжения $\sigma _{{xy}}^{{\left( e \right)}}$ в уравнениях равновесия (2), (4) с учетом выражения
(8)
$u_{{ij}}^{{\left( p \right)}} = \left\{ \begin{gathered} \eta ,\,\,\,\,i \ne j, \hfill \\ 0,\,\,\,i = j \hfill \\ \end{gathered} \right.$перепишутся в виде
(9)
$\sigma _{{xy}}^{{\left( e \right)}} = \mu \left( {\frac{{\partial {{u}_{x}}}}{{\partial y}} + \frac{{\partial {{u}_{y}}}}{{\partial x}}} \right) - 2\mu \eta .$После упрощений уравнения (7) с учетом выражения (8) примут вид
(10)
$\begin{gathered} \Delta {{u}_{i}} + \frac{1}{{1 - 2\nu }}{{\nabla }_{i}}{\text{div}}\vec {u} - 2{{\delta }_{{i1}}}\frac{{\partial \eta }}{{\partial y}} - 2{{\delta }_{{i2}}}\frac{{\partial \eta }}{{\partial x}} = 0, \\ i = 1,2, \\ \end{gathered} $Неизвестные функции ux, uy, η будем искать в виде
(11)
$\begin{gathered} \eta \left( {x,y,z} \right) = \eta \left( {x,y} \right){{e}^{{iqz}}}{\text{;}} \hfill \\ {{u}_{x}}\left( {x,y,z} \right) = {{u}_{x}}\left( {x,y} \right){{e}^{{iqz}}}{\text{;}} \hfill \\ {{u}_{y}}\left( {x,y,z} \right) = {{u}_{y}}\left( {x,y} \right){{e}^{{iqz}}}, \hfill \\ \end{gathered} $(12)
$\left\{ \begin{gathered} \kappa \left( {\frac{{{{\partial }^{2}}\eta }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\eta }}{{\partial {{y}^{2}}}}} \right)\, + \,\left( {\alpha - 2\mu - {{q}^{2}}\kappa } \right){\kern 1pt} \eta + \mu \left( {\frac{{\partial {{u}_{x}}}}{{\partial y}} + \frac{{\partial {{u}_{y}}}}{{\partial x}}} \right) = 0, \hfill \\ \frac{{2 - 2\nu }}{{1 - 2\nu }}\frac{{{{\partial }^{2}}{{u}_{x}}}}{{\partial {{x}^{2}}}} - {{q}^{2}}{{u}_{x}}\, + \frac{{{{\partial }^{2}}{{u}_{x}}}}{{\partial {{y}^{2}}}} + \hfill \\ + \,\,\frac{1}{{1 - 2\nu }}\frac{{{{\partial }^{2}}{{u}_{y}}}}{{\partial x\partial y}} - 2\frac{{\partial \eta }}{{\partial y}} = 0, \hfill \\ \frac{{2 - 2\nu }}{{1 - 2\nu }}\frac{{{{\partial }^{2}}{{u}_{y}}}}{{\partial {{y}^{2}}}} - {{q}^{2}}{{u}_{y}}\, + \frac{{{{\partial }^{2}}{{u}_{y}}}}{{\partial {{x}^{2}}}} + \frac{1}{{1 - 2\nu }}\frac{{{{\partial }^{2}}{{u}_{x}}}}{{\partial x\partial y}} - 2\frac{{\partial \eta }}{{\partial x}} = 0. \hfill \\ \end{gathered} \right.$Решение для функции $\eta \left( {x,y} \right)$ удобно искать в виде разложения по собственным функциям задачи Штурма–Лиувилля для прямоугольной области:
(13)
$\Delta \eta + \xi \eta = 0;\,\,\,\,{{\left. {\frac{{{{\alpha }_{s}}\eta }}{\kappa } + \frac{{d\eta }}{{d\vec {n}}}} \right|}_{S}} = 0,$(14)
$\begin{gathered} \eta \left( {x,y} \right) = \\ = \sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {{{a}_{{nm}}}} } \left( {\frac{\kappa }{{{{\alpha }_{s}}}}\sqrt {{{\upsilon }_{n}}} \cos \left( {\sqrt {{{\upsilon }_{n}}} x} \right) + \sin \left( {\sqrt {{{\upsilon }_{n}}} x} \right)} \right) \times \\ \times \,\,\left( {\frac{\kappa }{{{{\alpha }_{s}}}}\sqrt {{{\psi }_{m}}} \cos \left( {\sqrt {{{\psi }_{m}}} y} \right) + \sin \left( {\sqrt {{{\psi }_{m}}} y} \right)} \right), \\ {{\xi }_{{nm}}} = {{\upsilon }_{n}} + {{\psi }_{m}},\,\,\,\,n,m \in {\rm N}, \\ \end{gathered} $(15)
${\text{tg}}\left( {\sqrt {{{\upsilon }_{n}}} {{l}_{1}}} \right) = \frac{{2\sqrt {{{\upsilon }_{n}}} {{\alpha }_{s}}\kappa }}{{{{\upsilon }_{n}}{{\kappa }^{2}} - \alpha _{s}^{2}}};\,\,\,\,{\text{tg}}\left( {\sqrt {{{\psi }_{m}}} {{l}_{2}}} \right) = \frac{{2\sqrt {{{\psi }_{m}}} {{\alpha }_{s}}\kappa }}{{{{\psi }_{m}}{{\kappa }^{2}} - \alpha _{s}^{2}}}.$Функции ${{u}_{x}}\left( {x,y} \right)$ и ${{u}_{y}}\left( {x,y} \right)$ согласно формуле (14) удобно искать в виде
(16)
$\begin{gathered} {{u}_{x}}\left( {x,y} \right) = \sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {{{b}_{{nm}}}} } \left( {\frac{\kappa }{{{{\alpha }_{s}}}}\sqrt {{{\upsilon }_{n}}} \cos \left( {\sqrt {{{\upsilon }_{n}}} x} \right)} \right. + \\ + \left. {_{{_{{_{{_{{}}}}}}}}^{{^{{^{{^{{}}}}}}}}\sin \left( {\sqrt {{{\upsilon }_{n}}} x} \right)} \right)\left( {\frac{\kappa }{{{{\alpha }_{s}}}}\sqrt {{{\psi }_{m}}} \sin \left( {\sqrt {{{\psi }_{m}}} y} \right) - \cos \left( {\sqrt {{{\psi }_{m}}} y} \right)} \right), \\ {{u}_{y}}\left( {x,y} \right) = \sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {{{c}_{{nm}}}} } \left( {\frac{\kappa }{{{{\alpha }_{s}}}}\sqrt {{{\upsilon }_{n}}} \sin \left( {\sqrt {{{\upsilon }_{n}}} x} \right) - } \right. \\ - \left. {_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}^{{^{{^{{}}}}}}\cos \left( {\sqrt {{{\upsilon }_{n}}} x} \right)} \right)\left( {\frac{\kappa }{{{{\alpha }_{s}}}}\sqrt {{{\psi }_{m}}} \cos \left( {\sqrt {{{\psi }_{m}}} y} \right) + \sin \left( {\sqrt {{{\psi }_{m}}} y} \right)} \right), \\ \end{gathered} $(17)
$\left\{ \begin{gathered} \left[ {\kappa \left( {{{\upsilon }_{n}} + {{\psi }_{m}}} \right) - \alpha + 2\mu + {{q}^{2}}\kappa } \right]{{a}_{{nm}}} - \mu \sqrt {{{\psi }_{m}}} {{b}_{{nm}}} - \mu \sqrt {{{\upsilon }_{n}}} {{c}_{{nm}}} = 0, \hfill \\ 2\sqrt {{{\psi }_{m}}} {{a}_{{nm}}} - \left[ {\frac{{2 - 2\nu }}{{1 - 2\nu }}{{\upsilon }_{n}} + {{\psi }_{m}} + {{q}^{2}}} \right]{{b}_{{nm}}} - \frac{1}{{1 - 2\nu }}\sqrt {{{\upsilon }_{n}}{{\psi }_{m}}} {{c}_{{nm}}} = 0, \hfill \\ 2\sqrt {{{\upsilon }_{n}}} {{a}_{{nm}}} - \frac{1}{{1 - 2\nu }}\sqrt {{{\upsilon }_{n}}{{\psi }_{m}}} {{b}_{{nm}}} - \left[ {\frac{{2 - 2\nu }}{{1 - 2\nu }}{{\psi }_{m}} + {{\upsilon }_{n}} + {{q}^{2}}} \right]{{c}_{{nm}}} = 0. \hfill \\ \end{gathered} \right.$Однородная система линейных уравнений (17) будет иметь нетривиальные решения только в том случае, когда еe определитель равен нулю:
(18)
$\begin{gathered} \kappa \left( {{{\upsilon }_{n}} + {{\psi }_{m}}} \right) - {{\alpha }_{0}}\left( {{{T}_{C}} - T} \right) + 2\mu + {{q}^{2}}\kappa - 2\mu \times \\ \times \,\,\frac{{\frac{{2 - 2\nu }}{{1 - 2\nu }}\left( {\upsilon _{n}^{2} + \psi _{m}^{2}} \right) + {{q}^{2}}\left( {{{\upsilon }_{n}} + {{\psi }_{m}}} \right) - \frac{{4\nu }}{{1 - 2\nu }}{{\upsilon }_{n}}{{\psi }_{m}}}}{{\frac{{2 - 2\nu }}{{1 - 2\nu }}{{{\left( {{{\upsilon }_{n}} + {{\psi }_{m}}} \right)}}^{2}} + \frac{{3 - 4\nu }}{{1 - 2\nu }}{{q}^{2}} + {{q}^{4}}}} = 0. \\ \end{gathered} $По свойству собственных значений, с увеличением индексов n, m величины ${{\upsilon }_{n}},$ ${{\psi }_{m}}$ возрастают. Поэтому минимальная температура Tr, при которой появляется отличное от нуля решение, соответствующее минимальному ненулевому собственному значению ${{\xi }_{{11}}} = {{\upsilon }_{1}} + {{\psi }_{1}},$ будет являться температурой ФП:
(19)
$\begin{gathered} {{T}_{r}} = {{T}_{C}}\left[ {1 - \frac{\kappa }{{{{\alpha }_{0}}{{T}_{C}}}}\left( {{{\upsilon }_{1}} + {{\psi }_{1}} + {{q}^{2}}} \right) - \frac{{2{{\mu }^{{^{{}}}}}}}{{{{\alpha }_{0}}{{T}_{C}}}}} \right. \times \\ \times \,\,\left. {\frac{{4{{\upsilon }_{1}}{{\psi }_{1}} + \left( {1 - 2\nu } \right)\left( {{{\upsilon }_{1}} + {{\psi }_{1}} + {{q}^{2}}} \right){{q}^{2}}}}{{\left( {2 - 2\nu } \right){{{\left( {{{\upsilon }_{1}} + {{\psi }_{1}}} \right)}}^{2}} + \left( {3 - 4\nu } \right)\left( {{{\upsilon }_{1}} + {{\psi }_{1}}} \right){{q}^{2}} + \left( {1 - 2\nu } \right){{q}^{4}}}}} \right]. \\ \end{gathered} $Для иллюстрации полученных результатов следует использовать параметры сегнетоэластических кристаллов с фазовым переходом второго рода, к которым относятся литиево-цезиевый сульфат LiCsSO4, ванадат висмута BiVO4, тригидроселенит калия KH3(SeO3)2 и др. Поведение температуры Tr будем рассматривать на примере модельного сегнетоэластика KH3(SeO3)2 с параметрами: TC = 211 К, κ = 10–7 Н, α0 = 90.9 ∙ 106 Н ∙ м2 ∙ К–1, λ = 36 ГПа; μ = = 5.05 ГПа, межатомное расстояние $a \approx 3$ Å [9]. На рис. 1 представлены зависимости температуры Tr ФП сегнетоэластического стержня от нормированного волнового вектора $\tilde {q} = qa$ для разных приведенных размеров ${{\tilde {l}}_{1}} = {{{{l}_{1}}} \mathord{\left/ {\vphantom {{{{l}_{1}}} a}} \right. \kern-0em} a}$ квадратного сечения с нормированным параметром ${{\tilde {\alpha }}_{s}} = {{\alpha }_{s}}{a \mathord{\left/ {\vphantom {a \kappa }} \right. \kern-0em} \kappa }$ на его границе.
Рис. 1.
Зависимость температуры Tr фазового перехода от волнового вектора $\tilde {q}$ для квадратного сечения стержня с размерами ${{\tilde {l}}_{1}}{\text{:}}$ 1 – 60, 2 – 70, 3 – 80, 4 – 90, 5 – 100, 6 – 110 $\left( {{{{\tilde {\alpha }}}_{s}} = 1} \right).$
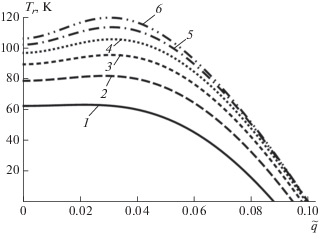
Как видно из рис. 1, при малых размерах сечения l1 ≤ 60a ФП осуществляется однородно по всему объему стержня, т.к. функции ${{T}_{r}}\left( {\tilde {q}} \right)$ монотонно убывают, начиная с минимального значения $\tilde {q} = 0.$ Для размеров l1 > 60a происходит ФП в пространственно-модулированное неоднородное состояние с ненулевым волновым вектором $\tilde {q}{\text{*,}}$ зависящим от размера l1 стержня и величины αs закрепления параметра порядка на поверхности S. При этом реальная температура ${{T}_{{rh}}}$ ФП и волновой вектор $\tilde {q}{\text{*}}$ статической волны, возникающей при ФП, соответствуют точке максимума ${{T}_{{rh}}} = T_{r}^{{\left( {\max } \right)}}$ на зависимости ${{T}_{r}}\left( {\tilde {q}} \right)$ (рис. 1). Такая ситуация наблюдается и в случае различного закрепления параметра порядка на границе образца (рис. 2), и в случае изменения формы сечения (рис. 3).
Рис. 2.
Зависимость температуры Tr фазового перехода от волнового вектора $\tilde {q}$ для сегнетоэластического стержня квадратного сечения размером ${{l}_{1}} = 50a$ с параметрами ${{\tilde {\alpha }}_{s}}{\text{:}}$ 1 – 0.2, 2 – 0.1, 3 – 0.05, 4 – 0.025, 5 – 0.0125.
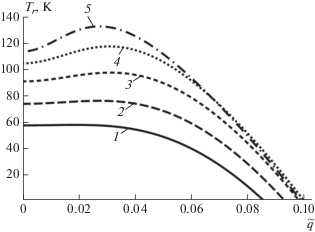
Рис. 3.
Зависимость температуры Tr фазового перехода от волнового вектора $\tilde {q}$ при изменении соотношения сторон сечения стержня ${{{{l}_{1}}} \mathord{\left/ {\vphantom {{{{l}_{1}}} {{{l}_{2}}}}} \right. \kern-0em} {{{l}_{2}}}}{\text{:}}$ 1 – 0.6, 2 – 0.7, 3 – 0.8, 4 – 0.9, 5 – 1, 6 – 1.1 $\left( {{{l}_{2}} = 100a} \right).$
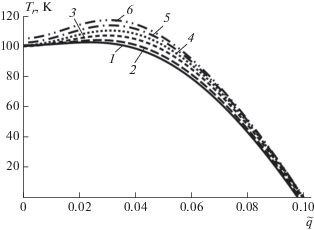
На рис. 3 представлены результаты влияния формы сечения стержня на особенности ФП в нем. Наблюдается увеличение температуры ФП с ростом соотношения ${{{{l}_{1}}} \mathord{\left/ {\vphantom {{{{l}_{1}}} {{{l}_{2}}}}} \right. \kern-0em} {{{l}_{2}}}}.$ Однако повышение температуры ФП с возрастанием длины ${{\tilde {l}}_{1}}$ прямоугольного сечения (рис. 3) слабее, чем в случае одновременного увеличения размеров ${{\tilde {l}}_{1}} = {{\tilde {l}}_{2}}$ квадратного сечения стержня (рис. 1) по причине меньшего приращения энергии упорядочения для прямоугольного сечения.
С увеличением размера сечения температура ${{T}_{{rh}}} = T_{r}^{{\left( {\max } \right)}}$ ФП, отвечающая максимальному значению на кривой ${{T}_{r}}\left( {\tilde {q}} \right),$ возрастает (рис. 4), и область существования неоднородного состояния ${\Delta }T = {{T}_{r}}\left( {\tilde {q}{\text{*}}} \right) - {{T}_{r}}\left( 0 \right)$ расширяется (рис. 5). С уменьшением параметра ${{\tilde {\alpha }}_{s}}$ температура Trh ФП в неоднородное состояние растет (рис. 2, 4) в связи со снижением вклада энергии поверхности в свободную энергию (1). Возрастание функции ${{T}_{{rh}}}\left( {{{{\tilde {l}}}_{1}}} \right)$ объясняется уменьшением корреляционной и поверхностной составляющих по сравнению с другими вкладами в свободную энергию (1). Снижение температуры Trh с повышением параметра ${{\tilde {\alpha }}_{s}}$ естественно связать с увеличением вклада поверхностной энергии. Заметим, что поведение функции ${{T}_{{rh}}}\left( {{{{\tilde {l}}}_{1}}} \right)$ по сути аналогично зависимости температуры ФП в однородное состояние от размера сечения стержня [8].
Рис. 4.
Зависимость температуры Trhфазового перехода в неоднородное состояние от размера ${{\tilde {l}}_{1}}$ c параметрами ${{\tilde {\alpha }}_{s}}{\text{:}}$ 1 – 0.1, 2 – 0.2, 3 – 0.4, 4 – 0.8, 5 – 1.6, 6 – 3.2.

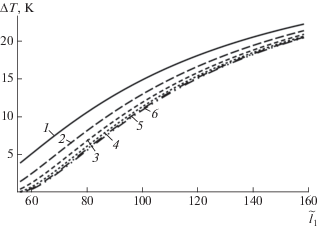
Рис. 5.
Зависимость ширины температурного интервала $\Delta T$ существования неоднородной фазы от размера ${{\tilde {l}}_{1}}$ сечения стержня c параметрами ${{\tilde {\alpha }}_{s}}{\text{:}}$ 1 – 0.1, 2 – 0.2, 3 – 0.4, 4 – 0.8, 5 – 1.6, 6 – 3.2.
Таким образом, использованное линейное приближение позволяет вычислить температуру $T_{r}^{{\left( {\max } \right)}}$ ФП и период статической волны спонтанной деформации, определяемый волновым вектором $q*,$ как функции параметров материала. Дальнейшая температурная эволюция этих состояний может быть исследована только при условии выхода за рамки линейного приближения.
Отметим отличие рассмотренной ситуации с сегнетоэластиком от аналогичных задач для сегнетоэлектриков и ферромагнетиков. В последних двух случаях ФП в конечном образце обязательно сопровождается возникновением деполяризующих или размагничивающих полей и, следовательно, всегда имеются предпосылки к образованию неоднородных структур, если будут выполняться другие необходимые условия [5]. В сегнетоэластических образцах упругие поля при ФП возникают только при определенной их геометрии, согласованной с пластической деформацией, сопровождающей ФП, то есть, когда отличен от нуля тензор несовместности пластических деформаций [10]. Другими словами, условия для наблюдения неоднородных “доменоподобных” структур в сегнетоэластиках являются более жесткими.
Список литературы
Андреев А.Ф. // Письма в ЖЭТФ. 1980. Т. 32. № 11. С. 654.
Лавриненко Н.М. // ФНТ. 1996. Т. 22. № 10. С. 1132.
Лавриненко Н.М. // ФНТ. 1997. Т. 23. № 8. С. 880.
Нечаев В.Н., Висковатых А.В. // ФТТ. 2015. Т. 57. № 4. С. 704; Nechaev V.N., Viskovatykh A.V. // Phys. Sol. St. 2015. V. 57. № 4. P. 722.
Нечаев В.Н., Шуба А.В. // ФТТ. 2018. Т. 60. № 7. С. 1322; Nechaev V.N., Shuba A.V. // Phys. Sol. St. 2018. V. 60. № 7. P. 1332.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 8. Электродинамика сплошных сред. М.: Физматлит, 2005. 656 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 7. Теория упругости. М.: Физматлит, 2003. 264 с.
Nechaev V.N., Shuba A.V. // Ferroelectrics. 2016. V. 501. P. 32.
Гриднев С.А., Кудряш В.И., Шувалов Л.А. // Изв. АН СССР. Сер. физ. 1979. Т. 43. № 8. С. 1718.
Кренер Э. Общая континуальная теория дислокаций и собственных напряжений. М.: Мир, 1965. 104 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


