Известия РАН. Серия физическая, 2020, T. 84, № 1, стр. 61-66
Влияние сильной электромагнитной волны на проводимость β-Ga2O3
В. Л. Абдрахманов 1, Д. В. Завьялов 1, В. И. Конченков 1, *, С. В. Крючков 1, 2
1 Федеральное государственное бюджетное учреждение высшего образования
“Волгоградский государственный технический университет”
Волгоград, Россия
2 Федеральное государственное бюджетное учреждение высшего образования
“Волгоградский государственный социально-педагогический университет”
Волгоград, Россия
* E-mail: kontchenkov@yandex.ru
Поступила в редакцию 29.07.2019
После доработки 30.08.2019
Принята к публикации 27.09.2019
Аннотация
На основе анализа квантового кинетического уравнения, учитывающего рассеяние электронов на заряженных примесях, исследуется проводимость оксида галлия при воздействии на образец сильной электромагнитной волны и постоянного электрического поля, векторы напряженности которых сонаправлены. Показано, что при температуре порядка 100 К основной вклад в проводимость вносят процессы упругого рассеяния, а процессы с поглощением и испусканием фотонов становятся существенными лишь при значениях амплитуды напряженности волны порядка 106 В ∙ см–1.
Оксид галлия в последние несколько лет активно исследуется как экспериментально, так и теоретически, что связано с развитием технологии получения этого материала и широкими перспективами его использования в области силовой электроники и в качестве основы для твердотельных излучателей света в ультрафиолетовом диапазоне [1‒5]. Рассматриваемый материал вплоть до значений энергий носителей тока в зоне проводимости порядка нескольких электрон-вольт имеет параболический закон дисперсии, эффективная масса носителей заряда составляет $m = 0.28\,{{т}_{e}}$ (${{т}_{e}}$ – масса свободного электрона). Анализ экспериментов по исследованию эффекта Холла [4], проведенный в работе [6], показывает, что при комнатных температурах основным механизмом, обеспечивающим проводимость β-модификации оксида галлия, является рассеяние на полярных оптических фононах, а при температурах порядка 100 К – рассеяние на заряженных примесях [7]. В серии работ, посвященных квантовохимическому моделированию электронной структуры и подвижности носителей тока в оксиде галлия [8–11], также подтверждается этот вывод. В работе [12] из первых принципов исследуется подвижность носителей заряда в оксиде галлия, отмечается преобладающий вклад в подвижность рассеяния на полярных оптических фононах, указывается на снижение подвижности при высоких концентрациях носителей тока.
Создание источников и детекторов излучения, работающих в ультрафиолетовом диапазоне,
требует исследования высокочастотных свойств материала, причем следует рассматривать
волну, частота $\Omega $ которой велика по сравнению со средней частотой столкновений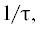 
т.е. $\Omega \tau \gg 1$ ($\tau $ – время релаксации импульса электрона). Такая ситуация соответствует области применимости
квантового кинетического уравнения [13, 14]. В настоящей работе предпринята попытка решить квантовое кинетическое уравнение
для электронного газа с параболическим законом дисперсии, когда вдоль одной из осей
(для определенности – вдоль оси Z) приложены постоянное электрическое поле напряженностью ${{E}_{1}}$ и высокочастотное переменное электрическое поле сильной волны c напряженностью ${{E}_{0}}\sin \Omega t.$ При этом основным механизмом рассеяния предполагается рассеяние на примесях. Напряженность
постоянного электрического поля выбирается равной порядка ${{10}^{4}}{\text{--}}{{10}^{5}}$ В ∙ см–1 – при таких значениях, как показывают расчеты [10, 15], вольт-амперная характеристика оксида галлия соответствует закону Ома, а энергетический
спектр можно считать параболическим.
Квантовое кинетическое уравнение получено в [13] для электрон-фононной системы, однако формально можно учесть взаимодействие электронов с заряженными примесями, считая такие столкновения упругими. Для невырожденного электронного газа в предположении, что фононный газ является равновесным, квантовое кинетическое уравнение принимает вид (1).
(1)
$\begin{gathered} \frac{{\partial {{f}_{{\vec {p}}}}}}{{\partial t}} + e{{{\vec {E}}}_{1}}\frac{{\partial {{f}_{{\vec {p}}}}}}{{\partial{ \vec {p}}}} = - \frac{{2\pi }}{\hbar }\operatorname{Re} \sum\limits_{\vec {k}} {{{{\left| {{{C}_{{\vec {k}}}}} \right|}}^{2}}} \times \\ \times \,\,\sum\limits_{s,l} {{{J}_{s}}\left( {\frac{{e{{{\vec {E}}}_{0}}}}{{m\hbar {{\Omega }^{2}}}} \cdot \vec {k}} \right)} {{J}_{l}}\left( {\frac{{e{{{\vec {E}}}_{0}}}}{{m\hbar {{\Omega }^{2}}}} \cdot \vec {k}} \right) \times \\ \times \,\,\exp \left[ {i\left( {l - s} \right)t} \right]\int\limits_{ - \infty }^t {dt{\kern 1pt} '} \left\{ {\left[ {{{f}_{{\vec {p}}}}\left( {t{\kern 1pt} '} \right){{N}_{{\vec {k}}}} - } \right.} \right. \\ \left. { - \,\,{{f}_{{\vec {p} + \vec {k}}}}\left( {{{N}_{{\vec {k}}}} + 1} \right)} \right]\exp \left( {\frac{i}{\hbar }\left( {{{\varepsilon }_{{\vec {p} + \vec {k}}}} - {{\varepsilon }_{{\vec {p}}}} - } \right.} \right. \\ \left. {\left. { - \,\,\hbar {{\omega }_{0}} - l\hbar \Omega } \right)\left( {t - t{\kern 1pt} '} \right)} \right) + \left[ {{{f}_{{\vec {p}}}}\left( {t{\kern 1pt} '} \right)\left( {{{N}_{{\vec {k}}}} + 1} \right) - {{f}_{{\vec {p} + \vec {k}}}}{{N}_{{\vec {k}}}}} \right] \times \\ \times \,\,\exp \left( {\frac{i}{\hbar }\left( {{{\varepsilon }_{{\vec {p} + \vec {k}}}} - {{\varepsilon }_{{\vec {p}}}} + \hbar {{\omega }_{0}} - l\hbar \Omega } \right)\left( {t - t{\kern 1pt} '} \right)} \right) - \\ - \,\,\left[ {{{f}_{{\vec {p} - \vec {k}}}}\left( {t{\kern 1pt} '} \right){{N}_{{\vec {k}}}} - {{f}_{{\vec {p}}}}\left( {{{N}_{{\vec {k}}}} + 1} \right)} \right] \times \\ \times \,\,\exp \left( {\frac{i}{\hbar }\left( {{{\varepsilon }_{{\vec {p}}}} - {{\varepsilon }_{{\vec {p} - \vec {k}}}} - \hbar {{\omega }_{0}} - l\hbar \Omega } \right)\left( {t - t{\kern 1pt} '} \right)} \right) - \\ - \,\,\left[ {{{f}_{{\vec {p} - \vec {k}}}}\left( {t{\kern 1pt} '} \right)\left( {{{N}_{{\vec {k}}}} + 1} \right) - {{f}_{{\vec {p}}}}{{N}_{{\vec {k}}}}} \right] \times \\ \left. { \times \,\,\exp \left( {\frac{i}{\hbar }\left( {{{\varepsilon }_{{\vec {p}}}} - {{\varepsilon }_{{\vec {p} - \vec {k}}}} + \hbar {{\omega }_{0}} - l\hbar \Omega } \right)\left( {t - t{\kern 1pt} '} \right)} \right)} \right\}. \\ \end{gathered} $Приведенное уравнение является нелокальным по времени, то есть скорость изменения функции распределения ${{f}_{{\vec {p}}}}$ в текущий момент времени $t$ зависит от значений этой функции во все предыдущие моменты времени. Поскольку целью настоящей работы является вычисление статической проводимости образца оксида галлия, интерес представляет низкочастотная часть функции распределения [13, 14]. Усредняя (1) по промежутку времени $T \gg {{\Omega }^{{ - 1}}},$ $\hbar \varepsilon _{{\vec {p}}}^{{ - 1}}$ и считая ${{f}_{{\vec {p}}}}$ медленно меняющейся по сравнению с экспонентами в правой части (1), получаем уравнение для низкочастотной составляющей электронной функции распределения:
(2)
$\begin{gathered} e{{{\vec {E}}}_{1}}\frac{{\partial {{f}_{{\vec {p}}}}}}{{\partial{ \vec {p}}}} = \frac{{2\pi }}{\hbar }{{\sum\limits_{\vec {k}} {\left| {{{C}_{{\vec {k}}}}} \right|} }^{2}}\sum\limits_{l = - \infty }^\infty {J_{l}^{2}\left( {\frac{{e{{{\vec {E}}}_{0}}}}{{m\hbar {{\Omega }^{2}}}} \cdot \vec {k}} \right)} \times \\ \times \,\,\left\{ {\left[ {{{f}_{{\vec {p} + \vec {k}}}}\left( {{{N}_{{\vec {k}}}} + 1} \right) - {{f}_{{\vec {p}}}}{{N}_{{\vec {k}}}}} \right]} \right. \times \\ \times \,\,\delta \left( {{{\varepsilon }_{{\vec {p} + \vec {k}}}} - {{\varepsilon }_{{\vec {p}}}} - l\hbar \Omega - \hbar {{\omega }_{{\vec {k}}}}} \right) + \\ + \,\,\left[ {{{f}_{{\vec {p} - \vec {k}}}}{{N}_{{\vec {k}}}} - {{f}_{{\vec {p}}}}\left( {{{N}_{{\vec {k}}}} + 1} \right)} \right] \times \\ \times \,\,\left. {\delta \left( {{{\varepsilon }_{{\vec {p} - \vec {k}}}} - {{\varepsilon }_{{\vec {p}}}} - l\hbar \Omega + \hbar {{\omega }_{{\vec {k}}}}} \right)} \right\}. \\ \end{gathered} $С учетом упругости рассеяния $\left( {{{\omega }_{{ - \vec {k}}}} = {{\omega }_{{\vec {k}}}} = 0} \right)$ уравнение (2) преобразуется к виду:
(3)
$\begin{gathered} e{{{\vec {E}}}_{1}}\frac{{\partial {{f}_{{\vec {p}}}}}}{{\partial{ \vec {p}}}} = \frac{{2\pi }}{\hbar }{{\sum\limits_{\vec {k}} {\left| {{{C}_{{\vec {k}}}}} \right|} }^{2}}\left( {2{{N}_{{\vec {k}}}} + 1} \right) \times \\ \times \,\,\sum\limits_{l = - \infty }^\infty {J_{l}^{2}\left( {\frac{{e{{{\vec {E}}}_{0}}}}{{m\hbar {{\Omega }^{2}}}} \cdot \vec {k}} \right)} \left[ {{{f}_{{\vec {p} + \vec {k}}}} - {{f}_{{\vec {p}}}}} \right] \times \\ \times \,\,\delta \left( {{{\varepsilon }_{{\vec {p} + \vec {k}}}} - {{\varepsilon }_{{\vec {p}}}} - l\hbar \Omega } \right). \\ \end{gathered} $Для рассмотрения рассеяния на примесях необходимо в (3) сделать замену
(4)
$\begin{gathered} {{\left| {{{С}_{{\vec {k}}}}} \right|}^{2}}\left( {2{{N}_{{\vec {k}}}} + 1} \right) \to \frac{{{{n}_{{ci}}}}}{V}{{\left( {\frac{{4\pi Z{{e}^{2}}}}{{{{\varepsilon }_{{st}}}}}} \right)}^{2}} \times \\ \times \,\,\frac{1}{{{{{\left( {{{{{k}^{2}}} \mathord{\left/ {\vphantom {{{{k}^{2}}} {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}} + {{\eta }^{2}}} \right)}}^{2}}}} = \frac{{{{n}_{{ci}}}}}{V}{{\left( {\frac{{4\pi Z{{e}^{2}}}}{{{{\varepsilon }_{{st}}}}}} \right)}^{2}}\frac{{{{\hbar }^{4}}}}{{{{{\left( {{{k}^{2}} + {{\eta }^{2}}{{\hbar }^{2}}} \right)}}^{2}}}}, \\ \end{gathered} $(5)
$\begin{gathered} e{{{\vec {E}}}_{1}}\frac{{\partial {{f}_{{\vec {p}}}}}}{{\partial{ \vec {p}}}} = \\ = \sum\limits_{\vec {p}'} {\left( {\sum\limits_{l = - \infty }^\infty {J_{l}^{2}\left( {\frac{{e{{{\vec {E}}}_{0}}}}{{m\hbar {{\Omega }^{2}}}} \cdot \left( {\vec {p}{\kern 1pt} ' - \vec {p}} \right)} \right)\frac{{2\pi {{n}_{{ci}}} \cdot {{{\left( {4\pi Z{{e}^{2}}} \right)}}^{2}}{{\hbar }^{3}}}}{{V\varepsilon _{{st}}^{2}{{{\left( {{{{\left( {\vec {p} - \vec {p}'} \right)}}^{2}} + {{\eta }^{2}}{{\hbar }^{2}}} \right)}}^{2}}}}\delta \left( {{{\varepsilon }_{{\vec {p}{\kern 1pt} '}}} - {{\varepsilon }_{{\vec {p}}}} - l\hbar \Omega } \right)} } \right)} \times \\ \times \,\,\left[ {{{f}_{{\vec {p}{\kern 1pt} '}}} - {{f}_{{\vec {p}}}}} \right]. \\ \end{gathered} $Выражение (5) формально можно переписать в виде, соответствующем кинетическому уравнению Больцмана:
(6)
$\begin{gathered} e{{{\vec {E}}}_{1}}\frac{{\partial {{f}_{{\vec {p}}}}}}{{\partial{ \vec {p}}}} = \\ = \sum\limits_{\vec {p}{\kern 1pt} '} {\left\{ {\left( {\sum\limits_{l = - \infty }^\infty {{{W}_{l}}\left( {\vec {p}{\kern 1pt} ',\vec {p}} \right)} } \right){{f}_{{\vec {p}{\kern 1pt} '}}} - \left( {\sum\limits_{l = - \infty }^\infty {{{W}_{l}}\left( {\vec {p},\vec {p}{\kern 1pt} '} \right)} } \right){{f}_{{\vec {p}}}}} \right\}} , \\ \end{gathered} $(7)
$\begin{gathered} {{W}_{l}}\left( {\vec {p},\vec {p}{\kern 1pt} '} \right) = {{W}_{l}}\left( {\vec {p}{\kern 1pt} ',\vec {p}} \right) = J_{l}^{2}\left( {\frac{{e{{{\vec {E}}}_{0}}}}{{m\hbar {{\Omega }^{2}}}} \cdot \left( {\vec {p}{\kern 1pt} ' - \vec {p}} \right)} \right) \times \\ \times \,\,\frac{{2\pi {{n}_{{ci}}} \cdot {{{\left( {4\pi Z{{e}^{2}}} \right)}}^{2}}{{\hbar }^{3}}}}{{\varepsilon _{{st}}^{2}V{{{\left( {{{{\left( {\vec {p}{\kern 1pt} ' - \vec {p}} \right)}}^{2}} + {{\eta }^{2}}{{\hbar }^{2}}} \right)}}^{2}}}}\delta \left( {{{\varepsilon }_{{\vec {p}{\kern 1pt} '}}} - {{\varepsilon }_{{\vec {p}}}} - l\hbar \Omega } \right). \\ \end{gathered} $Величины ${{W}_{l}}\left( {\vec {p},\vec {p}{\kern 1pt} '} \right)$ формально можно рассматривать как вероятности перехода электрона из состояния с квазиимпульсом $\vec {p}$ в состояние с квазиимпульсом $\vec {p}{\kern 1pt} '$ в результате рассеяния на примеси и поглощения или испускания $l$ фотонов с энергией $\hbar \Omega .$ Уравнение вида (6) можно решать численно методом Монте-Карло, полагая ${{W}_{l}}\left( {\vec {p},\vec {p}{\kern 1pt} '} \right)$ равной вероятности рассеяния электрона на $l$-м канале рассеяния. Тогда следует вычислить полную вероятность рассеяния электрона с квазиимпульсом $\vec {p}$ на $l$-ом типе рассеяния ${{W}_{l}}\left( {\vec {p}} \right)$ = $\int {{{W}_{l}}\left( {\vec {p},\vec {p}{\kern 1pt} '} \right)d\vec {p}{\kern 1pt} '} .$ Перейдем в сферическую систему координат, так что ось Z сонаправлена с вектором ${{\vec {E}}_{0}},$ тогда векторы $\vec {p}$ и $\vec {p}{\kern 1pt} '$ характеризуются наборами $\left\{ {p{\kern 1pt} ',\theta ,\varphi } \right\}$ и $\left\{ {p,\alpha ,\beta } \right\}$ соответственно.
(8)
$\begin{gathered} {{W}_{l}}\left( {\vec {p}} \right) = V\int\limits_0^\infty {\frac{{{{p}^{{'2}}}dp{\kern 1pt} '}}{{{{{\left( {2\pi \hbar } \right)}}^{3}}}}} \int\limits_0^\pi {\sin \theta d\theta } \times \\ \times \,\,\int\limits_{ - \pi }^\pi {d\varphi J_{l}^{2}} \left( {\frac{{e{{E}_{0}}}}{{m\hbar {{\Omega }^{2}}}}p{\kern 1pt} '\cos \theta - \frac{{e{{E}_{0}}}}{{m\hbar {{\Omega }^{2}}}} \cdot p\cos \alpha } \right) \times \\ \times \,\,\frac{{2\pi {{n}_{{ci}}} \cdot {{{\left( {4\pi Z{{e}^{2}}} \right)}}^{2}}{{\hbar }^{3}}}}{{\varepsilon _{{st}}^{2}V{{{\left( {p{{'}^{2}} + {{p}^{2}} - 2pp{\kern 1pt} '\cos \left( {{{{\vec {p}}}^{ \wedge }}\vec {p}{\kern 1pt} '} \right) + {{\eta }^{2}}{{\hbar }^{2}}} \right)}}^{2}}}} \times \\ \times \,\,\delta \left( {{{\varepsilon }_{{\vec {p}{\kern 1pt} '}}} - {{\varepsilon }_{{\vec {p}}}} - l\hbar \Omega } \right). \\ \end{gathered} $(9)
$\cos {{\vec {p}}^{ \wedge }}\vec {p}{\kern 1pt} ' = \cos \theta \cos \alpha + \sin \theta \sin \alpha \cos \left( {\varphi - \beta } \right).$Переходим к безразмерным переменным:
(10)
$\begin{gathered} \vec {p} \to \frac{{\vec {p}}}{{\sqrt {2mkT} }},\,\,\,\,\Omega \to \frac{{\hbar \Omega }}{{kT}},\,\,\,\,{{\eta }^{2}} \to \frac{{{{\eta }^{2}}{{\hbar }^{2}}}}{{2mkT}}, \\ {{{\vec {E}}}_{0}} \to \frac{{e{{{\vec {E}}}_{0}}\sqrt {2mkT} }}{{m\hbar {{\Omega }^{2}}}}. \\ \end{gathered} $После взятия интегралов по модулю конечного квазиимпульса электрона $p{\kern 1pt} '$ и по полярному углу $\varphi $ выражение для полной вероятности принимает вид:
(11)
$\begin{gathered} {{W}_{l}}\left( {\vec {p}} \right) = \frac{{8\pi m{{n}_{{ci}}}{{{\left( {Z{{e}^{2}}} \right)}}^{2}}}}{{\varepsilon _{{st}}^{2}{{{\left( {2mkT} \right)}}^{{3/2}}}}}\sqrt {{{p}^{2}} + l\Omega } \,\, \times \\ \times \,\,\int\limits_{ - 1}^1 {dx} J_{l}^{2}\left( {{{E}_{0}}\left( {\sqrt {{{p}^{2}} + l\Omega } x - p\cos \alpha } \right)} \right) \times \\ \times \,\,\left( {{{x}^{2}} \cdot 4{{p}^{2}}\left( {{{p}^{2}} + l\Omega } \right) - x \cdot 4p\left( {2{{p}^{2}} + l\Omega + {{\eta }^{2}}} \right)} \right. \times \\ \times \,\,\sqrt {{{p}^{2}} + l\Omega } \cos \alpha + {{\left( {2{{p}^{2}} + l\Omega + {{\eta }^{2}}} \right)}^{2}} - \\ - \,\,{{\left. {4{{p}^{2}}\left( {{{p}^{2}} + l\Omega } \right){{{\sin }}^{2}}\alpha } \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $Выражение для вероятности рассеяния (11) содержит зависимость от концентрации заряженных примесей и радиуса экранирования. Ширина запрещенной зоны в энергетическом спектре оксида галлия составляет 4.8 эВ, поэтому собственных носителей заряда при комнатных температурах практически нет, и проводимость этого материала определяется примесями. В образцах оксида галлия, исследованных экспериментально в [4], концентрация доноров ${{N}_{D}} = 1.43 \cdot {{10}^{{17}}}$ см–3, концентрация акцепторов ${{N}_{A}} = 4.2 \cdot {{10}^{{16}}}$ см–3, энергия активации донора ${{E}_{D}} = - 28.5$ мэВ (энергия отсчитывается от дна зоны проводимости). Для компенсированного полупроводника концентрация свободных носителей тока $n$ определяется выражением [16]:
(12)
$\frac{{{{N}_{D}}}}{{1 + \frac{{{{h}_{i}}}}{{{{g}_{i}}}}\exp \left( {\frac{{{{E}_{F}} - {{E}_{D}}}}{{kT}}} \right)}} = n + {{N}_{A}},$(13)
${{E}_{F}} = kT\ln \frac{n}{{{{N}_{c}}}},\,\,\,\,{{N}_{C}} = 2{{\left( {\frac{{2\pi mkT}}{{{{{\left( {2\pi \hbar } \right)}}^{2}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}},$${{N}_{C}}$ – эффективная плотность состояний в зоне проводимости [16]. Подставляя (12) в (10), получаем выражение для концентрации свободных носителей заряда:
(14)
$\begin{gathered} n = \frac{{{{N}_{A}} + {{n}_{1}}}}{2}\left( {\sqrt {1 + \frac{{4{{n}_{1}}\left( {{{N}_{D}} - {{N}_{A}}} \right)}}{{{{{\left( {{{N}_{A}} + {{n}_{1}}} \right)}}^{2}}}}} - 1} \right), \\ {{n}_{1}} = \frac{{{{g}_{i}}}}{{{{h}_{i}}}}{{N}_{C}}\exp \left( {\frac{{{{E}_{D}}}}{{kT}}} \right). \\ \end{gathered} $При температуре $T = 100$ К концентрация свободных носителей составляет $n = 4 \cdot {{10}^{{16}}}$ см–3. Концентрация ионизированных примесей определяется выражением [16]:
Обратный квадрат радиуса экранирования
(16)
$\frac{1}{{r_{0}^{2}}} = \frac{{4\pi {{e}^{2}}}}{{{{\varepsilon }_{{st}}}kT}}\left( {n + \frac{{\left( {{{N}_{D}} - {{N}_{A}} - n} \right)\left( {{{N}_{A}} + n} \right)}}{{{{N}_{D}}}}} \right).$При температуре $T = 100$ К значение ${1 \mathord{\left/ {\vphantom {1 {r_{0}^{2}}}} \right. \kern-0em} {r_{0}^{2}}}$ составляет $1.4 \cdot {{10}^{{12}}}$ см–2.
Расчет показывает, что при температуре около 100 K вероятности переходов электрона ${{W}_{l}}\left( {\vec {p}} \right)$ с поглощением и испускания фотонов (то есть для случаев $\left| l \right| > 0$) при амплитуде напряженности электромагнитной волны вплоть до ${{E}_{0}}\sim {{10}^{5}}$ В ∙ см–1 пренебрежимо малы по сравнению с вероятностью ${{W}_{0}}\left( {\vec {p}} \right),$ то есть влияние электромагнитной волны на проводимость оксида галлия определяются упругими процессами. Технически это связано с достаточно большой эффективной массой носителей тока – формально полагая эффективную массу на порядок меньше, получаем вероятности рассеяния с поглощением и испусканием фотона сравнимыми с ${{W}_{0}}\left( {\vec {p}} \right).$ Выражение для вероятности рассеяния имеет вид:
(17)
$\begin{gathered} {{W}_{0}}\left( p \right) = \frac{{8\pi m{{n}_{{ci}}}{{{\left( {Z{{e}^{2}}} \right)}}^{2}}}}{{{{{\left( {2mkT} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\varepsilon _{{st}}^{2}}}p \times \\ \times \,\,\int\limits_{ - 1}^1 {dx\frac{{J_{0}^{2}\left( {{{E}_{0}}px - {{E}_{0}}p\cos \alpha } \right)}}{{{{{\left[ {{{{\left( {2{{p}^{2}} + {{\eta }^{2}}} \right)}}^{2}} - 4{{p}^{2}}\left( {2{{p}^{2}} + {{\eta }^{2}}} \right)x\cos \alpha + 2{{p}^{4}}\left( {2{{x}^{2}} - 1 + \cos 2\alpha } \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \cdot \\ \end{gathered} $На рис. 1 приведен график зависимости ${{W}_{0}}\left( {\vec {p}} \right)$ для случая $\alpha = 0,$ ${{E}_{0}} = {{10}^{4}}$ В ∙ см–1, $\Omega = {{10}^{{14}}}$ c–1. С ростом амплитуды напряженности волны становятся существенными вероятности ${{W}_{1}}\left( {\vec {p}} \right)$ и ${{W}_{{ - 1}}}\left( {\vec {p}} \right),$ соответствующие поглощению и испусканию фотона. На рис. 2 приведены графики вероятностей рассеяния, построенные для значения ${{E}_{0}} = {{10}^{6}}$ В ∙ см–1.
Рис. 1.
Зависимость вероятности ${{W}_{0}}$ рассеяния электрона на заряженных примесях от модуля квазиимпульса электрона $p$ (${{E}_{0}} = {{10}^{4}}$ В ∙ см–1, $\Omega = {{10}^{{14}}}$ c–1, $\alpha = 0$).
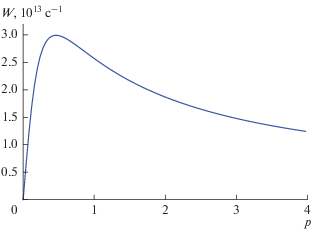
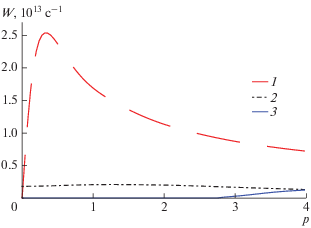
Рис. 2.
Зависимость вероятностей ${{W}_{l}}$ рассеяния электрона на заряженных примесях от модуля квазиимпульса электрона $p$ (${{E}_{0}} = {{10}^{6}}$ В ∙ см–1, $\Omega = {{10}^{{14}}}$ c–1, $\alpha = 0$). 1 – ${{W}_{0}}\left( {\vec {p}} \right),$ вероятность рассеяния без поглощения и испускания фотона; 2 – ${{W}_{1}}\left( {\vec {p}} \right),$ вероятность рассеяния с поглощением фотона; 3 – ${{W}_{{ - 1}}}\left( {\vec {p}} \right),$ вероятность рассеяния с испусканием фотона.
Поскольку в случае воздействия на образец электромагнитной волны с амплитудой напряженности ${{E}_{0}} < {{10}^{5}}$ В ∙ см–1, существенными оказываются упругие процессы электронного рассеяния, можно стандартным образом ввести время релаксации импульсов $\tau .$ Считаем, что добавка к равновесной функции распределения пропорциональна напряженности постоянного электрического поля, которое полагаем слабым в том смысле, что это поле не искажает энергетический спектр материала:
(18)
$f\left( {\vec {p}} \right) = {{f}_{0}}\left( {\vec {p}} \right) + {{f}_{1}}\left( {\vec {p}} \right) = {{f}_{0}}\left( {\vec {p}} \right) + A\left( {{{{\vec {E}}}_{1}},\vec {p}} \right).$В этом случае интеграл столкновений может быть записан в виде $J = {{ - {{f}_{1}}\left( {\vec {p}} \right)} \mathord{\left/ {\vphantom {{ - {{f}_{1}}\left( {\vec {p}} \right)} {\tau \left( {p,\alpha } \right)}}} \right. \kern-0em} {\tau \left( {p,\alpha } \right)}}.$ Средняя частота столкновений определяется выражением:
(19)
$\frac{1}{{\tau \left( {p,\alpha } \right)}} = - \frac{{8{{n}_{{ci}}}{{{\left( {Z{{e}^{2}}} \right)}}^{2}}m}}{{\varepsilon _{{st}}^{2}{{{\left( {2mkT} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}p \cdot J\left( {p,\alpha } \right),$(20)
$\begin{gathered} J\left( {p,\alpha } \right) = \int\limits_0^2 {dz} \int\limits_0^{\pi } d \gamma \times \\ \times \,\,\frac{{J_{0}^{2}\left( {{{E}_{0}}p\cos \alpha \left( { - z + \sqrt {2z - {{z}^{2}}} \operatorname{tg} \alpha \cos \gamma } \right)} \right)}}{{{{{\left( {2{{p}^{2}}z + {{\eta }^{2}}} \right)}}^{2}}}} \times \\ \times \,\,\left( {\left( { - z + \sqrt {2z - {{z}^{2}}} \operatorname{tg} \alpha \cos \gamma } \right)} \right). \\ \end{gathered} $В пределе ${{E}_{0}} \to 0$ (19) переходит в известное выражение для вероятности рассеяния носителей тока на заряженных примесях [19 ] :
(21)
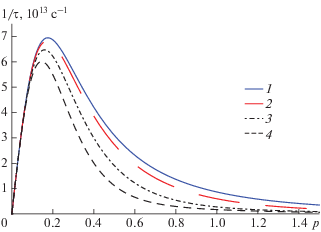
$\begin{gathered} \frac{1}{{\tau \left( p \right)}} = \frac{{\pi \cdot {{n}_{{ci}}} \cdot {{{\left( {Z{{e}^{2}}} \right)}}^{2}}}}{{\varepsilon _{{st}}^{2}\sqrt {2m} {{\varepsilon }_{{\vec {p}}}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}\left( {\ln \left( {1 + x} \right) - \frac{x}{{1 + x}}} \right), \\ x = \frac{{8mr_{0}^{2}{{\varepsilon }_{{\vec {p}}}}}}{{{{\hbar }^{2}}}}. \\ \end{gathered} $Выражение (21) записано в размерных единицах. На рис. 3 приведены графики зависимости ${{\tau }^{{ - 1}}}\left( p \right),$ усредненные по углу рассеяния $\alpha ,$ построенные для разных значений амплитуды напряженности ${{E}_{0}}$ высокочастотного электрического поля. Видно, что средняя частота столкновений слабо зависит от ${{E}_{0}}$ вплоть до значений ${{E}_{0}}\sim {{10}^{6}}$ В ∙ см–1. Усредненное по модулю квазиимпульса электрона значение времени релаксации импульса $\tau \sim {{10}^{{ - 13}}}$ c, таким образом, при $\Omega = {{10}^{{14}}}$ c–1 исходное предположение $\Omega \tau \gg 1,$ при котором справедливо уравнение для низкочастотной части функции распределения (2), выполняется.
Рис. 3.
Зависимость средней частоты столкновений $1{\text{/}}\tau $ от модуля квазиимпульса электрона $p$ при различных значениях амплитуды напряженности электрического поля волны: 1 – ${{E}_{0}} = 0;$ 2 – ${{E}_{0}} = 0.6 \cdot {{10}^{6}}$; 3 – ${{E}_{0}} = 1.2 \cdot {{10}^{6}}$; 4 – ${{E}_{0}} = 1.8 \cdot {{10}^{6}}$ В ∙ см–1.
Представление функции распределения в форме (18) позволяет в явном виде найти ${{f}_{1}}.$ Перейдем в систему координат, в которой векторы напряженности постоянного и высокочастотного электрических полей ${{\vec {E}}_{1}}$ и ${{\vec {E}}_{0}}$ направлены вдоль оси Z. Из (6), (19) получаем:
Вычислим плотность тока вдоль оси Z:
(24)
$\begin{gathered} {{j}_{z}} = {{E}_{1}} \cdot \frac{{2n{{{\left( {kT} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\varepsilon _{{st}}^{2}}}{{\sqrt {2\pi m} {{n}_{{ci}}} \cdot {{{\left( {Ze} \right)}}^{2}}}}\int\limits_0^{\pi } {d\alpha \sin \alpha {{{\cos }}^{2}}\alpha } \times \\ \times \,\,\int\limits_0^\infty {dp\frac{{\exp \left( { - {{p}^{2}}} \right){{p}^{3}}}}{{J\left( {p,\alpha } \right)}}} = \sigma {{E}_{1}}. \\ \end{gathered} $Удельная проводимость, вычисленная согласно (24), равна $\sigma = 13.5$ (Ом ∙ м)–1, что при концентрации носителей заряда $n\sim {{10}^{{16}}}$ см–3 соответствует подвижности $\mu = 85$ см2 ∙ (В ∙ с)–1. При расчетах полагали ${{E}_{0}}\sim 0.6 \cdot {{10}^{6}}$ В ∙ см–1.
Таким образом, на основе анализа квантового кинетического уравнения, учитывающего рассеяние электронов на заряженных примесях, исследовано влияние сильной электромагнитной волны, вектор напряженности которой ${{\vec {E}}_{0}}$ коллинеарен с вектором напряженности постоянного электрического поля ${{\vec {E}}_{1}},$ на проводимость оксида галлия. Показано, что вплоть до значений ${{E}_{0}}\sim {{10}^{5}}$ В ∙ см–1 основную роль играют упругие процессы, поэтому можно непосредственно ввести время релаксации. Вычисленные значения подвижности по порядку величины совпадают с наблюдаемыми в эксперименте.
Работа выполнена при финансовой поддержке Минобрнауки России на выполнение государственных работ в сфере научной деятельности в рамках проектной части государственного задания, код проекта 3.2797.2017/4.6, и при финансовой поддержке РФФИ и Администрации Волгоградской области в рамках научного проекта 18-42-340006 р_а.
Список литературы
Кукушкин С.А., Николаев В.И., Осипов А.В. и др. // ФТТ. 2016. Т. 58. № 9. С. 1812; Kukushkin S.A., Nikolaev V.I., Osipov A.V. et al. // Phys. Sol. St. 2016. V. 58. № 9. P. 1876.
Stepanov S.I., Nikolaev V.I., Bougrov V.E. et al. // Rev. Adv. Mater. Sci. 2016. V. 44. P. 63.
Konishi K., Goto K., Murakami H. et al. // Appl. Phys. Lett. 2017. V. 110. Art. № 103506.
Irmscher K., Galazka Z., Pietsch M. et al. // J. Appl. Phys. 2011. V. 110. Art. № 063720.
Peelaers H., Van de Walle Ch.G. // Appl. Phys. Lett. 2017. V. 111. Art. № 182104.
Parisini A., Fornari R. // Semicond. Sci. Technol. 2016. V. 31. Art. № 035023.
Ma N., Tanen N., Verma A. et al. // Appl. Phys. Lett. 2016. V. 109. Art. № 212101.
Ghosh K., Singisetti U. // Appl. Phys. Lett. 2016. V. 109. Art. № 072102.
Ghosh K., Singisetti U. // J. Mater. Res. 2017. V. 32. Art. № 4142.
Ghosh K., Singisetti U. // J. Appl. Phys. 2017. V. 122. Art. № 035702.
Parisini A., Ghosh K., Singisetti U. et al. // Semicond. Sci. Technol. 2018. V. 33. Art. № 105008.
Kang Y., Krishnaswamy K., Peelaers H. et al. // J. Phys. Cond. Matt. 2017. V. 29. Art. № 234001.
Эпштейн Э.М. // ФТТ. 1969. Т. 11. № 10. С. 2732.
Поляновский В.М. // ЖЭТФ. 1980. Т. 79. № 6(12). С. 2189.
Zhang Zi-Ch., Wu Ye, Lu Ch., Ahmed Sh. // Appl. Phys. A. 2018. V. 124. P. 637.
Бонч-Бруевич В.Л., Калашников С.Г. Физика полупроводников. М.: Наука, 1977. 672 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая
Пн.-пт.: 10.00-19.00