1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 1, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 1, стр. 38-42

Высшие гармоники плотности тока в двумерной сверхрешетке на основе графена в условиях воздействия внешних электрических полей с учетом ионизации примеси

П. В. Бадикова 1, С. Ю. Глазов 1,  2, *, Г. А. Сыродоев 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Волгоградский государственный социально-педагогический университет”
Волгоград, Россия

2 Федеральное государственное бюджетное образовательное учреждение высшего образования “Волгоградский государственный медицинский университет”
Волгоград, Россия

* E-mail: ser-glazov@yandex.ru

Поступила в редакцию 29.07.2019
После доработки 30.08.2019
Принята к публикации 27.09.2019

Полный текст (PDF)

Аннотация

Исследована зависимость амплитуд высших гармоник плотности тока в двумерной сверхрешетке на основе графена от характеристик приложенных к системе постоянного и переменного электрических полей c учетом ионизации примесных центров. При определенных соотношениях параметров примесей и приложенных полей выявлено значительное преобладание одних гармоник над другими.

ВВЕДЕНИЕ

Внимание к нелинейным электромагнитным процессам вызвано возможностью их использования как при исследовании физических свойств наноструктур, так и для управления характеристиками электромагнитного излучения, что находит свое применение в оптике и наноэлектронике. Интерес к проблеме генерации высших гармоник обусловлен перспективой создания источников когерентного излучения терагерцового диапазона. Экспериментальному исследованию возможностей генерации таких гармоник квантовыми полупроводниковыми сверхрешетками (СР) посвящены работы [1, 2]. В последнее время внимание исследователей сосредоточено на изучении структур на основе графена. Генерация второй гармоники в графене исследована экспериментально [3, 4] и теоретически [5]. Совместное влияние постоянного и переменного электрических полей на высшие гармоники тока изучено для углеродных нанотрубок [6], щелевого графена [7], одномерных графеновых СР (ГСР) [8, 9]. Представляет интерес изучение свойств двумерных (2D) ГСР. В [10] сообщается о новом подходе к изготовлению 2D ГСР, в котором сверхрешеточный потенциал модулируется подложкой с периодическими наноотверстиями. В работе [11] исследована уникальная 2D СР, полученная в результате осаждения графена на подложку из металлических наношаров. Обобщение идеи получения одномерной ГСР на двумерный случай выполнено в работах [12, 13], в которых исследуется влияние внешних электрических полей на транспортные свойства 2D ГСР.

Случайные дефекты, редкие примеси могут приводить к появлению в запрещенной зоне ГСР примесных уровней, с которых электроны имеют возможность перейти в зону проводимости за счет теплового движения или под воздействием внешних электрических полей. В [14] проведен учет ионизации примесных центров в квазиклассически сильных электрических полях методом мнимого времени, который приводит к росту амплитуды гармоники за счет увеличения концентрации носителей заряда в минизоне проводимости.

В силу вышеизложенного, актуальным представляется исследование возможности генерации высших гармоник в 2D ГСР при совместном влиянии постоянного и переменного электрических полей c учетом ионизации примесных центров.

ОСНОВНЫЕ УРАВНЕНИЯ

Энергетический спектр носителей заряда в 2D ГСР в приближении сильной связи выбран в виде [12]

(1)
$\varepsilon (\vec {p}) = \pm \Delta \sqrt {f_{1}^{2} + f_{2}^{2}\left( {1 - \cos ({{{{p}_{x}}{{d}_{1}}} \mathord{\left/ {\vphantom {{{{p}_{x}}{{d}_{1}}} \hbar }} \right. \kern-0em} \hbar })} \right) + f_{3}^{2}\left( {1 - \cos ({{{{p}_{у}}{{d}_{2}}} \mathord{\left/ {\vphantom {{{{p}_{у}}{{d}_{2}}} \hbar }} \right. \kern-0em} \hbar })} \right)} ,$
где Δ − полуширина запрещённой зоны щелевой модификации графена, коэффициенты fi подбираются численно на основе непосредственного решения дисперсионного соотношения из [15], $\vec {p} = ({{p}_{x}},{{p}_{y}})$ – вектор квазиимпульса электрона, di = dI + dII − период СР (i = 1, 2), dI и dII − ширина полосок бесщелевого и щелевого графена. Разные знаки относятся к минизоне проводимости и валентной минизоне.

Для расчета рассмотрим случай симметричной 2D ГСР с d1= d2= d = 2 ∙ 10–6 см. Численный расчет дает коэффициенты аппроксимации f1 = 0.4217, f2 = f3 = 0.3318, ширину запрещенной зоны между валентной минизоной и минизоной проводимости εg = 0.8573Δ; ширину запрещенной зоны между первой и второй минизонами проводимости εg12= 0.6270Δ; ширину первой минизоны проводимости εe = 0.2111Δ.

Использовался квазиклассический подход, при котором закон дисперсии носителей заряда определялся аппроксимацией квантово-механического расчета [14], а вычисление электрического тока производилось с помощью классического кинетического уравнения Больцмана с модельным интегралом столкновений Батнагара–Гросса–Крука. Для нахождения гармоник тока использовалось разложение в ряд Фурье

(2)
$\begin{gathered} j\left( t \right) = {{a}_{0}} + \sum\limits_{l = 1}^\infty {\left( {{{a}_{l}}\cos l\omega t + {{b}_{l}}\sin l\omega t} \right)} , \\ {{a}_{l}} = {{j}_{0}}{{B}_{{ion}}}\sum\limits_{k,m = - \infty }^\infty {\sum\limits_{n = 1}^\infty {{{A}_{{nm}}}{{C}_{{nm}}}{{J}_{k}}({{D}_{{nm}}})} } {{J}_{{k + l}}}({{D}_{{nm}}})\,\left[ {\sin {{\varphi }_{{(k + l)nm}}}\cos {{\varphi }_{{(k + l)nm}}} + } \right. \\ \left. { + \,\,{{{( - 1)}}^{l}}\sin {{\varphi }_{{ - (k + l)nm}}}\cos {{\varphi }_{{(k + l)nm}}}} \right], \\ {{b}_{l}} = - {{j}_{0}}{{B}_{{ion}}}\sum\limits_{k,m = - \infty }^\infty {\sum\limits_{n = 1}^\infty {{{A}_{{nm}}}{{C}_{{nm}}}{{J}_{k}}({{D}_{{nm}}})} } {{J}_{{k + l}}}({{D}_{{nm}}})\,\left[ {\sin \varphi _{{_{{(k + l)nm}}}}^{2} - {{{( - 1)}}^{l}}\sin \varphi _{{_{{ - (k + l)nm}}}}^{2}} \right], \\ \end{gathered} $
где ${{j}_{0}} = {{ - ed{{n}_{0}}\Delta } \mathord{\left/ {\vphantom {{ - ed{{n}_{0}}\Delta } {2\hbar }}} \right. \kern-0em} {2\hbar }},$ n0 – концентрация электронов в зоне проводимости, Bion = 1 + + $\frac{N}{{{{n}_{0}}}}\frac{{\exp ( - 2\sigma \operatorname{Im} S)}}{{{{\tau }_{0}}{{\nu }_{r}} + \exp ( - 2\sigma \operatorname{Im} S)}},$ N – концентрация примесей в графене, $\sigma = {\Delta \mathord{\left/ {\vphantom {\Delta {\nu \hbar }}} \right. \kern-0em} {\nu \hbar }},$ $\gamma = {\nu \mathord{\left/ {\vphantom {\nu {{{\nu }_{r}}}}} \right. \kern-0em} {{{\nu }_{r}}}},$ τ0 – время туннелирования, νr – частота рекомбинации, ν – частота столкновений, Jn(x) – функция Бесселя 1-го рода n-го порядка, $\xi (x,y)$ = $\sqrt {f_{1}^{2} + f_{2}^{2}(2 - \cos x - \cos y)} ,$ ${{C}_{{nm}}}$ = $\int_{ - {\pi }}^{\pi } {\int_{ - {\pi }}^{\pi } {\cos (nx)\cos (my)\exp \left( { - \delta \xi (x,y)} \right)} } dxdy,$ $D{}_{{nm}}$ = ${{n{{F}_{{0x}}}} \mathord{\left/ {\vphantom {{n{{F}_{{0x}}}} w}} \right. \kern-0em} w} + {{m{{F}_{{0y}}}} \mathord{\left/ {\vphantom {{m{{F}_{{0y}}}} w}} \right. \kern-0em} w},$ $w = {\omega /\nu },$ $\sin {{\varphi }_{{knm}}}$ = = ${{(1 + {{(n{{F}_{{1x}}} + m{{F}_{{1y}}} + kw)}^{2}})}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$ $\delta = {\Delta \mathord{\left/ {\vphantom {\Delta {{{k}_{{\text{Б}}}}T}}} \right. \kern-0em} {{{k}_{{\text{Б}}}}T}},$ ${{A}_{{nm}}}$ = = $\frac{1}{{{{C}_{{00}}}}}\frac{{f_{2}^{2}}}{{2{{\pi }^{2}}}}\int_{ - {\pi }}^{\pi } {\int_{ - {\pi }}^{\pi } {\sin \left( x \right)\sin (nx)\cos (my)\xi {{{(x,y)}}^{{ - 1}}}dxdy} } ,$ ${{\vec {F}}_{1}}$ = $\left\{ {{{de{{E}_{{1x}}}} \mathord{\left/ {\vphantom {{de{{E}_{{1x}}}} {\hbar \nu }}} \right. \kern-0em} {\hbar \nu }},{{de{{E}_{{1y}}}} \mathord{\left/ {\vphantom {{de{{E}_{{1y}}}} {\hbar \nu }}} \right. \kern-0em} {\hbar \nu }}} \right\},$ ${{\vec {F}}_{0}}$ = $\{ {{de{{E}_{{0x}}}} \mathord{\left/ {\vphantom {{de{{E}_{{0x}}}} {\hbar \nu }}} \right. \kern-0em} {\hbar \nu }},$ ${{de{{E}_{{0y}}}} \mathord{\left/ {\vphantom {{de{{E}_{{0y}}}} {\hbar \nu }}} \right. \kern-0em} {\hbar \nu }}\} .$ Амплитуда l-ой гармоники плотности тока определяется выражением ${{j}_{l}} = \sqrt {а_{l}^{2} + b_{l}^{2}} .$

Время туннелирования τ0 определяется из решения трансцендентного уравнения

(3)
$ch[x({{\tilde {\tau }}_{0}})] + ch[y({{\tilde {\tau }}_{0}})] = \frac{{2f_{2}^{2} + f_{1}^{2} - {{{({{f}_{1}} - \tilde {\upsilon })}}^{2}}}}{{f_{2}^{2}}},$
где ${{\tilde {\tau }}_{0}} = {{\tau }_{0}}\nu ,$ $x({{\tilde {\tau }}_{0}})$ = ${{{{F}_{{1x}}}{{{\tilde {\tau }}}_{0}} + {{F}_{{0x}}}sh(w{{{\tilde {\tau }}}_{0}})} \mathord{\left/ {\vphantom {{{{F}_{{1x}}}{{{\tilde {\tau }}}_{0}} + {{F}_{{0x}}}sh(w{{{\tilde {\tau }}}_{0}})} w}} \right. \kern-0em} w},$ $y({{\tilde {\tau }}_{0}})$ = = ${{{{F}_{{1y}}}{{{\tilde {\tau }}}_{0}} + {{F}_{{0y}}}sh(w{{{\tilde {\tau }}}_{0}})} \mathord{\left/ {\vphantom {{{{F}_{{1y}}}{{{\tilde {\tau }}}_{0}} + {{F}_{{0y}}}sh(w{{{\tilde {\tau }}}_{0}})} w}} \right. \kern-0em} w},$ $\tilde {\upsilon } = {\upsilon \mathord{\left/ {\vphantom {\upsilon \Delta }} \right. \kern-0em} \Delta }.$

Учитывая, что выход частицы из-под барьера происходит при t = 0 [14], находим мнимую часть действия, входящего в вероятность ионизации примеси

(4)
$\operatorname{Im} S = \int\limits_0^{{{{{\tilde {\tau }}}}_{0}}} {\left\{ {\sqrt {f_{1}^{2} + f_{2}^{2}\left( {2 - ch\left[ {x(t)} \right] - ch\left[ {y(t)} \right]} \right)} + (\tilde {\upsilon } - {{f}_{1}})} \right\}} dt.$

ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Непосредственно из анализа формулы (2) следует, что амплитуды четных гармоник тока в случае отсутствия постоянного поля (Е1 = 0) равны нулю. При этом нечетные гармоники тока присутствуют. Аналогичный вывод о генерации нечетных гармоник в одномерных ГСР под воздействием переменного электрического поля приведен в работе [8].

Как видно из (2), вследствие неаддитивности энергетического спектра и учета столкновений, гармоники плотности тока, текущего вдоль исследуемого направления, зависят как от напряженности постоянного и амплитуды переменного электрических полей, поляризованных вдоль этого направления, так и от параметров полей, ориентированных перпендикулярно. Дальнейший анализ формулы (2) в силу ее сложности выполняли численно.

Зависимость амплитуд гармоник плотности тока от характеристик, приложенных к системе полей имеет немонотонный осциллирующий характер. Это дает возможность в широком интервале значений управлять амплитудой гармоник, усиливая одни и подавляя другие.

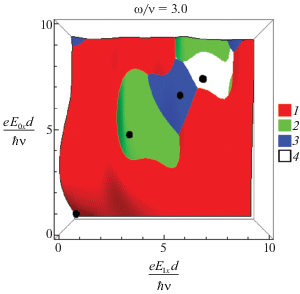
Рассмотрим случай, когда электрические поля поляризованы вдоль оси х. На рис. 1 показаны области значений полей для первых четырех гармоник, амплитуда каждой из которых превосходит три остальные для фиксированной частоты переменного электрического поля. Особенно перспективным в плане практического приложения представляется начальная область полей, поскольку именно здесь амплитуда осцилляций максимальна.

Рис. 1.

Карта максимумов первых четырех гармоник: F0y = F1y = 0, w = 3.0.

Для оценки эффективности генерации гармоник введен коэффициент

(5)
${{К}_{{\text{Э}}}} = {{({{j}_{i}} - {{j}_{k}})} \mathord{\left/ {\vphantom {{({{j}_{i}} - {{j}_{k}})} {{{j}_{i}}}}} \right. \kern-0em} {{{j}_{i}}}},$
где i – номер преобладающей гармоники из рассматриваемых четырех, k – номер гармоники, следующей по амплитуде. Жирными точками на рис. 1 отмечены положения максимумов этих коэффициентов. При увеличении частоты переменного поля происходит сдвиг максимумов амплитуд гармоник в сторону более сильных полей.

В табл. 1 приведены эффективные значения гармоник плотности тока, в безразмерных единицах. Для первой гармоники подобное значение всегда находится в начальной области полей вне зависимости от частоты. При увеличении частоты сдвиг максимумов для остальных трех гармоник происходит в область более сильных полей. При определенных соотношениях параметров можно добиться ситуации, когда первую гармонику превосходят остальные.

Таблица 1.  

Эффективные значения гармоник плотности тока

w 2 гармоника 3 гармоника 4 гармоника
F1x F0x j2/j0 F1x F0x j3/j0 F1x F0x j4/j0
0.2 1.2063 0.8625 0.011060 4.0750 4.2750 0.020973 9.9375 10.2875 0.015265
0.5 1.4500 1.3813 0.022077 4.1125 4.2625 0.018742 8.7500 9.1500 0.015789
1.0 1.7188 1.8250 0.028894 5.4375 5.9063 0.020480 9.2688 9.8063 0.015371
1.5 1.9563 2.4000 0.038897 6.4813 7.1625 0.020667 3.1375 10.2188 0.029918
2.0 2.3063 3.1250 0.044812 8.5063 9.8625 0.021354 2.1125 10.3875 0.030272
2.5 2.7188 3.9188 0.048452 0.0000 9.7938 0.049748 6.0625 6.3875 0.019990
3.0 3.1625 4.7188 0.050569 5.8625 6.8313 0.032695 7.1875 7.8000 0.020321
3.5 3.6438 5.4813 0.051320 6.8625 7.9563 0.033088 8.2313 9.31875 0.020831
4.0 4.1313 6.2500 0.051839 7.8813 9.0688 0.033273 9.8250 10.3875 0.017105

Исследована зависимость коэффициента нелинейных искажений (коэффициент гармоник) от параметров приложенных полей. Расчет коэффициента выполнен по следующей формуле [17]

(6)
${{К}_{{\text{Г}}}}(\omega ) = \frac{{\sqrt {j_{2}^{2} + j_{3}^{2} + ... + j_{n}^{2}} }}{{{{j}_{1}}}}.$

На рис. 2 представлена зависимость коэффициента гармоник от частоты, для полей, соответствующих максимумам второй (а) и третьей (б) гармоники при частоте w = 2.0 и второй (в) и третьей (г) гармоники при w = 4.0 (см. табл. 1).

Рис. 2.

Зависимость коэффициента гармоник от частоты, F0y = F1y = 0: w = 2.0: (a) F1x = 2.30625, F0x = = 3.125, (б) F1x = 8.50625, F0x = 9.8625; w = 4.0: (в) F1x = = 4.13125, F0x = 6.25, (г) F1x = 7.88125, F0x = 9.06875.

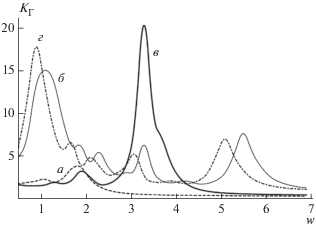
Коэффициент нелинейных искажений в начальной области частот может принимать значения больше единицы и имеет немонотонный осциллирующий характер. Начиная с некоторой характерной частоты, определяемой величиной электрических полей, первая гармоника преобладает над остальными, коэффициент KГ (ω) убывает, становясь меньше единицы. По графику KГ (ω) можно определить частоту, при которой наблюдается наибольшее преобладание высших гармоник над первой. При увеличении напряженности постоянного и амплитуды переменного электрических полей увеличивается область частот, в которых существенны нелинейные искажения.

Рассмотрим случай произвольной поляризации электрических полей. Вследствие неаддитивности энергетического спектра ГСР появляется возможность управления амплитудами гармоник поперечными электрическими полями. На рис. 3 приведена зависимость амплитуды первой гармоники от амплитуды переменного электрического поля при фиксированных значениях напряженности постоянного поля приложенного вдоль оси y, частоты и параметров полей поляризованных вдоль оси х. В отсутствии примесей (а) эффективность воздействия поперечных электрических полей на амплитуды гармоник в ГСР меньше по сравнению с щелевым графеном [16], из-за отличия их энергетических спектров (наличия произведения косинусов от разных компонент квазиимпульса в спектре щелевого графена). Резкое возрастание амплитуды гармоники (б, в) определяется ионизацией примеси, причем для более глубоких примесей (в) начало роста сдвигается в сторону более сильных полей.

Рис. 3.

Зависимость амплитуды первой гармоники от амплитуды переменного электрического поля приложенного вдоль оси y, при фиксированных знамениях F0x = F1x = 2.7, F1y = 0, w = 3.0: (a) без учета ионизации примеси, (б) с учетом ионизации примеси $\tilde {\upsilon } = 0.1{{f}_{1}},$ (в) с учетом ионизации примеси $\tilde {\upsilon } = 0.14{{f}_{1}}.$

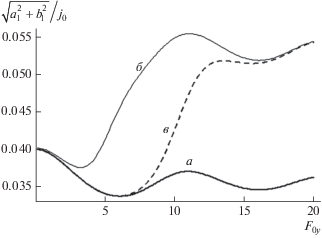
Удобно для аналитических расчетов использовать разложение (1) в двойной ряд Фурье. В работе [14] показано, что с увеличением периода ГСР уменьшается влияние неаддитивности энергетического спектра и при d > 5 ∙ 10–6 см, можно с хорошей степенью точности аппроксимировать “истинный” спектр структуры аддитивной зависимостью энергии от квазиимпульса. В рассматриваемом в работе частном случае (d = 2 ∙ 10–6 см) энергетический спектр обладает слабой неаддитивностью, что и проявляется в слабой зависимости амплитуд гармоник от поперечного электрического поля. При уменьшении периода ГСР возможность управления амплитудами гармоник поперечными электрическими полями увеличивается.

Зависимость амплитуд гармоник плотности тока от угла φ между вектором поляризации переменного электрического поля и осью х, при фиксированных значениях параметров внешних электрических полей показана на рис. 4. Угол α задает поворот вектора напряженности постоянного электрического поля по отношению к оси х. Параметры полей выбраны в области эффективного значения третьей гармоники. На рис. 4 наблюдается асимметрия jl(φ), связанная с анизотропией, наведенной постоянным электрическим полем, и самого спектра ГСР. Поворотом вектора поляризации переменного электрического поля можно добиться преобладания одной гармоники над другими. Подбор примеси заданной глубины и учет их ионизации приводит к возможности существенного управления амплитудой гармоники.

Рис. 4.

Зависимость амплитуд гармоник плотности тока от угла поворота вектора поляризации переменного электрического поля, при α = π/6, F0 = 7.0, F1 = = 6.0, w = 3.0: (a) первая гармоника, (б) вторая гармоника, (в) третья гармоника.

Сделаем численные оценки: значения безразмерных напряженностей F0, 1 = 1 соответствуют E0, 1 ≈ 30 В ∙ см–1, а безразмерной частоте w = 1 соответствует ω = 1011 Гц, N = 5 ∙ 1010 см–2, n0= 1011 см–2, νr = 107 Гц, T ≈ 70 К.

ЗАКЛЮЧЕНИЕ

Получено и численно проанализировано выражение для амплитуд высших гармоник плотности тока в 2D ГСР под воздействием постоянного и переменного электрических полей. Выявлена возможность управления амплитудами гармоник поперечными электрическими полями. По сравнению с щелевым графеном, эффективность воздействия поперечных электрических полей на амплитуды гармоник в 2D ГСР меньше из-за существенного отличия их энергетических спектров. Зависимость амплитуд гармоник плотности тока от характеристик приложенных к системе полей имеет немонотонный осциллирующий характер. Это дает возможность в широком интервале значений управлять амплитудой гармоник. В результате комплексного анализа выявлены области параметров рассматриваемой системы для первых четырех гармоник, амплитуды каждой из которых превосходят три остальные.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-42-340005 и Минобрнауки России на выполнение государственных работ в сфере научной деятельности в рамках проектной части государственного задания, код проекта: 3.2797.2017/4.6.

Список литературы

  1. Вакс В.Л., Панин А.Н., Басов С.А. и др. // Изв. вузов. Радиофиз. 2009. Т. 52. № 7. С. 569; Vaks V.L., Panin A.N., Basov S.A. et al. // Radiophys. Quant. Electron. 2009. V. 52. № 7. P. 511.

  2. Павельев Д.Г., Кошуринов Ю.И., Иванов А.С. и др. // ФТП. 2012. Т. 46. № 1. С. 125; Paveliev D.G., Koshurinov Y.I., Ivanov A.S. et al. // Semiconductors. 2012. V. 46. № 1. P. 121.

  3. Dean J.J., Driel H.M. // Appl. Phys. Lett. 2009. V. 95. Art. № 261910.

  4. Dean J.J., Driel H.M. // Phys. Rev. B. 2010. V. 82. Art. № 125411.

  5. Глазов М.М. // Письма в ЖЭТФ. 2011. Т. 93. № 7. С. 408; Glazov M.M. // JETP Lett. 2011. V. 93. № 7. P. 366.

  6. Белоненко М.Б., Глазов С.Ю., Мещерякова Н.Е. // Опт. и спектрос. 2010. Т. 108. № 5. С. 818; Belonenko M.B., Glazov S.Yu., Meshcheryakova N.E. // Opt. Spectrosс. 2010. V. 108. № 5. P. 774.

  7. Бадикова П.В., Глазов С.Ю. // Изв. РАН. Сер. физ. 2015. Т. 79. № 12. С. 1650; Badicova P.V., Glazov S.Yu. // Bull. Russ. Acad. Sci. Phys. 2015. V. 79. № 12. P. 1443.

  8. Глазов С.Ю., Мещерякова Н.Е. // Наносистемы: физ., хим., матем. 2012. Т. 3. № 1. С. 64.

  9. Глазов С.Ю., Мещерякова Н.Е., Мартынов Д.В. // Изв. РАН. Сер. физ. 2012. Т. 76. № 12. С. 1475; Glazov S.Yu., Mescheryakova N.E., Martynov D.V. // Bull. Russ. Acad. Sci. Phys. 2012. V. 76. № 12. P. 1319.

  10. Forsythe C., Zhou X., Watanabe K. et al. // Nat. Nanotechn. 2018. V. 13. P. 566.

  11. Zhang Y., Kim Y., Gilbert M.J. et al. // arXiv: 1703.05689 [cond-mat.mes-hall]. 2018.

  12. Kryuchkov S.V., Popov C.A. // J. Nano. Electron. Phys. 2017. V. 9. № 2. P. 02013.

  13. Kryuchkov S.V., Popov C.A. // Proc. 2017 IEEE 7th Int. Conf. Nanomat. Appl. Prop. (Odessa, 2017). P. 03CBN09.

  14. Бадикова П.В., Глазов С.Ю., Сыродоев Г.А. // ФТП. 2019. Т. 53. № 7. С. 927; Badikova P.V., Glazov S.Yu., Syrodoev G.A. // Semiconductors. 2019. V. 53. № 7. P. 911.

  15. Ратников П. В. // Письма в ЖЭТФ. 2009. Т. 90. № 6. С. 515; Ratnikov P.V. // JETP Lett. 2009. V. 90. № 6. P. 469.

  16. Глазов С.Ю. // Изв. РАН. Сер. физ. 2019. Т. 83. № 1. С. 19; Glazov S.Yu. // Bull. Russ. Acad. Sci. Phys. 2019. V. 83. № 1. P. 12.

  17. Афонский А.А., Дьяконов В.П. Электронные измерения в нанотехнологиях и микроэлектронике. Москва: ДМК Пресс, 2011. 688 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал