Известия РАН. Серия физическая, 2020, T. 84, № 1, стр. 43-47
О плазменных волнах в 2D-кристаллах с учетом расщепления Рашбы
Е. И. Кухарь 1, 2, *, С. В. Крючков 1, 2, В. И. Конченков 2
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Волгоградский государственный социально-педагогический университет”,
Лаборатория физики низкоразмерных систем
Волгоград, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Волгоградский государственный технический университет”
Волгоград, Россия
* E-mail: eikuhar@yandex.ru
Поступила в редакцию 29.07.2019
После доработки 30.08.2019
Принята к публикации 27.09.2019
Аннотация
Исследовано дисперсионное соотношение для плазменных волн в двумерных структурах с расщеплением Рашбы. Изучено влияние высокочастотного электромагнитного излучения на энергию плазмонов. Показана возможность появления точек излома в функциональной зависимости кривизны дисперсионной линии от энергии Ферми и от интенсивности высокочастотного излучения.
ВВЕДЕНИЕ
Спиновое расщепление электронных состояний в 2D-материалах приводит к формированию в их зонной структуре так называемых дираковких (конических) точек, характерных для двумерных (2D) дираковских (графеноподобных) кристаллов [1–3]. Спиновые состояния электронов в полупроводниковых структурах и проблемы спиновой динамики являются объектами повышенного внимания исследователей в связи с интенсивным развитием спинтроники и технологии гетероструктур [4–6]. Одной из основных задач этих областей является создание электронных устройств с перестраиваемыми характеристиками [7–10]. Современные достижения как в области физики твердого тела, так и в области наноэлектроники, дают возможность управления электронными свойствами дираковских 2D-структур и топологических изоляторов за счет изменения внешних электромагнитных (ЭМ) полей [10–18].
Изучение спин-зависимых явлений в низкоразмерных системах играет важную роль в разработке устройств хранения и обработки информации [19]. Преимуществом низкоразмерных систем является зависимость интенсивности спин-орбитального взаимодействия от параметров структуры [4, 20, 21] (геометрические размеры, интенсивность удержания, эффективная масса и т.д.). Например, в [22] предложено использование циркулярно поляризованного оптического излучения для управления спинами электронов в квантовых точках.
Исследования плазменных волн и коллективных возбуждений, называемых плазмонами, в дираковских 2D-кристаллах и топологических изоляторах актуальны как с фундаментальной [23], так и с практической точек зрения [20]. Фундаментальный интерес объясняется тем фактом, что такие квантовомеханические объекты как плазмоны не имеют аналогов в классической теории. Более того, учет взаимодействия носителей заряда в дираковских 2D-кристаллах с плазмонами в ряде ситуаций является определяющим для объяснения особенностей формирования электрон-плазмонных [24, 25] и магнитоплазмонных [26] комплексов. Практический интерес к таким объектам связан с возможностью увеличения быстродействия электронных устройств, использующих в своей работе плазмонную динамику [27, 28]. Последнее объясняется тем фактом, что групповая скорость плазмонов превышает дрейфовую скорость электронов на несколько порядков.
ЭНЕРГИЯ ПЛАЗМОНОВ В 2D-КРИСТАЛЛАХ С РАСЩЕПЛЕНИЕМ РАШБЫ
Считаем, что 2D-структура лежит в плоскости $xy$. Учет спин-орбитального взаимодействия и размерное квантование вдоль оси $Oz$ приводят к появлению линейных по квазиимпульсу $\vec {p}$ слагаемых в спектре носителей заряда, которые имеют вид [4, 23] (модель Рашбы):
(1)
$\hat {H} = \frac{{\hat {p}_{x}^{2} + \hat {p}_{y}^{2}}}{{2m}} + {{v}_{{{\text{SO}}}}}\left( {{{{\hat {p}}}_{y}}{{{\hat {\sigma }}}_{x}} - {{{\hat {p}}}_{x}}{{{\hat {\sigma }}}_{y}}} \right),$(2)
${{\varepsilon }_{n}}\left( {\vec {p}} \right) = \frac{{{{p}^{2}}}}{{2m}} + {{\left( { - 1} \right)}^{n}}{{{v}}_{{{\text{SO}}}}}p,\,\,\,\,n = 1,2.$Согласно (2) состояние с $p = 0$ $\left( {\varepsilon = 0} \right)$ оказывается вырожденным по спину и соответствует пересечению двух дисперсионных ветвей ($n$ = 1, 2). Плазмонные возбуждения в 2D-структурах с расщеплением Рашбы исследовались в приближении случайных фаз (ПСФ) в работе [23] для случая высоких концентраций электронов, когда уровень Ферми превышал энергию, отвечающую $p = 0$ $\left( {{{\varepsilon }_{{\text{F}}}} > 0} \right).$ Ниже исследуется зависимость энергии плазмонов от положения уровня Ферми в том случае, когда последний оказывается ниже значения $\varepsilon = 0.$ Кроме того, изучается влияние ВЧ ЭМ-излучения на энергию плазмонов в 2D-кристалле с расщеплением Рашбы. Температуры электронного газа предполагаются предельно низкими.
В рамках ПСФ закон дисперсии для плазмонов находится из уравнения
где $V\left( {\vec {k}} \right) = {{2\pi {{e}^{2}}} \mathord{\left/ {\vphantom {{2\pi {{e}^{2}}} k}} \right. \kern-0em} k}$ – потенциал неэкранированного взаимодействия электронов, которое предполагается кулоновским [24, 28], $\Pi \left( {\omega ,\vec {k}} \right)$ – поляризационный оператор, вычисляемый по формуле(4)
$\Pi \left( {\omega ,\vec {k}} \right) = i\int {{{G}_{0}}\left( {{{\varepsilon }_{ + }},{{{\vec {p}}}_{ + }}} \right){{G}_{0}}\left( {{{\varepsilon }_{ - }},{{{\vec {p}}}_{ - }}} \right)\frac{{{\text{d}}\varepsilon {{{\text{d}}}^{2}}\vec {p}}}{{{{{\left( {2\pi \hbar } \right)}}^{3}}}}} ,$${{G}_{0}}\left( {\varepsilon ,\vec {p}} \right)$ – причинная функция Грина для электрона, ${{\vec {p}}_{ \pm }} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {p} \pm {{\hbar \vec {k}} \mathord{\left/ {\vphantom {{\hbar \vec {k}} 2}} \right. \kern-0em} 2},$ ${{\varepsilon }_{ \pm }} = \varepsilon \pm {{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } 2}} \right. \kern-0em} 2}.$ В случае предельно низких температур существование плазмонов возможно, если выполняется условие ${{\varepsilon }_{{\text{F}}}} > - {{\Delta }_{{{\text{SO}}}}},$ где ${{\Delta }_{{{\text{SO}}}}} = {{m{v}_{{{\text{SO}}}}^{{\text{2}}}} \mathord{\left/ {\vphantom {{m{v}_{{{\text{SO}}}}^{{\text{2}}}} 2}} \right. \kern-0em} 2}.$ В противном случае уровень Ферми оказывается внутри запрещенной зоны. После некоторых преобразований имеем следующее выражение:
(5)
$\begin{gathered} \Pi \left( {\omega ,\vec {k}} \right) = \frac{1}{{2\pi {{\hbar }^{2}}}}\left[ {\frac{{{{p}_{2}}}}{{\left| {{{v}_{{1,2}}}} \right|}}\left( {\frac{\omega }{{\sqrt {{{\omega }^{2}} - v_{{1,2}}^{2}{{k}^{2}}} }} - 1} \right)} \right. + \\ + \,\,\frac{{{{p}_{1}}}}{{\left| {{{v}_{{1,1}}}} \right|}}\left( {\frac{\omega }{{\sqrt {{{\omega }^{2}} - v_{{1,1}}^{2}{{k}^{2}}} }} - 1} \right)\theta \left( { - {{\varepsilon }_{{\text{F}}}}} \right) + \\ + \,\,J\left. {\frac{{{{p}_{1}}}}{{\left| {{{v}_{{2,1}}}} \right|}}\left( {\frac{\omega }{{\sqrt {{{\omega }^{2}} - v_{{2,1}}^{2}{{k}^{2}}} }} - 1} \right)\theta \left( {{{\varepsilon }_{{\text{F}}}}} \right)} \right] \\ \end{gathered} $.Здесь $\theta \left( x \right)$ – ступенчатая функция, ${{v}_{{n,i}}} = {{v}_{n}}\left( {{{p}_{i}}} \right),$ ${{v}_{n}} = {{\partial }_{p}}{{\varepsilon }_{n}},$ ${{\varepsilon }_{n}}\left( p \right)$ – электронный спектр (2), ${{p}_{i}}$ – корни уравнения $\varepsilon \left( p \right) = {{\varepsilon }_{{\text{F}}}},$ равные
(6)
${{p}_{i}} = m{{v}_{{{\text{SO}}}}}\left| {1 + {{{\left( { - 1} \right)}}^{i}}\sqrt {1 + \frac{{{{\varepsilon }_{{\text{F}}}}}}{{{{\Delta }_{{{\text{SO}}}}}}}} } \right|,\,\,\,\,i = 1,2.$Известно, что в длинноволновом приближении закон дисперсии плазмонов в 2D-структурах имеет вид $\omega \propto \sqrt k ,$ где $\vec {k}$ – волновой вектор плазмона. Коэффициент пропорциональности определяет групповую скорость плазменных волн и зависит от электронных свойств материала. Данный коэффициент пропорционален кривизне дисперсионной линии для плазмонов в точке $k = 0.$
В длинноволновом приближении ($\hbar k \ll m{{{v}}_{{{\text{SO}}}}}$) вместо (5) приходим к следующему выражению
(7)
$\begin{gathered} \Pi \left( {\omega ,\vec {k}} \right) = \frac{{{{k}^{2}}}}{{4\pi {{\hbar }^{2}}{{\omega }^{2}}}} \times \\ \times \,\,\left[ {{{p}_{1}}\left( {\left| {{{v}_{{1,1}}}} \right|\theta \left( { - {{\varepsilon }_{{\text{F}}}}} \right) + {{v}_{{2,1}}}\theta \left( {{{\varepsilon }_{{\text{F}}}}} \right)} \right) + {{p}_{2}}{{v}_{{1,2}}}} \right]. \\ \end{gathered} $С помощью соотношения (3) находим энергию плазмона:
(8)
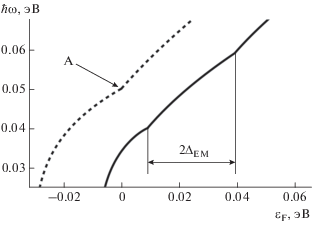
$\hbar \omega = e\sqrt {2{{\Delta }_{{{\text{SO}}}}}k} \times \left\{ \begin{gathered} {{\left( {1 + \frac{{{{\varepsilon }_{{\text{F}}}}}}{{{{\Delta }_{{{\text{SO}}}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},\,\,\,\, - {{\Delta }_{{{\text{SO}}}}} < {{\varepsilon }_{{\text{F}}}} < 0, \hfill \\ {{\left( {1 + \frac{{{{\varepsilon }_{{\text{F}}}}}}{{{{\Delta }_{{{\text{SO}}}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{\varepsilon }_{{\text{F}}}} > 0. \hfill \\ \end{gathered} \right.$Зависимость энергии плазмона от энергии Ферми показана на рис. 2 (пунктирная линия, $\hbar k = 0.1m{{v}_{{{\text{SO}}}}}$). На графике видна точка излома A, которая, согласно (8), достигается, когда уровень Ферми пересекает значение $\varepsilon = 0.$
ВЛИЯНИЕ ВЫСОКОЧАСТОТНОГО ИЗЛУЧЕНИЯ НА ДИСПЕРСИОННУЮ ЛИНИЮ ПЛАЗМОНОВ
Известно, что внешние возмущения могут приводить к снятию вырождения. Здесь в качестве внешнего воздействия на 2D-материал рассматривается высокочастотное (ВЧ) ЭМ-излучение, которое приводит к расщеплению состояний с квазиимпульсом $p = 0,$ отвечающим пересечению ветвей закона дисперсии (1). Предполагается, что ЭМ-излучение с частотой $\Omega $ и с амплитудой напряженности электрического поля ${{E}_{0}}$ распространяется вдоль оси $Oz$ так, что в плоскости $xy$ векторный потенциал этого поля имеет вид:
(9)
$\vec {A}\left( t \right) = - \frac{{c{{E}_{0}}}}{\Omega }\left\{ {\sin \Omega t,\,\,\,\,\sin \left( {\Omega t + \varphi } \right)} \right\}.$Спинор $\psi ,$ описывающий движение 2D-электрона в поле ЭМ-волны удовлетворяет следующему уравнению:
(10)
$i\hbar \frac{{\partial \psi }}{{\partial t}} = \frac{{{{{\hat {\vec {\pi }}}}^{2}}\psi }}{{2m}} + {{v}_{{{\text{so}}}}}\left( {{{{\hat {\pi }}}_{y}}{{{\hat {\sigma }}}_{x}} - {{{\hat {\pi }}}_{x}}{{{\hat {\sigma }}}_{y}}} \right)\psi .$Здесь $\hat {\vec {\pi }} = \hat {\vec {p}} + {{e\vec {A}} \mathord{\left/ {\vphantom {{e\vec {A}} c}} \right. \kern-0em} c}.$ Решение уравнения (10) подчиняется теореме Флоке:
(11)
$\psi \left( t \right) = u\left( t \right){{e}^{{ - \;\frac{{i\tilde {\varepsilon }t}}{\hbar }}}},$(12)
${{\hat {H}}_{{eff}}} = \frac{{\hat {p}_{x}^{2} + \hat {p}_{y}^{2}}}{{2m}} + {{v}_{{{\text{SO}}}}}\left( {{{{\hat {p}}}_{y}}{{{\hat {\sigma }}}_{x}} - {{{\hat {p}}}_{x}}{{{\hat {\sigma }}}_{y}}} \right) + {{\Delta }_{{{\text{EM}}}}}{{\hat {\sigma }}_{z}} + {{\Delta }_{0}},$${{\Delta }_{0}} = {{p_{{{\text{EM}}}}^{2}} \mathord{\left/ {\vphantom {{p_{{{\text{EM}}}}^{2}} {2m}}} \right. \kern-0em} {2m}},$ ${{p}_{{{\text{EM}}}}} = {{e{{E}_{0}}} \mathord{\left/ {\vphantom {{e{{E}_{0}}} \Omega }} \right. \kern-0em} \Omega },$ ΔEM = ${{p_{{{\text{EM}}}}^{2}v_{{{\text{SO}}}}^{{\text{2}}}\sin \varphi } \mathord{\left/ {\vphantom {{p_{{{\text{EM}}}}^{2}v_{{{\text{SO}}}}^{{\text{2}}}\sin \varphi } {\hbar \Omega }}} \right. \kern-0em} {\hbar \Omega }}.$ Собственные значения (12) имеют вид:
(13)
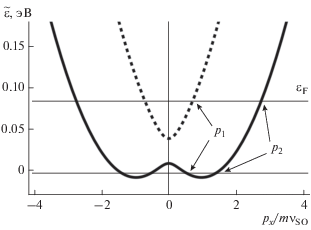
${{\tilde {\varepsilon }}_{n}}\left( p \right) = \frac{{{{p}^{2}}}}{{2m}} + {{\left( { - 1} \right)}^{n}}\sqrt {\Delta _{{{\text{EM}}}}^{2} + v_{{{\text{SO}}}}^{{\text{2}}}{{p}^{2}}} + {{\Delta }_{0}},\,\,\,\,n = 1,2.$В отсутствие ВЧ-поля $\left( {{{E}_{0}} = 0} \right)$ формула (13) дает закон дисперсии (2), состоящий из двух ветвей, пересекающихся в точке $\vec {p} = 0$ [4, 23], что соответствует вырождению состояния по спину. В присутствии ВЧ-поля $\left( {{{E}_{0}} \ne 0} \right)$ происходит разделение этих ветвей в указанной точке, что связано со снятием вырождения (рис. 1), а также смещение спектра вверх по энергии на величину ${{\Delta }_{0}}.$ Величина расщепления в окрестности точки $\vec {p} = 0$ равна $2{{\Delta }_{{{\text{EM}}}}}.$ При фиксированной интенсивности волны максимальное расщепление возникает в случае круговой поляризации $\left( {\varphi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right).$ Для линейно поляризованной волны $\left( {\varphi = 0} \right)$ ${{\Delta }_{{{\text{EM}}}}} = 0.$
Поляризационный оператор с учетом (13) равен
(14)
$\begin{gathered} \Pi \left( {\omega ,\vec {k}} \right) = \frac{{{{k}^{2}}}}{{4\pi {{\hbar }^{2}}{{\omega }^{2}}}} \times \\ \times \,\,\left[ {{{p}_{1}}\left( {\left| {{{v}_{{1,1}}}} \right|\theta \left( { - {{{\tilde {\varepsilon }}}_{{\text{F}}}} - {{\Delta }_{{{\text{EM}}}}}} \right) + {{v}_{{2,1}}}\theta \left( {{{{\tilde {\varepsilon }}}_{{\text{F}}}} - {{\Delta }_{{{\text{EM}}}}}} \right)} \right) + {{p}_{2}}{{{\tilde {v}}}_{{1,2}}}} \right], \\ \end{gathered} $(15)
$\begin{gathered} {{p}_{i}} = \sqrt 2 m{{v}_{{{\text{SO}}}}} \times \\ \times \,\,\sqrt {1 + \frac{{{{{\tilde {\varepsilon }}}_{{\text{F}}}}}}{{2{{\Delta }_{{{\text{SO}}}}}}} + {{{\left( { - 1} \right)}}^{i}}\sqrt {{{{\left( {1 + \frac{{{{{\tilde {\varepsilon }}}_{{\text{F}}}}}}{{2{{\Delta }_{{{\text{SO}}}}}}}} \right)}}^{2}} - \frac{{\tilde {\varepsilon }_{{\text{F}}}^{2} - \Delta _{{{\text{EM}}}}^{2}}}{{4\Delta _{{{\text{SO}}}}^{2}}}} } , \\ i = 1,2. \\ \end{gathered} $С помощью соотношения (3) находим энергию плазмона:
(16)
$\hbar \omega = e\sqrt {\frac{k}{2}\left[ {{{p}_{1}}\left( {\left| {{{{\tilde {v}}}_{{1,1}}}} \right|\theta \left( { - {{{\tilde {\varepsilon }}}_{{\text{F}}}} - {{\Delta }_{{{\text{EM}}}}}} \right) + {{{\tilde {v}}}_{{2,1}}}\theta \left( {{{{\tilde {\varepsilon }}}_{{\text{F}}}} - {{\Delta }_{{{\text{EM}}}}}} \right)} \right) + {{p}_{2}}{{{\tilde {v}}}_{{1,2}}}} \right]} .$Зависимость энергии плазмона от энергии Ферми, построенная по формуле (16), показана на рис. 2 (сплошная линия, $\hbar k = 0.1m{{v}_{{{\text{SO}}}}}$). На графике видно, что действие ВЧ-поля приводит к возникновению двух точек излома вместо одной, как это было в отсутствие излучения. Разница энергий, отвечающих этим точкам, равна $2{{\Delta }_{{{\text{EM}}}}}.$ Причиной этого эффекта является, во-первых, снятие вырождения по спину в точке $p = 0$ и, во-вторых, образование в окрестности этой точки области с отрицательными эффективными массами. Действительно, если ${{\varepsilon }_{{\text{F}}}} < {{\Delta }_{0}} - {{\Delta }_{{{\text{EM}}}}},$ уровень Ферми пересекает нижнюю дисперсионную ветвь (сплошная линия на рис. 3) в двух точках ${{p}_{1}}$ и ${{p}_{2}}$, одна из которых $\left( {{{p}_{1}}} \right)$ приходится на область отрицательных эффективных масс. По мере увеличения энергии Ферми точка пересечения, отвечающая квазиимпульсу ${{p}_{1}},$ смещается вверх, пока не наступит условие ${{\varepsilon }_{{\text{F}}}} = {{\Delta }_{0}} - {{\Delta }_{{{\text{EM}}}}}.$ В этом случае вклад электронов из области отрицательных эффективных масс прекратится. Последнее равенство, таким образом, определяет первую точку излома в функциональной зависимости энергии плазмона от энергии Ферми. В ситуации, когда уровень Ферми оказывается внутри области расщепления между верхней и нижней дисперсионными линиями $\left( {{{\Delta }_{0}} - {{\Delta }_{{{\text{EM}}}}} < {{\varepsilon }_{{\text{F}}}} < {{\Delta }_{0}} + {{\Delta }_{{{\text{EM}}}}}} \right),$ вклад в плазменные колебания вносят только электроны с импульсом ${{p}_{2}}.$ Равенство ${{\varepsilon }_{{\text{F}}}} = {{\Delta }_{0}} + {{\Delta }_{{{\text{EM}}}}}$ определяет вторую точку излома. Начиная с момента, когда уровень Ферми становится по энергии выше значения ${{\Delta }_{0}} + {{\Delta }_{{{\text{EM}}}}},$ вклад в плазменные колебания начинают давать электроны, дисперсия которых определяется верхней дисперсионной линией (пунктирная линия на рис. 1).
Рис. 3.
Зависимость энергии плазмона от параметра ${{\Delta }_{{{\text{EM}}}}}$ при $\hbar k = 0.1m{{v}_{{{\text{SO}}}}}.$ Сплошная линия – $\hbar \Omega $ = = $15{{\Delta }_{{{\text{SO}}}}},$ пунктирная линия – $\hbar \Omega $ = $20{{\Delta }_{{{\text{SO}}}}},$ штрихпунктирная линия – $\hbar \Omega $ = $30{{\Delta }_{{{\text{SO}}}}}.$
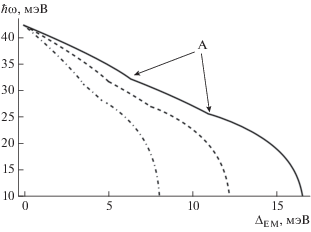
Отметим, что, согласно (16), кривизной дисперсионной линии плазмонов, а также их групповой скоростью можно управлять, меняя интенсивность ВЧ-излучения. Последнее может представлять интерес для приложений, использующих устройства с перестраиваемыми характеристиками, работу которых определяет динамика плазмонов. Графики зависимости энергии плазмона от интенсивности ВЧ-излучения, построенные для различных значений частоты $\Omega $, показаны на рис. 3, где также видны точки излома, обозначенные буквой A. В частности, если амплитуда ВЧ-излучения удовлетворяет неравенству $p_{{{\text{EM}}}}^{2} > 2m\left( {{{\Delta }_{{{\text{SO}}}}} + {{\varepsilon }_{{\text{F}}}}} \right),$ то плазменные колебания подавляются (здесь предполагается, что $\hbar \Omega \gg {{\Delta }_{{{\text{SO}}}}}$).
ЗАКЛЮЧЕНИЕ
Нами было исследовано влияние спин-орбитального взаимодействия и ВЧ-излучения на дисперсионную линию для плазмонов в 2D-кристаллах с расщеплением Рашбы. Показана возможность изменения характера зависимости от энергии Ферми энергии плазмонов в том случае, когда уровень Ферми проходит через состояние, вырожденное по спину. Кроме того, продемонстрировано изменение энергии плазмонов с фиксированным значением волнового числа путем изменения интенсивности ВЧ-излучения, которому подвергается образец. Для этой функциональной зависимости характерно наличие двух точек излома (рис. 3). Наличие ЭМ-излучения приводит к расщеплению по энергии двух дисперсионных ветвей, отвечающих различным проекциям спина в точке $p = 0.$ Величина расщепления равна $2{{\Delta }_{{{\text{EM}}}}}$ (рис. 1). Если интенсивность ВЧ-поля и концентрация носителей заряда таковы, что выполняется неравенство ${{\varepsilon }_{{\text{F}}}} > {{\Delta }_{0}} + {{\Delta }_{{{\text{EM}}}}},$ то уровень Ферми пересекает обе дисперсионные ветви, описываемые формулой (13). На рис. 1 точкам пересечения соответствуют состояния с квазиимпульсами ${{p}_{1}}$ и ${{p}_{2}}.$ По мере увеличения интенсивности волны дисперсионные ветви смещаются вверх по энергии, а величина расщепления ${{\Delta }_{{{\text{EM}}}}}$ растет так, что импульс ${{p}_{1}}$ стремится к нулю, и при ${{p}_{1}} = 0$ (${{\varepsilon }_{{\text{F}}}} = {{\Delta }_{0}} + {{\Delta }_{{{\text{EM}}}}}$) вклад электронов, состояния которых отвечают верхней дисперсионной ветви (пунктирная линия на рис. 1), прекращается. Этот факт определяет первую точку излома в функциональной зависимости энергии плазмона от интенсивности волны. В ситуации, когда уровень Ферми лежит между верхней и нижней дисперсионными линиями $\left( {{{\Delta }_{0}} - {{\Delta }_{{{\text{EM}}}}} < {{\varepsilon }_{{\text{F}}}} < {{\Delta }_{0}} + {{\Delta }_{{{\text{EM}}}}}} \right),$ вклад в плазменные колебания вносят только электроны с импульсом ${{p}_{2}}.$ Условие, при котором уровень Ферми начинает пересекать нижнюю дисперсионную линию (сплошная линия на рис. 1) в двух точках, одна из которых приходится на область отрицательных эффективных масс, определяет вторую точку излома $\left( {{{\varepsilon }_{{\text{F}}}} = {{\Delta }_{0}} - {{\Delta }_{{{\text{EM}}}}}} \right).$
Описанная выше зависимость энергии плазмонов от интенсивности падающего излучения дает возможность для управления кривизной дисперсионной линии плазмонов, а также их групповой скоростью путем изменения амплитуды ВЧ-поля. Последнее может представлять интерес для приложений, использующих устройства с перестраиваемыми характеристиками, работу которых определяет динамика плазмонов.
Работа выполнена при финансовой поддержке Минобрнауки России на выполнение государственных работ в сфере научной деятельности в рамках проектной части государственного задания, код проекта: 3.2797.2017/4.6.
Список литературы
Hirahara T., Miyamoto K., Matsuda I. et al. // Phys. Rev. B. 2007. V. 76. Art. № 153305.
Shikin A.M., Varykhalov A., Prudnikova G.V. et al. // Phys. Rev. Lett. 2008. V. 100. Art. № 057601.
Miyamoto K., Kimura A., Kuroda K. et al. // Phys. Rev. Lett. 2012. V. 108. Art. № 066808.
Tang C.S., Mal’shukov A.G., Chao K.A. // Phys. Rev. B. 2005. V. 71. Art. № 195314.
Appelbaum I., Huang B., Monsma D.J. // Nature. 2007. V. 447. P. 295.
Joshi V.K. // Eng. Sci. Technol. 2016. V. 19. P. 1503.
Mohammadpour H. // J. Magn. Magn. Mater. 2015. V. 385. P. 129.
Hofmann M., Chiang W.-Y., Nguyen T.D. et al. // Nano-technology. 2015. V. 26. Art. № 335607.
Guo X., Wang W., Nan H. et al. // Optica. 2016. V. 3. P. 1066.
Sheremet A.S., Kibis O.V., Kavokin A.V. et al. // Phys. Rev. B. 2016. V. 93. Art. № 165307.
Iurov A., Gumbs G., Roslyak O. et al. // J. Phys. Cond. Matt. 2013. V. 25. Art. № 135502.
Rodriguez-Lopez P., Betouras J.J., Savel’ev S.E. // Phys. Rev. B. 2014. V. 89. Art. № 155132.
Usaj G., Perez-Piskunow P.M., Foa Torres L.E.F. et al. // Phys. Rev. B. 2014. V. 90. Art. № 115423.
Kryuchkov S.V., Kukhar E.I., Konchenkov V.I. // Adv. Stud. Theor. Phys. 2014. V. 8. P. 731.
Cea P. // Eur. Phys. J. B. 2016. V. 89. Art. № 104.
Yuan X.-X., He L., Wang S.-T. et al. // Chin. Phys. Lett. 2017. V. 34. Art. № 060302.
Wu L., Patankar S., Morimoto T. et al. // Nat. Phys. 2017. V. 13. P. 350.
Champo A.E., Naumis G.G. // Phys. Rev. B. 2019. V. 99. Art. № 035415.
Datta S., Das B. // Appl. Phys. Lett. 1990. V. 56. P. 665.
Tavares M.R.S. // Sol. State Commun. 2009. V. 149. P. 923.
O’Connor D., Ginzburg P., Rodríguez-Fortuño F.J. et al. // Nat. Commun. 2014. V. 5. P. 5327.
Berezovsky J., Mikkelsen M.H., Stoltz N.G. et al. // Science. 2008. V. 320. P. 349.
Wang X.F. // Phys. Rev. B. 2005. V. 72. Art. № 085317.
Scholz A., Stauber T., Schliemann J. // Phys. Rev. B. 2012. V. 86. Art. № 195424.
Pyatkovskiy P.K., Chakraborty T. // Phys. Rev. B. 2016. V. 93. Art. № 085145.
Lozovik Y.E., Sokolik A.A. // Nanoscale Res. Lett. 2012. V. 7. P. 134.
Grigorenko A.N., Polini M., Novoselov K.S. // Nat. Photon. 2012. V. 6. P. 749.
Peragut F., Cerutti L., Baranov A. et al. // Optica. 2017. V. 4. P. 1409.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая