Известия РАН. Серия физическая, 2020, T. 84, № 11, стр. 1553-1559

ВВЕДЕНИЕ

Спектроскопия ядерного магнитного резонанса (ЯМР) основана на реакции атомных ядер на внешние магнитные поля: частоты отклика ядер зависят от их окружения, поэтому ЯМР дает информацию о молекулярной структуре образца, а также о происходящих в нем химических и физических процессах. ЯМР-спектроскопия – один из наиболее широко используемых в органической химии инструментов для идентификации неизвестных соединений. Она используется в биохимии для идентификации белков и других сложных молекул и выявления их структуры в пространстве, а также как инструмент для мониторинга химических реакций.

Особенно информативны многомерные ЯМР-эксперименты, поскольку они выявляют корреляции между несколькими атомами. Однако они занимают много времени, особенно если необходимо получить спектры с высоким отношением “сигнал/шум”. На сегодняшний день широко распространена практика использования неоднородной выборки сигнала: некоторые точки измерения в высших измерениях пропускаются для сокращения времени эксперимента [1]. В дальнейшем применяется реконструкция, основанная на некоторых предполагаемых свойствах спектров. Существует несколько подходов к реконструкции. Одним из них является семейство алгоритмов реконструкции сжатых измерений (СИ). Реконструкция СИ основана на свойстве спектральной разреженности: из всех возможных спектров, которые соответствовали бы неполным измерениям, она выбирает самый разреженный [2–4]. Спектральная разреженность здесь означает, что ЯМР-спектр в основном “пустой”, с небольшим диапазоном частот, покрытых пиками. Это предположение верно во многих практических случаях [5].

Поиск ортогонального соответствия (ПОС) [6] является одним из алгоритмов СИ, используемых для реконструкции разреженного вектора $x \in {{C}^{n}}$ на основе небольшого числа измерений. ПОС и родственные алгоритмы (например, сжатое соответствии выборки [7] и кусочно-ортогональный поиск соответствия [8]), в отличие от минимизаторов l_p-нормы (например, итеративный мягкий порог [9], итеративный метод наименьших квадратов с меняющимися весам [10]), принадлежат к группе жадных алгоритмов, то есть таких, которые выбирают локально оптимальное решение в каждой итерации.

Математически СИ формулируется с помощью матрицы измерения $A \in {{M}_{{m \times n}}}\left( C \right),$ которая при применении к разреженным векторам $x \in {{C}^{n}}$ дает вектор измерения $y = Ax \in {{C}^{m}}.$ Эрмитово сопряжение матрицы измерения обозначим A*. Разреженность х определяется кардинальным числом носителя его функции: ${\text{supp}}~x = {\text{\{ }}i:{{x}_{i}} \ne 0{\text{\} ,}}$ ${\text{\# supp\;}}x \ll n.$ Доказано, что при определенных условиях для матрицы измерений А результат ПОС согласуется с вектором х. Эти условия – когерентности и ограниченной изометрии – описаны в [6] и [11] соответственно. Обозначим столбцы А через ${{a}_{i}} \in {{C}^{m}}.$ Когерентность μ матрицы А определяется как $\mu = \mathop {{\text{max}}}\limits_{i \ne j} \left| {{{a}_{i}}*{{a}_{j}}} \right|,$ где $i,j \in {\text{\{ }}1,2, \ldots ,n{\text{\} }}{\text{.}}$ Cвойство s-ограниченной изометрии с константой изометрии $0 < {{\delta }_{s}} < 1,$ в свою очередь, удовлетворяется, если для каждого вектора, такого, что #supp x ≤ s, выполняется условие

Идею алгоритма ПОС можно схематически описать при помощи следующих основных блоков:

Вход: матрица измерения $A \in {{M}_{{m \times n}}}\left( C \right);$ вектор измерения $y \in {{C}^{m}};$ параметр точности ε > 0.

Индексы ненулевых координат ПОС хранятся во множестве $I \subset {\text{\{ }}1,2, \ldots ,n{\text{\} }}{\text{.}}$ За одну итерацию множество I увеличивается на один индекс $I \mapsto I \cup {\text{\{ }}\iota {\text{\} ,}}$ где

и ι не может быть впоследствии удалено из I.

Стандартным критерием остановки для ПОС является точность ε. Математические аспекты этого критерия остановки были исследованы в работе [12], где ПОС рассматривался в контексте строго разреженного вектора х, при измерениях дающего величину $y = Ax + \varepsilon {\kern 1pt} '.$ Основной результат [12] гласит, что если ненулевые компоненты х достаточно велики, а когерентность А достаточно мала, то при пороге точности $\varepsilon = {{\left\| {{{\varepsilon }^{'}}} \right\|}^{2}}$ результат ПОС не допускает ненулевой компоненты вне supp x, т.е I ⊂ suppx. Несомненно, это результат большой теоретической и практической значимости. Однако его применение требует хорошей оценки уровня шума. Его подробное описание будет приведено в следующем разделе, где мы также сравниваем его с модификацией ПОС, основанной на концепции перекрестной валидации (ПВ): ПОС-ПВ (см. [13]). В дальнейшем ПОС по типу “складного ножа” (СН), рассматриваемый в данной работе, будет обозначаться как ПОС-СН. Приведем краткое описание ПОС-СН, позволяющее нам связать его с идеей СН, которая используется в статистике [14].

Метод СН – это инструмент, используемый для оценки некоторой стохастической величины θ. Пусть у нас есть N наблюдений. Опуская одно из них, получаем соответствующую оценку ${{\theta }_{i}},$ где $i \in {\text{\{ }}1,2, \ldots ,N{\text{\} }}$ соответствует индексу пропущенного измерения. Оценкой СН для величины θ по определению является среднее значение ${{\theta }_{{{\text{CH}}}}} = \frac{1}{N}\sum\nolimits_{i = 1}^N {{{\theta }_{i}}} .$

В ПОС-СН мы можем разделить вектор измерения y на определенное число (например, 4) подмножеств с приблизительно равными кардинальными числами. Опустив одну группу измерений, мы получим четыре оценки: ${{x}^{1}},{{x}^{2}},{{x}^{3}},{{x}^{4}}$ для x, каждая из которых основана на приблизительно 75% имеющихся измерений. Сравнивая четыре результата ПОС, можно отметить сильную нестабильность положения ложных компонент и найти положения ненулевых компонент, которые входят в ${{x}^{i}}$ для каждого i. На последнем этапе мы не следуем непосредственно методу СН. Вместо вычисления средней величины ${{x}^{i}},$ мы выполняем алгоритм ПОС на основе всех измерений, и в качестве дополнительного ограничения для ПОС используем ранее полученные позиции стабильных пиков.

Многие сигналы имеют спектры, которые состоят из относительно небольшого числа хорошо определенных, хотя и не разреженных пиков. Например, спектр, полученный в ЯМР-эксперименте, обычно состоит из нескольких лоренцовых пиков, и они не являются строго разреженными. Модификация ПОС, учитывающая эту особенность, была введена в [15]. Вместо того, чтобы добавлять одну ненулевую компоненту, модифицированный алгоритм за одну итерацию добавляет к спектру целый лоренцовый пик. Такой алгоритм получил название поиска соответствия лоренцовых пиков (ПСЛП). Тесты алгоритма [15] показывают, что при правильно подобранном критерии остановки ПСЛП превосходит другие алгоритмы СН для ЯМР-спектров. Однако подобно ПОС, ПСЛП может пропускать определенные пики или помещать в спектр ложные пики, если не подобрать критерий остановки правильно. Схема алгоритма ПСЛП представлена ниже, где мы также формулируем и тестируем версию ПСЛП-СН, отмечая ее преимущества перед ПСЛП-СИ.

ПОС ПО ТИПУ “СКЛАДНОЙ НОЖ”: ПОС-СН

Рассмотрим вектор ${v} \in {{C}^{n}},$ носитель функции которого supp v имеет кардинальное число k $ \ll $ n. Пусть $\lambda \in {{R}_{ + }}$ – абсолютное значение наименьшей ненулевой координаты v

Подчеркнем, что подход к шуму отличается от используемого в [12], т.е. мы используем вектор шума $\varepsilon \in {{C}^{n}},$ который приводит к искажениям вида x = v + ε. Для численных тестов ПОС-СН предположим, что ${{\left\| \varepsilon \right\|}_{\infty }} < \frac{1}{5}\lambda ,$ что обосновано практическими рекомендациями по анализу ЯМР-спектров: пики, не превышающие по размеру шум в 5 раз, рассматриваются как артефакты.

Пусть $F \in {{M}_{{m \times n}}}\left( C \right)$ будет n-мерной матрицей преобразования Фурье. В эксперименте с ЯМР-спектрами с пропущенными измерениями схема выборки вводится путем задания случайных подмножеств $T \subset {\text{\{ }}1,2, \ldots ,n{\text{\} }}$ с кардинальным числом m < n. Таким образом, матрица измерения $A \in {{M}_{{m \times n}}}\left( C \right)~$ состоит из строк F с элементами T в качестве индексов. Поскольку вектор измерения y можно записать в виде $y = A{v} + \varepsilon {\kern 1pt} ',$ где $\varepsilon {\kern 1pt} '$ = Aε, наш подход можно соотнести с тем, который принят в [12]. Мы будем говорить, что вектор ε определяет шум.

Применяя алгоритм ПОС для восстановления v, мы заметили, что:

– если допускается большее количество итераций ПОС, чем количество ненулевых компонент в векторе v, то результат ПОС содержит ненулевые координаты, которые находятся за пределами supp v;

– абсолютные значения компонент вне supp v в этом случае больше, чем уровень шума ε;

– позиции таких компонент сильно неустойчивы по отношению к изменению схемы выборки T.

Основываясь на этих наблюдениях, мы вводим версию ПОС по принципу “складного ножа”. Идея “складного ножа” объяснена в [14], а примеры ее применения в ЯМР-контексте есть в [16]. В нашем случае метод реализуется следующим образом:

(1) зафиксировать схему выборки Т и разбить ее на четыре случайно выбранных, разобщенных подмножества примерно равного кардинального числа $T = {{T}_{1}} \cup {{T}_{2}} \cup {{T}_{3}} \cup {{T}_{4}};$

(2) применить ПОС четыре раза с использованием схем выборки;

(3) $T \setminus {{T}_{i}},i = 1,2,3,4;$

(4) определить положения ненулевых компонент, которые являются стабильными при изменении схемы выборки;

(5) выполнить ПОС по полной схеме выборки Т и остановить алгоритм, как только очередной индекс i ∈ I не будет признан стабильным на этапе (3) алгоритма.

Мы разбиваем выборку Т именно на четыре подмножества в связи со следующими двумя требованиями:

– схемы выборки $T \setminus {{T}_{i}}$ должны быть достаточно богаты для восстановления вектора v;

– различия между схемами выборки $T \setminus {{T}_{i}}$ должны быть достаточно большими, чтобы генерировать нестабильность позиций ложных ненулевых компонент.

ПОС-СН связан с другой модификацией ПОС, основанной на концепции перекрестной валидации в СИ, введенной в работе [17]. В контексте ПОС эта идея получила дальнейшее развитие в работе [13] и известна под названием ПОС-СИ. В ней вектор измерения y делится на две части: основную, ${{y}_{{{\text{ПОС}}}}} = {{A}_{{{\text{ПОС}}}}}{v} + \varepsilon _{{{\text{ПОС}}}}^{'},$ используемую для алгоритма ПОС, и вспомогательную, ${{y}_{{{\text{ПВ}}}}} = {{A}_{{{\text{ПВ}}}}}{v} + \varepsilon _{{{\text{ПВ}}}}^{'},$ используемую для перекрестной валидации (ПВ). Число d итераций ПОС-СИ является частью входных параметров алгоритма, и критерий остановки ε не используется. Результат итерации под номером p ПОС на основе y_ПОС обозначается v ^p. Имея остаток $\varepsilon _{{{\text{ПВ}}}}^{p} = \left\| {{{y}_{{{\text{ПВ}}}}} - {{A}_{{{\text{ПВ}}}}}{{{v}}^{p}}} \right\|,$ вычисляем $o = \mathop {\arg {\text{min}}}\limits_{p \leqslant d} ~\varepsilon _{{{\text{ПВ}}}}^{p},$ и результатом всей процедуры ПОС-СИ является v ^o.

ПОС-СН отличается от ПОС-СИ следующим образом:

– ПОС-СН менее произволен при делении данных на измерительный вектор y_ПОС и вектор перекрестной валидации y_ПВ. ПОС-СИ использует только одну подгруппу данных для перекрестной валидации (например, y_ПВ = y₁), в то время как ПОС-СН повторяет процедуру с различными вариантами y_i, i =1, 2, 3, 4;

– ПОС-СН использует все данные измерений y для конечного восстановления x, в то время как в ПОС-СИ используется только y_ПОС.

Мы протестировали алгоритм, используя вектор $x \in {{C}^{{512}}},$ представленный на рис. 1а, который содержит 6 больших пиков и шум. Зафиксировав случайным образом схему выборки T ⊂ {1, 2, …, 512}, длиной в 80 элементов, мы получили вектор измерения $y \in {{C}^{{80}}}.$ Чтобы показать, как ПОС ведет себя с обычным критерием остановки, на рис. 1б мы представляем результат 15 итераций ПОС. Отметим появление 6 доминирующих компонент и еще 9 ложных ненулевых компонент, которые находятся далеко за пределами уровня шума.

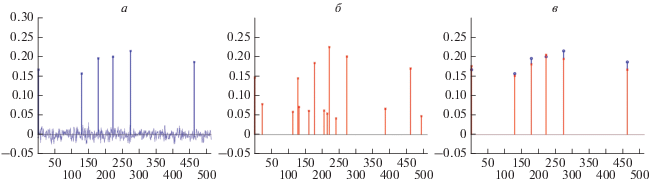
Выполняя ПОС-СН, мы применяем ПОС четыре раза на основе 60 измерений, выбранных из 80 так, как это было описано в предыдущем разделе. Это позволяет нам установить стабильные позиции пиков и приводит к успешному восстановлению вектора v, как показано на рис. 1в. Отметим, что, хотя пики в восстановленном спектре имеют другую высоту, их количество и позиции совпадают с компонентами входного вектора v. Более того, различия между входом (синие компоненты) и выходом (красные компоненты) находятся в пределах допуска, задаваемого уровнем шума.

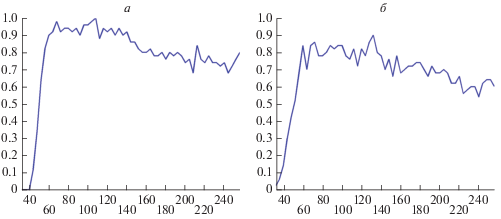
На рис. 2а представлены результаты систематического моделирования с длиной выборки, варьирующийся от 32 до 256 (горизонтальная ось). Для каждой длины мы генерируем 50 различных случайных схем выборки. На вертикальной оси показано относительное число успешных восстановлений спектра. Восстановление считается успешным, если оно содержит шесть ненулевых компонент, которые с точностью до уровня шума совпадают с ненулевыми компонентами v. Примечательно, что до определенной длины выборки (≈140) доля успешных восстанавливаний увеличивается с ростом длины. Выше этого числа она начинает несколько уменьшаться. Из анализа результатов ПОС-СН видно, что при достаточно большой выборке появляется одна искусственная ненулевая компонента. Алгоритм ПСЛП-СН, который будет рассмотрен в следующем разделе, не демонстрирует такого поведения.

Для сравнения ПОС-СН и ПОС-СН на рис. 2б показана статистика успешных восстановлений для ПОС-СИ. Видно, что ПОС-СН работает примерно на 10% лучше, чем ПОС-СИ. Примечательно, что преимущество метода СН перед СИ достигает порядка 25% для алгоритма ПСЛП, который обсуждается в следующем разделе.

ПСЛП ПО ТИПУ “СКЛАДНОЙ НОЖ”: ПСЛП-СН

ЯМР-спектр представляет собой комбинацию лоренцовых пиков

где $L_{l}^{j} \in {{C}^{n}}$ – нормализованный лоренцовый пик шириной j, с центром l, а $b_{{jl}}^{{}} \in C~~~$представляет интенсивность и фазу пика. При шуме $\varepsilon \in {{C}^{n}}$ получаем шумный спектр x = v + ε. При данной схеме измерения T ⊂ {1, 2, . . . . . , n}, #T = m вводим описанную ранее матрицу измерения $A \in {{M}_{{m \times n}}}\left( C \right),$ в результате чего получаем вектор измерения y = Ax. Псевдокод ПСЛП выглядит следующим образом:

Вход: матрица измерения $A \in {{M}_{{m \times n}}}\left( C \right);$ вектор измерения $y \in {{C}^{m}};$ параметр точности ε > 0; Лоренцовские пики $L_{l}^{j}$, j ∈ {0, 1, …, J}, l ∈ {1, 2, …, n}.

Более подробное описание ПСЛП приведено в [15].

Для выполнения ПСЛП-СН мы разделяем T на четыре случайно выбранных разобщенных подмножества примерно равного кардинального числа $T = {{T}_{1}} \cup {{T}_{2}} \cup {{T}_{3}} \cup {{T}_{4}}.$ Применяя ПСЛП четыре раза на основе схем выборки $T \setminus {{T}_{i}},i = 1,2,3,4,$ определяем позиции стабильных лоренцовых пиков. Позиция пиков стабильна, если с точностью до заданного допуска она возникает в каждом результате ПСЛП на основе $T \setminus {{T}_{i}}.$ Допуск оправдан особенностью ПСЛП, заключающейся в определении центров пиков с определенной точностью. В наших дальнейших симуляциях устанавливаем 2 спектральные точки в качестве такого допуска. После определения устойчивых позиций пиков выполняем ПСЛП по полной схеме выборки T.

Подчеркнем важное различие между конечными шагами ПСЛП-СН и ПОС-СН. ПОС-СН останавливает алгоритм, как только очередная координата не распознается как стабильная, в то время как в ПСЛП-СН появление пиков в нестабильной области становится маловероятным, при выполнении алгоритма фиксированное количество раз (в нашем случае 15). Как мы отметили при тестировании ПСЛП-СН, его остановка как в случае ПОС-СН работает неэффективно.

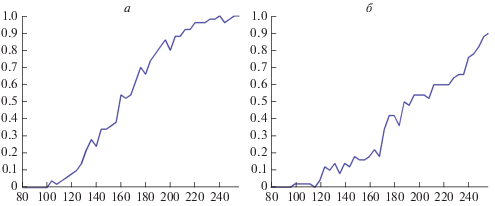
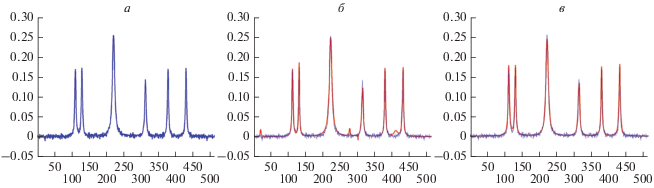
Мы протестировали алгоритм ПСЛП-СН на основе разреженного вектора $x \in {{C}^{{512}}},$ представленного на рис. 3а, содержащего 6 ненулевых пиков Лоренца и шум. Зафиксировав случайным образом схему выборки T ⊂ {1, 2, …, 512}, длиной в 180 элементов, получили вектор измерения $y \in {{C}^{{180}}}.$ На рис. 3б представлен результат 15 итераций ПСЛП. Запуск ПСЛП четыре раза, каждый раз на основе различных подвыборок из 135 измерений, позволил найти центры стабильных пиков и получить идеальное восстановление спектра, как показано на рис. 3в. В наших симуляциях допуск положения пика установлен на 2 спектральные точки. На рис. 4а представлены результаты систематического моделирования с длиной выборки, варьирующийся от 80 до 256 (горизонтальная ось). Для каждой длины генерируем 50 различных случайных схем выборки. На вертикальной оси отложено относительное число успешных восстановлений спектра. В контексте ПСЛП-СН мы даем другое определение идеального восстановления, которое оправдывается тенденцией ПСЛП помещать малые пики в окрестности больших пиков таким образом, чтобы это не влияло на форму восстановленного спектра. Если результат ПСЛП-СН состоит более чем из 6 пиков, но на самом деле видно только 6 из них, а остальные поглощаются доминирующими пиками, то мы говорим, что восстановление успешно. В ходе нашего исследования мы заметили, что этот случай соответствует тому, что остаток ПСЛП-СН менее чем в два раза превышает норму вектора шума ε. Мы приняли этот критерий в качестве определения успешного восстановления в ПСЛП-СН.

Примечательно, что преимущество подхода СН перед СИ, которое не было столь явным, когда мы сравнивали ПОС-СИ с ПОС-СН, теперь очевидно. Например, при выборке в 180 точек измерения количество успешных восстановлений для ПСЛП-СИ меньше 50%, в то время как алгоритм СН обеспечивает приблизительно 75%. Более того, как мы отметили в ходе наших тестов, ширина и высота пиков лучше согласуется с исходным спектром для ПСЛП-СН. Это можно объяснить тем, что, находя высоты и ширины пиков, ПСЛП-СН (в отличие от ПСЛП-СИ) использует все доступные измерения. Однако позиции пиков ограничены областью стабильных пиков, которая была установлена на предыдущем этапе на основе ограниченных данных. Статистика успешных восстановлений ПСЛП-СИ представлена на рис. 4б.

Данный подход может оказаться полезным и в других, отличных от ЯМР-спектроскопии, сферах, где применяются неполные измерения [18–20].

ЗАКЛЮЧЕНИЕ

Показано, что версия типа “складной нож” жадных алгоритмов сжатия измерений эффективно работает в контексте анализа данных ЯМР-экспериментов. В то время как для алгоритма поиска ортогонального соответствия наш метод лишь незначительно превосходит метод сжатия измерений, для поиска соответствия лоренцовых пиков он работает значительно более эффективно. Таким образом, можно заключить, что у алгоритма поиска соответствия лоренцовых пиков типа “складной нож” есть потенциал для применения в восстановлении экспериментальных неполных данных.

Работа выполнена при финансовой поддержке Фонда польской науки (проект First TEAM/2017-4/34).