1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 12, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 12, стр. 1739-1742

Влияние магнитного поля на эволюцию предельно коротких оптических импульсов в условиях нелинейного поглощения и накачки

М. Б. Белоненко 1, *, Н. Н. Конобеева 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Волгоградский государственный университет”
Волгоград, Россия

* E-mail: mbelonenko@yandex.ru

Поступила в редакцию 15.07.2020
После доработки 10.08.2020
Принята к публикации 26.08.2020

Полный текст (PDF)

Аннотация

Проанализировано влияние магнитного поля на распространение электромагнитных волн с учетом накачки и нелинейного поглощения, введенного феноменологически, в среде с зигзагообразными углеродными нанотрубками. Проанализирована зависимость формы импульса от величины магнитного поля и коэффициентов нелинейного поглощения.

ВВЕДЕНИЕ

Популярным направлением исследований в современной оптике является взаимодействие электромагнитного излучения с веществом в силу прикладного значения [1–3]. Важным моментом здесь являются возможности современных технологий в формировании мощного электромагнитного излучения с заданными характеристиками, в том числе предельно коротких лазерных импульсов [4], которые содержат только несколько колебаний электромагнитного поля. С другой стороны, немаловажным вопросом является выбор среды, в которой будут стабильно распространяться такие импульсы. Привлекательными с этой точки зрения являются углеродные наноструктуры, обладающие высоким потенциалом для применения в области разработки оптоэлектронных приборов, основанных на распространении нелинейных электромагнитных волн [5], в особенности углеродные нанотрубки (УНТ) [6]. Начиная с первой работы [7], были систематически изучены возможности распространения предельно коротких электромагнитных импульсов в массивах полупроводниковых углеродных нанотрубок с учетом влияния различных физических факторов [8–10]. Так в работе [11] исследовалось взаимодействие предельно короткого импульса со средой массива углеродных нанотрубок в условиях затухания, обусловленного пьезо-эффектом при колебаниях тяжелых ядер среды. В качестве способа компенсации диссипации и стабилизации импульса использовалось поле накачки. При этом важным вопросом остается изучение поведения импульса в среде под действием сильных внешних полей, в частности магнитного, чему и посвящена настоящая работа.

ОСНОВНЫЕ УРАВНЕНИЯ

Будем исследовать распространение двумерных предельно коротких оптических импульсов в массиве углеродных нанотрубок типа “зиг-заг”. Для определенности положим, что электромагнитный импульс распространяется перпендикулярно оси нанотрубок (ось 0y), а вектор его электрического поля коллинеарен оси 0z.

Векторный потенциал имеет вид: $\vec {A}$ = (0, 0, A(x, y)), плотность электрического тока $\vec {j} = \left( {0,0,j\left( {x,y} \right)} \right).$

Для компоненты электрического поля, направленной вдоль оси УНT (с учетом: $\vec {E} = - {{c}^{{ - 1}}}{{\partial{ \vec {A}}} \mathord{\left/ {\vphantom {{\partial{ \vec {A}}} {\partial t}}} \right. \kern-0em} {\partial t}},$ запишем двумерное волновое уравнение:

(1)
$\begin{gathered} \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{t}^{2}}}} - \Gamma \frac{{\partial{ \overrightarrow A} }}{{\partial t}} = \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{y}^{2}}}} + \frac{{4\pi }}{c}j\left( {\vec {A}} \right) - \\ - \,\,{{F}_{1}}{{\left( {\frac{{\partial{ \overrightarrow A} }}{{\partial t}}} \right)}^{3}} - \frac{{{{F}_{2}}\frac{{\partial{ \overrightarrow A} }}{{\partial t}}}}{{1 + \Delta {{{\left( {\frac{{\partial{ \overrightarrow A} }}{{\partial t}}} \right)}}^{2}}}} - \frac{{4\pi }}{c}\frac{{\partial{ \vec {P}}}}{{\partial t}}, \\ \end{gathered} $
где c – скорость света, параметр Γ описывает накачку электрического поля (за вычетом линейного поглощения) [12] и, соответственно, его усиление. Отметим, что накачка здесь введена феноменологически и, в общем случае, зависит только от пространственных координат, F1, F2 – коэффициенты нелинейного поглощения [13], вид и значение которых берутся из экспериментальных работ. Для учета свойств среды мы дополнили уравнение (1) слагаемым с поляризацией среды Р, направленной вдоль оси нанотрубок.

Запишем стандартное выражение для плотности тока [14]:

(2)
$j = 2e\sum\limits_{s = 1}^m {\int\limits_{ZB} {{{\upsilon }_{s}}\left( p \right)f\left( {p,s} \right)dp} } ,$
где e – заряд электрона, p – компонента квазиимпульса электрона проводимости вдоль оси нанотрубки, ${{\upsilon }_{s}}\left( p \right) = {{\partial {{\varepsilon }_{s}}\left( p \right)} \mathord{\left/ {\vphantom {{\partial {{\varepsilon }_{s}}\left( p \right)} {\partial p}}} \right. \kern-0em} {\partial p}}$ – скорость электронов, $f\left( {p,s} \right)$ – функция распределения Ферми, ${{\varepsilon }_{s}}\left( p \right)$ – закон дисперсии, который описывает свойства электронов УНТ и имеет вид [6, 15]:
(3)
${{\varepsilon }_{s}}\left( p \right) = {{\gamma }_{0}}\,\sqrt {1 + 4{\text{cos}}\left( {\frac{{3b}}{{2\hbar }}p} \right){\text{cos}}\left( {\frac{\pi }{m}\left( {s + \frac{\Phi }{{{{\Phi }_{0}}}}} \right)} \right) + 4{\text{co}}{{{\text{s}}}^{2}}\left( {\frac{\pi }{m}\left( {s + \frac{\Phi }{{{{\Phi }_{0}}}}} \right)} \right)} ,$
где s = 1, 2 …m, нанотрубка имеет тип (m, 0), γ0 ≈ ≈ 2.7 эВ, b = 0.142 нм – расстояние между соседними атомами углерода, Φ – магнитный поток через поперечное сечение УНТ, ${{\Phi }_{0}} = \frac{{\hbar с}}{e}$ – квант магнитного потока [16].

В итоге получаем эффективное уравнение на одну компоненту векторного потенциала:

(4)
$\begin{gathered} \frac{{{{\partial }^{2}}A}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}A}}{{\partial {{y}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}A}}{{\partial {{t}^{2}}}} + \\ + \,\,\sum\limits_{k = 1}^\infty {\frac{{4{{e}^{2}}{{n}_{0}}{{\gamma }_{0}}{{r}_{k}}}}{{{{c}^{2}}}}{\text{sin}}\left( {\frac{{3bke\left( {A + \eta } \right)}}{{2\hbar c}}} \right)} f\left( t \right) - {{F}_{1}}{{\left( {\frac{{\partial A}}{{\partial t}}} \right)}^{3}} - \\ - \,\,\frac{{{{F}_{2}}\frac{{\partial A}}{{\partial t}}}}{{1 + \Delta {{{\left( {\frac{{\partial A}}{{\partial t}}} \right)}}^{2}}}} + \Gamma \frac{{\partial A}}{{\partial t}} = 0, \\ \end{gathered} $
(5)
${{r}_{k}} = \sum\limits_s {{{a}_{{sk}}}} \int\limits_{BZ} {dp{\text{cos}}\left( {pk} \right)} \frac{{{\text{exp}}\left( { - {{{{\varepsilon }_{s}}\left( p \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{s}}\left( p \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}}{{{\text{exp}}\left( { - {{{{\varepsilon }_{s}}\left( p \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{s}}\left( p \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right) + 1}},$
n0 – концентрация электронов, η определяет вектор смещений среды, kB – постоянная Больцмана, T – температура, ask – коэффициенты в разложении закона дисперсии электронов (3) в ряд Фурье:

(6)
${{\varepsilon }_{s}}\left( p \right) = \frac{1}{{2\pi }}\sum\limits_{s = 1}^m {\sum\limits_{k = 1}^\infty {{{a}_{{sk}}}{\text{cos}}\left( {pk} \right)} } ,$
(7)
${{a}_{{sk}}} = \int\limits_{BZ} {dp{\text{cos}}\left( {pk} \right){{\varepsilon }_{s}}\left( p \right)} ,$
(8)
$f\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {0,\,\,\,\,t < {{t}_{0}}\left( y \right)} \\ {\exp \left( { - \frac{t}{{{{t}_{{rel}}}}}} \right),\,\,\,\,t \geqslant {{t}_{0}}\left( y \right)} \end{array}} \right.,$

${{t}_{0}}\left( y \right) \cong {{\left( {y - {{y}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {y - {{y}_{0}}} \right)} \upsilon }} \right. \kern-0em} \upsilon }$ – момент времени, в который интенсивность импульса на его переднем фронте, измеренная в точке с координатой y, в е раз меньше пиковой интенсивности импульса; y0 – начальная координата “центра масс” импульса в начальный момент времени t = 0, $\upsilon \cong {c \mathord{\left/ {\vphantom {c {\sqrt {{{k}_{0}}} }}} \right. \kern-0em} {\sqrt {{{k}_{0}}} }}$ – аппроксимация скорости импульса по порядку величины, k0 – усредненная относительная диэлектрическая проницаемость среды (массива нанотрубок), trel – время релаксации электронной подсистемы УНТ [11].

Отметим, что вследствие убывания коэффициентов rk с ростом k в сумме можно ограничиться первыми нескольким неисчезающими слагаемыми [7], и получить широко применяемое в приложениях обобщенное уравнение sine–Gordon.

Величина η в (4) связана с ненулевой компонентой вектора смещений среды u как [17]:

(9)
$\eta = - сd\int\limits_{ - \infty }^t {\frac{{\partial u(y,t{\kern 1pt} ')}}{{\partial y}}dt{\kern 1pt} '} ,$
где d – пьезомодуль. Здесь, мы рассматриваем самую простую модель, когда в среде возникает поляризация линейная по приложенному электрическому полю и направленная параллельно этому электрическому полю вследствие пьезоэффекта: $P = d{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial z}}} \right. \kern-0em} {\partial z}}.$

Уравнение (9) в этом случае необходимо дополнить уравнением на ненулевую компоненту вектора смещений [18]:

(10)
$\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} + \gamma \frac{{\partial u}}{{\partial t}} + \omega _{0}^{2}u = \chi \frac{{\partial A}}{{\partial t}},$

здесь γ – коэффициент поглощения на ядрах среды (тяжелых ионах), ω0 – резонансная частота колебаний тяжелых ионов χ – коэффициент восприимчивости [19].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Исследуемые уравнения (4), (10) решались численно. Начальные условия для импульса выбирались следующим образом:

(11)
$\begin{gathered} A\left( {x,y,0} \right) = Q{\text{exp}}\left( { - \frac{{{{{\left( {x - {{x}_{0}}} \right)}}^{2}}}}{{l_{x}^{2}}}} \right){\text{exp}}\left( { - \frac{{{{{\left( {y - {{y}_{0}}} \right)}}^{2}}}}{{l_{y}^{2}}}} \right), \\ \frac{{dA\left( {x,y{\text{,0}}} \right)}}{{dt}} = \frac{{2Q\upsilon \left( {y - {{y}_{0}}} \right)}}{{l_{y}^{2}}}{\text{exp}}\left( { - \frac{{{{{\left( {x - {{x}_{0}}} \right)}}^{2}}}}{{l_{x}^{2}}}} \right) \times \\ \times \,\,{\text{exp}}\left( { - \frac{{{{{\left( {y - {{y}_{0}}} \right)}}^{2}}}}{{l_{y}^{2}}}} \right),\,\,\,\,u\left( {x,y{\text{,0}}} \right) = 0,\,\,\,\frac{{du\left( {x,y{\text{,0}}} \right)}}{{dt}} = 0, \\ \end{gathered} $
где Q – начальная амплитуда импульса, υ – начальная скорость импульса, lx, ly определяют ширину импульса вдоль направлений x и y соответственно, (x0, y0) – начальные координаты центра импульса.

Возникающая эволюция двумерного импульса при его распространении в массиве УНТ представлена на рис. 1. Импульс стабильно распространяется в среде с углеродными нанотрубками, испытывая незначительное уширение с течением времени.

Рис. 1.

Эволюция импульса (интенсивность электромагнитного поля $I = {{c}^{{ - 2}}}{{\left( {{{\partial A} \mathord{\left/ {\vphantom {{\partial A} {\partial t}}} \right. \kern-0em} {\partial t}}} \right)}^{2}}$ в единицах I0, I0 – максимум интенсивности при t = 0) при Φ/Φ0 = m/2: a) t = 0; б) t = 3.5 · 10–14 с; в) t = 6.5 · 10–14 с; г) t = 9.5 · 10–14 с. Единица по осям x и y соответствует 2 · 10–5 м.

Зависимость формы импульса от коэффициентов нелинейного поглощения и нелинейного поглощения с насыщением приведена на рис. 2. Видно, что энергия импульса при F1 ≠ 0, F2 ≠ 0 (кривые b и c) существенно меньше, чем в случае, когда нелинейное поглощение отсутствует (кривая a). При этом оба фактора (нелинейного F1 и насыщающегося поглощения F2 приводят к диссипации энергии, а также к сглаживанию “хвоста”, следующего за импульсом.

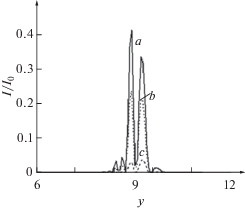
Рис. 2.

Зависимость интенсивности поля импульса I/I0, I0 – максимум интенсивности для разных значений коэффициентов нелинейного поглощения при t = 9.5 · 10–14 с, Φ/Φ0 = m/2 (построены продольные срезы при x = 0): (a) F1 = 0, F2 = 0; (b) F1 = 0.01, F2 = = 0.01; (c) F1 = 0.1, F2 = 0.1. Единица по оси и y соответствует 2 · 10–5 м.

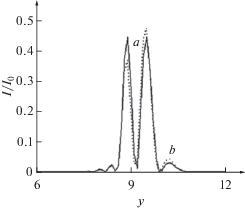
Влияние величины магнитного поля представлено на рис. 3. Из приведенных зависимостей видно, что влияние магнитного поля проявляется в перераспределении энергии импульса между двумя его основными пиками, область локализации импульса при этом сохраняется.

Рис. 3.

Зависимость интенсивности поля импульса I/I0, I0 – максимум интенсивности для разных значений величины магнитного потока при t = 9.5 · 10–14 с, F1 = 0.1, F2 = 0.1 (построены продольные срезы при x = 0): (a) Φ/Φ0 = 0 (магнитное поле отсутствует); (b) Φ/Φ0 = m/2. Единица по оси и y соответствует 2 · 10–5 м.

ЗАКЛЮЧЕНИЕ

Продемонстрировано стабильное распространение импульса под действием внешнего магнитного поля с учетом нелинейного и насыщающегося поглощения в углеродных нанотрубках. Показано, что учет нелинейного поглощения позволяет установить возможность эффективной компенсации усиления и создать стабильные условия для распространения импульса.

Авторы выражают благодарность Министерству науки и высшего образования РФ в рамках государственного задания за поддержку численного моделирования и параллельных вычислений (проект № 0633-2020-0003).

Список литературы

  1. Goorjian P.M. Photonic switching devices using light bullets. US Patent № 5651079. 1997.

  2. Xu L., Nishimura K., Fu Y. et al. // Opt. Expr. 2020. V. 28. № 10. Art. № 15138.

  3. Tsibidis G.D., Mouchliadis L., Pedio M. et al. // Phys. Rev. B. 2020. V. 101. Art. № 075207.

  4. Ахманов С.А., Выслоух В.А., Чиркин А.С. Оптика фемтосекундных лазерных импульсов. М: Наука, 1988. 309 с.

  5. Island J.O., Kissin P., Schalch J. et al. // Appl. Phys. Lett. 2020. V. 116. Art. № 161104.

  6. Dresselhaus M.S., Dresselhaus G., Eklund P.C. Science of fullerenes and carbon nanotubes. San Diego: Academic Press, 1996. 965 p.

  7. Belonenko M.B, Demushkina E.V., Lebedev N.G. // J. Rus. Laser Res. 2006. V. 27. P. 457.

  8. Белоненко М.Б., Лебедев Н.Г., Попов А.С. // Письма в ЖЭТФ. Т. 91. № 9. С. 506; Belonenko M.B., Lebedev N.G., Popov A.S. // JETP Lett. 2010. V. 91. № 9. P. 461.

  9. Zhukov A.V., Bouffanais R., Malomed B. et al. // Phys. Rev. A. 2016. V. 94. Art. № 053823.

  10. Yanyushkina N.N., Belonenko M.B., Lebedev N.G. et al. // Int. J. Mod. Phys. B. 2011. V. 25. P. 3401.

  11. Konobeeva N.N., Fedorov E.G., Rosanov N.N. et al. // J. Appl. Phys. V. 126. Art. № 203103.

  12. Konobeeva N., Belonenko M. // EPJ Web Conf. 2017. V. 161. Art. № 02012.

  13. Kamaraju N., Kumar S., Sood A.K. // Appl. Phys. Lett. 2007. V. 91. Art. № 251103.

  14. Zhukov A.V., Bouffanais R., Fedorov E.G. et al. // J. Appl. Phys. 2013. V. 114. Art. № 143106.

  15. Елецкий А.В. // УФН. 1997. Т. 167. № 9. С. 945; Eletskii A.V. // Phys. Usp. 1997. V. 40. № 9. P. 899.

  16. Овчинников А.А., Атражев В.В. // ФТТ. 1998. Т. 40. № 10. С. 1950; Ovchinnikov A.A., Atrazhev V.V. // Phys. Sol. St. 1998. V. 40. P. 1769.

  17. Ландау Л.Д., Лифшиц Е.М. Теория упругости. М.: Наука, 1987. 248 с.

  18. Блинц Р., Жекш Б. Сегнетоэлектрики и антисегнетоэлектрики. М.: Мир, 1975. 398 с.

  19. Конобеева Н.Н., Белоненко М.Б. // Опт. и спектроск. 2018. Т. 125. № 9. С. 391; Konobeeva N.N., Belonenko M.B. // Opt. Spectrosс. 2018. V. 125. № 9. P. 405.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал