1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 2, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 2, стр. 192-197

Искривление доменной границы при наличии наклонной симметричной магнитной неоднородности в пленочных материалах с большой анизотропией

М. Л. Акимов 1, *, П. А. Поляков 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”, физический факультет
Москва, Россия

* E-mail: ml.akimov@physics.msu.ru

Поступила в редакцию 30.08.2019
После доработки 16.09.2019
Принята к публикации 28.10.2019

Полный текст (PDF)

Аннотация

Разработана теория магнитного доменного упорядочения в магнитных пленочных материалах при наличии наклонной симметрично расположенной магнитной неоднородности в полосовом домене с учетом изменения магнитостатической энергии и изменения энергии анизотропии искривленной доменной границы.

Магнитные пленочные материалы имеют широкое применение в устройствах микроэлектроники и наноэлектроники, это обусловлено возникновением коллективного спинового упорядочения – важной особенностью магнитных систем, определяющей многие закономерности ее поведения. В магнитных системах возможно возникновение доменного упорядочения разного вида, например, спиральные домены, полосовые или лабиринтные домены, цилиндрические магнитные домены. Теория доменных структур в идеальных материалах была разработана, например, в [1–4]. Однако в реальных материалах существуют различные дефекты, которые приводят к искажению идеального магнитного упорядочения и, как следствие, к изменению макроскопических магнитных характеристик. На реализацию доменной структуры в равновесных состояниях в реальных условиях оказывают влияние существующие в ферромагнетике неоднородности и дефекты [1‒4] магнитного и немагнитного происхождения: примеси, пустоты, дефекты атомной структуры, форма поверхности образца и пр. Различные неоднородности в доменной структуре магнитной пленки могут быть получены статическими и динамическими методами [5, 6]. Смешанная доменная структура, состоящая из полосового домена и цилиндрического или эллиптического магнитного домена, представляет собой только одну из возможных сложных доменных структур [6–10]. В работах [6, 9] показана (экспериментально и теоретически) возможность существования квазиравновесной смешанной доменной структуры, представляющей собой систему полосовых доменов и цилиндрического или эллиптического магнитного домена, причем эта структура устойчива и может существовать бесконечно долго. Построенная аналитическая теория, описывающая данную смешанную структуру, хорошо согласуется с экспериментальными результатами, приведенными в этих работах. В работах [4–10] была построена теория магнитных доменных структур при наличии в магнитном пленочном материале магнитных неоднородностей. В [5] разработана модель магнитных доменных структур при несимметричном точечном дефекте дипольного типа с учетом только изменения магнитостатической энергии, обусловленной искривлением полосовой доменной структуры. В [11] разработана общая теория магнитного доменного упорядочения в магнитных пленочных материалах, при наличии симметрично расположенных цилиндрических магнитных неоднородностей с учетом изменений магнитостатической энергии и энергии анизотропии искривленной доменной границы. В результате искривления домена изменяется его площадь, и, следовательно, изменяется энергия доменной стенки, которая обусловлена анизотропией и обменным взаимодействием. В работе [11] исследуется влияние этого фактора на квазиравновесную смешанную доменную структуру, результаты проведенных исследований в работе [11] показывают, что влияние этого фактора при определенных параметрах может быть существенным. Проведен анализ влияния параметров, определяющих изменение энергии магнитостатического взаимодействия доменной структуры и энергии анизотропии искривленной доменной границы на форму и величину изгиба доменной границы. В [12] разработана общая теория магнитного доменного упорядочения в магнитных пленочных материалах при наличии несимметрично расположенной цилиндрической магнитной неоднородности с учетом изменений магнитостатической энергии и энергии анизотропии искривленной доменной границы. В [11, 12] разработана общая теория магнитного доменного упорядочения в магнитных пленочных материалах при наличии магнитных неоднородностей, вызванных цилиндрическим магнитным доменом, с учетом изменения магнитостатической энергии и энергии анизотропии искривленной доменной границы.

В данной работе построена теория магнитного доменного упорядочения в магнитных пленочных материалах при наличии наклонных магнитных неоднородностей, вызванных цилиндрическим магнитным доменом, симметрично расположенным в полосовом домене, с учетом изменений магнитостатической энергии и энергии анизотропии искривленной доменной границы.

Рассмотрим единичный изолированный полосовой домен с находлящейся внутри него наклонной цилиндрической магнитной неоднородности радиуса R. На рис. 1 изображен изолированный полосовой домен шириной w = 2a, расположенный вдоль координатной оси x в бесконечной пленке толщиной h. Координатная ось z направлена перпендикулярно плоскости пленки, а ось y – перпендикулярно доменной стенке. Начало системы координат помещено в центр цилиндрической магнитной неоднородности. Магнитостатическое поле рассеяния данной цилиндрической магнитной неоднородности исказит форму полосового домена и приведет к зависимости его ширины от координаты x.

Рис. 1.

Наклонный цилиндрический магнитный домен в полосовом домене.

На рис. 2 изображена схема, показывающая расположение наклонных смещенных магнитных зарядов цилиндрической неоднородности, находящихся внутри полосового домена. Точки M и N – центры круговых оснований цилиндрического дефекта, $\Delta $ – расстояние между точками M и N, соответствующими центрам наклонных магнитных зарядов ($\Delta $ – параметр наклона цилиндрической магнитной неоднородности).

Рис. 2.

Схема расположения наклонной цилиндрической неоднородности.

Если функция $y\left( x \right)$ описывает изгиб доменной стенки полосового домена, то изменение магнитной энергии, рассматриваемое как функционал от неизвестной функции $y\left( x \right),$ можно представить в виде:

(1)
$W = {{W}_{1}} + {{W}_{2}} + {{W}_{3}} + {{W}_{4}} + {{W}_{5}} + {{W}_{6}}.$

Рассмотрим члены этого функционала

$\begin{gathered} {{W}_{1}} = - 8{{\sigma }^{2}}\int\limits_{ - A}^A {dx} \int\limits_a^{y(x)} {dy} \int\limits_{ - A}^A {dx{\kern 1pt} '} \int\limits_{y(x{\kern 1pt} ')}^b {dy{\kern 1pt} '} \frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}} }} - \frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}} + {{h}^{2}}} }} \\ - \,\,8{{\sigma }^{2}}\int\limits_{ - A}^A {dx} \int\limits_a^{y(x)} {dy} \int\limits_{ - A}^A {dx{\kern 1pt} '} \int\limits_{ - b}^{ - y(x{\kern 1pt} ')} {dy{\kern 1pt} '} \frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}} }} - \frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}} + {{h}^{2}}} }} \\ \end{gathered} $

– изменение магнитостатической энергии, обусловленное искривлением доменных границ в двух прямолинейных полосах, обрамляющих изогнутые доменные границы и параллельных оси x, а также изменение энергии взаимодействия магнитных зарядов между поверхностными зарядами выделенных полос, обусловленное искривлением доменных границ. Здесь b – значение функции y(x) при х = 0, описывающей форму искажения доменной границы полосового домена вследствие магнитостатического поля рассеяния цилиндрического домена, σ – поверхностная плотность магнитостатических зарядов, равная нормальной составляющей вектора намагниченности, A – параметр регуляризации.

$\begin{gathered} {{W}_{2}} = - 2{{\sigma }^{2}}\int\limits_{ - R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} \int\limits_{ - A}^A {dx} \int\limits_a^{y(x)} {dy} \left[ {\left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }} - } \right.} \right. \\ \left. { - \,\,\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right) - \int\limits_{ - A}^A {dx} \int\limits_{y(x)}^b {dy} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }} - } \right. \\ \left. {\left. { - \,\,\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right)} \right] - 2{{\sigma }^{2}}\int\limits_{ - R + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} \int\limits_{ - A}^A {dx} \int\limits_a^{y(x)} {dy} \left[ {\left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }} - } \right.} \right. \\ \left. { - \,\,\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right) - \int\limits_{ - A}^A {dx} \int\limits_{y(x)}^b {dy} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }}} \right. - \left. {\left. {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right)} \right] \\ \end{gathered} $

– энергия взаимодействия наклонных магнитных зарядов цилиндрического домена или дефекта с наведенными за счет изгиба доменных границ поверхностными магнитными зарядами полосового домена.

$\begin{gathered} {{W}_{3}} = 4{{\sigma }^{2}}\int\limits_{ - A}^A {dx} \int\limits_{ - a}^a {dy} \int\limits_{ - A}^A {dx{\kern 1pt} '} \int\limits_a^{y(x{\kern 1pt} ')} {dy{\kern 1pt} '} \left( {\frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}} }}} \right. - \left. {\frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}} + {{h}^{2}}} }}} \right) + \\ + \,\,4{{\sigma }^{2}}\int\limits_{ - A}^A {dx} \int\limits_{ - a}^a {dy} \int\limits_{ - A}^A {dx{\kern 1pt} '} \int\limits_{ - y(x{\kern 1pt} ')}^{ - a} {dy{\kern 1pt} '} \left( {\frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}} }}} \right. - \left. {\frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}} + {{h}^{2}}} }}} \right) - \\ - 8{{\sigma }^{2}}\int\limits_{ - A}^A {dx} \int\limits_b^B {dy} \int\limits_{ - A}^A {dx{\kern 1pt} '} \int\limits_a^{y(x{\kern 1pt} ')} {dy{\kern 1pt} '} \left( {\frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}} }}} \right. - \left. {\frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}} + {{h}^{2}}} }}} \right) - \\ - \,\,8{{\sigma }^{2}}\int\limits_{ - A}^A {dx} \int\limits_{ - B}^{ - b} {dy} \int\limits_{ - A}^A {dx{\kern 1pt} '} \int\limits_a^{y(x{\kern 1pt} ')} {dy{\kern 1pt} '} \left( {\frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}} }}} \right. - \left. {\frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}} + {{h}^{2}}} }}} \right) \\ \end{gathered} $

– изменение магнитостатической энергии взаимодействия верхней и нижней поверхностей не искривленного полосового домена с прилегающими к ним параллельны оси x прямолинейными полосками, обрамляющими изогнутые доменные границы, а также изменение энергии взаимодействия прямолинейных полубесконечных плоскостей, с полосками, обрамляющими изогнутые доменные границы полосового домена, где B – параметр регуляризации.

$\begin{gathered} {{W}_{4}} = 2\mathop \sigma \nolimits^2 \int\limits_{ - R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} \left[ {2\int\limits_{ - A}^A {dx} \int\limits_b^B {dy} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }}} \right.} \right. - \left. {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right) - \\ - \,\,\int\limits_{ - A}^{ - R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {dx} \int\limits_{ - a}^a {dy} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }}} \right. - \left. {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right) - \\ - \,\,\int\limits_{ - R}^R {dx} \int\limits_{ - a}^{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {dy} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }}} \right. - \left. {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right) - \\ - \,\,\int\limits_{ - R}^R {dx} \int\limits_{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^a {dy} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }} - } \right.\left. {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right) - \\ - \,\,\int\limits_{R - \Delta {\text{/}}2}^A {dx} \int\limits_{ - a}^a {dy} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}}} }}} \right. - \left. {\left. {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right)} \right] \\ \end{gathered} $

– энергия взаимодействия наклонных магнитных зарядов цилиндрического домена с поверхностными зарядами верхней и нижней частей не искривленного полосового домена и с полубесконечными плоскостями, ограничивающими изолированный полосовой домен в магнитной пленке.

${{W}_{5}} = 2\sigma h{{H}_{z}}\int\limits_{ - A}^A {dx} \int\limits_{ - y\left( x \right)}^{ - a} {dy} + 2\sigma h{{H}_{z}}\int\limits_{ - A}^A {dx} \int\limits_a^{y\left( x \right)} {dy + {\text{const}}} $

– изменение магнитостатической энергии полосового домена во внешнем магнитном поле смещения, где Hz – магнитное поле, параллельное оси z, const – члены, не зависящие от изгиба доменной границы.

${{W}_{6}} = 2h\alpha \int\limits_{ - A}^A {\left( {\sqrt {1 + {{{\left( {\frac{{dy}}{{dx}}} \right)}}^{2}}} - 1} \right)} dx$

– изменение энергии анизотропии искривленной доменной границы, где $\alpha = 4\sqrt {\tilde {А}K} ,$ K – константа кристаллической анизотропии, $\tilde {А}$ – обменная константа.

Вычисляя вариационную производную функционала изменения магнитной энергии (1) и приравнивая ее нулю, получаем нелинейное функциональное интегральное уравнение для функции y(x), которое при относительно малых искривлениях доменных границ можно линеаризовать. Раскладывая функцию y(x) в пределах интегрирования в ряд относительно точек $a$ и $b,$ имеем уравнение:

(2)
$\begin{gathered} \int\limits_{ - A}^A {dx{\kern 1pt} '\left[ {{{P}_{1}}\left( {x{\kern 1pt} '} \right) + {{P}_{2}}\left( {x{\kern 1pt} '} \right)} \right]\left( {y\left( {x{\kern 1pt} '} \right) - a} \right)} - \\ - \,\,\left( {y\left( {x{\kern 1pt} '} \right) - a} \right)f + 4\frac{{ha}}{{{{\sigma }^{2}}}}\left( {y\left( {x{\kern 1pt} '} \right) - a} \right)\frac{{{{d}^{2}}y}}{{d{{x}^{2}}}} = \\ = \,\,\frac{1}{2}\int\limits_{ - R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}}} }} - } \right. \\ - \,\,\left. {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right) + \\ + \,\,\frac{1}{2}\int\limits_{ - R + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} \left( {\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}}} }} - } \right. \\ \left. { - \,\,\frac{1}{{\sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right), \\ \end{gathered} $
где $\psi = b - a,$ $\nu = b + a,$ $f = 4\ln \left[ {1 + \frac{{{{h}^{2}}}}{{4{{a}^{2}}}}} \right],$

${{P}_{1}}\left( {x{\kern 1pt} '} \right) = \frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{\psi }^{2}}} }} - \frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{\psi }^{2}} + {{h}^{2}}} }},$
${{P}_{2}}\left( {x{\kern 1pt} '} \right) = \frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{\nu }^{2}}} }} - \frac{1}{{\sqrt {{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{\nu }^{2}} + {{h}^{2}}} }}.$

Уравнение (2) является линейным интегральным уравнением типа свертки, и может быть решено методом преобразования Фурье [13, 14]. Проводя косинус-преобразование Фурье уравнения (2), получим:

(3)
$\begin{gathered} \left\{ {{{K}_{0}}\left( {y\psi } \right) - {{K}_{0}}\left( {y\sqrt {{{\psi }^{2}} + {{h}^{2}}} } \right) + {{K}_{0}}\left( {y\nu } \right) - } \right. \\ \left. { - \,\,{{K}_{0}}\left( {y\sqrt {{{\nu }^{2}} + {{h}^{2}}} } \right) + f + \frac{{h\alpha {{y}^{2}}}}{{{{\sigma }^{2}}}}} \right\}\left( {y\left( {x{\kern 1pt} '} \right) - a} \right) = \\ = \frac{1}{2}\int\limits_0^\infty {dx{\kern 1pt} '} \int\limits_{ - R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} \left( {\frac{1}{{\sqrt {{{{\left( {x{\kern 1pt} ' - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}}} }} - } \right. \\ - \,\,\left. {\frac{1}{{\sqrt {{{{\left( {x{\kern 1pt} ' - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right)\cos \left( {x{\kern 1pt} 'y} \right)\,\,\, + \\ + \,\,\frac{1}{2}\int\limits_0^\infty {dx{\kern 1pt} '} \int\limits_{ - R + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} \times \\ \times \,\,\left( {\frac{1}{{\sqrt {{{{\left( {x{\kern 1pt} ' - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}}} }} - } \right.\left. {\frac{1}{{\sqrt {{{{\left( {x{\kern 1pt} ' - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}} \right)\cos \left( {x{\kern 1pt} 'y} \right), \\ \end{gathered} $
где $\left( {\tilde {y}\left( x \right) - a} \right)$ – фурье-образ функции $\left( {y\left( x \right) - a} \right)$, K0(γ) – функция Макдональда [14].

Решая уравнение (3) и выполняя обратное преобразование Фурье, для функции y(x), описывающей искривление доменной границы полосового домена вследствие воздействия магнитостатического поля рассеяния цилиндрического домена, получим следующие выражение:

(4)
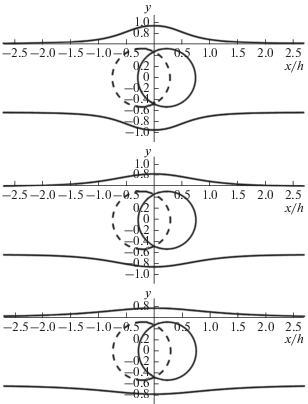
$y\left( x \right) = a + \sqrt {\tfrac{2}{\pi }} \,\int\limits_0^\infty {\tfrac{{N{\text{(}}y{\text{)}}\cos {\text{(}}xy{\text{)}}dy}}{{{{K}_{0}}\left( {y\psi } \right) - {{K}_{0}}\left( {y\sqrt {{{\psi }^{2}} + {{h}^{2}}} } \right) + {{K}_{0}}\left( {y\nu } \right) - {{K}_{0}}\left( {y\sqrt {{{\nu }^{2}} + {{h}^{2}}} } \right) + f + \frac{{h\alpha {{y}^{2}}}}{{{{\sigma }^{2}}}}}}} ,$
где

$\begin{gathered} N\left( y \right) = \frac{1}{2}\int\limits_0^\infty {dx{\kern 1pt} '} \int\limits_{ - R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} \times \\ \times \,\,P\left( {x{\kern 1pt} ',{{x}_{1}},{{x}_{2}}} \right)\cos \left( {x{\kern 1pt} 'y} \right) + \frac{1}{2}\int\limits_0^\infty {dx{\kern 1pt} '} \int\limits_{ - R + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}}^{R + {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} {d{{x}_{1}}} \int\limits_{ - \sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} }^{\sqrt {{{R}^{2}} - {{{\left( {{{x}_{1}} - {\Delta \mathord{\left/ {\vphantom {\Delta 2}} \right. \kern-0em} 2}} \right)}}^{2}}} } {d{{x}_{2}}} P\left( {x{\kern 1pt} ',{{x}_{1}},{{x}_{2}}} \right)\cos \left( {x{\kern 1pt} 'y} \right), \\ P\left( {x{\kern 1pt} ',{{x}_{1}},{{x}_{2}}} \right) = \frac{1}{{\sqrt {{{{\left( {x{\kern 1pt} ' - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}}} }} - \frac{1}{{\sqrt {{{{\left( {x{\kern 1pt} ' - {{x}_{1}}} \right)}}^{2}} + {{{\left( {a - {{x}_{2}}} \right)}}^{2}} + {{h}^{2}}} }}. \\ \end{gathered} $

Проведено сравнение теоретических кривых форм изгиба доменной границы, вычисленных на основании приведенной выше теории полосового домена, в зависимости от параметра $Q = \frac{{\pi \sqrt {\tilde {А}K} }}{{2{{\sigma }^{2}}h}},$ определяющего величину изменения энергии анизотропии искривленной доменной границы. Теоретический расчет величин максимальных изгибов доменных границ полосового домена ($b$ – a, где a – полуширина полосового домена, $b$ – максимальное значение функции $y\left( x \right)$ при х = 0) по формуле (4), рис. 3, при геометрических параметрах тонкой пленки, взятых из эксперимента [6, 10] (w = 16 мкм – ширина полосового домена, h = 13 мкм – толщина магнитной пленки, R = 6.75 мкм – средний радиус области, моделирующей воздействие, наклонного цилиндрического магнитного домена; $\Delta $ = 6 мкм (параметр наклона цилиндрической магнитной неоднородности), а при Q = 0 имеет значение 4.1 мкм. При увеличении величины изменения энергии анизотропии искривленной доменной границы (увеличение параметра Q) наблюдается уменьшение величины изгиба доменной границы полосового домена, обусловленное влиянием поля рассеяния наклонной цилиндрической магнитной неоднородности (4.1 мкм при Q = 0; 2.87 мкм при Q = 0.2; 2.0 мкм при Q = 0.8) и уширение изгиба доменной границы (см. рис. 3). Также возможен случай, когда изменение энергии анизотропии искривленной доменной границы будет существенно преобладать над изменением магнитостатической энергии, обусловленным искривлением доменных границ, что будет приводить к подавлению искривления доменной границы полосового домена, обусловленного влиянием магнитостатического поля рассеяния цилиндрического магнитного домена.

Рис. 3.

Форма доменных границ при параметрах: Q = 0; Q = 0.2; Q = 0.8 (сверху вниз), h = 13 мкм – толщина магнитной пленки.

Список литературы

  1. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1992. 664 с.

  2. Вонсовский С.В. Магнетизм. М.: Наука, 1971. 1032 с.

  3. Kittel Ch. // Rev. Mod. Phys. 1949. V. 21. P. 541.

  4. Эшенфельдер А. Физика и техника цилиндрических магнитных доменов. М.: Мир, 1983. 496 с.

  5. Akimov M.L., Boltasova Yu.V., Polyakov P.A. // J. Comm. Tech. Electron. 2001. V. 46. P. 469.

  6. Акимов М.Л., Поляков П.А., Усманов Н.Н. // ЖЭТФ. 2002. Т. 121. № 2. С. 347; Akimov M.L., Polyakov P.A., Usmanov N.N. // JETP. 2002. V. 94. № 2. P. 293.

  7. Akimov M.L., Polyakov P.A. // Moscow Univ. Phys. Bull. 2004. V. 59. № 2. P. 53.

  8. Акимов М.Л., Вагин Д.В., Поляков О.П. и др. // Изв. РАН. Сер. физ. 2007. Т. 71. № 11. С. 1599; Akimov M.L., Vagin D.V., Polyakov O.P. et al. // Bull. Russ. Acad. Sci. Phys. 2007. V. 71. № 11. P. 1556.

  9. Akimov M.L., Polyakov P.A., Starokurov Y.V. et al. // Physica B. 2010. V. 405. P. 2376.

  10. Akimov M.L., Polyakov P.A., Banishev A.A. et al. // Int. J. Mod. Phys. B. 2016. V. 30. № 12. Art. № 1650081.

  11. Akimov M.L., Polyakov P.A., Rusakova N.E. // Int. J. Mod. Phys. B. 2018. V. 32. № 1. Art. № 1750272.

  12. Акимов М.Л., Поляков П.А. // Изв. РАН. Сер. физ. 2018. Т. 82. № 8. С. 1070; Akimov M.L., Polyakov P.A. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. № 8. P. 968.

  13. Бейтмен Г., Эрдейи А. Таблица интегральных преобразований. М.: Наука, 1969. 343 с.

  14. Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979. 830 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал