Известия РАН. Серия физическая, 2020, T. 84, № 2, стр. 247-250

ВВЕДЕНИЕ

Проблема повышения эффективности взаимодействия электронных пучков большой мощности с электромагнитным полем является актуальной для генераторов и усилителей релятивистской СВЧ-электроники вот уже на протяжении многих лет [1–3]. Среди предложенных способов ее решения для устройств черенковского типа обратим внимание на возможность оптимизации КПД энергообмена между частицами и высокочастотным полем за счет изменения величины постоянного однородного внешнего магнитного поля ${{\vec {B}}_{0}},$ служащего для транспортировки пучка через электродинамическую структуру прибора. Как было показано в [4], существует диапазон значений B₀, при которых пространственная длина области с высоким КПД значительно возрастает. Данный эффект объясняется особенностью динамики электронов, продольная скорость движения которых в процессе взаимодействия с замедленной волной сильно уменьшилась. Величина B₀ выбиралась такой, чтобы для этих частиц было выполнено условие циклотронного резонанса. В результате частицы, уже отдавшие свою энергию полю замедленной волны, приобретают значительную поперечную скорость и полностью выходят из фазового синхронизма с этой волной. Отметим, что в реальном эксперименте ${{\vec {B}}_{0}}$ создается либо соленоидом конечной длины, либо набором катушек с током, либо их комбинацией. Это означает, что существуют области пространства, где ведущее магнитное поле не будет однородным.

Исследование влияния таких неоднородностей на динамику электронов в системе, аналогичной рассмотренной в [4], и являлось целью данной работы.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим модельную задачу, в которой движение частиц трехмерно, а электромагнитное поле соответствует двумерному случаю. Такое приближение допустимо, если диаметр электродинамической структуры рассматриваемого прибора и кольцевого пучка много больше характерной длины волны, что выполняется, в частности, для многоволновых черенковских генераторов (МВЧГ).

Введем декартову систему координат, направление оси z которой совпадает с направлением распространения пучка заряженных частиц. Плоскость x = 0 соответствует поверхности электродинамической структуры.

Для моделирования энергообмена между пучком заряженных частиц и замедленной волной воспользуемся так называемым приближением заданного поля. А именно, будем считать, что амплитуда высокочастотного поля во всем пространстве взаимодействия не изменяется со временем. Такое предположение допустимо в случае, если в приборе уже установился процесс стационарной генерации. Влиянием пространственного заряда, создаваемого пучком, на динамику отдельных частиц пренебрежем.

Статическое магнитное поле в пространстве взаимодействия представим в виде суперпозиции однородного ведущего поля ${{\vec {B}}_{0}} = \left\{ {0,0,{{B}_{{0z}}}} \right\}$ и поля ${{\vec {B}}_{s}}(x,z)$ = $\left\{ {{{B}_{{sx}}}(x,z),0,{{B}_{{sz}}}(x,z)} \right\}$ набора стержней с током, лежащих в плоскости x = x_s < 0 и расположенных перпендикулярно силовым линиям ${{\vec {B}}_{0}}.$ Высокочастотное поле $\left( {{{{\vec {E}}}_{w}},{{{\vec {B}}}_{w}}} \right)$ соответствует полю замедленной волны и имеет три отличные от нуля компоненты: E_wx, E_wz, и B_wy. Частоту и коэффициент замедления волны выбирали по данным дисперсионной характеристики электродинамической структуры МВЧГ, которая была получена из решения нестационарной трехмерной задачи [5].

Таким образом, уравнения движения N заряженных частиц образуют следующую систему из 2N обыкновенных дифференциальных уравнений:

где e, m – заряд и масса электрона, c – скорость света в вакууме, ${{\vec {P}}_{i}},{{\vec {r}}_{i}}$ – импульс и координата i‑й частицы.

Исследование динамики частиц проводили численными методами. В виду того, что уравнение (1) нелинейно (неизвестное значение ${{\vec {P}}_{i}}$ входит и в левую, и в правую части) для решения системы (1), (2) был использован модифицированный метод “с перешагиванием”. Он основан на стандартном методе [6, 7], в котором при вычислении последующего значения неизвестной величины ${{\vec {P}}_{i}}({{t}^{n}} + \Delta t)$ (здесь $\Delta \,t$ – дискретный шаг по времени) правая часть берется в момент времени ${{t}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ сдвинутый относительно текущего на $\Delta t{\text{/2}},$ что позволяет получить разностную аппроксимацию второго порядка точности. В модифицированном методе для интегрирования (1), (2) используются две временные последовательности, сдвинутые друг относительно друга на $\Delta t{\text{/2}}.$ Рекуррентные соотношения этого метода для вычисления траектории i-й частицы, записанные в векторной форме, имеют следующий вид:

В (3)–(6) верхние индексы обозначают момент времени. Для всех составляющих электромагнитного поля эти индексы подразумевают следующее: ${{\vec {E}}^{{n + k}}} = \vec {E}\left( {r_{i}^{{n + k}},{{t}^{{n + k}}}} \right),$ ${{\vec {B}}^{{n + k}}} = \vec {B}\left( {r_{i}^{{n + k}}} \right).$

Начальные значения координат и импульсов частиц задаются в каждой временной последовательности отдельно, т.е. для ${{t}^{0}}\, = \,0$ и для ${{t}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} 2}} \right. \kern-0em} 2}$ соответственно.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Моделирование динамики было выполнено для различных конфигураций ${{\vec {B}}_{s}}(x,z),$ но во всех случаях изменение продольного статического поля за счет неоднородности не превышало 10%, т.е. ${{{{B}_{{sz}}}} \mathord{\left/ {\vphantom {{{{B}_{{sz}}}} {{{B}_{{0z}}}}}} \right. \kern-0em} {{{B}_{{0z}}}}} \leqslant 0.1.$ Как известно, из условия ${\text{div}}\vec {B} = 0$ следует, что если величина продольной составляющей изменяется в пространстве, то появляется соответствующая этому изменению поперечная компонента магнитного поля.

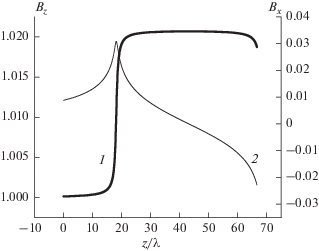
Приведенные ниже результаты моделирования были получены для случая, когда стержни с током располагались в интервале от 18λ до 68λ (через 1/3λ) по продольной координате и находились ниже плоскости, описывающей поверхность электродинамической структуры на 1/3λ (λ – характерная длина волны излучения МВЧГ). Постоянный ток имел одинаковое значение во всех стержнях. На рис. 1. приведены зависимости от координаты z продольной (кривая 1, левая шкала) и поперечной (кривая 2, правая шкала) компонент статического поля, нормированных на значение B₀.

Фазовая скорость волны была выбрана равной 0.9175с. Начальная скорость υ₀, соответствующая импульсу P₀, для всех частиц была одинаковой для одного вычислительного эксперимента. В проведенной серии экспериментов υ₀ варьировалась в диапазоне от 0.92с до 0.97с.

На рис. 2 приведены результаты моделирования для случая, когда υ₀ = 0.96 с. Траектории частиц в координатах “продольный импульс–продольная координата” изображены на рис. 2а. На входе в пространство взаимодействия электроны, попавшие в ускоряющую фазу замедленной волны, образуют группу 1. Частицы, скорость которых на входе получила отрицательное приращение, образуют группу 2. Именно эти электроны начинают эффективно отдавать свою энергию волне, в результате чего значение их продольного импульса существенно уменьшается. В данном случае минимальное значение P_z достигает 0.45 P₀ (z ~ 15λ). В то же время за счет наличия неоднородности статического магнитного поля электроны начинают отходить от поверхности электродинамической структуры, что иллюстрируют траектории частиц в координатах x и z (рис. 2б, 1, левая шкала). Так как амплитуда замедленной волны с увеличением x экспоненциально спадает, то и работа силы, совершаемая волной над электронами пучка, тоже уменьшается. За счет этого часть замедлившихся электронов образуют группу 3 (рис. 2а), и доля частиц, отдавших свою энергию полю, по отношению к общему количеству частиц пучка остается значительной. В результате пространственная область положительных значений КПД увеличивается (рис. 2б, кривая 2, правая шкала).

ЗАКЛЮЧЕНИЕ

Таким образом, в рассмотренном случае механизм увеличения положительной области эффективности взаимодействия η электронов пучка и поля замедленной волны отличается от описанного в [4]. А именно, даже малая по относительной величине неоднородность поперечной компоненты статического поля приводит к значительному поперечному смещению пучка. Направление смещения зависит от фазы СВЧ-волны, в которой находится частица. Это означает, что можно создать такую конфигурацию неоднородности ведущего поля, при которой частицы, отдавшие свою энергию замедленной волне, удаляются от поверхности электродинамической структуры и попадают в область малых значений амплитуд СВЧ-поля, т.е. в область малой связи с волной. Это, в свою очередь, будет приводить к увеличению пространственной области положительных значений КПД.

Моделирование было проведено на вычислительных ресурсах Межведомственного суперкомпьютерного центра РАН.