Известия РАН. Серия физическая, 2020, T. 84, № 2, стр. 254-257

Плазменные волны в двумерной сверхрешетке с неаддитивным энергетическим спектром в присутствии сильного статического электрического поля

С. Ю. Глазов^{1, 2, *}, А. А. Ковалев¹, С. В. Крючков^{1, 3}

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Волгоградский государственный социально-педагогический университет”
Волгоград, Россия

² Федеральное государственное бюджетное образовательное учреждение высшего образования “Волгоградский государственный медицинский университет”
Волгоград, Россия

³ Федеральное государственное бюджетное образовательное учреждение высшего образования “Волгоградский государственный технический университет”
Волгоград, Россия

^* E-mail: ser-glazov@yandex.ru

Поступила в редакцию 26.08.2019
После доработки 13.09.2019
Принята к публикации 28.10.2019

DOI: 10.31857/S036767652002012X

Полный текст (PDF)

Аннотация

Исследовано влияние неаддитивности энергетического спектра двумерной сверхрешетки (СР) на закон дисперсии плазменных волн в условиях воздействия сильного статического электрического поля. Расчеты выполнены на основе квантовой теории плазменных волн в приближении случайных фаз с учетом процессов переброса.

ВВЕДЕНИЕ

В последнее время внимание многих исследователей обращено к коллективным явлениям в низкоразмерных системах, в частности, к процессам распространения в них плазменных волн. Особый интерес в этой связи вызывают структуры на основе атома углерода: монослойный и двуслойный графен, углеродные нанотрубки, фуллерены. Данные объекты обладают огромным спектром необычных свойств и потенциально широкими возможностями их применения. Интерес к изучению плазменных возбуждений в структурах на основе графена объясняется их возможным применением в электронных приборах для детектирования и генерации электромагнитного излучения различных частотных диапазонов, в том числе терагерцового и инфракрасного [1]. Применение плазменных волн обусловлено значительно более высокими скоростями плазменных возбуждений по сравнению с дрейфовой скоростью электронов [2], которые примерно на два порядка превышают максимально достижимую дрейфовую скорость носителей. Это позволяет использовать плазмоны в качестве переносчиков электрических сигналов, что может повысить быстродействие электронных устройств.

Теоретическому исследованию закона дисперсии плазменных волн ω$\left( {\vec {k}} \right)$ в электронном 2D-газе одномерной графеновой СР посвящено достаточно большое количество работ [3–6]. В последнее время внимание исследователей сосредотачивается на изучении графеновых 2D-сверхрешеток (ГСР) [7–9]. В настоящей работе рассматриваются особенности законов дисперсии плазменных волн ω$\left( {\vec {k}} \right)$ в 2D-ГСР и узкозонной полупроводниковой 2D-СР, связанные с неаддитивностью их энергетических спектров.

ЭНЕРГЕТИЧЕСКИЙ СПЕКТР 2D-СВЕРХРЕШЕТОК

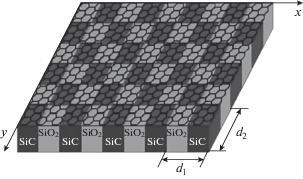
Энергетический спектр носителей заряда в 2D-ГСР на подложке, аналогичной шахматной доске (рис. 1) в одноминизонном приближении имеет вид [7]

(1)

$\varepsilon (\vec {p}) = \pm \sqrt {\Delta _{0}^{2} + \Delta _{1}^{2}\left( {1 - \cos ({{{{p}_{x}}{{d}_{1}}} \mathord{\left/ {\vphantom {{{{p}_{x}}{{d}_{1}}} \hbar }} \right. \kern-0em} \hbar })} \right) + \Delta _{2}^{2}\left( {1 - \cos ({{{{p}_{у}}{{d}_{2}}} \mathord{\left/ {\vphantom {{{{p}_{у}}{{d}_{2}}} \hbar }} \right. \kern-0em} \hbar })} \right)} ,$

где p_x, p_y − компоненты квазиимпульса электрона, d_i = a_i + b_i − период ГСР, i = {1, 2}, a_i и b_i − линейные размеры областей бесщелевого и щелевого графена. Разные знаки относятся к минизоне проводимости и валентной минизоне. Энергетический спектр ГСР неаддитивен, поэтому существует зависимость движения носителей заряда вдоль ортогональных направлений, и непараболичен, что определяет нелинейную зависимость скорости электрона от квазиимпульса. При малых p_y выражение (1) переходит в известное дисперсионное соотношение для одномерной ГСР на полосчатой подложке [10].

Рис. 1.

Двумерная графеновая сверхрешетка.

Аппроксимация зависимости энергетического спектра электронов первой минизоны проводимости от компоненты квазиимпульса p_|| вдоль оси ГСР выбрана в виде

(2)

${{\varepsilon }_{1}}({{p}_{{||}}},0) = {{\Delta }_{g}}\sqrt {{{f}_{1}}^{2} + {{f}_{2}}^{2}\left( {1 - \cos ({{{{p}_{{||}}}d} \mathord{\left/ {\vphantom {{{{p}_{{||}}}d} \hbar }} \right. \kern-0em} \hbar })} \right)} ,$

где Δ_g − полуширина запрещённой зоны щелевой модификации графена, коэффициенты f_i подбираются численно на основе непосредственного решения дисперсионного соотношения из [11]. Спектр (2) использовался для описания носителей в ГСР [3, 6, 8, 10], но известен еще раньше в теории узкозонных полупроводников и квантовых полупроводниковых сверхрешеток [12]. Для аналитических расчетов удобно использовать разложение (1) в двойной ряд Фурье. В работе [13] показано, что с увеличением периода ГСР уменьшается неаддитивность энергетического спектра и при d > 5 ⋅ 10^–6 см можно с хорошей степенью точности аппроксимировать “истинный” спектр структуры аддитивной зависимостью энергии от квазиимпульса. В данном случае увеличение периода ГСР будет приводить к более быстрому уменьшению значений коэффициентов разложения с ростом индексов.

Рассмотрим пример симметричной ГСР, когда d₁ = d₂ = d ≈ 2 ⋅ 10^–6 см, Δ₁= Δ₂ ≈ 0.332Δ_SiC, Δ_SiC = = 0.13 эВ, ширина запрещенной зоны между валентной зоной и зоной проводимости ε_g = = 0.8573Δ_SiC; ширина запрещенной зоны между первой и второй зонами проводимости ε_g12= = 0.6270Δ_SiC; ширина первой минизоны проводимости ε_e = 0.2111Δ_SiC. При разложении спектра в ряд Фурье в этом случае можно ограничиться первыми слагаемыми

(3)

$\begin{gathered} \varepsilon (\vec {p}) = {{\Delta }_{{{\text{SiC}}}}}\left\{ {{{g}_{1}} - \frac{{{{g}_{2}}}}{2}\left[ {\cos \left( {\frac{{{{p}_{x}}d}}{\hbar }} \right) + \cos \left( {\frac{{{{p}_{у}}d}}{\hbar }} \right)} \right] - } \right. \\ \left. { - \,\,{{g}_{3}}\cos \left( {\frac{{{{p}_{x}}d}}{\hbar }} \right)\cos \left( {\frac{{{{p}_{у}}d}}{\hbar }} \right)} \right\}, \\ \end{gathered} $

где g₁ = 0.624475, g₂ = 0.1787, g₃ = 0.01306. Для рассматриваемого примера максимальное расхождение спектров составляет 2%.

ОСНОВНЫЕ УРАВНЕНИЯ

На основе квантовой теории плазменных волн в приближении случайных фаз с учетом процессов переброса получено выражение для нахождения закона дисперсии плазменных волн в электронном 2D-газе ГСР в присутствии сильного (Ω_st $ \gg $ ω) постоянного электрического поля, приложенного вдоль оси x:

(4)

$\frac{{2\pi {{e}^{2}}}}{\chi }\left( {\Pi (\vec {k},\omega ) - \Pi (\vec {k},\omega ,\xi )} \right)S(\vec {k}) = 1,$

где $\Pi (\vec {k},\omega ,\gamma )$ = $J_{0}^{2}\left( {\frac{\Delta }{{\hbar {{\Omega }_{{st}}}}}\sin ({{{{k}_{x}}d} \mathord{\left/ {\vphantom {{{{k}_{x}}d} 2}} \right. \kern-0em} 2})} \right)$ × × $\sum\nolimits_{\vec {p}} {\gamma \frac{{n(\vec {p} + \vec {k}) - n(\vec {p})}}{{\varepsilon ({{p}_{y}} + {{k}_{y}}) - \varepsilon ({{p}_{y}}) - \hbar \omega }}} ,$ $\Pi (\vec {k},\omega )$ = $\Pi (\vec {k},\omega ,1),$ $\xi = {{({\delta \mathord{\left/ {\vphantom {\delta {2\hbar {{\Omega }_{{st}}}}}} \right. \kern-0em} {2\hbar {{\Omega }_{{st}}}}})}^{2}}$$\left[ {1 - \cos ({{k}_{y}}d)} \right.$(1 – 2cos²$\left( {{{{{p}_{y}}d} \mathord{\left/ {\vphantom {{{{p}_{y}}d} \hbar }} \right. \kern-0em} \hbar } + } \right.$ + $\left. {\left. {\left. {{{{{k}_{y}}d} \mathord{\left/ {\vphantom {{{{k}_{y}}d} 2}} \right. \kern-0em} 2}} \right)} \right)} \right],$

Δ = g₂Δ_SiC, δ = g₃Δ_SiC, χ – диэлектрическая проницаемость, Ω_st = eEd/$\hbar $ – штарковская частота. Вычисление множителя $S(\vec {k})$ требует знания конкретного вида потенциальных ям, образующих СР. Использован простой модельный случай (как и в [14]), когда $\varphi (x) = {\text{const}}$ при 0 ≤ x ≤ d, и $\varphi (x) = 0$ при x < 0, x > d (φ – волновая функция состояния, соответствующего рассматриваемой разрешенной минизоне, в одной из потенциальных ям, образующих СР)

(5)

$S\left( {{{k}_{x}},{{k}_{y}}} \right) = 4d\sum\limits_{n,m} {\frac{{(1 - \cos \left( {{{k}_{x}}d} \right))(1 - \cos \left( {{{k}_{y}}d} \right))}}{{{{{\left( {{{k}_{x}}d + 2\pi n} \right)}}^{2}}{{{\left( {{{k}_{y}}d + 2\pi m} \right)}}^{2}}\sqrt {{{{\left( {{{k}_{x}}d + 2\pi n} \right)}}^{2}} + {{{({{k}_{y}}d + 2\pi m)}}^{2}}} }}} .$

Предполагаем, как и в [14], что в состоянии равновесия носители заряда подчиняются статистике Больцмана $n(\vec {p}) = A\exp ({{ - \varepsilon (\vec {p})} \mathord{\left/ {\vphantom {{ - \varepsilon (\vec {p})} {{{k}_{b}}T}}} \right. \kern-0em} {{{k}_{b}}T}}),$ где T – температура, k_b – постоянная Больцмана, А – постоянная нормировки.

Для полупроводниковых СР с неаддитивным энергетическим спектром из (4) удается получить аналитическое выражение для поляризационного оператора (4) в случае высоких температур (Δ $ \ll $ k_bT). Это в дальнейшем значительно облегчает нахождение закона дисперсии плазменных волн. Таким образом, (4) преобразуется к виду

(6)

$\begin{gathered} - \frac{{2\pi {{e}^{2}}NS(\vec {k})}}{{\chi {{k}_{b}}T}}J_{0}^{2}\left( {\frac{\Delta }{{\hbar {{\Omega }_{{st}}}}}\sin ({{{{k}_{x}}d} \mathord{\left/ {\vphantom {{{{k}_{x}}d} 2}} \right. \kern-0em} 2})} \right) \times \\ \times \,\,\left[ {1 - \frac{w}{{\sqrt {{{w}^{2}} - 1} }} + {{{\left( {\frac{\delta }{{\hbar {{\Omega }_{{st}}}}}} \right)}}^{2}}\left\{ {\cos ({{k}_{y}}d) \times } \right.} \right. \\ \times \,\,(1 + 2\pi (1 - 2{{w}^{2}})) - 1 + \frac{w}{{\sqrt {{{w}^{2}} - 1} }} \times \\ \left. { \times \,\,(1 + \cos ({{k}_{y}}d)(4\pi ({{w}^{2}} - 1) - 1))\} } \right] = 1, \\ \end{gathered} $

где $w = {{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {\Delta \sin ({{{{k}_{y}}d} \mathord{\left/ {\vphantom {{{{k}_{y}}d} 2}} \right. \kern-0em} 2})}}} \right. \kern-0em} {\Delta \sin ({{{{k}_{y}}d} \mathord{\left/ {\vphantom {{{{k}_{y}}d} 2}} \right. \kern-0em} 2})}}.$ Как видно из (4), (6) поляризационный оператор имеет малую поправку для СР со слабой неаддитивностью, что и объясняет схожее поведение законов дисперсии плазменных волн $\omega (\vec {k})$ в сильном статическом электрическом поле для 2D-ГСР [15] и узкозонных полупроводниковых 2D-СР [5].

Для ГСР разложение по малому параметру (Δ/k_bT) неприменимо, по крайней мере для рассматриваемой в работе структуры, так как при этом нарушается условие одноминизонного приближения. Поэтому анализ закона дисперсии плазменных волн $\omega (\vec {k})$ в виду сложности (4) производился численно.

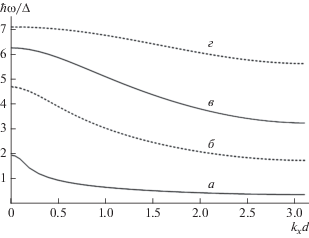
На рис. 2 приведены дисперсионные кривые ω(k_x) 2D-ГСР, находящейся в сильном электрическом поле для разных значений компоненты волнового вектора k_y. Влияние сильного статического электрического поля приводит к характерной зависимости ω(k_x): с увеличением компоненты волнового вектора k_x частота плазменных колебаний уменьшается, в то время как в отсутствие электрического поля увеличение k_x приводит к росту плазменной частоты. Похожая дисперсионная зависимость ω(k_x) наблюдалась и для плазменных волн в электронном 2D-газе полупроводниковых 2D-СР в присутствии сильного постоянного электрического поля [15] и для одномерных ГСР [5].

Рис. 2.

Закон дисперсии ω(k_x) при T = 70 К, $\Delta {\text{/}}2\hbar \Omega $ = = 0.1, концентрации N = 10¹¹ см^–2, a – k_yd = 0.1, б – k_yd = 0.5, в – k_yd = 1.0, г – k_yd = 3.1.

Сделаем численные оценки. При концентрации N₀ = 10¹¹ см^–2, d =2 ⋅ 10^–6 см, d₁ = d₂, Δ_SiC = 0.13 эВ, $\Delta {\text{/}}2\hbar \Omega $ = 0.1, T = 70 K, k_x = k_y ≈ 10⁶ см^–1 получаем, что частота плазменных колебаний составляет по порядку величины ω ≈ 10¹⁴ с^–1.

В отсутствие электрического поля для полупроводниковых СР со слабой неаддитивностью энергетического спектра (3) и широкой запрещенной зоной также удается аналитически получить выражение для поляризационного оператора $\Pi (\vec {k},\omega )$ в случае высоких температур (g₂Δ_SiC$ \ll $ k_bT). Подставляя $\Pi (\vec {k},\omega )$ в (4), получаем окончательное выражение для нахождения закона дисперсии плазменных волн $\omega (\vec {k})$

(7)

$\begin{gathered} \frac{{2\pi {{e}^{2}}NS(\vec {k})}}{{\chi {{k}_{b}}T}}\left[ {\frac{{\delta {{\Delta }^{2}}}}{{16{{{({{k}_{b}}T)}}^{3}}}} - 1} \right] \times \\ \times \,\,\left[ {1 - \frac{2}{\pi }\frac{{\hbar \omega K(z)}}{{\sqrt {{{{(\hbar \omega )}}^{2}} - {{\Delta }^{{\text{2}}}}{{{\left( {\sin \frac{{{{k}_{x}}d}}{2} - \sin \frac{{{{k}_{y}}d}}{2}} \right)}}^{2}}} }}} \right] = 1, \\ \end{gathered} $

где N – поверхностная плотность электронного 2D-газа, K(z) – полный эллиптический интеграл первого рода,

(8)

$z = 2\Delta \sqrt {{{\sin \frac{{{{k}_{x}}d}}{2}\sin \frac{{{{k}_{y}}d}}{2}} \mathord{\left/ {\vphantom {{\sin \frac{{{{k}_{x}}d}}{2}\sin \frac{{{{k}_{y}}d}}{2}} {\left( {{{{(\hbar \omega )}}^{2}} - {{\Delta }^{2}}{{{\left( {\sin \frac{{{{k}_{x}}d}}{2} - \sin \frac{{{{k}_{y}}d}}{2}} \right)}}^{2}}} \right)}}} \right. \kern-0em} {\left( {{{{(\hbar \omega )}}^{2}} - {{\Delta }^{2}}{{{\left( {\sin \frac{{{{k}_{x}}d}}{2} - \sin \frac{{{{k}_{y}}d}}{2}} \right)}}^{2}}} \right)}}} .$

Как видно из (7), отличие полученного уравнения от аналогичного для полупроводниковой СР с аддитивным спектром [14] состоит в появлении сомножителя с коэффициентом g₃, являющимся параметром, характеризующим неаддитивность спектра. Таким образом, слабая неаддитивность энергетического спектра приводит к перенормировке концентрации носителей, и плазменная частота в таких структурах меньше, чем в структурах с аддитивным спектром при одинаковых параметрах сравниваемых структур.

Данная задача решалась в пренебрежении столкновениями электронов с фононами, примесями и другими дефектами. Такое возможно, когда период плазменных колебаний мал по сравнению со временем свободного пробега электрона τ (ωτ $ \gg $ 1). Это условие может быть удовлетворено при τ ≥ ≥ 10^–12 c, что является легко выполнимым для графена и структур на его основе.

При сравнительном исследовании одночастичных и коллективных возбуждений в двумерном электронном газе 2D-ГСР установлено, что коллективные возбуждения перекрываются одночастичными в низкоэнергетической области. Это приведет к отличию теоретических вычислений от экспериментальных данных в начальной области энергий.

ЗАКЛЮЧЕНИЕ

Предложен подход, позволяющий оценить влияние неаддитивности энергетического спектра на физические законы в 2D-СР, и в частности, на закон дисперсии плазменных волн. Для СР со слабой неаддитивностью в спектре и широкой запрещенной зоной получены аналитически выражения для нахождения закона дисперсии плазменных волн, как в отсутствие внешних воздействий, так и в сильном электрическом поле. Показано, что полученные дисперсионные зависимости $\omega (\vec {k})$ для ГСР характерны для систем с искусственно созданным периодическим потенциалом.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-42-340005 и Минобрнауки России на выполнение государственных работ в сфере научной деятельности в рамках проектной части государственного задания (код проекта: 3.2797.2017/4.6).

Список литературы

Shur M.S. Introduction to electronic devices. New York: Wiley, 1995.
Муравьев В.М., Кукушкин И.В., Смет Ю. и др. // Письма в ЖЭТФ. 2009. Т. 90. № 3. С. 216; Muravev V.M., Kukushkin I.V., Smet J. et al. // JETP Lett. 2009. V. 90. № 3. P. 197.
Глазов С.Ю., Ковалев А.А., Мещерякова Н.Е. // Изв. РАН. Сер. физ. 2012. Т. 76. № 12. С. 1479; Glazov S.Yu., Kovalev A.A., Mescheryakova N.E. // Bull. Russ. Acad. Sci. Phys. 2012. V. 76. № 12. P. 1323.
Ратников П.В., Силин А.П. // Письма в ЖЭТФ. 2015. Т. 102. № 11. С. 823; Ratnikov P.V., Silin A.P. // JETP Lett. 2015. V. 102. № 11. P. 713.
Глазов С.Ю., Ковалев А.А., Мещерякова Н.Е. // ФТП. 2015. Т. 49. № 4. С. 515; Glazov S.Yu., Kovalev A.A., Meshcheryakova N.E. // Semicond. 2015. V. 49. № 4. P. 504.
Глазов С.Ю., Ковалев А.А. // Изв. РАН. Сер.физ. 2018. Т. 82. № 1. С. 105; Glazov S.Yu., Kovalev A.A. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. № 1. P. 94.
Kryuchkov S.V., Popov C.A. // J. Nano Electron. Phys. 2017. V. 9. № 2. P. 02013.
Forsythe C., Zhou X., Watanabe K. et al. // Nature Nanotech. 2018. V. 13. P. 566.
Zhang Y., Kim Y., Gilbert M. J. et al. // arXiv: 1703.05689. 2018.
Завьялов Д.В., Конченков В.И., Крючков С.В. // ФТП. 2012. Т. 46. № 1. С. 113; Zavialov D.V., Konchenkov V.I., Kruchkov S.V. // Semicond. 2012. V. 46. № 1. P. 109.
Ратников П.В. // Письма в ЖЭТФ. 2009. Т. 90. № 6. С. 515; Ratnikov P.V. // JETP Lett. 2009. V. 90. № 6. P. 469.
Крючков С.В., Сыродоев Г.А. // Изв. вузов. Радиофиз. 1990. № 6. С. 762.
Бадикова П.В., Глазов С.Ю., Сыродоев Г.А. // ФТП. 2019. Т. 53. № 7. С. 927; Badikova P.V., Glazov S.Yu., Syrodoev G.A. // Semicond. 2019. V. 53. № 7. P. 911.
Глазов С.Ю., Крючков С.В. // ФТП. 2000. Т. 34. № 7. С. 835; Glazov S.Yu., Kryuchkov S.V. // Semicond. 2000. V. 34. № 7. P. 807.
Глазов С.Ю., Крючков С.В. // ФТП. 2001. Т. 35. № 4. С. 456; Glazov S.Yu., Kryuchkov S.V. // Semicond. 2001. V. 35. № 4. P. 444.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал