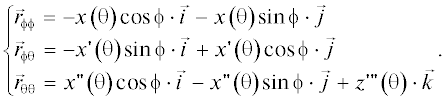Известия РАН. Серия физическая, 2020, T. 84, № 2, стр. 214-218

Взаимосвязь плотности распределения заряда с кривизной поверхности объемного проводника

П. А. Поляков^1, *, Н. Е. Русакова¹, Ю. В. Самухина¹

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

^* E-mail: polyakovpa@mail.ru

Поступила в редакцию 26.08.2019
После доработки 13.09.2019
Принята к публикации 28.10.2019

DOI: 10.31857/S0367676520020325

Полный текст (PDF)

Аннотация

Исследована кривизна поверхности твердого проводящего тела сложной формы. Проведено сравнение полученной зависимости с распределением зарядов по поверхности проводящего тела. Показано, что для такого тела максимальные значения кривизны и поверхностной плотности распределения зарядов достигаются в разных точках поверхности.

ВВЕДЕНИЕ

Рассмотрим соответствие между величиной плотности распределения заряда по поверхности твердого проводящего тела вращения сложной формы и кривизной поверхности. Известно, что в общем случае распределение заряда по поверхности проводника не является равномерным. Согласно некоторым классическим учебникам (см., например, [1, 2]) максимальное значение плотности распределения заряда по поверхности соответствует максимальной кривизне данной поверхности. Исследования по установлению зависимости поверхностной плотности заряда от кривизны поверхности проводятся до настоящего времени. В более ранних работах [3–6] значение плотности заряда в любой точке проводящей поверхности считается пропорциональным корню четвертой степени из гауссовой кривизны в данной точке. Однако в более поздней публикации [7] доказано, что это не совсем так. В настоящей работе установлена частичная зависимость между поверхностной плотностью электрического заряда и корнем четвертой степени из гауссовой кривизны. Поверхностная плотность электрического заряда зависит и от других функций, поверхностных координат. На основе аналитических расчетов можно показать, что в точках, где плотность заряда максимальна, кривизна поверхности не достигает максимальных значений.

ФОРМА ИССЛЕДУЕМОЙ ПРОВОДЯЩЕЙ ПОВЕРХНОСТИ И ПОВЕРХНОСТНАЯ ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ЗАРЯДА ПО ДАННОЙ ПОВЕРХНОСТИ

Ранее была разработана методика расчета аналитических выражений для плотности распределения заряда и формы поверхности нового класса тел вращения, для которых возможно точное решение задачи электростатики. Эта методика представлена в работах [8–11]. Для рассматриваемых тел потенциал на поверхности тела зависит только от полярного угла и не зависит от азимутального, то есть поверхности данных тел являются поверхностями вращения относительно оси Z.

Рассмотрим одно из проводящих тел вращения, принадлежащих этому классу. Пусть постоянный потенциал ${{\varphi }_{\Sigma }}$ на поверхности этого тела задается формулой [8–11]:

(1)

$\frac{1}{{4\pi {{\varepsilon }_{0}}}}\left( {\frac{{{{a}_{0}}}}{r} \pm \frac{{{{a}_{1}}}}{{{{r}^{2}}}}{{P}_{1}}(\cos \theta )} \right) = {{\varphi }_{\Sigma }},\,\,\,\,\phi \in [0;2\pi ),$

где ${{\varepsilon }_{0}}$ – электрическая постоянная, ${{a}_{1}}$ и ${{a}_{0}}$ – некоторые постоянные, ${{P}_{1}}(\cos \theta )$ – полином Лежандра первой степени. Параметр ${{a}_{0}}$ имеет смысл суммарного электрического заряда $q,$ распределенного по поверхности, задаваемой уравнением (1).

Введем безразмерные параметры:

(2)

$\xi = {r \mathord{\left/ {\vphantom {r {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}},\,\,\,\,\Psi = \frac{{{{\varphi }_{\Sigma }}}}{{{{\varphi }_{0}}}} = \frac{{{{\varphi }_{\Sigma }}}}{{{{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {4\pi {{\varepsilon }_{0}}{{r}_{0}}}}} \right. \kern-0em} {4\pi {{\varepsilon }_{0}}{{r}_{0}}}}}},$

где ${{r}_{0}}$ и $q = {{a}_{0}}$ – радиус и заряд заряженной проводящей сферы, ξ – безразмерный радиус-вектор, нормированный на радиус этой сферы, и Ψ – безразмерный потенциал, нормированный на потенциал сферы ${{\varphi }_{0}} = {{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {\left( {4\pi {{\varepsilon }_{0}}{{r}_{0}}} \right)}}} \right. \kern-0em} {\left( {4\pi {{\varepsilon }_{0}}{{r}_{0}}} \right)}}.$

В терминах безразмерных параметров (2) выражение для потенциала принимает следующий вид

(3)

$\Psi {{\xi }^{2}} - \xi \mp {{k}_{1}}\cos \theta = 0,$

где ${{k}_{1}} = {{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} {\left( {{{a}_{0}}{{r}_{0}}} \right)}}} \right. \kern-0em} {\left( {{{a}_{0}}{{r}_{0}}} \right)}}$ – безразмерный коэффициент.

При выборе в (3) знаков “+” и “–” имеем две идентичные фигуры, зеркально симметричные относительно друг друга. Решение уравнения (3) со знаком “–” позволяет получить уравнение поверхности рассматриваемого тела в безразмерных сферических координатах $\left( {\xi ,\theta ,\phi } \right)$ в следующем виде [8, 9, 11]:

(4)

$\xi \left( \theta \right) = \frac{{1 + \sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } }}{{2\Psi }},\,\,\,\,\phi \in [0;2\pi ),$

где Ψk₁ должно удовлетворять условию:

(5)

$\Psi {{k}_{1}} \leqslant {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}.$

Если значение произведения $\Psi {{k}_{1}}$ не удовлетворяет этому условию, величина $\xi \left( \theta \right)$ будет комплексной, и полученная поверхность будет иметь разрывы.

Тогда поверхностная плотность распределения заряда, в соответствии с уравнением может быть записана в следующем безразмерном виде [8, 9, 11]:

(6)

$\tilde {\sigma } = \frac{\sigma }{{{{\sigma }_{0}}}} = \sqrt {\frac{{64{{\Psi }^{6}}k_{1}^{2}{{{\sin }}^{2}}\theta }}{{{{{\left( {1 + \sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } } \right)}}^{6}}}} + {{{\left( {\frac{{16{{\Psi }^{3}}{{k}_{1}}\cos \theta + 4{{\Psi }^{2}}\left( {1 + \sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } } \right)}}{{{{{\left( {1 + \sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } } \right)}}^{3}}}}} \right)}}^{2}}} ,$

где $\sigma $ – плотность распределения зарядов по поверхности проводника, ${{\sigma }_{0}} = {{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {\left( {4\pi r_{0}^{2}} \right)}}} \right. \kern-0em} {\left( {4\pi r_{0}^{2}} \right)}}$ – поверхностная плотность зарядов для заряженной сферы, используемой в нормировке (2).

Для графического представления формы поверхности и распределения заряда зададим систему координат:

(7)

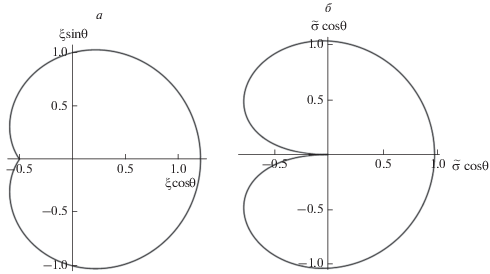
$\left\{ \begin{gathered} X = \xi \sin \theta \sin \phi \hfill \\ Y = \xi \sin \theta \cos \phi \hfill \\ Z = \xi \cos \theta \hfill \\ \end{gathered} \right..$

На рис. 1а и 1б приведены, соответственно, форма поверхности (4) и распределение заряда (6) по поверхности рассматриваемого проводящего тела при значениях параметров $\Psi = 1$ и ${{k}_{1}} = 0.25$ в сечении плоскостью, проходящей через ось Oz перпендикулярно плоскости Oxy.

Рис. 1.

а – Сечение поверхности вращения, задаваемой формулой (3), плоскостью, проходящей через ось Oz перпендикулярно координатной плоскости Oxy; б – распределение заряда (6) по поверхности фигуры вращения, задаваемой (3).

КРИВИЗНА ПОВЕРХНОСТИ ПРОВОДЯЩЕГО ТЕЛА

Рассчитаем зависимость кривизны для нашего тела вращения. Уравнение поверхности определяется формулой (3), а поверхностная плотность распределения заряда имеет вид (6).

Введем обозначения:

(8)

$x(\theta ) = \xi \left( \theta \right)\sin \theta ;\,\,\,\,z(\theta ) = \xi \left( \theta \right)\cos \theta ,$

где ξ(θ) определяется формулой (3). Вычислим коэффициенты первой квадратичной формы нашей поверхности вращения [12]. Для этого сначала рассчитаем первые производные $x{\kern 1pt} '(\theta )$ и $z{\kern 1pt} '(\theta ){\text{:}}$

(9)

$\left\{ {\begin{array}{*{20}{c}} {x{\kern 1pt} '(\theta ) = \frac{{\cos \theta (1 + \sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } )}}{{2\Psi }} - \frac{{{{k}_{1}}{{{\sin }}^{2}}\theta }}{{\sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } }}} \\ {z{\kern 1pt} '(\theta ) = - \frac{{{{k}_{1}}\cos \theta \sin \theta }}{{\sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } }} - \frac{{(1 + \sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } )\sin \theta }}{{2\Psi }}} \end{array}} \right..$

Запишем уравнение, определяющее нашу поверхность вращения в виде [13]:

(10)

$\vec {r}\left( {\varphi ,\theta } \right) = x\left( \theta \right)\cos \phi \cdot \vec {i} + x\left( \theta \right)\sin \phi \cdot \vec {j} + z\left( \theta \right) \cdot \vec {k},$

где $\vec {i},\vec {j},\vec {k}$ – единичные векторы вдоль осей x, y, z соответственно.

(11)

$\left\{ \begin{gathered} {{{\vec {r}}}_{\phi }} = - x\left( \theta \right)\sin \phi \cdot \vec {i} + x\left( \theta \right)\cos \phi \cdot \vec {j} \hfill \\ {{{\vec {r}}}_{{\theta }}} = x{\kern 1pt} '\left( \theta \right)\cos \phi \cdot \vec {i} + x{\kern 1pt} '\left( \theta \right)\sin \phi \cdot \vec {j} + z{\kern 1pt} '\left( \theta \right) \cdot \vec {k} \hfill \\ \end{gathered} \right..$

Обозначим коэффициенты первой квадратичной формы поверхности E, F, G и получим выражения для этих коэффициентов:

(12)

$\begin{gathered} E = \vec {r}_{\phi }^{2} = x{\kern 1pt} '\left( \theta \right);\,\,\,\,F = \left( {{{{\vec {r}}}_{\phi }},{{{\vec {r}}}_{{\theta }}}} \right) = 0; \\ G = \vec {r}_{{\theta }}^{2} = {{\left( {x{\kern 1pt} '\left( \theta \right)} \right)}^{2}} + {{\left( {z{\kern 1pt} '\left( \theta \right)} \right)}^{2}}. \\ \end{gathered} $

В терминах наших безразмерных параметров получим:

(13)

$\left\{ \begin{gathered} E = \frac{{{{{\left( {1 + \sqrt {1 + 4\Psi {{k}_{1}}\cos \theta } } \right)}}^{2}}{{{\sin }}^{2}}\theta }}{{4{{\Psi }^{2}}}} \hfill \\ F = 0 \hfill \\ G = \frac{{1 + {{\Psi }^{2}}k_{1}^{2}\left( {5 + 3\cos 2\theta } \right) + 6\Psi {{k}_{1}}\cos \theta + {{{\left( {1 + 4\Psi {{k}_{1}}\cos \theta } \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{2{{\Psi }^{2}}\left( {1 + 4\Psi {{k}_{1}}\cos \theta } \right)}} \hfill \\ \end{gathered} \right..$

Для нахождения коэффициентов второй квадратичной формы произведем следующие вычисления:

(14)

$\left[ {{{{\vec {r}}}_{\phi }},{{{\vec {r}}}_{{\theta }}}} \right] = x\left( \theta \right)z{\kern 1pt} '\left( \theta \right)\cos \phi \cdot \vec {i} + \,\,x\left( \theta \right)z{\kern 1pt} '\left( \theta \right)\sin \phi \cdot \vec {j} - x\left( \theta \right)x{\kern 1pt} '\left( \theta \right) \cdot \vec {k}.$

Единичный вектор нормали к поверхности определяется формулой [12]

(15)

$\vec {n} = \frac{{\left[ {{{{\vec {r}}}_{\phi }},{{{\vec {r}}}_{\theta }}} \right]}}{{\left| {\left[ {{{{\vec {r}}}_{\phi }},{{{\vec {r}}}_{\theta }}} \right]} \right|}} = \frac{{z{\kern 1pt} '\left( \theta \right)\cos \phi \cdot \vec {i} + z{\kern 1pt} '\left( \theta \right)\sin \phi \cdot \vec {j} - x{\kern 1pt} '\left( \theta \right) \cdot \vec {k}}}{{\sqrt {{{{\left( {x{\kern 1pt} '\left( \theta \right)} \right)}}^{2}} + {{{\left( {z{\kern 1pt} '\left( \theta \right)} \right)}}^{2}}} }},$

(16)

Следовательно, коэффициенты второй квадратичной формы поверхности определяются следующими выражениями:

(17)

С учетом формулы (13) коэффициенты второй квадратичной квадратичной формы в безразмерных координатах имеют вид:

(18)

$\left\{ \begin{gathered} L = \frac{{\left( {1 + \sqrt {1 + 4A} } \right)\left( {1 + 6A + \sqrt {1 + 4A} } \right){{{\sin }}^{2}}\theta }}{{2\sqrt 2 {{\Psi }^{2}}\sqrt {1 + 4A} \sqrt {\frac{{1 + 5{{\Psi }^{2}}k_{1}^{2} + 6A + \sqrt {1 + 4A} + 4A\sqrt {1 + 4A} + 3{{\Psi }^{2}}k_{1}^{2}\cos 2\theta }}{{{{\Psi }^{2}}\left( {1 + 4A} \right)}}} }} \hfill \\ N = \frac{{1 + 11{{\Psi }^{2}}k_{1}^{2} + 9A + 9{{\Psi }^{2}}k_{1}^{2}\cos 2\theta + \sqrt {1 + 4A} \left( {1 + 9{{\Psi }^{2}}k_{1}^{2} + 7A + 3{{\Psi }^{2}}k_{1}^{2}\cos 2\theta } \right)}}{{\sqrt 2 {{\Psi }^{2}}{{{\left( {1 + 4A} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\sqrt {\frac{{1 + 5{{\Psi }^{2}}k_{1}^{2} + 6A + \sqrt {1 + 4A} + 4A\sqrt {1 + 4A} + 3{{\Psi }^{2}}k_{1}^{2}\cos \theta }}{{{{\Psi }^{2}}\left( {1 + 4A} \right)}}} }} \hfill \\ \end{gathered} \right.,$

где $A = \Psi {{k}_{1}}\cos \theta .$ Обозначим через k₁ и k₂ главные кривизны поверхности вращения. Главные кривизны выражаются через коэффициенты первой и второй квадратичной формы [14]:

(19)

${{K}_{1}} = \frac{L}{E},\,\,\,\,{{K}_{2}} = \frac{N}{G},$

а в безразмерном виде:

$\left\{ \begin{gathered} {{K}_{1}} = \frac{{2\left( {1 + 6A + \sqrt {1 + 4A} } \right)}}{{\sqrt {1 + 4A} \left( {1 + \sqrt {1 + 4A} } \right)\sqrt {\frac{{1 + 5{{\Psi }^{2}}k_{1}^{2} + 6A + \sqrt {1 + 4A} + 4A\sqrt {1 + 4A} + 3{{\Psi }^{2}}k_{1}^{2}\cos 2\theta }}{{{{\Psi }^{2}}\left( {1 + 4A} \right)}}} }} \hfill \\ {{K}_{2}} = \frac{{\sqrt 2 \left( {1 + 11{{\Psi }^{2}}k_{1}^{2} + 9A + 9{{\Psi }^{2}}k_{1}^{2}\cos 2\theta + \sqrt {1 + 4A} \left( {1 + 9{{\Psi }^{2}}k_{1}^{2} + 7A + 3{{\Psi }^{2}}k_{1}^{2}\cos 2\theta } \right)} \right)}}{{{{{\left( {1 + 4A} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\sqrt {\frac{{{{{\left( {1 + 5{{\Psi }^{2}}k_{1}^{2} + 6A + \sqrt {1 + 4A} + 4A\sqrt {1 + 4A} + 3{{\Psi }^{2}}k_{1}^{2}\cos 2\theta } \right)}}^{3}}}}{{{{\Psi }^{2}}}}} }} \hfill \\ \end{gathered} \right..$

Согласно [14] средняя кривизна определяется формулой:

(20)

$H = \frac{1}{2}\left( {{{K}_{1}} + {{K}_{2}}} \right).$

На рис. 2 приведен график зависимости средней кривизны $H\left( \theta \right)$ и безразмерной плотности поверхностного распределения зарядов $\tilde {\sigma }\left( \theta \right)$ от полярного угла $\theta \in \left[ {0,\pi } \right]$ при значениях параметров $\Psi = 1$ и $k = 0.22.$

Рис. 2.

Зависимость средней кривизны $H\left( \theta \right)$ (сплошная кривая) и безразмерной плотности распределения заряда $\tilde {\sigma }\left( \theta \right)$ по поверхности (пунктирная кривая) от полярного угла θ.

На рис. 3а и 3б построены графики зависимостей производных от плотности распределения зарядов по поверхности проводника $\tilde {\sigma }{\kern 1pt} '\left( \theta \right)$ и от средней кривизны $H{\kern 1pt} '\left( \theta \right)$ при значениях параметров $\Psi = 1$ и $k = 0.22.$ Нули этих зависимостей соответствуют экстремумам средней кривизны $H\left( \theta \right)$ и безразмерной плотности поверхностного распределения зарядов $\tilde {\sigma }\left( \theta \right).$

Рис. 3.

а – Зависимость производной плотности распределения заряда по поверхности $\tilde {\sigma }{\kern 1pt} '$ от угла θ; б – зависимость производной средней кривизны $H{\kern 1pt} '$ от угла θ.

Расчеты показывают, что производные функций поверхностного распределения заряда $\tilde {\sigma }{\kern 1pt} '\left( \theta \right)$ и средней кривизны поверхности $H\left( \theta \right)$ обращаются в ноль при значениях θ = 1.82 и θ = 1.99 соответственно. Поскольку производные функций при переходе через соответствующие точки меняют свой знак с плюса на минус, максимальное значение плотности распределения заряда по поверхности вращения достигается при θ = 1.82, а средняя кривизна имеет максимальное значение при θ = 1.99. Таким образом, максимумы отличаются примерно на 10 градусов (0.17 радиан) по углу $\theta $.

ЗАКЛЮЧЕНИЕ

Таким образом доказано, что для класса тел, описанного в работах [8–11] точки поверхности проводящего тела, в которых достигаются максимальные значения средней кривизны и плотности поверхностного распределения заряда не совпадают. Следовательно, для такого тела нельзя однозначно сказать, что большее значения поверхностной плотности заряда соответствует большему значению кривизны.

Список литературы

Landau L.D. Electrodynamics of continuous media. Course of theoretical physics. V. 8. Oxford: Pergamon Press, 1984. 460 p.
Smythe W.B. Static and dynamic electricity. N.Y.: McGgraw-Hill Book Company Inc., 1988. 400 p.
Enze L. // J. Phys. D. 1986. V. 19. № 1. P. 1.
Enze L. // J. Phys. D. 1987. V. 20. № 12. P. 160.
Liu K.M. // Amer. J. Phys. 1987. V. 55. № 9. P. 849.
McAllister I.W. // J. Phys. D. 1990. V. 23. № 3. P. 359.
Bhattacharya K. // Phys. Scr. 2016. V. 91. № 3. P. 355.
Поляков П.А., Русакова Н.Е., Самухина Ю.В. // Вестн. Моск. ун-та. Сер. 3. Физ. Астрон. 2014. № 6. С. 57.
Polyakov P.A., Rusakova N.E., Samukhina Y.V. // J. Electrostat. 2015. V. 77. P. 147.
Поляков П.А., Русакова Н.Е., Самухина Ю.В., Стока Г.П. // Сб. тр. XXIV Межд. конф. “Электромагнитное поле и материалы (Фундаментальные физические исследования)". (Москва, 2016). С. 248.
Самухина Ю.В. Теоретическое исследование статического и динамического самосогласованного электромагнитного поля. Дисс. … канд. физ.-мат. наук. Москва: МГУ им. М.В. Ломоносова. 2016
Ильин В.A., Позняк Э.Г. Основы математического анализа. Часть 2. М.: Физматлит, 2004. 464 с.
Погорелов А.В. Дифференциальная геометрия. М.: Наука, 1974. 176 с.
Смирнов В.И. Курс высшей математики. Т. 2. М.: Наука, 1974. 656 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал