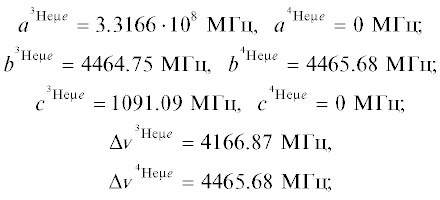Известия РАН. Серия физическая, 2020, T. 84, № 3, стр. 336-340

Тонкая и сверхтонкая структура мюонного гелия

А. В. Эскин^1, *, В. И. Коробов^1, 2, А. П. Мартыненко¹, В. В. Сорокин¹

¹ Федеральное государственное автономное образовательное учреждение высшего образования “Самарский национальный исследовательский университет имени академика С.П. Королева”
Самара, Россия

² Международная межправительственная организация Объединенный институт ядерных исследований
Дубна, Россия

^* E-mail: EskinAlexey1992@gmail.com

Поступила в редакцию 20.09.2019
После доработки 15.11.2019
Принята к публикации 27.11.2019

DOI: 10.31857/S0367676520030096

Полный текст (PDF)

Аннотация

Вычислена тонкая и сверхтонкая структура уровней энергии мюонного гелия на основе стохастического вариационного метода. Базисные волновые функции взяты в гауссовой форме. Матричные элементы гамильтониана вычислены аналитически. Для численного расчета написан компьютерный код в системе MATLAB. В результате получены численные значения энергий связанного состояния, сверхтонкой структуры спектра, поправок на структуру ядра, релятивизм и поляризацию вакуума.

ВВЕДЕНИЕ

Квантовая электродинамика (КЭД) связанных состояний была проверена с помощью прецизионных измерений в широком классе задач. Экспериментальная программа коллаборации CREMA (Charge Radius Experiments with Muonic Atoms) по исследованию тонкой и сверхтонкой структуры спектров энергии простейших мюонных атомов успешно выполняется, начиная с 2010 г., когда были измерены частоты двух переходов в мюонном водороде [1, 2]. В мюонном дейтерии методами лазерной спектроскопии были измерены 3 частоты переходов между уровнями 2P и 2S [3, 4]. Эти измерения позволили получить на порядок более точные значения зарядовых радиусов протона и дейтрона и выявить значительное отличие этих значений от величин, которые получаются из экспериментов с электронными атомами.

Еще одна важная и интересная проблема в физике мюоных систем связана с мюонными молекулярными ионами водорода (tdμ, tpμ, dpμ и др.), после образования которых происходит слияние их ядер за счет сильного взаимодействия (реакции мюонного катализа [5]). Для теоретического описания протекающих при этом физических процессов, связанных с мезоатомными, мезомолекулярными и ядерными явлениями, необходимо знать структуру уровней энергии мезоатомов и мезомолекул. В случае мезоатомов (μt, μd, μp) расчет тонкой и сверхтонкой структуры (СТС) спектра выполнен в последние годы с высокой точностью [6–8]. Использование вариационного метода для трехчастичных систем (мезомолекул) позволило достичь очень высокой точности решения уравнения Шредингера [9, 10] с базовыми членами гамильтониана системы. Однако прецизионное исследование уровней энергии требует учета различных поправок в гамильтониане взаимодействия в рамках квантовой электродинамики. В данной работе мы исследуем уровни энергии мюонного гелия в рамках стохастического вариационного метода [11–14]. Цель работы состоит в расчете уровней энергии основного состояния, а также сверхтонкой структуры спектра с учетом релятивистских поправок, поправок на структуру ядра и эффектов поляризации вакуума.

ОБЩИЙ ФОРМАЛИЗМ

В рамках вариационного метода пробная функция для системы трех частиц может быть записана в следующем расширенном виде:

(1)

${\Psi } = \sum\limits_{i = 1}^K {{{c}_{i}}{\varphi }\left( {\vec {x},{{A}_{i}}} \right)} ,$

где ${\varphi }\left( {\vec {x},{{A}_{i}}} \right)$ – базисная функция, ${{c}_{i}}$ – линейные вариационные параметры, $\vec {x}$ – координаты Якоби, ${{A}_{i}}$ – нелинейные вариационные параметры, K – размер базиса. Верхняя граница для энергии основного состояния системы задается наименьшим собственным значением обобщенной задачи на собственные значения:

(2)

$HC = {{E}_{K}}BC,$

где ${{H}_{{ij}}} = \left\langle {\varphi \left( {{{x}_{i}},{{A}_{i}}} \right)\left| H \right|\varphi \left( {{{x}_{j}},{{A}_{j}}} \right)} \right\rangle ~$ – матричные элементы гамильтониана, A –матрица скалярных произведений базисных функций B_ij = = $~\left\langle {{\varphi }\left( {{{x}_{i}},{{A}_{i}}} \right)} \right|\left. {{\varphi }\left( {{{x}_{j}},{{A}_{j}}} \right)} \right\rangle ,$ С – вектор коэффициентов разложения волновой функции по базисным состояниям, ${{E}_{K}}$ – энергия связанного состояния трех частиц. Диагональные элементы 2 × 2-мерной симметричной, положительно определенной матрицы A соответствуют нелинейным параметрам гауссова разложения, а недиагональные элементы связывают различные относительные координаты, представляющие корреляции между частицами.

В атомной физике часто используется пробная функция ${\varphi }\left( {\vec {x},{{A}_{i}}} \right)~$ хиллерасовского типа или коррелированного экспоненциального типа. Эта функция содержит экспоненциальную форму, выраженную в терминах межчастичных координат. Вместо экспоненциальной функции мы используем ее гауссовский аналог [12]. В случае трех нетождественных частиц волновая функция для основного состояния имеет вид:

(3)

${{{\varphi }}_{{00}}}\left( {\vec {\rho },\vec {\lambda },A} \right) = {{e}^{{ - \frac{1}{2}\left[ {{{A}_{{11}}}{{{{\vec {\rho }}}}^{2}} + {{A}_{{22}}}{{{{\vec {\lambda }}}}^{2}} + 2{{A}_{{12}}}\left( {{\vec {\rho }} \cdot {\vec {\lambda }}} \right)} \right]}}}.$

Межчастичные расстояния выражаются через координаты Якоби ${\vec {\rho }}$ и ${\vec {\lambda }}$ следующим образом:

(4)

$\begin{gathered} {{{\vec {r}}}_{{12}}} = {{{\vec {r}}}_{1}} - {{{\vec {r}}}_{2}} = {\vec {\rho }},\,\,{{{\vec {r}}}_{{13}}} = {{{\vec {r}}}_{1}} - {{{\vec {r}}}_{3}} = {\vec {\lambda }} + \frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}{\vec {\rho }}, \\ {{{\vec {r}}}_{{23}}} = {{{\vec {r}}}_{2}} - {{{\vec {r}}}_{3}} = {\vec {\lambda }} - \frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}{\vec {\rho }}, \\ \end{gathered} $

где m₁, m₂ и m₃ – массы ядра гелия, электрона и мюона, ${{\vec {r}}_{{12}}}$ – радиус-вектор между ядром гелия и электроном, ${{\vec {r}}_{{13}}}$ – радиус-вектор между ядром гелия и мюоном, ${{\vec {r}}_{{23}}}$ – радиус-вектор между электроном и мюоном.

Матричные элементы для условия нормировки имеют следующий вид:

(5)

$\left\langle {{{\varphi }{\kern 1pt} {\text{'}}}} \mathrel{\left | {\vphantom {{{\varphi }{\kern 1pt} {\text{'}}} {\varphi }}} \right. \kern-0em} {{\varphi }} \right\rangle = \iint {d{\vec {\rho }}d{\vec {\lambda }}{{e}^{{ - \frac{1}{2}\left[ {{{B}_{{11}}}{{{{\vec {\rho }}}}^{2}} + {{B}_{{22}}}{{{{\vec {\lambda }}}}^{2}} + 2{{B}_{{12}}}\left( {{\vec {\rho }} \cdot {\vec {\lambda }}} \right)} \right]}}}} = \frac{{8{{{\pi }}^{3}}}}{{{{{(\det B)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}},$

где матрица коэффициентов $B = A + A{\kern 1pt} '.$ Аналогичным образом рассчитываются матричные элементы для кинетической энергии.

(6)

$\left\langle {\varphi {\kern 1pt} '} \right|\hat {T}\left| \varphi \right\rangle = - \frac{{24{{\pi }^{3}}}}{{{{{(\det B)}}^{{5{\text{/}}2}}}}}\left[ {\frac{{{{}^{2}}}}{{2{{\mu }_{1}}}}{{I}_{{\rho }}} + \frac{{{{}^{2}}}}{{2{{\mu }_{2}}}}{{I}_{{\lambda }}}} \right],$

(7)

$\begin{gathered} {{I}_{{\rho }}} = A_{{12}}^{2}{{B}_{{11}}} - 2{{A}_{{11}}}{{A}_{{12}}}{{B}_{{12}}} + \\ + \,\,{{A}_{{11}}}\left( {B_{{12}}^{2} + \left( {{{A}_{{11}}} - {{B}_{{11}}}} \right){{B}_{{22}}}} \right), \\ \end{gathered} $

(8)

$\begin{gathered} {{I}_{{\lambda }}} = A_{{12}}^{2}{{B}_{{22}}} - 2{{A}_{{22}}}{{A}_{{12}}}{{B}_{{12}}} + \\ + \,\,{{A}_{{22}}}\left( {B_{{12}}^{2} + \left( {{{A}_{{22}}} - {{B}_{{22}}}} \right){{B}_{{11}}}} \right), \\ \end{gathered} $

где приведенная масса представлена в виде: ${{\mu }_{1}} = \frac{{{{m}_{1}}{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}},$ ${{\mu }_{2}} = \frac{{\left( {{{m}_{1}} + {{m}_{2}}} \right){{m}_{3}}}}{{{{m}_{1}} + {{m}_{2}} + {{m}_{3}}}}.$

Матричные элементы оператора потенциальной энергии были вычислены аналитически:

(9)

$\left\langle {\varphi {\kern 1pt} '} \right|\hat {V}\left| \varphi \right\rangle = {{e}_{1}}{{e}_{2}}{{I}_{{12}}} + {{e}_{1}}{{e}_{3}}{{I}_{{13}}} + {{e}_{2}}{{e}_{3}}{{I}_{{23}}},$

(10)

$\begin{gathered} {{I}_{{12}}} = \frac{{8\sqrt 2 {{\pi }^{{5{\text{/}}2}}}}}{{\sqrt {{{B}_{{22}}}} \det B}}~,\,\,\,{{I}_{{13}}} = \frac{{8\sqrt 2 {{\pi }^{{5{\text{/}}2}}}}}{{\sqrt {F_{1}^{{13}}} \left( {{{B}_{{22}}}F_{1}^{{13}} - {{{\left( {F_{1}^{{13}}} \right)}}^{2}}} \right)}}, \\ {{I}_{{23}}} = \frac{{8\sqrt 2 {{\pi }^{{5{\text{/}}2}}}}}{{\sqrt {F_{1}^{{23}}} \left( {{{B}_{{22}}}F_{1}^{{23}} - {{{\left( {F_{1}^{{23}}} \right)}}^{2}}} \right)}}~, \\ F_{1}^{{13}} = {{B}_{{11}}} + {{B}_{{22}}}{{\left( {\frac{{{{m}_{2}}}}{{{{m}_{{12}}}}}} \right)}^{2}} - 2{{B}_{{12}}}\frac{{{{m}_{2}}}}{{{{m}_{{12}}}}}~, \\ F_{1}^{{23}} = {{B}_{{11}}} + {{B}_{{22}}}{{\left( {\frac{{{{m}_{1}}}}{{{{m}_{{12}}}}}} \right)}^{2}} + 2{{B}_{{12}}}\frac{{{{m}_{1}}}}{{{{m}_{{12}}}}}, \\ F_{2}^{{23}} = {{B}_{{12}}} - {{B}_{{22}}}\frac{{{{m}_{2}}}}{{{{m}_{{12}}}}},\,\,\,\,F_{2}^{{13}} = {{B}_{{12}}} + {{B}_{{22}}}\frac{{{{m}_{1}}}}{{{{m}_{{12}}}}}~, \\ ~{{m}_{{12}}} = {{m}_{1}} + {{m}_{2}}, \\ \end{gathered} $

где e₁, e₂, e₃ – заряды ядра гелия, электрона и мюона.

СВЕРХТОНКАЯ СТРУКТУРА ОСНОВНОГО СОСТОЯНИЯ

Для расчета сверхтонкой структуры необходимо вычислить матричные элементы сверхтонкой части гамильтониана взаимодействия. Потенциал сверхтонкого взаимодействия для основного состояния трехчастичной системы может быть получен из хорошо известного гамильтониана Брейта и записан в следующей удобной форме для трех взаимодействующих частиц со спинами S₁, S₂, S₃ соответственно:

(11)

$\begin{gathered} \Delta {{V}^{{hfs}}} = a\left( {{{{\vec {S}}}_{1}}{{{\vec {S}}}_{2}}} \right) + b\left( {{{{\vec {S}}}_{2}}{{{\vec {S}}}_{3}}} \right) + c\left( {{{{\vec {S}}}_{1}}{{{\vec {S}}}_{3}}} \right), \\ a = \frac{{2\pi {{\alpha }^{2}}}}{{3{{m}_{p}}{{m}_{2}}}}\frac{{{{\mu }_{N}}}}{{{{S}_{1}}}}\frac{{1 + {{\kappa }_{2}}}}{{{{S}_{2}}}}\left\langle {\delta \left( {{{{\vec {r}}}_{{12}}}} \right)} \right\rangle , \\ \end{gathered} $

(12)

$\begin{gathered} b = - \frac{{2\pi {{\alpha }^{2}}}}{{3{{m}_{2}}{{m}_{3}}}}\frac{{1 + {{\kappa }_{2}}}}{{{{S}_{2}}}}\frac{{1 + {{\kappa }_{3}}}}{{{{S}_{3}}}}\left\langle {\delta \left( {{{{\vec {r}}}_{{23}}}} \right)} \right\rangle , \\ c = \frac{{2\pi {{\alpha }^{2}}}}{{3{{m}_{p}}{{m}_{3}}}}\frac{{{{\mu }_{N}}}}{{{{S}_{1}}}}\frac{{1 + {{\kappa }_{3}}}}{{{{S}_{3}}}}\left\langle {\delta \left( {{{{\vec {r}}}_{{13}}}} \right)} \right\rangle . \\ \end{gathered} $

Матричные элементы дельта-функций имеют вид:

(13)

$\begin{gathered} \left\langle {\delta \left( {{{{\vec {r}}}_{{12}}}} \right)} \right\rangle ~ = \iint {d\vec {\rho }d\vec {\lambda }\delta \left( {\vec {\rho }} \right){{e}^{{ - \frac{1}{2}\left[ {{{B}_{{11}}}{{{{\vec {\rho }}}}^{2}} + {{B}_{{22}}}{{{{\vec {\lambda }}}}^{2}} + 2{{B}_{{12}}}\left( {{\vec {\rho }} \cdot {\vec {\lambda }}} \right)} \right]}}}} = \\ = \frac{{{{{\left( {2\pi } \right)}}^{{3{\text{/}}2}}}}}{{{{{\left( {{{B}_{{22}}}} \right)}}^{{3{\text{/}}2}}}}}, \\ \end{gathered} $

(14)

$\left\langle {\delta \left( {{{{\vec {r}}}_{{13}}}} \right)} \right\rangle ~ = \frac{{{{{\left( {2\pi } \right)}}^{{3{\text{/}}2}}}}}{{{{{\left( {{{B}_{{11}}} - 2{{B}_{{12}}}\frac{{{{m}_{2}}}}{{{{m}_{{12}}}}} + {{B}_{{22~}}}{{{\left( {\frac{{{{m}_{2}}}}{{{{m}_{{12}}}}}} \right)}}^{2}}} \right)}}^{{3{\text{/}}2}}}}}~,$

(15)

$\left\langle {\delta \left( {{{{\vec {r}}}_{{23}}}} \right)} \right\rangle ~ = \frac{{{{{\left( {2\pi } \right)}}^{{3{\text{/}}2}}}}}{{{{{\left( {{{B}_{{11}}} + 2{{B}_{{12}}}\frac{{{{m}_{1}}}}{{{{m}_{{12}}}}} + {{B}_{{22~}}}{{{\left( {\frac{{{{m}_{1}}}}{{{{m}_{{12}}}}}} \right)}}^{2}}} \right)}}^{{3{\text{/}}2}}}}}.$

где κ₂, κ₃ – аномальные магнитные моменты мюона и электрона, μ_N – магнитный момент ядра, m_p – масса протона. При расчете каждого вклада матричного элемента его необходимо разделить на коэффициент нормировки.

Отдельно необходимо рассмотреть поправку на структуру ядра, релятивистскую поправку и поправку на поляризацию вакуума к энергии основного состояния. Поправка на поляризацию вакуума в электронных атомных единицах имеет вид:

(16)

где фактор γ = 1/α, ζ – спектральный параметр. При расчете спектра энергии мы учитываем также поправку на структуру ядра для основного состояния мюонного гелия. Данная поправка может быть получена при помощи разложения электрического формфактора ядра:

(17)

${{\left. {{{G}_{E}}\left( {{{k}^{2}}} \right)} \right|}_{{{{k}^{2}} \to 0}}} = 1 - \frac{1}{6}r_{E}^{2}{{\vec {k}}^{2}},$

где r_E – зарядовый радиус ядра, ${{k}^{2}}~$ – четырех-импульс фотона. В результате для мюонного гелия имеем следующее выражение для поправки на структуру ядра:

(18)

${{V}_{{str}}} = - \frac{{2\pi {{\alpha }^{2}}}}{3}\tilde {r}_{{{\text{He}}}}^{2}\left( {{{e}_{1}}{{e}_{3}}{{\delta }^{3}}\left( {{{{\vec {r}}}_{{13}}}} \right) + {{e}_{1}}{{e}_{2}}{{\delta }^{3}}\left( {{{{\vec {r}}}_{{12}}}} \right)} \right),$

где ${{\tilde {r}}_{{{\text{He}}}}} = {{r}_{{{\text{He}}}}}{{m}_{e}}$ – зарядовый радиус ядра гелия. Все поправки представлены в электронных атомных единицах.

Релятивистские поправки, которые можно получить из гамильтониана Брейта, и их матричные элементы в случае трех взаимодействующих частиц:

(19)

$\begin{gathered} {{V}_{{rel}}} = - \frac{{{{\alpha }^{2}}}}{8}\sum\limits_{i = 1}^3 {\frac{{\vec {p}_{i}^{4}}}{{m_{i}^{3}}} - \frac{{\pi {{\alpha }^{2}}}}{2}} \sum\limits_{\begin{array}{*{20}{c}} {i,j = 1} \\ {i \ne j} \end{array}}^3 {{{e}_{i}}{{e}_{j}}\left( {\frac{1}{{m_{i}^{2}}} + \frac{1}{{m_{j}^{2}}}} \right)\delta \left( {{{{\vec {r}}}_{{ij}}}} \right)} - \\ - \,\,\frac{{{{\alpha }^{2}}}}{2}\sum\limits_{\begin{array}{*{20}{c}} {i,j = 1} \\ {i \ne j} \end{array}}^3 {\frac{{{{e}_{i}}{{e}_{j}}\left( {{{{\vec {p}}}_{i}}{{{\vec {p}}}_{j}} + \frac{{{{{\vec {r}}}_{{ij}}}\left( {{{{\vec {r}}}_{{ij}}} \cdot {{{\vec {p}}}_{i}}} \right){{{\vec {p}}}_{j}}}}{{r_{{ij}}^{2}}}} \right)}}{{{{m}_{i}}{{m}_{j}}{{r}_{{ij}}}}}} , \\ \end{gathered} $

где $\overrightarrow {{{p}_{i}}} $ – операторы импульсов частиц.

(20)

$\begin{gathered} \left\langle {{{\varphi }_{i}}} \right|\vec {p}_{1}^{4}\left| {{{\varphi }_{j}}} \right\rangle = \frac{{15~{{{\left( {2\pi } \right)}}^{3}}}}{{{{{\left( {{\text{det}}B} \right)}}^{{7{\text{/}}2}}}}} \times \\ \times \,\,\left[ {\left( {A_{{11}}^{j} + 2\frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{12}}^{j} + {{{\left( {\frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}} \right)}}^{2}}A_{{22}}^{j}} \right){\text{det}}{{A}^{i}} + } \right. \\ {{\left. { + \,\,\left( {A_{{11}}^{i} + 2\frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{12}}^{i} + {{{\left( {\frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}} \right)}}^{2}}A_{{22}}^{i}} \right){\text{det}}{{A}^{j}}} \right]}^{2}}, \\ \end{gathered} $

(21)

$\begin{gathered} \left\langle {{{\varphi }_{i}}} \right|\vec {p}_{2}^{4}\left| {{{\varphi }_{j}}} \right\rangle = \frac{{15~{{{\left( {2\pi } \right)}}^{3}}}}{{{{{\left( {{\text{det}}B} \right)}}^{{7{\text{/}}2}}}}} \times \\ \times \,\,\left[ {\left( {A_{{11}}^{j} - 2\frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{12}}^{j} + {{{\left( {\frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}} \right)}}^{2}}A_{{22}}^{j}} \right){\text{det}}{{A}^{i}} + } \right. \\ {{\left. { + \,\,\left( {A_{{11}}^{i} - 2\frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{12}}^{i} + {{{\left( {\frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}} \right)}}^{2}}A_{{22}}^{i}} \right){\text{det}}{{A}^{j}}} \right]}^{2}}, \\ \end{gathered} $

(22)

$\left\langle {{{\varphi }_{i}}} \right|\vec {p}_{3}^{4}\left| {{{\varphi }_{j}}} \right\rangle = \frac{{15~{{{\left( {2\pi } \right)}}^{3}}}}{{{{{\left( {{\text{det}}B} \right)}}^{{\frac{7}{2}}}}}}{{\left[ {A_{{22}}^{j}{\text{det}}{{A}^{i}} + A_{{22}}^{i}{\text{det}}{{A}^{j}}} \right]}^{2}},$

(23)

$\begin{gathered} \left\langle {{{\varphi }_{i}}\left| {\frac{1}{{{{r}_{{12}}}}}\left( {{{{\vec {p}}}_{1}}{{{\vec {p}}}_{2}} + \frac{{{{{\vec {r}}}_{{12}}}({{{\vec {r}}}_{{12}}}{{{\vec {p}}}_{1}}){{{\vec {p}}}_{2}}}}{{\vec {r}_{{12}}^{2}}}} \right)} \right|{{\varphi }_{j}}} \right\rangle = \frac{{8{{{(2\pi )}}^{{\frac{5}{2}}}}}}{{\sqrt {{{B}_{{22}}}} {{{(\det B)}}^{2}}}} \times \\ \times \,\,\left[ {\left( {A_{{11}}^{i} + \frac{{{{m}_{1}} - {{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{12}}^{i} - \frac{{{{m}_{1}}{{m}_{2}}}}{{{{{({{m}_{1}} + {{m}_{2}})}}^{2}}}}A_{{22}}^{i}} \right)\det {{A}^{j}} + \left( {A_{{11}}^{j} + \frac{{{{m}_{1}} - {{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{12}}^{j} - \frac{{{{m}_{1}}{{m}_{2}}}}{{{{{({{m}_{1}} + {{m}_{2}})}}^{2}}}}A_{{22}}^{j}} \right)\det {{A}^{i}}} \right], \\ \end{gathered} $

(24)

$\begin{gathered} \left\langle {{{\varphi }_{i}}\left| {\frac{1}{{{{r}_{{13}}}}}\left( {{{{\vec {p}}}_{1}}{{{\vec {p}}}_{3}} + \frac{{{{{\vec {r}}}_{{13}}}({{{\vec {r}}}_{{13}}}{{{\vec {p}}}_{1}}){{{\vec {p}}}_{3}}}}{{\vec {r}_{{13}}^{2}}}} \right)} \right|{{\varphi }_{j}}} \right\rangle = \frac{{8{{{(2\pi )}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}{{{{{(\det B)}}^{2}}\sqrt {{{B}_{{11}}} - 2\frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}{{B}_{{12}}} + {{{\left( {\frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}} \right)}}^{2}}{{B}_{{22}}}} }} \times \\ \times \,\,\left[ {\left( {\frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{22}}^{i} + A_{{12}}^{i}} \right)\det {{A}^{j}} + \left( {\frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{22}}^{j} + A_{{12}}^{j}} \right)\det {{A}^{i}}} \right], \\ \end{gathered} $

(25)

$\begin{gathered} \left\langle {{{\varphi }_{i}}\left| {\frac{1}{{{{r}_{{23}}}}}\left( {{{{\vec {p}}}_{2}}{{{\vec {p}}}_{3}} + \frac{{{{{\vec {r}}}_{{23}}}\left( {{{{\vec {r}}}_{{23}}}{{{\vec {p}}}_{2}}} \right){{{\vec {p}}}_{3}}}}{{\vec {r}_{{23}}^{2}}}} \right)} \right|{{\varphi }_{j}}} \right\rangle = \\ = \,\,\frac{{8{{{\left( {2\pi } \right)}}^{{5/2}}}}}{{{{{\left( {{\text{det}}B} \right)}}^{2}}\sqrt {{{B}_{{11}}} + 2\frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}{{B}_{{12}}} + {{{\left( {\frac{{{{m}_{1}}}}{{{{m}_{1}} + {{m}_{2}}}}} \right)}}^{2}}{{B}_{{22}}}} }} \times \\ \times \,\,\left[ {\left( {\frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{22}}^{i} - A_{{12}}^{i}} \right){\text{det}}{{A}^{j}} + \left( {\frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}A_{{22}}^{j} - A_{{12}}^{j}} \right){\text{det}}{{A}^{i}}} \right]. \\ \end{gathered} $

ЧИСЛЕННЫЙ РАСЧЕТ

Для численного расчета была написана программа в системе MATLAB для решения трехчастичной кулоновской задачи в рамках стохастического вариационного метода. За основу была взята программа из работы [11] на языке Фортран. При надлежащем выборе пробных функций данный метод может давать очень близкие к действительным значения. В том числе, если вид пробной функции с точностью до выбора параметров совпадает с точным решением, минимизация интеграла даeт точный результат. Выбор гауссовых функций в качестве базисных предпочтителен, так как они экспоненциально убывают с ростом расстояния между частицами, и при этом матричные элементы таких функций могут быть вычислены аналитически при условии, что матрица, составленная из нелинейных параметров A_ij, – положительно определенная. Тем не менее зачастую такого приближения оказывается недостаточно и приходится искать волновую функцию в виде линейной комбинации базисных функций (1), коэффициенты разложения которой, с точностью до нормировки, также рассматриваются как вариационные параметры. Однако в таком случае число варьируемых параметров начинает быстро расти с ростом числа базисных функций.

Нелинейные параметры A_ij генерируем следующим образом:

(26)

${{A}_{{ij}}} = \frac{1}{{{{{\left( {{{b}_{{min}}} + {{b}_{{max}}}x} \right)}}^{2}}}},$

где х – случайно генерируемое число в интервале (0, 1); b_min и b_max – заданные параметры. Для того чтобы наиболее компактно заполнить интервал, в котором подбираются нелинейные параметры, необходимо повторять данную процедуру большое число раз. Проблема состоит в том, что общая сложность решения задач вида (2), которая связана со временем выполнения задачи, составляет O(K³), и при увеличении размера базиса K в 2 раза, вычислительная сложность возрастает в среднем в 8 раз. Это очень замедляет работу метода и затрудняет перебор большого числа параметров. Чтобы повысить скорость вычисления, предлагаем поступать другим образом. Можно использовать результаты оптимизации параметров для базисов меньшего размера. Вместо непосредственного решения уравнения (2) с пробными функциями (1) строим итерационный процесс, постепенно увеличивая размерность базиса от 1 до K. На первой итерации пробная функция представляется в виде одной базисной. Для неe генерируется большой набор нелинейных параметров. Для каждого из этого набора решается задача (2) и определяется минимальная энергия. Набор параметров, дающий наименьшую энергию, сохраняется. На следующей итерации размерность базиса увеличивается на единицу, и новые наборы параметров генерируется только для новой базисной функции. В итоге на каждой n-ой итерации изменяются только параметры n-ой базисной функции, а для функций, успешно найденных на прошлых итерациях, меняются только коэффициенты разложения. Тем не менее скорость роста сложности остаeтся кубической и при больших размерах базиса скорость вычислений заметно снижается. Для того чтобы не решать задачу (2) с полностью заполненными матрицами заново на каждой итерации, можно также использовать результаты расчeтов, полученных на предыдущей итерации [15].

ЗАКЛЮЧЕНИЕ

В данной работе проведены исследования спектра энергии мюонного гелия. Для этого использовался не метод теории возмущений, как в предыдущей работе [17], а стохастический вариационный метод. В результате проведенных расчетов были получены следующие значения энергий связи мюонного гелия, поправки на структуру ядра (стр), релятивистской поправки (рел) и поправки на поляризацию вакуума (ПВ):

Полные значения энергий связи с учетом поправок имеют вид:

$\begin{gathered} E\left( {^{3}{\text{He}}\mu e} \right) = ~ - 10873.702742\,\,{\text{эВ}}, \\ E\left( {^{4}{\text{He}}\mu e} \right) = ~ - 10973.028228\,\,{\text{эВ}}. \\ \end{gathered} $

В сверхтонкой структуре спектра принято записывать вклады в МГц, и в результате наших расчетов получены следующие значения коэффициентов a, b, c и сверхтонких расщеплений основного состояния:

Полученные значения согласуются с [9, 16]. Имеющиеся расхождения связаны с меньшим размером базиса в наших расчетах и, как следствие, меньшей точностью энергии основного состояния. Численные результаты зависят от выбора исходных параметров, в том числе от масс частиц. Значения масс частиц в [9, 16] несколько отличаются от значений, рекомендованных КОДАТА [18], которые мы используем в расчетах. В работах [9, 16] расчет матричных элементов дельта-функций a, b, c, которые определяют сверхтонкое расщепление, выполнен с очень высокой точностью, достичь которую в рамках стохастического вариационного метода не удается при используемом нами размере базиса. Нам удалось получить совпадение c [9, 16] до пяти значащих цифр. Также необходимо отметить, что в работах [9, 16] при вычислении используется четверная точность, в то время как в наших расчетах используется двойная точность. Это также вносит различия в результаты.

Работа выполнена при финансовой поддержке РНФ (проект № 18-12-00128).

Список литературы

Pohl R., Antognini A., Nez F. et al. // Nature. 2010. V. 466. P. 213.
Antognini A., Nez F., Schuhmann K. et al. // Science. 2013. V. 339. P. 417.
Pohl R., Nez F., Fernandes M.P. et al. // Science. 2016. V. 353. P. 669.
Diepold M., Franke B., Krauth J.J. et al. // Ann. Phys. 2018. V. 396. P. 220.
Герштейн С.С., Петров Ю.В., Пономарев Л.И. // УФН. 1990. Т. 160. № 8. С. 3; Gershtein S.S., Petrov Yu.V., Ponomarev L.I. // Phys. Usp. 1990. V. 33. P. 591.
Dorokhov A.E., Kochelev N.I., Martynenko A.P. et al. // Eur. Phys. J. A. 2018. V. 54. P. 131.
Faustov R.N. Martynenko A.P., Martynenko F.A. et al. // Phys. Rev. A. 2015. V. 92. № 5. Art. № 052512.
Faustov R.N. Martynenko A.P., Martynenko F.A. et al. // Phys. Rev. A. 2014. V. 90. № 1. Art. № 012520.
Frolov A.M. // Phys. Lett. A. 2012. V. 376. P. 2548.
Korobov V.I., Puzynin I.V., Vinitsky S.I. // Phys. Lett. B. 1987. V. 196. P. 272.
Varga K., Suzuki Y. // Comp. Phys. Comm. 1997. V. 106. P. 157.
Eskin A.V., Korobov V.I., Martynenko A.P., Sorokin V.V. // EPJ Web Conf. 2019. V. 204. Art. № 05006.
Мартыненко А.П., Мартыненко Ф.А., Сорокин В.В. // Кр. сообщ. по физ. ФИАН. 2019. Т. 4. С. 54; Martynenko A.P., Martynenko F.A., Sorokin V.V. et al. // Bull. Lebedev Phys. Inst. 2019. V. 46. № 4. P. 143.
Korobov V.I., Martynenko A.P., Sorokin V.V., Eskin A.V. // Phys. Part. Nucl. 2019. V. 50. № 5. P. 633.
Suzuki Y., Varga K. Stochastic variational approach to quantum-mechanical few-body problems. Berlin: Springer, 1998. 478 p.
Aznabayev D.T., Bekbaev A.K., Korobov V.I. // Phys. Part. Nucl. Lett. 2018. V. 15. № 3. P. 236.
Krutov A.A., Martynenko A.P. // Phys. Rev. A. 2008. V. 78. Art. № 032513.
Mohr P.J., Newell D.B., Taylor B.N. // Rev. Mod. Phys. 2016. V. 88. Art. № 035009.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал