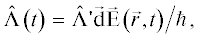Известия РАН. Серия физическая, 2020, T. 84, № 3, стр. 361-366

ВВЕДЕНИЕ

Фотонное эхо является одним из самых оптимальных методов для исследования процессов оптической дефазировки в различных средах, включая газы [1], жидкости [2], аморфные среды [3–5] и твердые тела [6, 7]. Первые эксперименты по спектроскопии фотонного эха проводили, как правило, в твердых телах – примесных кристаллах при криогенных температурах. Диапазон изучаемых длительностей оптической дефазировки ограничивался десятками наносекунд, что было связано с возможностями экспериментальной аппаратуры. Экспериментальные данные по фотонному эху в примесных кристаллах при криогенных температурах описывали в рамках простой Т₁–Т₂-модели, развитой Ф. Блохом, что позволяло измерять время наносекундной фазовой релаксации T₂, обусловленное квадратичным электрон-фононным ($\hat {W}{\text{ - }}$) взаимодействием.

Большой интерес для исследователей представляют структурно-неупорядоченные (аморфные) системы со сложной внутренней динамикой – полимеры, стекла, керамики. Отдельной важной задачей является исследование жидкостей и биологических сред, где важна возможность проведения измерений при нормальных (не криогенных) температурах. Отличия в динамике, наблюдаемой при таких условиях, от низкотемпературных экспериментов заключаются в проявлении линейного электрон-фононного $(\hat {V}{\text{ - }})$ взаимодействия, которое никак не может быть описано в рамках модели Блоха при помощи одного параметра T₂. Кроме того, оценки показывают, что характерные времена динамических процессов при таких условиях лежат в пико- и фемтосекундном диапазоне длительностей, что долгое время ограничивало возможности исследований методами оптической спектроскопии и фотонного эха. Ситуация кардинально изменилась с появлением фемтосекундных лазеров. История развития фемтосекундной лазерной техники и особенности ее использования для исследования быстропротекающих процессов в разных средах подробно описаны в монографии [8].

В связи с дороговизной фемтосекундной лазерной техники в 1980-х гг. появилась техника т.н. “некогерентного” фотонного эха [9]. В работах [10, 11] было показано, что широкополосное лазерное излучение может быть использовано для получения информации об ультракоротких временах фазовой релаксации. Однако предложенный авторами [11] и других похожих работ метод расчета учитывает в качестве параметров только длительность возбуждающих лазерных импульсов и величину T₂ и не принимает во внимание быстрые процессы, определяемые $\hat {V}$-взаимодействием при высоких температурах. Экспериментальные результаты, получаемые при измерении сигналов некогерентного фотонного эха в примесных твердотельных средах, весьма схожи с данными по фемтосекундному фотонному эху, полученными в тех же образцах. Однако могут наблюдаться и отличия, поскольку в сигнал некогерентного фотонного эха могут давать вклад процессы, протекающие за время длительности наносекундных возбуждающих лазерных импульсов, например, спектральная диффузия.

Практически сразу после появления первых экспериментальных результатов стало ясным, что быстрые кривые спада сигналов фемтосекундного и некогерентного фотонного эха не являются экспоненциальными и не описываются уравнениями Блоха. В работах И.С. Осадько, обобщенных в монографии [12], было введено понятие обобщенного вектора Блоха и развита теория когерентных оптических переходных процессов, позволяющая учитывать влияние процессов сверхбыстрой оптической дефазировки на формирование сигналов фемтосекундного фотонного эха. Отличительной особенностью данного подхода является одновременный учет квадратичного $\hat {W}$-взаимодействия, которое проявляется в экспериментах в виде экспоненциального затухания эха с характеристическим временем T₂, и $\hat {V}$-взаимодействия, описываемого быстрозатухающей функцией оптической дефазировки. Динамическая теория оптической дефазировки учитывает ширину σ оптической полосы поглощения хромофора, величину фактора Пекара–Хуанга φ(0, 0), частоту Дебая ν_D, а также другие характеристики среды и параметры эксперимента. Однако в расчетах возбуждающие лазерные импульсы полагали δ-образными и их реальную временную форму никак не учитывали. В данной работе теория дефазировки дополнена таким образом, чтобы учитывать форму ультракоротких лазерных импульсов, используемых для возбуждения сигналов фемтосекундного фотонного эха. В рамках развитого подхода каждый возбуждающий импульс представляется в виде последовательности δ-образных импульсов, распределенных таким образом, что их огибающая воспроизводит временную форму фемтосекундного лазерного импульса, известную из эксперимента. Особенно эффективным такой способ моделирования становится при расчете сигналов некогерентного фотонного эха, где широкополосные наносекундные импульсы представляют в виде последовательности пичков, длительность которых ограничена временем когерентности [10]. Развитый подход был апробирован на примере моделирования кривых спада сигналов фотонного эха, измеренных в экспериментах по фемтосекундному фотонному эху в примесной полимерной пленке и некогерентному фотонному эху в замороженном стекле.

ОСНОВНЫЕ УРАВНЕНИЯ МОДЕЛИ

В данном разделе мы следуем теории, развитой И.С. Осадько [12, 13]. Сигнал фотонного эха является эффектом 3-го порядка по полю. Амплитуда сигнала определяется наведенным дипольным моментом образца, который вычисляется как сумма по всем молекулам образца:

где функция распределения частот отдельных хромофоров по неоднородно-уширенному спектру поглощения $N\left( {\Omega } \right)$ определяет форму оптической полосы поглощения образца. Для упрощения расчета будет рассмотрен гауссов контур с шириной $\sigma .$ Наведенная поляризация молекулы ${{d}_{{3PE}}}\left( t \right) = \vec {d}{{\vec {\rho }}_{3}}\left( t \right),$ где

Здесь $\vec {d}$ – дипольный момент молекулы, $\vec {\rho }\left( t \right)$ – обобщенный вектор Блоха, ${{e}^{{\hat {E}t}}}$ – оператор релаксации.

Матрица ${\hat {\Lambda }}\left( t \right)$ взаимодействия хромофора с электромагнитным полем лазерных импульсов может быть представлена в виде

где ${\hat {\Lambda }'}$ не зависит от времени. В случае, если импульсы δ-образные, где $\tau $ – временной интервал между первым и вторым, а ${{t}_{w}}$ – между вторым и третьим импульсами, ${{\vec {n}}_{i}}$ – единичный вектор в направлении распространения i-го лазерного импульса.

Наведенная поляризация молекулы, возбуждаемой тремя δ-образными импульсами, формирующая сигнал фотонного эха, определяется следующей формулой:

где

$\tau {\kern 1pt} '$ – интервал между моментами времени $t$ регистрации сигнала и третьего лазерного импульса. Формула (6в), содержащая два слагаемых, полностью описывает оптическую дефазировку. Первое слагаемое определяет вклад $\hat {W}$-взаимодействия, которое проявляется в кривых затухания сигналов фотонного эха в виде длинного экспоненциального спада с характеристическим временем T₂, а в оптических спектрах – в виде узких бесфононных линий (БФЛ). Второе слагаемое – функция быстрой оптической дефазировки, обусловленной $\hat {V}$-взаимодействием. Она описывает ультрабыстрое затухание эхо-сигнала в области малых временных задержек между возбуждающими импульсами, проявляясь в спектре в виде широкого фононного крыла (ФК). Функция дефазировки

где $~n\left( \nu \right) = {{\left[ {{{e}^{{{{h{\nu }} \mathord{\left/ {\vphantom {{h{\nu }} {kT}}} \right. \kern-0em} {kT}}}}} - 1} \right]}^{{ - 1}}},$ а $\varphi \left( \nu \right)$ – функция взвешенной плотности фононных состояний. В квазидебаевской модели $\varphi \left( \nu \right) \propto \varphi \left( {0,0} \right){{\left( {\frac{\nu }{{{{\nu }_{D}}}}} \right)}^{{3~}}}{{\left( {1 - \frac{\nu }{{{{\nu }_{D}}}}} \right)}^{{2~}}},$ где ${{\nu }_{D}}$ – граничная дебаевская частота, $\varphi \left( {0,0} \right)$ – фактор Пекара–Хуанга при нулевой температуре, связанный с фактором Дебая–Валлера $\alpha $(0) соотношением $\varphi \left( {0,0} \right)$ = $ - \ln {\alpha }\left( 0 \right).$

Для того, чтобы учесть ненулевую длительность лазерных импульсов, представим каждый из них в виде суммы δ-образных пичков: $\sum {{c}_{i}}{{\delta }_{i}}\left( t \right),$ где ${{\delta }_{i}}\left( t \right)$ = $\delta \left( {t - {{t}_{i}}} \right).$ Амплитуда ${{c}_{i}}$ и момент времени ${{t}_{i}}$ для каждого пичка подбираются таким образом, чтобы огибающая их суммы воспроизводила временную форму возбуждающего лазерного импульса. Отметим, что форму лазерного импульса можно измерить и связать расчет с реальными параметрами эксперимента. Как правило, рассматривается гауссов контур с шириной $\Delta t.$

Используя формулы (2) и (4) и суммируя вклады от всех комбинаций подимпульсов, которые создают волну поляризации образца в направлении распространения эхо-отклика, после интегрирования по частоте неоднородного контура получается конечное выражение для вычисления интенсивности сигнала фотонного эха:

где ${{t}_{i}}$ – моменты времени для пичков, составляющих первый, а ${{t}_{j}}$ и ${{t}_{k}}$ – второй и третий импульсы, ${\theta }\left( x \right)$ – функция Хевисайда.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Фемтосекундное фотонное эхо исследовали в полимерной пленке поливинилбутираля, допированной молекулами фталоцианина при разных температурах [14]. Эксперименты были выполнены в лаборатории быстропротекающих молекулярных процессов Казанского физико-технического института им. Е.К. Завойского на фемтосекундном эхо-спектрометре.

Характерный вид кривых спада при комнатной температуре и при температуре жидкого азота показан на рис. 1a. Значения времени фазовой релаксации T₂ (180 фc при 300 K и 240 фc при 77 K) были определены по методике, описанной в [11]. Отметим, что для описания измеренных неэкспоненциальных кривых спада авторами была использована теория, учитывающая только один параметр T₂ и форму возбуждающих лазерных импульсов.

Для расчета кривых спада в рамках развитого подхода нами были использованы параметры, известные из описания эксперимента [14]: φ(0, 0) = = 0.16, ν_D = 10¹² c^–1, σ = 370 см^–1, Δt = 95 фс. Результаты расчета показаны на рис. 1б. Видно, что расчетные кривые хорошо воспроизводят экспериментальные данные, однако моделирование дает значение T₂ (300 K) = 180 фс.

Рассмотрим экспериментальные результаты по некогерентному фотонному эху в замороженном толуоле с примесью молекул цинк-октаэтилпорфина (Zn-ОЭП) [4, 15]. Измерения были выполнены в лаборатории электронных спектров молекул Института спектроскопии Российской академии наук. Широкий температурный диапазон измерений позволил проследить перераспределение вкладов БФЛ и ФК в оптическую дефазировку с ростом температуры вплоть до температуры Дебая для толуола (около 100 К). Кривые спада сигналов двухимпульсного некогерентного фотонного эха, измеренные при разных температурах – 7, 30 и 100 К, показаны на рис. 2 (а–в). Видно, что с ростом температуры уменьшается вклад в кривую спада БФЛ – исчезает длинный спад, и форма кривой становится симметричной, что означает доминирование вклада ФК при высоких температурах. Результаты расчета показаны на рис. 2 (г–е). Для расчета кривых спада были использованы следующие значения параметров: φ(0, 0) = 0.02, ν_D = 2 · 10¹² c^–1, σ = 400 см^–1, Δt = = 200 фс (параметры взяты из описания экспериментов [4, 15], а величина Δt оценена как время когерентности излучения по ширине спектра широкополосных лазерных импульсов), г) T = 7 K, T₂ = 5.4 · 10^–11 c; д) T = 30 K, T₂ = 3.1 · 10^–12 c, е) T = = 100 K, T₂ = 2.2 · 10^–12 c. Видно, что расчетные кривые хорошо воспроизводят экспериментальные данные и позволяют описать наблюдаемую трансформацию кривых спада, связанную с изменением соотношения вкладов БФЛ и ФК в кривую спада, причем расчет проведен с учетом реальных характеристик примесной среды и известных параметров эксперимента. Экспериментальные и расчетные значения T₂ близки.

ЗАКЛЮЧЕНИЕ

Развитый на основе динамической теории оптической дефазировки подход позволяет учитывать временную форму ультракоротких лазерных импульсов при расчете когерентных оптических откликов типа фотонного эха. Возможности метода продемонстрированы на примере моделирования ультрабыстрых кривых спада, измеренных в экспериментах по фемтосекундному и некогерентному фотонному эху. При моделировании сигналов некогерентного фотонного эха широкополосные наносекундные лазерные импульсы описываются последовательностью ${\delta }$-образных импульсов, которые распределены по гауссовому контуру. Длительность такого составного гауссового импульса равна времени когерентности, которое соответствует обратной спектральной ширине некогерентного лазерного импульса [10]. Такой подход, позволяющий не учитывать наносекундную длительность некогерентных лазерных импульсов, в данном случае оправдан, поскольку согласно модели аккумулированного фотонного эха идентичные пары импульсов приводят только к росту амплитуды суммарного отклика, не влияя на его временную форму и параметры оптической дефазировки. Результаты расчета качественно воспроизводят экспериментальные данные, однако используемые при моделировании упрощения не могут не проявиться при прямом количественном сопоставлении результатов. Обнаруженные различия, в частности, отсутствие временного сдвига максимума кривой спада, наблюдаемое в эксперименте, по-видимому, обусловлены такими приближениями. Кроме того, развитая модель была использована для вычисления фактора Дебая–Валлера – параметра, описывающего температурное изменение формы оптической полосы для исследуемых систем.

Работа выполнена при финансовой поддержке РФФИ (проект № 18-02-01121а).