Известия РАН. Серия физическая, 2020, T. 84, № 3, стр. 407-412

ВВЕДЕНИЕ

Задача создания ярких источников неклассических состояний в оптике, включаеющая разработку генераторов однофотонных состояний, а также создание источников перепутанных фотонов, может быть эффективно решена с использованием плазмонных медиаторов [1] и нелинейных спазеров [2]. В самом простом случае спазер [3] состоит из связанных ближним полем полупроводниковой квантовой точки (КТ) и металлической наночастицы (НЧ). КТ выступает здесь в качестве эффективной накачки, поскольку в процессе распада имеющихся в ней экситонов происходит возмущение ближнего поля КТ. При соблюдении условий плазмон-экситонного резонанса это возмущение приводит к возбуждению плазмонов, локализованных на поверхности металлической НЧ. В настоящей работе предложена модель спазера, в котором реализуется конфигурация из трех нанобъектов НЧ–КТ–НЧ, расположенных вдоль одной прямой. Нелинейный режим работы рассматриваемого устройства [4, 5] подразумевает значительную разность в значениях частот плазмонного резонанса ${{\omega }_{p}}$ в НЧ и энергии перехода $\omega $ в КТ при фиксированном значении спазерной частоты $\bar {\omega }.$ Тогда в зависимости от соотношения частот отстроек ${{\delta }_{{}}} = \bar {\omega } - \omega $ и $\Delta = \bar {\omega } - {{\omega }_{p}}$ в системе возможна реализация условий для четырехчастичных процессов плазмон-плазмонного рассеяния (когда $\delta \gg \Delta $), составляющего основу нелинейной наноплазмоники [6]. Также в системе возможно плазмон-экситонное рассеяние [7] и нелинейные двухквантовые переходы [8] при эффективном распаде биэкситонных пар [9], когда $\delta \ll \Delta .$ В практическом плане последний режим интересен возможностью генерации биплазмонных перепутанных пар [10], которые могут использоваться для осуществления протоколов квантовой обработки информации. В излучающем режиме подобные спазерные системы могут служить эффективными наноисточниками неклассического поля для флуоресцентной спектромикроскопии высокого разрешения [11, 12], являющейся одним из наиболее востребованных направлений современной экспериментальной спектроскопии как в РФ, так и за рубежом.

Предварительная настройка различных режимов взаимодействия в спазере может быть осуществлена путем варьирования размеров и материала КТ и НЧ. Последующее “ручное” управление режимами может быть осуществлено методами современной спинтроники [13], в частности, – при использовании магнитного поля для формирования зеемановской структуры энергетических уровней КТ. В перспективе на основе таких отдельных функциональных звеньев – спазеров – путем масштабирования может быть создано более сложное устройство для квантовой обработки информации, носителями которой являются локализованные плазмоны.

МОДЕЛЬ НЕЛИНЕЙНЫХ БЛИЖНЕПОЛЕВЫХ ПЛАЗМОН-ЭКСИТОННЫХ ВЗАИМОДЕЙСТВИЙ В СИСТЕМЕ МНОГОЧАСТИЧНОГО СПАЗЕРА

Нелинейные режимы взаимодействия между НЧ и КТ, а также с плазмонами НЧ соседних спазеров в цепочке реализуются, когда отстройки $\delta $ и $\Delta $ начинают существенно превышать скорости спонтанной релаксации, а также частоты Раби для соответствующих процессов. Так, условием формирования биэкситонных состояний [14] в спазере может служить неравенство $\left| \delta \right| > {{\Omega }_{{1,2}}},$ $\left| \Delta \right|$ аналогично известным нелинейным эффектам в оптике [15, 16]. В предлагаемой схеме взаимодействия осуществляются между одной КТ и парой НЧ посредством ближнего поля, как на рис. 1. При этом базисные состояния ${{\left| g \right\rangle }_{1}}$ = = $\left| {1S\left( h \right),{{m}_{s}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}} \right\rangle ,$ ${{\left| g \right\rangle }_{2}}$ = $\left| {1S\left( h \right),{{m}_{s}} = {{ + 1} \mathord{\left/ {\vphantom {{ + 1} 2}} \right. \kern-0em} 2}} \right\rangle ,$ ${{\left| e \right\rangle }_{1}}$ = = $\left| {1S\left( e \right),{{m}_{s}} = {{ + 1} \mathord{\left/ {\vphantom {{ + 1} 2}} \right. \kern-0em} 2}} \right\rangle ,$ ${{\left| e \right\rangle }_{2}}$ = $\left| {1S\left( e \right),{{m}_{s}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}} \right\rangle $ для электронов и дырок КТ различаются значениями магнитного квантового числа ${{m}_{s}},$ а формируемый на их основе биэкситон ${{\hat {S}}^{ + }}$ соответствует состоянию $XX$ с частотой ${{\omega }_{{XX}}} = {{\omega }_{{{{X}_{ - }}}}}$ + ${{\omega }_{{{{X}_{ + }}}}} - {{\Delta }_{{2b}}},$ ${{\Delta }_{{2b}}}$ – энергия связи биэкситона, при этом плазмоны описываются операторами рождения $\hat {c}_{1}^{ + }$ и $\hat {c}_{2}^{ + }$ с немного различающимися энергиями для различных промежуточных уровней ${{X}_{ + }}$ (${{X}_{ - }}$) с частотами ${{\omega }_{{{{X}_{ + }}}}}$ (${{\omega }_{{{{X}_{ - }}}}}$).

Управление параметрами биэкситонного состояния может быть осуществлено при наличии внешнего магнитного поля ${{\vec {B}}_{m}}$ в геометрии Фойгта, которое приводит к смещению энергетических уровней на величину ${{\Delta }_{m}} = {{{{g}^{F}}{{\mu }_{B}}{{B}_{m}}} \mathord{\left/ {\vphantom {{{{g}^{F}}{{\mu }_{B}}{{B}_{m}}} \hbar }} \right. \kern-0em} \hbar },$ где ${{\mu }_{B}} = 9.27 \cdot {{10}^{{ - 24}}}$ Дж ∙ Тл^–1, ${{g}^{F}}$ – фактор Ланде. Параметр ${{g}^{F}}$ существенно зависит от радиуса ${{a}_{{{\text{КТ}}}}}$ КТ [17], при малых значениях практически совпадая с $g_{e}^{F} = 2$ для свободного электрона и уменьшаясь до величины $g_{{CdSe}}^{F} = 0.68$ [18] для массивного полупроводника CdSe. Процессу формирования пары плазмонов при высвечивании биэкситона должна соответствовать характерная частота Раби ${{\Omega }^{{\left( 2 \right)}}} = {{{{\Omega }_{1}} \cdot {{\Omega }_{2}}} \mathord{\left/ {\vphantom {{{{\Omega }_{1}} \cdot {{\Omega }_{2}}} {\left( {2\left| \delta \right|} \right)}}} \right. \kern-0em} {\left( {2\left| \delta \right|} \right)}}$ для двухчастичного перехода, где ${{\Omega }_{{1\left( 2 \right)}}}$ = ${{{{\mu }_{{{\text{КТ}}}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{{\text{КТ}}}}}} {{{r}^{3}}}}} \right. \kern-0em} {{{r}^{3}}}}\sqrt {{{{{\omega }_{{p1\left( 2 \right)}}}a_{{{\text{НЧ}}1\left( 2 \right)}}^{3}} \mathord{\left/ {\vphantom {{{{\omega }_{{p1\left( 2 \right)}}}a_{{{\text{НЧ}}1\left( 2 \right)}}^{3}} {\left( {2\pi {{\varepsilon }_{0}}\hbar } \right)}}} \right. \kern-0em} {\left( {2\pi {{\varepsilon }_{0}}\hbar } \right)}}} $ с учетом дипольного момента ${{\mu }_{{{\text{НЧ}}}}}$ = $\sqrt {2{{\varepsilon }_{0}}\hbar a_{{{\text{НЧ}}}}^{3}{{\omega }_{p}}} $ для наночастиц. Тогда гамильтониан, соответствующий модели на рис. 1, приобретает вид:

где два слагаемых в скобках задают процессы биэкситонного высвечивания с формированием соответствующих плазмонных пар. Здесь параметр $D = {{\hat {S}}^{ + }}\hat {S} - \hat {S}{{\hat {S}}^{ + }}$ соответствует оператору разности населенности между соответствующими уровнями при рождении (уничтожении) биэкситона. Полагаем, что обе НЧ являются идентичными, т.е. ${{\omega }_{{p1}}} = {{\omega }_{{p2}}} = {{\omega }_{p}},$ а взаимодействием между удаленными НЧ, находящимися на расстоянии $2r,$ в задаче можно пренебречь. В отсутствие внешнего магнитного поля полагаем, что ${{\omega }_{{{{X}_{ - }}}}} = {{\omega }_{{{{X}_{ + }}}}} = {{\omega }_{X}}.$ Тогда соответствующую гамильтониану (1) систему уравнений Гейзенберга–Ланжевена можно представить в следующей форме:

где скорости затухания плазмонов положены равными, а накачка ${{D}_{0}}$ является распределенной величиной, осуществляемой со скоростью ${1 \mathord{\left/ {\vphantom {1 {{{\tau }_{D}}}}} \right. \kern-0em} {{{\tau }_{D}}}};$ ${{\hat {F}}_{{c1\left( {c2} \right)}}},$ ${{\hat {F}}_{S}},$ ${{\hat {F}}_{D}}$ представляют собой операторы ланжевеновского шума для соответствующих мод, которые вводятся феноменологически, ${{\delta }^{{\left( 2 \right)}}} = 2\bar {\omega } - {{\omega }_{{XX}}}.$ При выводе системы (2) использовалось приближение медленно меняющихся амплитуд: ${{\hat {c}}_{1}} = {{\hat {c}}_{1}}{{e}^{{ - i\bar {\omega }t}}},$ ${{\hat {c}}_{2}} = {{\hat {c}}_{2}}{{e}^{{ - i\bar {\omega }t}}}$ и $\hat {S} = \hat {S}{{e}^{{ - 2i\bar {\omega }t}}}.$

Сначала определим новые условия генерации для нелинейного спазера, заменяя операторы системы (2) С-числами и переходя к системе алгебраических тождеств для стационарного режима его работы:

где введены новые обозначения ${{A}_{1}} = i\Delta - \tau _{c}^{{ - 1}}$ и B₁ = = $i{{\delta }^{{\left( 2 \right)}}} - \tau _{S}^{{ - 1}}.$ Уравнения для плазмон-экситонных мод можно получить, выражая $S$ из (3в) и подставляя в (3а) и (3б). В окончательном виде такие уравнения имеют вид:

Частота спазирования может быть найдена из уравнений (4а) и (4б), согласно которым выражение ${{A}_{1}}{{B}_{1}}$ должно всегда принимать действительные значения. Поскольку ${{A}_{1}}{{B}_{1}} = {1 \mathord{\left/ {\vphantom {1 {\left( {{{\tau }_{c}}{{\tau }_{S}}} \right)}}} \right. \kern-0em} {\left( {{{\tau }_{c}}{{\tau }_{S}}} \right)}} - \Delta {{\delta }^{{\left( 2 \right)}}}$ – $ - \,\,i\left( {{\Delta \mathord{\left/ {\vphantom {\Delta {{{\tau }_{S}}}}} \right. \kern-0em} {{{\tau }_{S}}}} + {{{{\delta }^{{\left( 2 \right)}}}} \mathord{\left/ {\vphantom {{{{\delta }^{{\left( 2 \right)}}}} {{{\tau }_{c}}}}} \right. \kern-0em} {{{\tau }_{c}}}}} \right),$ выявленное ограничение выполняется в случае

при этом $\operatorname{Re} \left( {{{A}_{1}}{{B}_{1}}} \right) > 0.$ Соотношение (3г), в частности, будет выполняться при условиях ${{\delta }^{{\left( 2 \right)}}} < 0$ и $\Delta > 0.$ Наличие управляющего магнитного поля в рассматриваемой модели приводит к новым выражениям для частотных отстроек в форме ${{\delta }_{{1,2}}} = \bar {\omega } - {{\omega }_{{{{X}_{ - }},{{X}_{ + }}}}}$ и ${{\delta }^{{\left( 2 \right)}}} = 2\bar {\omega }$ – ${{\omega }_{{XX0}}} - 2kB_{m}^{2},$ ${{\omega }_{{{{X}_{ - }},{{X}_{ + }}}}}$ = = ${{\omega }_{{X0}}} \mp \alpha {{B}_{m}} + kB_{m}^{2},$ с учетом которых частота спазирования $\bar {\omega }$ примет вид: где ${{\omega }_{{XX0}}} = {{\left. {{{\omega }_{{XX}}}} \right|}_{{{{B}_{m}} = 0}}},$ ${{\omega }_{{X0}}} = {{{{\omega }_{p}} + {{\Delta }_{{2b}}}} \mathord{\left/ {\vphantom {{{{\omega }_{p}} + {{\Delta }_{{2b}}}} 2}} \right. \kern-0em} 2},$ ω_XX = ω_XX0 + + $2kB_{m}^{2},$ $\alpha = {{{{g}^{F}}{{\mu }_{B}}} \mathord{\left/ {\vphantom {{{{g}^{F}}{{\mu }_{B}}} \hbar }} \right. \kern-0em} \hbar },$ $k = {{{{e}^{2}}a_{{ex}}^{2}} \mathord{\left/ {\vphantom {{{{e}^{2}}a_{{ex}}^{2}} {\left( {4\hbar {\mu *}} \right)}}} \right. \kern-0em} {\left( {4\hbar {\mu *}} \right)}}.$ Параметры ${\mu }* = {{\left( {{1 \mathord{\left/ {\vphantom {1 {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}} + {1 \mathord{\left/ {\vphantom {1 {{{m}_{h}}}}} \right. \kern-0em} {{{m}_{h}}}}} \right)}^{{ - 1}}}$ и ${{a}_{{ex}}} = \sqrt {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}\left( {r_{e}^{2} + r_{h}^{2}} \right)} $ определяются массой и радиусом экситона, где ${{r}_{e}}$ и ${{r}_{h}}$ – эффективные радиусы электрона и дырки соответственно.

С учетом зависимости для энергии перехода [19] реализация нелинейного режима в спазере возможна при выборе КТ, размер которых заведомо больше, чем необходимо для установления плазмонного резонанса в системе.

Для нахождения стационарных значений ${{\bar {с}}_{i}},$ $\bar {S}$ и $\bar {D}$ необходимо решить систему (2) относительно C-чисел ${{с}_{i}},$ $S$ и $D$. В частности, из уравнений (3а) и (3б) можно получить выражения вида $\bar {c}_{2}^{*}S = {{{{A}_{1}}{{{\bar {c}}}_{1}}} \mathord{\left/ {\vphantom {{{{A}_{1}}{{{\bar {c}}}_{1}}} {\left( {i{{\Omega }^{{\left( 2 \right)}}}} \right)}}} \right. \kern-0em} {\left( {i{{\Omega }^{{\left( 2 \right)}}}} \right)}}$ и $\bar {c}_{1}^{*}S = {{{{A}_{1}}{{{\bar {c}}}_{2}}} \mathord{\left/ {\vphantom {{{{A}_{1}}{{{\bar {c}}}_{2}}} {\left( {i{{\Omega }^{{\left( 2 \right)}}}} \right)}}} \right. \kern-0em} {\left( {i{{\Omega }^{{\left( 2 \right)}}}} \right)}},$ при подстановке которых в уравнение (3г) амплитуда плазмонов для стационарного случая приобретает вид:

и определена с точностью до фазы плазмонов ${{\phi }_{i}}.$ При подстановке выражений (7) в уравнение (3в) получим амплитуду экситонной моды $\bar {S}$ в виде $\bar {S} = - {{i{{\Omega }^{{\left( 2 \right)}}}{{\tau }_{c}}} \mathord{\left/ {\vphantom {{i{{\Omega }^{{\left( 2 \right)}}}{{\tau }_{c}}} {\left( {4{{B}_{1}}{{\tau }_{D}}} \right)}}} \right. \kern-0em} {\left( {4{{B}_{1}}{{\tau }_{D}}} \right)}}\bar {D}\left( {{{D}_{0}} - \bar {D}} \right){{e}^{{i\left( {{{\phi }_{1}} + {{\phi }_{2}}} \right)}}}.$ Подставляя (7) в (4)–(5), получим уравнение для разности населенностей в форме: ${{\bar {D}}^{2}} - \bar {D}{{D}_{0}}$ + + ${{4{{\tau }_{D}}} \mathord{\left/ {\vphantom {{4{{\tau }_{D}}} {\left( {{{\Omega }^{{\left( 2 \right)}}}^{2}{{\tau }_{c}}} \right)}}} \right. \kern-0em} {\left( {{{\Omega }^{{\left( 2 \right)}}}^{2}{{\tau }_{c}}} \right)}}\left( {{{{\left( {{{\tau }_{c}}{{\tau }_{S}}} \right)}}^{{ - 1}}} - \Delta {{\delta }^{{\left( 2 \right)}}}} \right) = 0.$ Уравнение имеет два корня, из которых только один является устойчивым. Соответствующее устойчивое решение имеет вид

Для дальнейшего моделирования размер КТ CdSe и золотых НЧ выберем равными ${{D}_{{{\text{КТ}}}}} = 2{{a}_{{{\text{НЧ}}}}}$ = = ${\text{4}}{\text{.612}}\,\,{\text{нм}}{\text{.}}$ Для золотых НЧ ${{\lambda }_{p}} = 520\,\,{\text{нм}}$ и для КТ CdSe ${{\Delta }_{{2b}}} = 3.093 \cdot {{10}^{{14}}}\,\,{{{\text{c}}}^{{ - 1}}}$ (0.204 эВ). Дипольный момент соответствующего перехода в КТ будет составлять ${{\mu }_{{{\text{КТ}}}}}$ = $0.303 \cdot {{10}^{{ - 28}}}\,\,{\text{Кл}} \cdot {\text{м}}{\text{.}}$ При выборе значений параметров ${{\tau }_{c}} = 5 \cdot {{10}^{{ - 12}}}\,\,{\text{с}}$ и ${{\tau }_{S}} = 4 \cdot {{10}^{{ - 11}}}\,\,{\text{с}}$ и с учетом ${{B}_{m}} = 0\,\,{\text{Тл}}$ величины отстроек составят $\delta _{0}^{{\left( 2 \right)}} = 0\,\,{{{\text{с}}}^{{ - 1}}}$ и ${{\delta }_{0}}$ = $ - 1.547 \cdot {{10}^{{14}}}\,\,{{{\text{с}}}^{{ - 1}}}.$ Полагая, что расстояние между НЧ и КТ составляет $r = 5.12\,\,{\text{нм,}}$ частота Раби $\Omega \equiv {{\Omega }_{1}} = {{\Omega }_{2}}$ одночастичных экситон-плазмонных переходов составит величину $\Omega = 2.012 \cdot {{10}^{{13}}}\,\,{{{\text{с}}}^{{ - 1}}},$ тогда как ${{\Omega }^{{\left( 2 \right)}}}$ двухчастичных переходов становится равной ${{\Omega }^{{\left( 2 \right)}}}$ = = $2.617 \cdot {{10}^{{12}}}\,\,{{{\text{c}}}^{{ - 1}}}.$ Таким образом, выполняется условие $\Omega > {{\Omega }^{{\left( 2 \right)}}},$ однако мы не рассматриваем слагаемые с $\Omega $ в модели (1).

Наличие внешнего магнитного поля в области нахождения КТ приводит к снятию вырождения спазера НЧ–КТ–НЧ по частоте и возможности сравнительно простого управления его частотными характеристиками (рис. 1в). Так, при величине фактора Ланде $g_{{CdSe}}^{F} = 1.71$ для КТ CdSe заданного размера и ${{B}_{m}} = 5\,\,{\text{Тл}}$ диамагнитный сдвиг составит $kB_{m}^{2}$ = $3.66 \cdot {{10}^{{11}}}\,\,{{{\text{с}}}^{{ - 1}}},$ а зеемановский сдвиг составит $\alpha {{B}_{m}}$ = $ \pm 7.51 \cdot {{10}^{{11}}}\,\,{{{\text{с}}}^{{ - 1}}}.$ С учетом полученного решения (6) спазерная частота $\bar {\omega } = 3.625 \cdot {{10}^{{15}}}\,\,{{{\text{с}}}^{{ - 1}}}$ (${{\delta }_{1}}$ = $ - 1.539 \cdot {{10}^{{14}}}\,\,{{{\text{с}}}^{{ - 1}}},$ ${{\delta }_{2}}$ = = $ - 1.554 \cdot {{10}^{{14}}}\,\,{{{\text{с}}}^{{ - 1}}},$ $\Delta = 3.445 \cdot {{10}^{{11}}}\,\,{{{\text{с}}}^{{ - 1}}},$ δ⁽²⁾ = –4.306 · · 10¹⁰ с^–1, ${{\omega }_{p}} = 3.625 \cdot {{10}^{{15}}}\,\,{{{\text{с}}}^{{ - 1}}}$).

При выборе величины внешней накачки D₀ = 0.5 с обратной скоростью ${{\tau }_{D}} = 6.2 \cdot {{10}^{{ - 13}}}{\text{c}}$ полученное с помощью (8) стационарное решение для инверсии населённости составит $\bar {D} = 0.0029.$ Прямое численное моделирование, полученной после усреднения системы уравнений (2), демонстрирует выход к найденным стационарным решениям на характерном временном интервале 20 пс при выбранных параметрах. При этом кривые усиления для числа плазмонов проявляют сугубо нелинейное поведение (рис. 2). На первом участке действие накачки приводит только к линейному росту разности населенности, а среднее число плазмонов ${{\left| {{{{\bar {c}}}_{1}}} \right|}^{2}}$ остается равным нулю. При достижении накачкой порогового значения ${{D}_{0}} = {{D}_{{th}}} = 0.0762$ возникает разрыв первого рода со скачкообразным изменением разности населённостей и среднего числа плазмонов. Дальнейшее увеличение накачки приводит к росту числа плазмонов с одновременным уменьшением разности населённости.

ГЕНЕРАЦИЯ ПЕРЕПУТАННЫХ КВАНТОВЫХ СОСТОЯНИЙ В СПАЗЕРНЫХ СИСТЕМАХ

Далее проследим за динамикой параметров, которые описывают корреляционные свойства фотонов, испускаемых спазерной системой (рис. 1) в режиме выше порога генерации. Оператор фотонов, регистрируемых в дальней зоне, можно представить в виде ${{\hat {f}}_{i}} = {{\mu }_{{{\text{НЧ}}}}}\hat {c}_{i}^{ + } + {{\mu }_{{{\text{КТ}}}}}{{\hat {S}}^{ + }}$ [2], где ${{\mu }_{{{\text{НЧ}}}}}$ = $2.94 \cdot {{10}^{{ - 28}}}\,\,{\text{Кл}} \cdot {\text{м}}{\text{.}}$ С выбранными параметрами справедливо неравенство ${{\mu }_{{{\text{НЧ}}}}}\left\langle {\hat {c}_{i}^{ + }} \right\rangle > {{\mu }_{{{\text{КТ}}}}}\left\langle {{{{\hat {S}}}^{ + }}} \right\rangle $ $\left( {{{{{\mu }_{{{\text{НЧ}}}}}\left\langle {\hat {c}_{i}^{ + }} \right\rangle } \mathord{\left/ {\vphantom {{{{\mu }_{{{\text{НЧ}}}}}\left\langle {\hat {c}_{i}^{ + }} \right\rangle } {\left( {{{\mu }_{{{\text{КТ}}}}}\left\langle {{{{\hat {S}}}^{ + }}} \right\rangle } \right)}}} \right. \kern-0em} {\left( {{{\mu }_{{{\text{КТ}}}}}\left\langle {{{{\hat {S}}}^{ + }}} \right\rangle } \right)}} = 99.21} \right),$ поэтому в работе мы принимаем ${{\hat {f}}_{i}} \cong {{\mu }_{{{\text{НЧ}}}}}\hat {c}_{i}^{ + }.$ Тогда соответствующий кросс-корреляционной функции параметр $G_{{12}}^{{(2)}}\left( {t,\tau } \right)$ = $\frac{{\left\langle {\hat {c}_{1}^{ + }\left( t \right){{{\hat {c}}}_{1}}\left( t \right)\hat {c}_{2}^{ + }\left( {t + \tau } \right){{{\hat {c}}}_{2}}\left( {t + \tau } \right)} \right\rangle }}{{\left\langle {\hat {c}_{1}^{ + }\left( t \right){{{\hat {c}}}_{1}}\left( t \right)} \right\rangle \left\langle {\hat {c}_{2}^{ + }\left( {t + \tau } \right){{{\hat {c}}}_{2}}\left( {t + \tau } \right)} \right\rangle }}$ будет являться критерием установления неклассических корреляций между оптическими модами, связанными с соответствующими операторами плазмонов ${{\hat {с}}_{1}}$ и ${{\hat {с}}_{2}}.$ В частности, условие $G_{{12}}^{{(2)}} > 1$ связывают с межмодовой группировкой фотонов. Вместе с тем нарушение неравенства Коши–Шварца $C \equiv \frac{{G_{{12}}^{{\left( 2 \right)}}{{{\left( {t,0} \right)}}^{2}}}}{{g_{1}^{{\left( 2 \right)}}\left( {t,0} \right)g_{2}^{{\left( 2 \right)}}\left( {t,0} \right)}} \leqslant 1$ сигнализирует о появлении неклассических корреляций, а также о перепутывании между фотонами различных мод, где $g_{i}^{{\left( 2 \right)}}\left( {t,0} \right)$ = $G_{i}^{{\left( 2 \right)}}\left( {t,0} \right) + 1,$ $i = 1,2,$ а автокорреляционная функция имеет вид $G_{i}^{{(2)}}\left( {t,\tau } \right)$ = = $\frac{{\left\langle {\hat {c}_{i}^{ + }\left( t \right){{{\hat {c}}}_{i}}\left( t \right)\hat {c}_{i}^{ + }\left( {t + \tau } \right){{{\hat {c}}}_{i}}\left( {t + \tau } \right)} \right\rangle }}{{\left\langle {\hat {c}_{i}^{ + }\left( t \right){{{\hat {c}}}_{i}}\left( t \right)} \right\rangle \left\langle {\hat {c}_{i}^{ + }\left( {t + \tau } \right){{{\hat {c}}}_{i}}\left( {t + \tau } \right)} \right\rangle }} - 1.$

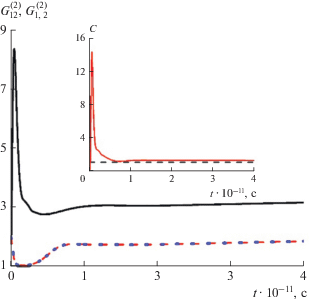
Принципиальным результатом для рассмотренной нелинейной модели с одной КТ и двумя НЧ является возникновение сильных неклассических черт у фотонов, формируемых при распаде биэкситонов. В частности, численное моделирование системы на билинейные комбинации операторов плазмонов и экситонов позволяет получить зависимость фотонной кросс-корреляционной функции $G_{{12}}^{{(2)}}$ от времени (рис. 3). При выборе параметров, используемых на рис. 2, кривые изменения $G_{{12}}^{{(2)}}$ во времени демонстрируют выход на стационарный уровень. Величина параметра $G_{{12}}^{{(2)}}$ в таких стационарных условиях составит приблизительно 3.14, что демонстрирует группировку фотонов между модами. Кроме того, наблюдается нарушение соотношения Коши–Шварца: параметр С приобретает значение 1.2 для стационарного режима генерации плазмонов, а в точке максимума (вставка на рис. 3) даже достигает значения 14.24. При этом начальные корреляции между плазмонами (а также фотонами) соседних мод полностью отсутствуют. Таким образом, представленная на рис. 1 схема трехчастичного спазера может быть использована в качестве источника перепутанных состояний электромагнитного поля, реализованного в наномасштабе.

Достаточно простым способом влияния на квантовые свойства генерируемых в спазере фотонов является изменение величины магнитного поля. Так, с увеличением индукции поля ${{B}_{m}}$ растет зеемановское расщепление уровней КТ, меняются параметры ${{\delta }_{{1,2}}},$ и в условиях сохраняющегося устойчивого режима корреляционные функции (рис. 3) выходят на новый уровень значений. Такая перестройка может осуществляться достаточно плавно, так как вклад слагаемых с ${{B}_{m}}$ оказывается существенно меньшим, чем $\bar {\omega } - {{\omega }_{X}}$ в составе частотных отстроек ${{\delta }_{{1,2}}}.$

В свою очередь потеря устойчивости режимов генерации фотонов в рассмотренной схеме обусловлена в основном геометрической точностью и химической чистотой отдельных компонент – НЧ и КТ, а также их взаиморасположения в составе спазера. Вместе с тем необходимо учитывать влияние магнитного поля на квантовое состояние пары распадающихся экситонов в КТ, которое может проявлять зависимость от формы частиц [20]. Другим важным вопросом является проблема временной стабильности отдельных КТ в процессе установления стационарного режима работы спазера, аналогично проблеме мерцания излучающих КТ [21]. Однако решение данного круга проблем находится в иной плоскости, в разделе современных практических нанотехнологий. В частности, отдельного внимания требует изучение температурных зависимостей обсуждаемых эффектов [22] и сложной внутренней динамики на примере реальных физических систем [23].

ЗАКЛЮЧЕНИЕ

Осуществлен последовательный вывод гамильтониана нелинейного плазмон-экситонного взаимодействия в трехчастичной спазерной системе, описывающего двухквантовый процесс распада биэкситонных состояний полупроводниковой квантовой точки с одновременным формированием пары поверхностных плазмонов, локализующихся на металлических наночастицах, связанных ближним полем с квантовой точкой. Коэффициенты при соответствующих слагаемых гамильтониана являются функциями управляющих параметров системы. Показана возможность формирования перепутанных фотонов в трехчастичном спазере за счет нелинейных процессов с биэкситонными состояниями в КТ. Практический выход работы связан с использованием эффекта для создания высокоэффективных ярких источников неклассических фотонов.