Известия РАН. Серия физическая, 2020, T. 84, № 3, стр. 310-316
Микроволны для эффективного манипулирования ядерными спинами в системах NV-13C в алмазе
А. П. Низовцев 1, 2, *, С. Я. Килин 1
1 Институт физики имени Б.И. Степанова Национальной академии наук Беларуси
Минск, Беларусь
2 Федеральное государственное автономное образовательное учреждение высшего образования
“Национальный исследовательский ядерный университет “МИФИ”
Москва, Россия
* E-mail: apniz@ifanbel.bas-net.by
Поступила в редакцию 20.09.2019
После доработки 15.11.2019
Принята к публикации 27.11.2019
Аннотация
Изучена нестационарная динамика связанных сверхтонким взаимодействием электронно-ядерных cпиновых cиcтем 14NV–13C в алмазе под действием микроволнового излучения. Выяснены и интерпретированы оптимальные условия эффективного когерентного манипулирования микроволнами состоянием ядерного спина 13С в таких системах.
ВВЕДЕНИЕ
Возможность создавать, контролировать и считывать когерентные состояния многоспиновых систем в твердых телах принципиально важна для квантовой обработки информации, магнитометрии, метрологии и т.п. Для этих целей особенно перспективными являются системы взаимодействующих электронных и ядерных спинов, в которых электроны играют роль “быстрых” кубит и могут использоваться в качестве интерфейсов с “летающими” кубитами – фотонами, а ядерные спины могут хранить квантовую информацию в течение долгого времени благодаря их исключительно высокой изоляции от окружения.
Наиболее известным представителем таких систем является центр окраски “азот–вакансия” (NV-центр) в алмазе (см., например, [1, 2]), электронный спин S = 1 которого в основном электронном состоянии сверхтонко взаимодействует с ядерным спином I(N) = 1 атома 14N, принадлежащего данному NV-центру, и, потенциально, – с соседними ядерными спинами I(C) = 1/2 изотопических атомов 13C, распределенных случайно в решетке алмаза и замещающих безспиновые атомы 12C с вероятностью 1.1%. Электронные спины NV-центров обладают большим временем когерентности при комнатной температуре и для осуществления однокубитных логических операций их состоянием можно когерентно манипулировать на временах ~ наносекунд с помощью импульсных микроволн. Сверхтонкие взаимодействия (СТВ) электронного спина центра с ядерными спинами 13C обеспечивают возможность исполнения многокубитных операций, при реализации которых манипулирование состояниями ядерного спина атома 13С осуществляется обычно с помощью импульсного радиочастотного излучения, имеющего уже микросекундную длительность. В настоящее время можно считать хорошо отработанными методы инициализации, когерентного манипулирования и измерения с высокой точностью частот переходов и состояний систем 14NV–13C (в том числе содержащих достаточно удаленные от NV-центра ядерные спины) с целью их использования в качестве квантовых регистров и квантовой памяти, а также для реализации квантовой коррекции ошибок, квантовой метрологии и т.п. Для всех этих приложений необходимо детально знать характеристики СТВ для систем NV–13C и понимать их динамику под влиянием внешних воздействий.
Недавно систематические расчеты матриц ${{A}_{{KL}}},$ описывающих СТВ электронного спина NV-центра с различным образом расположенными ядерными спинами 13С, были выполнены в [3, 4], где методом функционала плотности моделировались кластеры алмаза C291[NV]–H172 и C510[NV]–H252, содержащие NV-центр. Используя полученные расчетные данные в спин-гамильтонианах, описывающих системы NV–13C, можно найти различные экспериментально наблюдаемые характеристики, а также предсказать оптимальные условия получения желаемых экспериментальных результатов. Для данной работы важным является то, что, согласно сделанным в [4] предсказаниям, для большинства систем NV–13C анизотропная составляющая СТВ, описываемая недиагональными элементами матрицы ${{A}_{{KL}}},$ не является малой. Как показано в [5–7], это позволяет использовать метод двойного резонанса Хартмана–Хана [8] для когерентного манипулирования состояниями ядерных спинов 13С в системах NV–13C, “одетых” микроволновым излучением (МВИ). Здесь, используя расчетные данные работы [4] о матрицах СТВ для различных спиновых систем NV–13C, мы изучаем их нестационарную динамику под действием МВИ и находим его характеристики, обеспечивающие эффективное, с вероятностью порядка 1, манипулирование состоянием ядерного спина 13С в таких системах.
СПИН-ГАМИЛЬТОНИАН И МОДЕЛЬ СИСТЕМЫ 14NV–13C
Для моделирования спиновой системы 14NV–13C, состоящей из электронного спина $S$ = 1 NV-центра, взаимодействующего с ним ядерного спина I(N) = 1 атома 14N, входящего в состав центра, и ядерного спина $I_{i}^{{{\text{(C)}}}}$ = 1/2 атома 13C, расположенного в некотором узле решетки алмаза вблизи NV-центра, используем стандартный спин-гамильтониан $H$ такой спиновой системы [1, 4]
(1)
$\begin{gathered} H = H_{0}^{{{\text{(NV)}}}} + \vec {S} \cdot {{A}^{{{\text{(С)}}}}} \cdot {{{\vec {I}}}^{{({\text{С}})}}} + \\ + \,\,\gamma _{e}^{{{\text{(NV)}}}}\vec {S} \cdot \vec {B} - \gamma _{n}^{{({\text{N}})}}{{{\vec {I}}}^{{({\text{N}})}}} \cdot \vec {B} - \gamma _{n}^{{({\text{С}})}}{{{\vec {I}}}^{{({\text{С}})}}} \cdot \vec {B}. \\ \end{gathered} $Здесь первый член
(2)
$\begin{gathered} H_{0}^{{{\text{(NV)}}}} = D\left[ {S_{Z}^{2} - {{S(S + 1)} \mathord{\left/ {\vphantom {{S(S + 1)} 3}} \right. \kern-0em} 3}} \right] + \vec {S} \cdot {{A}^{{({\text{N}})}}} \cdot {{{\vec {I}}}^{{({\text{N}})}}} + \\ + \,\,Q\left[ {{{{(I_{Z}^{{({\text{N}})}})}}^{2}} - {{{{I}^{{({\text{N}})}}}({{I}^{{({\text{N}})}}} + 1)} \mathord{\left/ {\vphantom {{{{I}^{{({\text{N}})}}}({{I}^{{({\text{N}})}}} + 1)} 3}} \right. \kern-0em} 3}} \right] \\ \end{gathered} $учитывает расщепление при нулевом магнитном поле подуровней ${{m}_{S}}$ = 0 и ${{m}_{S}}$ = ±1 электронного спина центра (D = 2872 МГц), “внутреннее” СТВ в центре (${{A}^{{{\text{(N)}}}}}$есть тензор СТВ между спинами $\vec {S}$ и ${{\vec {I}}^{{{\text{(N)}}}}},$ являющийся диагональным с элементами $A_{{XX}}^{{{\text{(N)}}}} = A_{{YY}}^{{{\text{(N)}}}}$ = –2.14 МГц и $A_{{ZZ}}^{{{\text{(N)}}}}$ = –2.70 МГц в системе главных осей (СГО) NV-центра, в которой ось Z совпадает с осью симметрии С3V центра) и квадрупольный момент ядра 14N Q = –5.01 МГц. Второй член в (1) учитывает СТВ между спинами $\vec {S}$ и ${{\vec {I}}^{{{\text{(C)}}}}},$ описываемое матрицей A(C), которая в общем случае не является диагональной в СГО NV- центра. Последние три члена в (1) описывают взаимодействия всех трех спинов $\vec {S}$, ${{\vec {I}}^{{{\text{(N)}}}}}$и ${{\vec {I}}^{{{\text{(C)}}}}}$ с внешним магнитным полем $\vec {B}$ (здесь $\gamma _{e}^{{{\text{(NV)}}}}$ = = 2.803 МГц/гаусс, $\gamma _{n}^{{{\text{(N)}}}}$ = 0.3078 кГц/гаусс и $\gamma _{n}^{{(C)}}$ = = 1.0708 кГц/гаусс – гиромагнитные отношения для электронного спина NV-центра и ядерных спинов 14N и 13C соответственно.
Диагонализация гамильтониана (1) дает (2S + + 1)(2I(N) + 1)(2I(C) + 1) = 18 энергий ${{E}_{\alpha }}$ трехспиновой системы и коэффициенты $c_{{\alpha }}^{{{{m}_{S}},m_{I}^{{[N]}},m_{I}^{{[C]}}}}$ в спиновых волновых функциях $\left| {{{\Psi }_{{\alpha }}}} \right\rangle $ при их представлении в виде разложения
(3)
$\begin{gathered} \left| {{{\Psi }_{{\alpha }}}} \right\rangle = \\ = \sum\limits_{{{m}_{S}} = - S}^S {\sum\limits_{m_{I}^{{{\text{(N)}}}} = - {{I}^{{{\text{(N)}}}}}}^{{{I}^{{{\text{(N)}}}}}} {\sum\limits_{m_{I}^{{({\text{C}})}} = - {{I}^{{{\text{(C)}}}}}}^{{{I}^{{(C)}}}} {c_{{\alpha }}^{{{{m}_{S}},m_{I}^{{{\text{[N]}}}},m_{I}^{{{\text{[C]}}}}}}\left| {{{m}_{S}},m_{I}^{{{\text{[N]}}}},m_{I}^{{{\text{[C]}}}}} \right\rangle } } } \\ \end{gathered} $по базису, образованному спиновыми состояниями $\left| {{{m}_{S}},m_{I}^{{{\text{[N]}}}},m_{I}^{{{\text{[C]}}}}} \right\rangle ,$ соответствующими определенным магнитным квантовым числам ${{m}_{S}}$ и $m_{I}^{{{\text{[N]}}}},$ $m_{I}^{{[{\text{C}}]}}$ проекций электронного и ядерных спинов на ось Z.
Внешнее магнитное поле $\vec {B}$ снимает вырождение уровней с проекциями электронного спина ${{m}_{S}}$ = ±1. Поскольку проекция ядерного спина атома азота 14N может быть фиксирована [1, 2], для простоты будем далее рассматривать случай $m_{I}^{{{\text{[N]}}}}$ = +1. Предположим также, что на систему действует МВИ, квазирезонансное переходам между подуровнями NV-центра с проекциями электронного спина ${{m}_{S}}$ = 0 и mS = –1. В таком случае в качестве модели системы NV–13C вместо 16-уровневой системы можно рассматривать 4‑уровневую квантовую систему, включающую в себя только состояния с ${{m}_{S}}$ = 0, –1 и $m_{I}^{{{\text{[N]}}}}$ = +1.
Вследствие условия $\left| {{{A}_{{KL}}}} \right| \ll D$ для большинства систем NV–13C можно использовать секулярное приближение, в котором в гамильтониане (1) оставляются только члены с SZ. В этом приближении энергии модельной 4-уровневой системы 14NV–13C в магнитном поле $\vec {B}$ || OZ задаются выражениями
(4)
$\begin{gathered} {{E}_{{4,3}}} \simeq D{\text{/}}3 - \gamma _{e}^{{{\text{(NV)}}}}B \pm \Delta {\text{/}}2,\,\,\,\,({{m}_{S}} = - 1), \\ {{E}_{{1,2}}} \simeq - 2D{\text{/}}3 \pm \gamma _{n}^{{{\text{(C)}}}}B{\text{/}}2,\,\,\,\,({{m}_{S}} = 0), \\ \end{gathered} $(5)
$\begin{gathered} \left| {{{\Psi }_{1}}} \right\rangle = \left| {0 \uparrow \nearrow } \right\rangle ,\,\,\,\,\left| {{{\Psi }_{2}}} \right\rangle = \left| {0 \uparrow \swarrow } \right\rangle , \\ \left| {{{\Psi }_{3}}} \right\rangle = \alpha \left| { \Downarrow \uparrow \nearrow } \right\rangle + \beta \exp (i\varphi )\left| { \Downarrow \uparrow \swarrow } \right\rangle , \\ \left| {{{\Psi }_{4}}} \right\rangle = - \beta \left| { \Downarrow \uparrow \nearrow } \right\rangle + \alpha \exp (i\varphi )\left| { \Downarrow \uparrow \swarrow } \right\rangle , \\ \end{gathered} $Из (5) с учетом правил отбора $\Delta {{m}_{S}} = \pm 1$ для ЭПР-переходов в системе NV–13C следует, что в типичном случае $\left( {{{A}_{{nd}}} \ne 0} \right)$ МВИ может инициировать переходы из состояний 1 и 2 на оба верхних состояния 3 и 4.
Вероятности таких переходов зависят от значений параметров $\alpha $ и $\beta .$ Какие из переходов являются “сильными” или “слабыми” (т.е. имеют большую или малую
вероятность), зависит не только от абсолютных значений элементов ${{A}_{{YZ}}},{{A}_{{XZ}}},{{A}_{{ZZ}}}$ и магнитного поля В, но и от знака величины ${{A}_{{ZZ}}} + {{\gamma }^{{{\text{(C)}}}}}B.$ В слабых полях ${{\gamma }^{{{\text{(C)}}}}}B \ll \left| {{{A}_{{ZZ}}}} \right|$ и в типичной ситуации, когда $\left| {{{A}_{{ZZ}}}} \right| > {{A}_{{nd}}},$ угол θ близок к $\pi $ при ${{A}_{{ZZ}}}$ < 0 и к нулю при ${{A}_{{ZZ}}}$ > 0, так что  ~ 1,
~ 1,  ~ 0 в первом случае, а во втором случае будем иметь
~ 0 в первом случае, а во втором случае будем иметь  ~ 0,
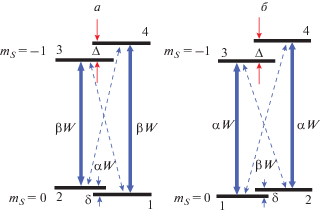
~ 0,  ~ 1. В результате в слабых полях и при ${{A}_{{ZZ}}}$ < 0 “сильными” будут переходы 1–4 и 2–3 $\left( {\beta \gg \alpha } \right),$ а при ${{A}_{{ZZ}}}$ > 0 – переходы 1–3 и 2–4 $\left( {\alpha \gg \beta } \right).$ Соответственно, имеется два типа модельных систем NV–13C, представленных на рис. 1а и 1б.
~ 1. В результате в слабых полях и при ${{A}_{{ZZ}}}$ < 0 “сильными” будут переходы 1–4 и 2–3 $\left( {\beta \gg \alpha } \right),$ а при ${{A}_{{ZZ}}}$ > 0 – переходы 1–3 и 2–4 $\left( {\alpha \gg \beta } \right).$ Соответственно, имеется два типа модельных систем NV–13C, представленных на рис. 1а и 1б.
ДИНАМИКА СИСТЕМ NV–13C ПОД ДЕЙСТВИЕМ МВИ
Нестационарная эволюция модельной 4-уровневой квантовой системы в поле МВИ с частотой ω, близкой к частотам переходов 1, 2–3, 4, описывается уравнением Шредингера для волновой функции $\left| {\Psi (t)} \right\rangle $ = $\sum\nolimits_k {{{a}_{k}}} \left| {{{\Psi }_{k}}} \right\rangle \exp ( - i{{E}_{k}}t)$ (k = 1–4), в котором взаимодействие с МВИ будем описывать оператором $W(t) = {{W}^{ + }}\exp ( - i\omega t)$ + ${{W}^{ - }}\exp (i\omega t).$ В соответствии с правилами отбора матричные элементы $W = \left\langle { \Downarrow \uparrow \nearrow } \right|{{W}^{ \pm }}\left| {0 \uparrow \nearrow } \right\rangle $ = $\left\langle { \Downarrow \uparrow \swarrow } \right|{{W}^{ \pm }}\left| {0 \uparrow \swarrow } \right\rangle $ операторов W± отличны от нуля для состояний с разными проекциями электронного спина и одинаковыми проекциями ядерного спина. С учетом (5) это означает, что матричные элементы переходов между состояниями 1, 2 и 3, 4 модельной системы будут равны αW или βW, причем, как уже отмечалось выше, величины коэффициентов α и β зависят от знака ${{A}_{{ZZ}}}.$ Учитывая сказанное, вводя расстройку резонанса $\varepsilon = {{\omega }_{{4,1}}} - \omega $ и выражая через нее расстройки для остальных переходов в рассматриваемых модельных системах, несложно построить систему уравнений с осциллирующими коэффициентами для амплитуд вероятностей ak(t), которая имеет одинаковый вид для обеих спиновых систем, представленных на рис. 1а и 1б. Делая в ней замены переменных ${{\bar {a}}_{4}} = {{a}_{4}}\exp ( - i(\varepsilon - \delta )t),$ ${{\bar {a}}_{3}} = {{a}_{3}}exp( - i(\varepsilon - \Delta - \delta )t),$ ${{\bar {a}}_{2}} = {{a}_{2}}exp( - i\varphi )$ и ${{\bar {a}}_{1}} = {{a}_{1}}\exp (i\delta t),$ для компонент ${{\bar {a}}_{i}}$ можно получить уравнение с постоянными коэффициентами, которое, вводя вектор $\bar {R}$ = = ${{({{\bar {a}}_{4}},{{\bar {a}}_{3}},{{\bar {a}}_{2}},{{\bar {a}}_{1}})}^{T}},$ можно записать в матричном виде
(6)
$\begin{gathered} {{{\dot {\bar {R}}}}^{t}} = i\bar {M}{{{\bar {R}}}^{t}}, \\ \bar {M} = \left( {\begin{array}{*{20}{c}} { - \varepsilon + \delta }&0&{ - \alpha W}&{\beta W} \\ 0&{ - \varepsilon + \Delta + \delta }&{ - \beta W}&{ - \alpha W} \\ { - \alpha W}&{ - \beta W}&0&0 \\ {\beta W}&{ - \alpha W}&0&\delta \end{array}} \right) \\ \end{gathered} $и искать его нестационарное решение в виде ${{\bar {R}}^{t}} = \exp (i\bar {M}t){{\bar {R}}_{0}},$ где ${{\bar {R}}_{0}}$ – вектор, описывающий начальное состояние спиновой системы. Поскольку оптическая накачка NV-центра переводит его с вероятностью ~1 в состояние с проекцией электронного спина mS = 0, будем в качестве исходного брать состояние 1 = $\left| {0 \uparrow \nearrow } \right\rangle .$ Зависящие от времени вероятности найти в момент времени t систему NV–13C в состояниях 4-1 определяются решениями уравнения (6): $P_{4}^{t} = {{\left| {{{{\overline R }}^{t}}(1)} \right|}^{2}},$ $P_{3}^{t} = {{\left| {{{{\bar {R}}}^{t}}(2)} \right|}^{2}},$ $P_{2}^{t} = {{\left| {{{{\bar {R}}}^{t}}(3)} \right|}^{2}},$ $P_{1}^{t} = {{\left| {{{{\bar {R}}}^{t}}(4)} \right|}^{2}},$ где ${{\bar {R}}^{t}}(i)$ – компоненты вектора ${{\bar {R}}^{t}}.$ Как показано ниже, для двух различных спиновых систем, представленных на рис. 1а и 1б, уравнение (6), имея одинаковый вид, дает существенно разные результаты вследствие различного соотношения для них параметров α и β.
Решение уравнений (6) и анализ нестационарного поведения соответствующих спиновых систем будем проводить численно, а для интерпретации полученных численных результатов будем использовать аналитические выражения, полученные в рамках секулярного приближения. В частности, оно хорошо работает для систем NV–13C, в которые входит ядерный спин 13C, являющийся вторым и третьим соседом вакансии. Кроме того, согласно базе данных, полученной в работе [4], для всех вторых соседей ${{A}_{{ZZ}}}$ < 0, а для всех третьих соседей ${{A}_{{ZZ}}}$ > 0, так что они как раз являются представителями систем, изображенных на рис. 1а и 1б соответственно. Здесь мы приведем результаты численного анализа динамики под действием МВИ, выполненного для двух конкретных систем: в первом случае (рис. 1а) выберем систему 14NV–13C234, а во втором (рис. 1б) – систему 14NV–13C159, где нижний индекс у 13С указывает номер его позиции в базе данных, полученной в [4]. Рассчитанные в [4] матрицы ${{A}_{{KL}}}$ для систем 14NV–13C234 и 14NV–13C159 имели вид (в МГц):
(7)
$\begin{gathered} {{A}^{{{{С}_{{159}}}}}} = \left( {\begin{array}{*{20}{c}} {10.6987 }&{1.1499}&{0.5282} \\ {1.1499}&{13.2551}&{1.3779} \\ {0.5282}&{1.3779}&{11.1276} \end{array}} \right), \\ {{A}^{{{{С}_{{234}}}}}} = \left( {\begin{array}{*{20}{c}} { - 3.8682 }&{0.8184}&{ - 0.8851} \\ {0.8184}&{ - 6.0693}&{ - 0.2959} \\ { - 0.8851}&{ - 0.2959}&{ - 6.3569} \end{array}} \right), \\ \end{gathered} $В магнитном поле В = 200 гаусс (B||OZ) состояния системы 14NV–13C234, рассчитанные численной диагонализацией спин-гамильтониана (1), имели энергии, соответствующие частотам переходов ω21 = 0.2126 МГц, ω31 = 2308.5106 МГц и ω41 = = 2314.7285 МГц (ω43= 6.2179 МГц), которые хорошо аппроксимируются аналитическими выражениями (4), где для данной спиновой системы Δ = 6.2134 МГц, $\delta $ = 0.2141 МГц. Соответственно, собственные функции для нее имели вид (2) при $\alpha $ = 0.0762, $\beta $ = 0.9972, $\varphi $ = –2.8189 радиан. Аналогично, для системы 14NV–13C159 численная диагонализация гамильтониана (1) дает частоты переходов ω21 = 0.2042 МГц, ω31= 2305.8626 МГц и ω41 = 2317.2702 МГц (ω43 = 11.4076 МГц), что также хорошо соответствует аналитическим результатам: $\Delta $ = 11.4374 МГц и $\delta $ = 0.2142 МГц. Для собственных функций (4) в данном случае параметры имели значения: $\alpha $ = 0.9979, $\beta $ = 0.0649, $\varphi $ = = 1.2047 радиан.
Анализ нестационарной эволюции заселенности $P_{2}^{t}$ состояния 2 = $\left| {0 \uparrow \swarrow } \right\rangle $ для систем 14NV–13C234 и 14NV–13C159 при начальном их состоянии 1 = $\left| {0 \uparrow \nearrow } \right\rangle $, выполненный численным решением уравнения (6) при определенных значениях расстройки ε и мощности W МВИ, показал, что максимально достижимая заселенность $P_{2}^{t}$ существенно зависит от выбранных значений ε и W и в некоторых случаях она может быть близка к 1. Результаты таких расчетов показаны на рис. 2 в виде трехмерных графиков и в виде их проекции на плоскость ε, W. Из этих рисунков видно, что максимально достижимая вероятность заселения состояния 2 из состояния 1 под действием МВИ реализуется лишь в узкой области взаимосвязанных параметров ε, W. В частности, для системы 14NV–13C234 это имеет место уже при сравнительно малых мощностях МВИ и остается таковым при увеличении мощности МВИ при соответствующем линейном увеличении оптимальной расстройки резонанса. В случае системы 14NV–13C159 заселенность Р2 максимальна лишь вблизи значений параметра W, меньших некоторого критического значения Wкрит (для системы 14NV–13C159Wкрит ~ 0.7647 МГц), при превышении которого вероятность переворота спина 13С быстро убывает. Максимально достижимая заселенность состояния 2 составляет 0.9411 и 0.966 для систем 14NV–13C234 и 14NV–13C159 соответственно.
Рис. 2.
Трехмерные графики зависимости максимально достижимой заселенности состояния 2 из состояния 1 от расстройки резонанса ε = ω41 – ω и мощности W микроволн, полученные численным решением уравнения (6) для систем 14NV–13C234 (а) и 14NV–13C159 (б) и их проекции на плоскость ε, W (рис. в и г).

На рис. 3а и 3б представлены примеры нестационарного поведения заселенностей этих систем, полученные численным решением уравнения (6) при указанных в подписи к рисунку оптимальных значениях параметров W и ε. Из рисунков видно, что в моменты времени ~17 и 19 мкс имеет место почти полная инверсия перехода 1–2, т.е. МВИ такой длительности реализуют с вероятностью ~1 переворот ядерного спина 13С из состояния 1 в состояние 2.
Рис. 3.
Нестационарная эволюция заселенностей состояний спиновых систем 14NV–13C234 (а) и 14NV–13C159 (б) при воздействии на них МВИ с оптимальными характеристиками, взятыми с графиков рис. 2. В первом случае взяты значения W = 5 МГц, ε4,1 = 29.4318 МГц, а во втором – W = 0.76 МГц, ε4,2 = 6.2415 МГц. Кривые 1–4 представляют заселенности состояний 1–4 соответственно.

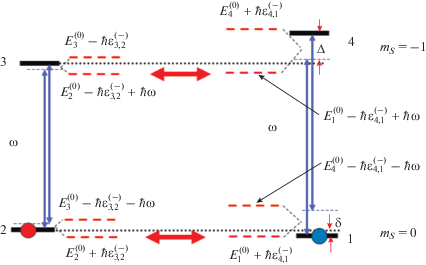
Для интерпретации полученных численно оптимальных значений параметров МВИ рассмотрим представленные на рис. 2 спиновые системы NV–13C как состоящие из двух связанных СТВ “одетых” полем МВ-излучения двухуровневых систем (ДУС), включающих состояния 1–4 и 2–3 в случае системы 14NV–13C234 и состояния 1–3, 2–4 – в случае системы 14NV–13C159. .При полуклассическом описании взаимодействия ДУС $b - a$ с невозмущенными энергиями $E_{b}^{{(0)}}$ и $E_{a}^{{(0)}}$ ($E_{b}^{{(0)}} > E_{a}^{{(0)}}$) и собственными функциями $\Psi _{b}^{{(0)}}$ и $\Psi _{a}^{{(0)}}$ с полем излучения частоты $\omega \sim {{\omega }_{{ba}}}$ квазиэнергетические состояния (КЭС) такой ДУС в резонансном приближении имеют вид (см., например, [9])
(8а)
${{\Phi }_{a}} = {{e}^{{{{ - i\left( {E_{a}^{{(0)}} + \hbar {\varepsilon }_{{b,a}}^{{( - )}}} \right)t} \mathord{\left/ {\vphantom {{ - i\left( {E_{a}^{{(0)}} + \hbar {\varepsilon }_{{b,a}}^{{( - )}}} \right)t} \hbar }} \right. \kern-0em} \hbar }}}}\sqrt {\frac{{\varepsilon _{{b,a}}^{{( + )}}}}{{{{\Omega }_{{b,a}}}}}} \left( {\Psi _{a}^{{(0)}} - \frac{{W_{{b,a}}^{ + }}}{{\varepsilon _{{b,a}}^{{( + )}}}}\Psi _{b}^{{(0)}}{{e}^{{ - i{\omega }t}}}} \right),$Рис. 4.
Иллюстрация совпадения КЭ уровней правой и левой ДУС рис. 1а в случае $\omega < {{\omega }_{{3,2}}},$ ${{\omega }_{{4,1}}},$ когда расстройки МВИ для обеих ДУС положительны.
Анализ КЭ-уровней ДУС 4–1 и 3–2, выполненный на основе выражений (8), показал, что при заданной мощности микроволн во всех случаях совпадение энергий КЭС этих ДУС имеет место при значениях расстройки ${{\varepsilon }_{{4,1}}},$ связанных с W следующим простым выражением:
(9)
$\varepsilon _{{4,1}}^{{опт[ \pm ]}} = \frac{{\Delta + \delta }}{2} \pm \frac{{\Delta - \delta }}{2}\sqrt {1 + \frac{{4{{\beta }^{2}}{{W}^{2}}}}{{\Delta \delta }}} .$В случае слабого МВИ $W \to 0$ оптимальные значения расстройки (9) приближенно равны $\varepsilon _{{4,1}}^{{опт[ + ]}} \approx \Delta ,$ $\varepsilon _{{4,1}}^{{опт[ - ]}} \approx \delta ,$ а при увеличении мощности МВИ они зависят от W линейно. Аналогичный анализ, выполненный для системы, представленной на рис. 1б, показал, что для нее совпадение КЭ-уровней “одетых” микроволнами ДУС 1-3 и 2-4 имеет место при значениях параметров, удовлетворяющих соотношениям
(10)
$\varepsilon _{{4,2}}^{{^{{опт[ \pm ]}}}} = \frac{{\Delta - \delta }}{2} \pm \frac{{\Delta + \delta }}{2}\sqrt {1 - \frac{{4{{\alpha }^{2}}{{W}^{2}}}}{{\Delta \delta }}} ,$принципиальное отличие которых от (9) состоит в наличии знака “минус” под корнем, означающего, что в данном случае пересечение КЭ-уровней возможно только при мощностях W микроволн, не превышающих критическое значение Wкрит = $\sqrt {\Delta \delta {\text{/}}4{{\alpha }^{2}}} .$ Для системы 14NV–13C159формула (10) дает значение Wкрит = 0.7747 МГц. Отметим здесь, что, в отличие от (9), условие (10) записано для расстройки резонанса ${{\varepsilon }_{{4,2}}}.$ Нетрудно проверить, что для обеих систем графики зависимостей оптимальных расстроек $\varepsilon _{{4,1}}^{{( \pm )}}$ от частоты Раби $\beta W,$ рассчитанные по формулам (9), (10), практически полностью совпадают с показанными рис. 2в и 2г численными результатами для заселенности ${{P}_{2}}(\max )\sim 1$ состояния 2.
Таким образом, проведенные численные расчеты и их анализ на основе представления об “одетых” системах NV–13C позволил получить простые соотношения для взаимосвязанных характеристик МВИ, обеспечивающих эффективное манипулирование ядерным спином 13С. Используя базу данных работы [4], аналогичные расчеты могут быть выполнены и для других систем NV–13C, в том числе – исследованных экспериментально в [5].
Работа выполнена в рамках республиканской ГПНИ “Конвергенция-2020” и сотрудничества с НИЯУ МИФИ.
Список литературы
Doherty M.W., Manson N.B., Delaney P. et al. // Phys. Rep. 2013. V. 528. P. 1.
Dobrovitski V.V., Fuchs G.D., Falk A.L. et al. // Ann. Rev. Cond. Matt. Phys. 2013. V. 4. P. 23.
Nizovtsev A.P., Kilin S.Ya., Pushkarchuk A.L. et al. // New J. Phys. 2014. V. 16. Art. № 083014.
Nizovtsev A.P., Kilin S.Ya., Pushkarchuk A.L. et al. // New J. Phys. 2018. V. 20. Art. № 023022.
London P., Scheuer J., Cai J.-M. et al. // Phys. Rev. Lett. 2013. V. 111. Art. № 067601.
Hodges J.S., Yang J.C., Ramanathan C. et al. // Phys. Rev. A. 2018. V. 78. Art. № 010303(R).
Aiello C.D., Cappellaro P. // Phys. Rev. A. 2015. V. 91. Art. № 042340.
Hartmann S.R., Hahn E.L. // Phys. Rev. 1962. V. 128. P. 2042.
Тер-Микаелян М.Л. // Препринт ИФИ-74-11. Аштарак, 1974.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая