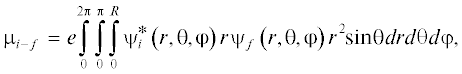Известия РАН. Серия физическая, 2020, T. 84, № 3, стр. 418-424
Цифровое проектирование и оптимизация параметров плазмонных схем
А. В. Шестериков 1, А. Ю. Лексин 1, Т. В. Прохорова 1, Н. М. Воронова 1, А. В. Прохоров 1, *
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых”
Владимир, Россия
* E-mail: avprokhorov33@mail.ru
Поступила в редакцию 20.09.2019
После доработки 15.11.2019
Принята к публикации 27.11.2019
Аннотация
Рассмотрены вопросы применения численных методов и алгоритмов для проектирования плазмонных схем на основе двумерных материалов и полупроводниковых квантовых точек. Описываются математические подходы как основа для системы автоматизированного расчета параметров полупроводниковых квантовых точек сферической формы, а также особенности применения метода конечных разностей во временной области для полного полевого моделирования вблизи поверхности наноструктурированного графена.
ВВЕДЕНИЕ
Вопросы создания и использования программного обеспечения для расчета гибридных схем резонансного взаимодействия между отдельными эмиттерами и электромагнитным полем является слабым местом практически всех доступных коммерческих программ. В контексте рассматриваемых задач гибридными являются такие схемы взаимодействия, в которых квантовый эмиттер (атом, молекула, квантовая точка (КТ), квантовый провод (КП)) испытывает одновременное воздействие как свободного электромагнитного поля, так и локализованных электромагнитных волн. Такие волны – поверхностные плазмон-поляритоны (ППП) – формируются в волноводных интерфейсах на границе материалов с резким контрастом диэлектрической проницаемости (металл/диэлектрик); их преимущество перед свободно распространяющимися волнами заключается в возможности пространственной локализации на масштабах порядка нескольких нанометров, существенно меньше длины волны света. Одновременно с этим характерные частоты таких возбуждений могут соответствовать терагерцевому, инфракрасному и даже оптическому диапазонам, что позволяет добиться беспрецедентных скоростей отклика и нанометровых масштабов устройств на их основе.
В настоящей работе рассматриваются вопросы разработки и реализации математических моделей для проектирования плазмонных схем на основе полупроводниковых квантовых точек и наноструктурированного графена. Для этого, была создана база данных характеристик КТ на основе соединений A3B5 и A2B6, вмещающая в себя информацию о параметрах энергий потолка валентной зоны, дна зоны проводимости, ширины запрещенной зоны и т.д. Разработанные математические методы позволили производить автоматизированный расчет энергетической структуры уровней, частот и дипольных моментов, скоростей релаксации и др.
На следующем этапе были проведены работы по реализации метода конечных разностей во временной области для моделирования распространения ППП в плазмонных волноводах на основе проводящих структур как перспективных сред для реализации межузловых соединений в плазмонных схемах. Составлена математическая модель по реализации метода конечных разностей во временной области (FDTD) для моделирования плазмон-поляритонных мод в графеновых двумерных структурах. Проведено тестирование на примере сравнения результатов расчета с результатами известных работ по моделированию распространения ППП в графеновых схемах [1, 2]. Получено полное согласие результатов работы авторских методов как с коммерческими программами, так и с практическими работами зарубежных авторов на оригинальном коде.
МОДЕЛЬ РАСЧЕТА ЗАВИСИМОСТЕЙ ПОЛОЖЕНИЯ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ ДЛЯ ПОЛУПРОВОДНИКОВЫХ КТ ЗАДАННОГО РАЗМЕРА
Для расчета размерных зависимостей ограниченного числа энергетических уровней дырки в валентной зоне КТ может быть использовано оценочное соотношение [3–6]
(1)
$\begin{gathered} {{E}_{{nl}}} = {{E}_{V}}e - \frac{{{{\hbar }^{2}}\chi _{{nl}}^{2}}}{{2{{m}_{h}}{{a}^{2}}}}~,\,\,n = 1,\,\,2,\,\,3,\,\, \ldots ,\,{{n}_{{max}}}; \\ l = 0,\,\,1,\,\, \ldots ,\,\,{{l}_{{max}}}, \\ \end{gathered} $(2)
$\begin{gathered} {{E}_{{n{\kern 1pt} 'l{\kern 1pt} '}}} = {{E}_{c}}e + \frac{{{{\hbar }^{2}}\chi _{{n{\kern 1pt} 'l{\kern 1pt} '}}^{2}}}{{2{{m}_{e}}{{a}^{2}}}},\,\,\,n{\kern 1pt} ' = 1,2, \ldots n_{{max}}^{'}; \\ l{\kern 1pt} ' = 0,1,2, \ldots l_{{max}}^{'}, \\ \end{gathered} $(3)
${{\omega }_{{mn}}} = \frac{1}{\hbar }\left( {\frac{{{{\hbar }^{2}}}}{{2{{m}_{h}}{{a}^{2}}}}\left( {\left| {\chi _{{mk}}^{2} - \chi _{{nl}}^{2}} \right|} \right)} \right),$(4)
${{\omega }_{{m{\kern 1pt} 'n{\kern 1pt} '}}} = \frac{1}{\hbar }\left( {\frac{{{{\hbar }^{2}}}}{{2{{m}_{e}}{{a}^{2}}}}\left( {\left| {\chi _{{m{\kern 1pt} 'k{\kern 1pt} '}}^{2} - \chi _{{n{\kern 1pt} 'l{\kern 1pt} '}}^{2}} \right|} \right)} \right),$(5)
${{\omega }_{{m{\kern 1pt} 'n}}} = \frac{1}{\hbar }\left( {e{{E}_{{g1}}} + \frac{{{{\hbar }^{2}}}}{{2{{a}^{2}}}}\left( {\frac{{\chi _{{m{\kern 1pt} 'k{\kern 1pt} '}}^{2}}}{{{{m}_{e}}}} + \frac{{\chi _{{nl}}^{2}}}{{{{m}_{h}}}}} \right)} \right).$Правило отбора в данном случае имеет вид $k{\kern 1pt} ' - l = 0.$ Длина волны соответствующего перехода имеет вид $~~{{\lambda }_{{m{\kern 1pt} 'n{\kern 1pt} }}} = \frac{{2\pi c}}{{{{\omega }_{{m{\kern 1pt} 'n}}}}}.$ Дипольный момент внутризонного перехода в КТ, согласно [8], может быть рассчитан следующим образом:
(6)
${{\mu }_{{i - f}}} = e\left\langle {{{\psi }_{i}}\left| r \right|{{\psi }_{f}}} \right\rangle = e\int\limits_V {\psi _{i}^{*}\left( r \right)r{{\psi }_{f}}\left( r \right)dV} .$При переходе к тройному интегралу в сферических координатах данный параметр может быть рассчитан так:
где $\varepsilon $ – диэлектрическая проницаемость КТ, $r$ – радиус-вектор, определяющий расстояние носителя заряда до центра КТ, $\theta $ – азимутальный угол, $~\varphi $ – полярный угол, ${{\psi }_{i}},~$ ${{\psi }_{f}}$ – волновые функции уровней, с которого и на который осуществляется переход соответственно; $~R$ – радиус КТ; $\psi _{i}^{*}\left( {r,{\theta },{\varphi }} \right)$ – сопряженная волновая функция уровня, с которого осуществляется переход. Согласно [9] волновая функция для сферической КТ определяется следующим образом:(8а)
${{\psi }_{{nlm}}}\left( r \right) = \sqrt {\frac{2}{{{{R}^{3}}}}} \frac{{{{j}_{l}}\left( {{{k}_{{nl}}}r} \right)}}{{{{j}_{{l + 1}}}\left( {{{\chi }_{{nl}}}} \right)}}{{Y}_{{lm}}}\left( {{\Theta },\phi } \right),$либо
(8б)
${{\psi }_{{nlm}}}\left( r \right) = \sqrt {\frac{2}{r}} \frac{1}{R}\frac{{{{J}_{{l + 1{\text{/}}2}}}\left( {{{k}_{{nl}}}r} \right)}}{{{{J}_{{l + 3{\text{/}}2}}}\left( {{{\chi }_{{nl}}}} \right)}}{{Y}_{{lm}}}\left( {{\Theta },\phi } \right),$(9)
$\begin{gathered} {{\mu }_{{i - f}}} = \frac{2}{{{{R}^{2}}{{J}_{{l' + \frac{3}{2}}}}\left( {{{\chi }_{{n{\kern 1pt} 'l{\kern 1pt} '}}}} \right){{J}_{{l + \frac{3}{2}}}}\left( {{{\chi }_{{nl}}}} \right)}} \times \\ \times \,\,\int\limits_0^{2\pi } {\int\limits_0^\pi {{{Y}_{{l'm'}}}\left( {{\Theta },\phi } \right){{Y}_{{lm}}}\left( {{\Theta },\phi } \right){\text{sin}}\theta d\theta d\varphi \times } } \\ \times \,\,\int\limits_0^R {{{J}_{{l{\kern 1pt} ' + \frac{1}{2}}}}\left( {{{k}_{{n{\kern 1pt} 'l{\kern 1pt} '}}}r} \right){{J}_{{l + 1{\text{/}}2}}}\left( {{{k}_{{nl}}}r} \right){{r}^{2}}dr} , \\ \end{gathered} $(10)
${{Y}_{{lm}}}\left( {{\Theta },\phi } \right) = \frac{1}{{\sqrt {2\pi } }}{{e}^{{im\phi }}}{{{\Theta }}_{{lm}}}\left( \theta \right),$(11)
${{{\Theta }}_{{lm}}}\left( \theta \right) = {{\left( { - 1} \right)}^{m}}\sqrt {\frac{{2l + 1}}{2}\frac{{\left( {l - m} \right)!}}{{\left( {l + m} \right)!}}} P_{l}^{m}\left( {\cos \left( \theta \right)} \right),$(12)
$P_{l}^{m}\left( {\cos \left( \theta \right)} \right) = {{\sin }^{m}}\theta \frac{{{{d}^{m}}}}{{d{{{\left( {cos\theta } \right)}}^{m}}}}{{P}_{l}}\left( {{\text{cos}}\theta } \right),$При $~m = 0~$ полином $P_{l}^{m}$ совпадает с полиномом Лежандра ${{P}_{l}}$ вида:
(13)
$\begin{gathered} P_{l}^{0}\left( {\cos \left( \theta \right)} \right) = {{P}_{l}}\left( {{\text{cos}}\theta } \right) = \\ = \,\,\frac{1}{{{{2}^{l}}l!}}\frac{{{{d}^{l}}}}{{d{{{\left( {cos\theta } \right)}}^{l}}}}{{\left( {{{{\cos }}^{2}}\theta - 1} \right)}^{l}}. \\ \end{gathered} $Далее мы полагаем, что магнитное квантовое число равно m = 0, тогда:
(14a)
${{Y}_{{l0}}}\left( {{\Theta },\phi } \right) = \frac{1}{{\sqrt {2\pi } }}{{{\Theta }}_{{l0}}}\left( \theta \right),$(14б)
${{{\Theta }}_{{l0}}}\left( \theta \right) = \sqrt {\frac{{2l + 1}}{2}} {{P}_{l}}\left( {\cos \left( \theta \right)} \right).$Дипольный момент межзонного перехода может быть приблизительно оценен исходя из соотношения [11]:
(15)
$\mu _{{bb}}^{2} = \frac{{{{e}^{2}}}}{{6{{m}_{0}}{{\omega }_{{m{\kern 1pt} 'n}}}^{2}}}\left( {\frac{{{{m}_{0}}}}{{{{m}_{e}}}} - 1} \right)\frac{{{{E}_{{m{\kern 1pt} 'n}}}\left( {{{E}_{{m{\kern 1pt} 'n}}} + {{\Delta }_{0}}} \right)}}{{{{E}_{{m{\kern 1pt} 'n}}} + {{2{{\Delta }_{0}}} \mathord{\left/ {\vphantom {{2{{\Delta }_{0}}} 3}} \right. \kern-0em} 3}}},$Рис. 1.
а – Вид окна программного модуля для расчета параметров полупроводниковых КТ; б – зависимости энергии межзонного перехода $1S\left( e \right) \to 1S\left( h \right)$ CdSe КТ от радиуса, рассчитанные в сравнении с [6].
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОВОДИМОСТИ ГРАФЕНА И МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ ВО ВРЕМЕННОЙ ОБЛАСТИ
В качестве основы для формирования межузловых соединений в плазмонных схемах могут быть выбраны как металлические, так и более перспективные, графеновые волноводы. Графен [13] является двумерным материалом на основе гексагональной решетки атомов углерода толщиной в один атом. Уникальной особенностью такой структуры является возможность наблюдения высокотемпературной проводимости как в чистом материале [14], так и его допированных модификациях [15], что может сделать графен основой интегральных схем будущего. Преимущество графена как основы для плазмонных схем заключается в возможности достижения предельной локализации электромагнитной волны на масштабах в несколько нм [16]. Электропроводность графена на частоте $\omega $ может быть описана на основе формализма Кубо [17] и определяется выражением:
(16)
$\begin{gathered} \sigma \left( {\omega ,{{\mu }_{с}},\tau ,T} \right)~\,\, = \,\,i\frac{{\frac{{8{{\sigma }_{0}}kT}}{h}}}{{\omega + i\frac{1}{\tau }}}\left( {\frac{{{{\mu }_{с}}}}{{kT}}~\,\, + \,\,2{\text{ln}}\left( {{{e}^{{ - \frac{{{{\mu }_{с}}}}{{kT}}}}}~\,\, + \,\,1} \right)} \right)~\,\, + ~ \\ + \,\,i\frac{{{{\sigma }_{0}}}}{\pi }{\text{ln}}\left( {\frac{{2\left| {{{\mu }_{с}}} \right| - \left( {\omega + i\frac{1}{\tau }} \right)\hbar }}{{2\left| {{{\mu }_{с}}} \right| + \left( {\omega + i\frac{1}{\tau }} \right)\hbar }}} \right), \\ \end{gathered} $(17)
$\varepsilon \left( \omega \right) = {{\varepsilon }_{r}}\left( \omega \right) - {{{{\sigma }_{i}}\left( \omega \right)} \mathord{\left/ {\vphantom {{{{\sigma }_{i}}\left( \omega \right)} {\left( {{{\varepsilon }_{0}}\omega {\Delta }} \right)}}} \right. \kern-0em} {\left( {{{\varepsilon }_{0}}\omega {\Delta }} \right)}} + {{i{{\sigma }_{r}}\left( \omega \right)} \mathord{\left/ {\vphantom {{i{{\sigma }_{r}}\left( \omega \right)} {\left( {{{\varepsilon }_{0}}\omega {\Delta }} \right)}}} \right. \kern-0em} {\left( {{{\varepsilon }_{0}}\omega {\Delta }} \right)}},$(18)
$\varepsilon \left( \omega \right) = {{1 + {{\sigma }_{{v}}}} \mathord{\left/ {\vphantom {{1 + {{\sigma }_{{v}}}} {\left( {i\omega {{\varepsilon }_{0}}} \right)}}} \right. \kern-0em} {\left( {i\omega {{\varepsilon }_{0}}} \right)}} = 1 + {{{{\sigma }_{0}}} \mathord{\left/ {\vphantom {{{{\sigma }_{0}}} {\left( {i\omega {{\varepsilon }_{0}}\left( {1 + i\omega \tau } \right)} \right)}}} \right. \kern-0em} {\left( {i\omega {{\varepsilon }_{0}}\left( {1 + i\omega \tau } \right)} \right)}},$(19)
${{\beta }_{{{\text{ППП}}}}}\left( \omega \right) = {{k}_{0}}\sqrt {1 - {{{\left( {{{2c{{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{2c{{\varepsilon }_{0}}} {{{{\tilde {\sigma }}}_{{intra}}}}}} \right. \kern-0em} {{{{\tilde {\sigma }}}_{{intra}}}}}} \right)}}^{2}}} ,$Для численного моделирования формирования ППП на графене использовался метод FDTD для уравнений Максвелла вида [1]:
(20a)
$\frac{{\partial D}}{{\partial t}} = \nabla \times H,\,\,\,\frac{{\partial H}}{{\partial t}} = - \frac{1}{\mu }\nabla \times E,$(20б)
$D\left( \omega \right) = {{c}_{0}}\varepsilon _{r}^{*}\left( \omega \right)E\left( \omega \right),$где $\varepsilon _{r}^{*}$ и ${{c}_{0}}$ – относительная диэлектрическая проницаемость среды и скорость света, D – плотность потока, E – напряженность электрического поля, H – напряженность магнитного поля, μ – магнитная проницаемость среды. При переходе к нормированным параметрам $\tilde {E} = \sqrt {{{{{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}} {{{\mu }_{0}}}}} \right. \kern-0em} {{{\mu }_{0}}}}} E$ и $\tilde {D} = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} D}}} \right. \kern-0em} {\sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} D}}$ уравнения Максвелла перепишутся в следующей форме:
(21а)
$\frac{{\partial{ \tilde {D}}}}{{\partial t}} = \frac{1}{{\sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} }}\nabla \times H = {{c}_{0}}\nabla \times H,$(21б)
$\frac{{\partial {{H}_{z}}}}{{\partial t}} = - \frac{1}{{\sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} }}\nabla \times \tilde {E} = {{c}_{0}}\nabla \times \tilde {E},$(21в)
$\tilde {D}\left( \omega \right) = \varepsilon _{r}^{*}\left( \omega \right)\tilde {E}\left( \omega \right).$Уравнения Максвелла для поперечной (ТЕМ) моды, когда поляризованная волна распространяется в направлении z, имеют вид:
(22a)
$\frac{{\partial {{{\tilde {D}}}_{y}}}}{{\partial t}} = {{c}_{0}}\frac{{\partial {{H}_{x}}}}{{\partial z}},\,$(22б)
$\frac{{~~~\partial {{H}_{x}}}}{{\partial t}} = {{c}_{0}}\frac{{\partial {{{\tilde {E}}}_{y}}}}{{\partial z}}.$Дискретизация уравнения Максвелла с использованием метода центральной производной и шагом ${\Delta }t = {{{\Delta }z} \mathord{\left/ {\vphantom {{{\Delta }z} {2{{c}_{0}}}}} \right. \kern-0em} {2{{c}_{0}}}},$ где ${\Delta }z$ – пространственный размер (рис. 2), дает:
(23а)
$\begin{gathered} \tilde {D}_{y}^{{n + \frac{1}{2}}}\left( k \right) = \tilde {D}_{y}^{{n - \frac{1}{2}}}\left( k \right) + \\ + \,\,\frac{1}{2}\left[ {H_{x}^{n}\left( {k + \frac{1}{2}} \right) - H_{x}^{n}\left( {k - \frac{1}{2}} \right)} \right], \\ \end{gathered} $(23б)
$\begin{gathered} H_{x}^{{n + 1}}\left( {k + \frac{1}{2}} \right) = H_{x}^{{n - 1}}\left( {k + \frac{1}{2}} \right) + \\ + \,\,\frac{1}{2}\left[ {\tilde {E}_{y}^{{n + \frac{1}{2}}}\left( {k + 1} \right) - \tilde {E}_{y}^{{n + \frac{1}{2}}}\left( k \right)} \right]. \\ \end{gathered} $Электрическое поле вычисляется по формуле (21в). Объединив уравнения (18) и (21в), получим:
(24)
${{D}_{y}}\left( \omega \right) = \left\{ {1 + {{{{\sigma }_{0}}} \mathord{\left/ {\vphantom {{{{\sigma }_{0}}} {\left( {j\omega {{\varepsilon }_{0}}} \right)}}} \right. \kern-0em} {\left( {j\omega {{\varepsilon }_{0}}} \right)}} - {B \mathord{\left/ {\vphantom {B {\left( {1 + j\omega \tau } \right)}}} \right. \kern-0em} {\left( {1 + j\omega \tau } \right)}}} \right\}{{\tilde {E}}_{y}},$(25а)
$\begin{gathered} \tilde {E}_{y}^{{n + \frac{1}{2}}}\left( k \right) = \\ = {{\left( {\tilde {D}_{y}^{{n + \frac{1}{2}}}\left( k \right) + {{I}^{{n - \frac{1}{2}}}}\left( k \right) + {{e}^{{{{ - {\Delta }t} \mathord{\left/ {\vphantom {{ - {\Delta }t} \tau }} \right. \kern-0em} \tau }}}}{{S}^{{n - \frac{1}{2}}}}\left( k \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\tilde {D}_{y}^{{n + \frac{1}{2}}}\left( k \right) + {{I}^{{n - \frac{1}{2}}}}\left( k \right) + {{e}^{{{{ - {\Delta }t} \mathord{\left/ {\vphantom {{ - {\Delta }t} \tau }} \right. \kern-0em} \tau }}}}{{S}^{{n - \frac{1}{2}}}}\left( k \right)} \right)} {M\left( k \right)}}} \right. \kern-0em} {M\left( k \right)}}, \\ \end{gathered} $(25б)
${{I}^{{n + \frac{1}{2}}}}\left( k \right) = {{I}^{{n - \frac{1}{2}}}}\left( k \right) + N\left( k \right)\tilde {E}_{y}^{{n + \frac{1}{2}}}\left( k \right),$(25в)
${{S}^{{n + \frac{1}{2}}}}\left( k \right) = {{S}^{{n - \frac{1}{2}}}}\left( k \right){{e}^{{{{ - {\Delta }t} \mathord{\left/ {\vphantom {{ - {\Delta }t} \tau }} \right. \kern-0em} \tau }}}} + L\left( k \right)\tilde {E}_{y}^{{n + \frac{1}{2}}}\left( k \right),$(26а)
$\begin{gathered} \tilde {D}_{z}^{{n + \frac{1}{2}}}\left( {i,j} \right) = \tilde {D}_{z}^{{n - \frac{1}{2}}}\left( {i,j} \right) + \\ + \,\,\frac{1}{2}\left[ {H_{y}^{n}\left( {i - \frac{1}{2},j} \right)--H_{x}^{n}\left( {i,j + \frac{1}{2}} \right) - H_{x}^{n}\left( {i,j - \frac{1}{2}} \right)} \right], \\ \end{gathered} $(26б)
$\begin{gathered} H_{x}^{{n + 1}}\left( {i,j + \frac{1}{2}} \right) = H_{x}^{n}\left( {i,j + \frac{1}{2}} \right) - \\ - \,\,\frac{1}{2}\left[ {\tilde {E}_{z}^{{n + \frac{1}{2}}}\left( {i,j + 1} \right) - \tilde {E}_{z}^{{n + \frac{1}{2}}}\left( {i,j} \right)} \right], \\ \end{gathered} $(26в)
$\begin{gathered} H_{y}^{{n + 1}}\left( {i + \frac{1}{2},j} \right) = H_{y}^{n}\left( {i + \frac{1}{2},j} \right) + \\ + \,\,\frac{1}{2}\left[ {\tilde {E}_{z}^{{n + \frac{1}{2}}}\left( {i + 1,j} \right) - \tilde {E}_{z}^{{n + \frac{1}{2}}}\left( {i,j} \right)} \right]. \\ \end{gathered} $Предварительное моделирование формирования и распространения поверхностных электромагнитных волн проводилось с использованием в качестве источника магнитного диполя в виде:
(27)
$\begin{gathered} H\left( {t,x = 0,y = 0,z} \right) = \\ = {{H}_{0}}\sin \left( {2\pi ft} \right) = {{H}_{0}}\sin \left( {{{\omega }_{1}}t} \right). \\ \end{gathered} $Изначально была проведена калибровка реализованного метода FDTD по известным результатам работ [1, 2, 16]. Далее было проведено полное моделирование поля с источником (27) на длинах волн 2, 4 и 8 мкм для структуры из двух графеновых листов и показано формирование ППП в системе (рис. 3). Для удобства было разработано онлайн-приложение, в котором на стороне пользователя находится построитель макета двумерных плазмонных схем, в то время как блок численного расчета и моделирования электромагнитного поля реализован на стороне сервера. Разработанные подходы и их реализация в настоящем варианте не позволяют проводить полномасштабное моделирование процессов резонансного взаимодействия КТ и ППП в графене, т.е. моделирование для нескольких КТ вблизи графена, что является темой последующих исследований.
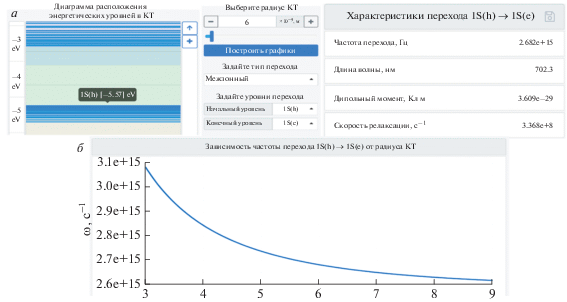
Рис. 3.
Вид части основной рабочей html-страницы программного модуля в режиме построения распределения интенсивностей для ТЕ-мод. Пространственное распределение ${{E}_{y}}$ для ППП, формируемых на паре графеновых листов с параметрами ${{\mu }_{c}} = 0.6$ эВ, $\tau = 0.9$ пс, длина волны источника ${{\lambda }_{0}} = 8.0$ мкм, диэлектрическая проницаемость окружения ${{\varepsilon }_{d}} = {\text{\;}}1$.
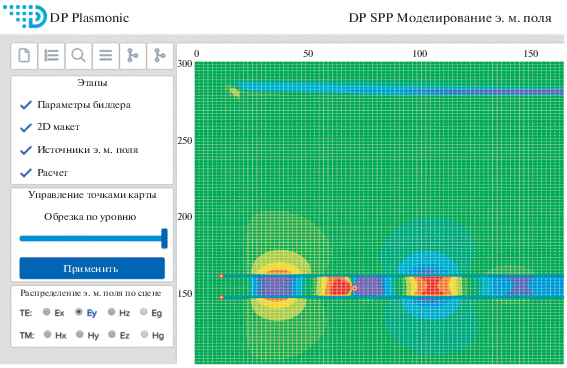
Вместе с тем, версия программы, адаптированная для работы с тонкими пленками произвольных проводящих материалов, позволила провести полное полевое моделирование процессов формирования и выявить особенности управления поверхностными плазмон-поляритонами в планарных устройствах на основе наноструктурированных пленок золота. В перспективе запланировано расширение программы для реализации трехмерного моделирования и анализа как отдельных локализованных плазмон-поляритонных структур [18], так и целых массивов на их основе [19].
ЗАКЛЮЧЕНИЕ
В работе рассмотрены математические модели и численные алгоритмы, необходимые для проектирования функциональных устройств на основе двумерных материалов и полупроводниковых квантовых точек. В частности, разработаны модели для расчета основных оптических характеристик КТ на основе полупроводниковых соединений A3B5 и A2B6. Составлена и программно реализована численная модель метода конечных разностей во временной области для моделирования распространения плазмон-поляритонных мод в плазмонных структурах на основе графена. Проведена проверка корректности работы алгоритмов на основе сравнения результатов симуляции с данными экспериментальных и теоретических работ.
Работа выполнена в рамках договора 2226ГС1/ 37022 с фондом содействия инновациям и поддержана грантом Российского научного фонда № 19-72-20154.
Список литературы
Sarker P.C., Rana Md.M., Sarkar A.K. // Optik. Int. J. Light Electron. Opt. 2017. V. 144. P. 1.
Hossain Md.B., Rana Md.M. // ICEEICT. 2015. P. 1.
Bel Haj Mohamed N., Haouari M., Zaaboub Z. et al. // J. Nanopart. Res. 2014. V. 16. P. 2242.
von Grunberg H.H. // Phys. Rev. B. 1997. V. 55. P. 2293.
Дроздов К.А. Оптические и фотоэлектрические свойства композитных структур на основе пористой матрицы SnO2 и гетероэпитаксиальных нанокристаллов CdSe/CdS. Дисс. … канд. физ.-мат. наук. Москва: МГУ, 2015.
Abd A.N. // Quantum dots CdSe/PSi/Si photodetector. Dr. Phil. on Phys. thesis. Baghdad: University of Al-Mustansiriyah, 2015.
Koole R., Groeneveld E., Vanmaekelbergh D. et al. Size effects on semiconductor nanoparticles. Berlin, Heidelberg: Springer, 2014. P. 13.
Weber A. Intraband spectroscopy of semiconductor quantum dots. Dr. Phil. thesis. Würzburg: Julius-Maximilians Universität, 1998.
Гапоненко С.В., Розанов Н.Н., Ивченко Е.Л. и др. Оптика наноструктур. СПб.: Недра, 2005. 326 с.
Градштейн И.С., Рыжик И.М. Табл. интегралов, сумм, рядов и произведений. 4-е изд. М.: Физматгиз, 1963. 1100 с.
Melikyan A.O., Minasyan G.R. // Semiconductors. 2000. V. 34. № 4. P. 386.
http://plazm.expertpro.online.
Novoselov K.S., Geim A.K., Morozov S.V. et al. // Science. 2004. V. 306. № 5696. P. 666.
Di Bernardo A., Millo O., Barbone M. et al. // Nat. Commun. 2017. V. 8. Art. № 14024.
Ichinokura S., Sugawara K., Takayama A. et al. // ACS Nano. 2016. V. 10. № 2. P. 2761.
Wang B., Zhang X., Yuan X. et al. // Appl. Phys. Lett. 2012. V. 100. Art. № 131111.
Aliofkhazraei M., Ali N., Milne W.I. et al. Graphene science handbook. Electrical and optical properties. Boca Raton: CRC Press, 2016. 720 p.
Dzedolik I.V., Pereskokov V. // J. Opt. Soc. Amer. A. 2016. V. 33. № 5. P. 1004.
Dzedolik I.V., Lapayeva S., Pereskokov V. // J. Opt. 2016. V. 18. № 7. Art. № 074007.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая