Известия РАН. Серия физическая, 2020, T. 84, № 4, стр. 508-514

ВВЕДЕНИЕ

Основной целью исследования столкновений тяжелых ионов является изучение уравнения состояния ядерного вещества (EOS – equation of state). Наряду с молекулярной динамикой и динамическим уравнением Власова эффективным методом описания взаимодействия тяжелых ионов при средних и промежуточных энергиях является ядерная гидродинамика (см., например, [1]). Как правило, используется равновесное EOS [1], предполагающее установление в системе локального термодинамического равновесия. В работах [2, 3] предложено при высоких энергиях использовать гибридную модель, которая включает в себя быструю неравновесную стадию и последующее описание динамики ядро–ядерного столкновения на основе равновесной релятивистской гидродинамики идеальной жидкости. В наших работах [4–11] было показано, что локальное термодинамическое равновесие в процессе столкновений тяжелых ионов устанавливается не сразу, поскольку на стадии сжатия важна неравновесная компонента функции распределения, приводящая к формированию бесстолкновительной ударной волны.

В настоящей работе используется кинетическое уравнение для нахождения функции распределения нуклонов, которое решается совместно с уравнениями гидродинамики, представляющими по существу локальные законы сохранения массы, импульса и энергии. Поскольку основную информацию о EOS несут испускаемые вторичные частицы (нуклоны, фрагменты, пионы), необходимо знать дифференциальные сечения испускания этих частиц. В развитие наших работ [11–13], посвященных энергетическим спектрам протонов и фрагментов, в данной работе анализируются энергетические спектры подпороговых пионов.

Под подпороговым рождением понимают образование $\pi $-мезонов при энергиях ниже порога рождения пионов ${{E}_{{NN}}}$ в свободных нуклон-нуклонных столкновениях. Абсолютный порог рождения пионов составляет соответственно в нуклон-нуклонных столкновениях ${{E}_{{NN}}} = 2{{m}_{\pi }}$ +  $\frac{{m_{\pi }^{2}}}{{2m}} \approx 290$ МэВ, в нуклон-ядерных ${{E}_{{NA}}} \approx {{m}_{\pi }} \approx 140$ МэВ, в ядро-ядерных ${{E}_{{BA}}}$ = $\frac{{m_{\pi }^{2} + 2(A + B){{m}_{\pi }}m}}{{2ABm}}$ ≈ 20 МэВ при $A = B = 12,$ где ${{m}_{\pi }}$ – масса пиона, $m$ – масса нуклона. Это выражение для абсолютной пороговой энергии получено из сравнения релятивистских инвариантов $J = {{E}^{2}} - {{P}^{2}}$ ($E$ – полная энергия, $P$ – полный импульс) до и после столкновения в пренебрежении энергией связи пиона.

Понижение порога рождения пионов при столкновении тяжелых ионов происходит благодаря коллективным эффектам и внутреннему движению нуклонов. Учет этих эффектов естественно проводить в гидродинамическом подходе, явно включающем многочастичный характер сталкивающихся тяжелых ионов. При низких подпороговых энергиях нужно модифицировать гидродинамику учетом неравновесного EOS, описывающего переход от первоначального неравновесного состояния к состоянию локального термодинамического равновесия.

В таком подходе к описанию временной эволюции образующегося горячего пятна (hot spot) рассмотрены стадия сжатия и стадия расширения с учетом найденной нами ядерной вязкости. Вычисленные энергетические спектры пионов, образующихся в столкновениях ядер, как одинаковых, так и различающихся по массе, при подпороговых энергиях 84 и 94 МэВ/нуклон, находятся в согласии с имеющимися экспериментальными данными [14] и [15], соответственно.

1. УРАВНЕНИЯ НЕРАВНОВЕСНОГО ГИДРОДИНАМИЧЕСКОГО ПОДХОДА

При энергиях сталкивающихся тяжелых ионов менее 300 МэВ/нуклон – порога рождения пионов в свободных нуклон-нуклонных столкновениях – мы используем кинетическое уравнение для нахождения нуклонной функции распределения $f(\vec {r},\vec {p},t)$ ($\vec {r}({{x}_{1}},{{x}_{2}},{{x}_{3}})$ – пространственная координата, $\vec {p}({{p}_{1}},{{p}_{2}},{{p}_{3}})$ – импульс, $t$ – время) [11, 12]:

где ${{f}_{0}}(\vec {r},\vec {p},t)$ – локально равновесная функция распределения, $\tau $ – время релаксации, $W(\rho )$ – зависящий от плотности $\rho $ одночастичный самосогласованный потенциал, $m$ – масса нуклона. Уравнение (1) нужно решать совместно с уравнениями гидродинамики

для нахождения плотности $\rho = g\int {f\frac{{{{d}^{3}}\vec {p}}}{{{{{(2\pi \hbar )}}^{3}}}}} ,$ плотности i-й компоненты импульса $m\rho {{\upsilon }_{i}}$ = $g\int {{{p}_{i}}f\frac{{{{d}^{3}}\vec {p}}}{{{{{(2\pi \hbar )}}^{3}}}}} ,$ плотности внутренней энергии $e = {{e}_{{kin}}} + {{e}_{{int}}},$ где

тензор давления ${{P}_{{ij}}} = {{P}_{{kin,ij}}} + {{P}_{{int}}}{{\delta }_{{ij}}},$ где

Здесь по повторяющимся индексам $i,j = 1,2,3$ всюду предполагается суммирование, ${{\delta }_{{ij}}}$ – символ Кронекера, вектор плотности теплового потока ${{Q}_{i}}$ = $g\int {\frac{{({{p}_{i}} - m{{\upsilon }_{i}})}}{m}} \frac{{{{{(\vec {p} - m\vec {\upsilon })}}^{2}}}}{{2m}}$$f\frac{{{{d}^{3}}\vec {p}}}{{{{{(2\pi \hbar )}}^{3}}}},$ $\hbar $ – постоянная Планка, $g = 4$ – спин-изоспиновый фактор. Члены взаимодействия для плотности энергии ${{e}_{{int}}}$ и давления ${{P}_{{int}}}$ соответственно равны

Входящий в члены взаимодействия самосогласованный потенциал $W(\rho )$ задается так же, как это делается в случае зависящих от плотности $\rho $ эффективных сил типа сил Скирма:

где три параметра $\alpha (\alpha < 0),$ $\beta (\beta > 0)$ и $\chi (\chi > 1)$ определяются заданием значений равновесной плотности ${{\rho }_{0}}$ = 0.145 фм^–3, энергии связи ${{E}_{b}}$ = –16 МэВ и модуля сжатия K = 210 МэВ. Время релаксации выбрано в форме $\tau = {\lambda \mathord{\left/ {\vphantom {\lambda {{{\upsilon }_{T}}}}} \right. \kern-0em} {{{\upsilon }_{T}}}},$ где $\lambda = {1 \mathord{\left/ {\vphantom {1 {\sigma \rho }}} \right. \kern-0em} {\sigma \rho }}$ – средняя длина свободного пробега нуклонов, $\sigma $ ≈ 40 мб – полное элементарное сечение нуклон-нуклонного взаимодействия, ${{\upsilon }_{T}}$ – средняя скорость теплового движения нуклонов. Здесь использована более традиционная форма для времени релаксации $\tau ,$ отличающаяся от предложенной в [16] и использованной нами ранее [11, 12].

Уравнения (1)–(4) с учетом выражений (5)–(8) описывают динамику столкновения ядер и составляют основу нашего подхода.

2. ГИДРОДИНАМИЧЕСКАЯ СТАДИЯ

Описание временной эволюции сталкивающихся ядер мы упрощаем, выделяя стадии сжатия, расширения и разлета образующегося горячего пятна hot spot. На стадии сжатия в процессе удара по системе в противоположные стороны распространяются бесстолкновительные ударные волны с изменяющимся фронтом [5–12], приводя к образованию сжатой и разогретой области “hot spot” – шара радиуса R.

Расширение hot spot происходит в соответствии со следующими из (2)–(4) уравнениями гидродинамики

для радиального движения нуклонной плотности $\rho (r,t),$ скорости $\upsilon (r,t),$ плотности энергии $e(r,t)$ и давления $P(r,t).$ Тепловой поток $Q = 0$ для локально равновесной функции распределения.

В приближении однородной, но зависящей от времени, плотности hot spot $\rho (r,t) = \rho (t)$ из уравнения (9) находим поле скоростей:

где $R(t)$ – радиус hot spot, а ${{R}_{1}}(t)$ – определяемый из решения уравнений радиус излома поля скоростей, $\dot {R}(t)$ и ${{\dot {R}}_{1}}(t)$ – производные по времени (скорости), которые также находятся из уравнений.

После интегрирования уравнений (10), (11) по объему hot spot получается система обыкновенных интегро-дифференциальных уравнений, которую решают численно. Эти уравнения имеют вид:

где

Здесь $A = \rho V$ – массовое число hot spot, $V = \frac{{4\pi }}{3}{{R}^{3}}$ – его объем, ${{E}_{h}}$ – его энергия, $x = {{{{R}_{1}}} \mathord{\left/ {\vphantom {{{{R}_{1}}} R}} \right. \kern-0em} R}.$

Однако в этих уравнениях не учтено отклонение функции распределения $f(\vec {r},\vec {p},t)$ от локально равновесной ${{f}_{0}}(\vec {r},\vec {p},t).$ Выражая из правой части уравнения (1) $f(\vec {r},\vec {p},t)$ через левую часть, находим:

где $I$ – зависящий от температуры $T$ член. При получении (20) в левую часть уравнения (1) вместо $f(r,\vec {p},t)$ мы подставляли ${{f}_{0}}$ ($\rho (r,t),$ $U(r,\vec {p},t),$ $T(r,t)$) с учетом уравнений (9)–(11), где $U = \frac{{{{{(\vec {p} - m\vec {\upsilon })}}^{2}}}}{{2m}}.$ При этом для уравнения (1) мы проводили усреднение по объему hot spot, а плотность $\rho (r,t),$ температура $T(r,t)$ и тепловой член $I(r,t)$ на стадии расширения считались однородными. независящими от радиуса $r$ функциями времени $t.$ Подставляя выражение (20) в (5) и (6), находим поправки к кинетическим членам плотности энергии ${{e}_{{kin}}}$ и давления ${{P}_{{kin}}}{\text{:}}$ где ${{e}_{{0,kin}}} = {{e}_{F}} + I,$ ${{P}_{{0,kin}}} = \frac{2}{3}{{e}_{{0,kin}}}$ – равновесные кинетические части плотности энергии и давления, ${{e}_{F}} = \frac{3}{{10}}\frac{{{{\hbar }^{2}}}}{m}{{\left( {\frac{3}{2}{{\pi }^{2}}\rho } \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}\rho $ – фермиевская часть плотности энергии, $\eta = \frac{4}{3}\left( {{{P}_{{0,kin}}} + \frac{5}{6}{{e}_{F}}} \right)\tau $ – коэффициент вязкости.

Следующие поправочные члены оказываются на порядок меньше, и они не учитываются. Тепловой поток $Q = 0.$ После подстановки поправок для ${{e}_{{kin}}}$ и ${{P}_{{kin}}}$ в уравнения (9)–(11) изменяются входящие в выражения (14) и (19) члены:

Эти члены оказывают существенное влияние на процесс расширения hot spot, замедляя его, т.к. в рассматриваемой области энергий ${{E}_{0}}$ ≈ ≈ 100 МэВ/нуклон при характерном ядерном размере l ≈ 3 фм число Рейнольдса невелико $Re = \frac{{m\rho \upsilon l}}{\eta }\sim 1$ для найденного нами коэффициента вязкости $\eta $ (формула (22)).

В нашем случае температура $T$ ≈ 20 МэВ, ${{P}_{{0,kin}}} \approx \rho T,$ $\tau \approx 3 \cdot {{10}^{{ - 23}}}$ c и коэффициент вязкости $\eta \approx $$4 \cdot {{10}^{{10}}}$ кг · м^–1 · с^–1, что по порядку величины совпадает с газовой оценкой $\eta \sim {{\sqrt {mT} } \mathord{\left/ {\vphantom {{\sqrt {mT} } \sigma }} \right. \kern-0em} \sigma }$ [17], если за элементарное сечение принять $\sigma $ ≈ 40 мб. При этом отношение $\frac{\eta }{s} \gg \frac{\hbar }{{4\pi }},$ где $s$ – плотность энтропии ($s\sim \rho $). То есть в нашем случае отношение $\frac{\eta }{s}$ более чем на порядок превышает предельное значение $\frac{\hbar }{{4\pi }}$ [18], достижимое, например, в состоянии кварк-глюонной плазмы.

Таким образом, в рассматриваемом диапазоне энергий коэффициент вязкости $\eta $ достаточно велик. Это уменьшает скорость разлета hot spot и увеличивает его температуру. По достижении расширяющейся ядерной системой критической плотности (плотности замораживания) $\rho *,$ определяемой из условия $\frac{{d{{P}_{{int}}}}}{{d\rho }}$ = $\rho \frac{{dW}}{{d\rho }} = 0,$ происходит формирование вторичных частиц (нуклонов, фрагментов, пионов) и их разлет.

3. ДВОЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ СЕЧЕНИЕ ИСПУСКАНИЯ ПИОНОВ. СРАВНЕНИЕ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

По достижении ядерной системой критической плотности происходит испускание пионов. Сечение испускания пионов находится из условия, что число частиц $f{{d}^{3}}\vec {p}$ и величина ${{{{d}^{3}}\vec {p}} \mathord{\left/ {\vphantom {{{{d}^{3}}\vec {p}} E}} \right. \kern-0em} E}$ являются релятивистскими инвариантами [19, 20]. В результате инклюзивное двойное дифференциальное сечение реакции A + B → $\pi $ + X равно

где $b$ – параметр удара, а функция распределения пионов имеет вид

Здесь $E$ и $\vec {p}$ – полная энергия и импульс пиона соответственно, $E = \sqrt {{{p}^{2}} + m_{\pi }^{2}} ,$ $\Omega $ – телесный угол, $\vec {\upsilon }(\vec {r},t)$ и $T(\vec {r},t)$ – поле скоростей и температура в момент разлета, являющиеся решениями уравнений гидродинамики, $\gamma = {1 \mathord{\left/ {\vphantom {1 {\sqrt {1 - {{{({\upsilon \mathord{\left/ {\vphantom {\upsilon c}} \right. \kern-0em} c})}}^{2}}} }}} \right. \kern-0em} {\sqrt {1 - {{{({\upsilon \mathord{\left/ {\vphantom {\upsilon c}} \right. \kern-0em} c})}}^{2}}} }}$ – лоренц-фактор, химический потенциал пионов $\mu = 0,$ т. к. число пионов не задано. Введенный в (25) фактор $G(b)$ = ${{{{\sigma }_{t}}(b)} \mathord{\left/ {\vphantom {{{{\sigma }_{t}}(b)} {{{\sigma }_{g}}(b)}}} \right. \kern-0em} {{{\sigma }_{g}}(b)}}$ учитывает отличие полного сечения от геометрического, где ${{\sigma }_{t}}(b)$ определяется как сечение образования hot spot при заданном параметре удара $b$ из двух областей перекрытия в сталкивающихся ядрах, а ${{\sigma }_{g}}(b)$ – геометрическое сечение этих областей перекрытия. Так же, как и в случае слияния двух сравнимых по размеру ядер, здесь полное сечение всегда больше геометрического.

Выражения (25), (26) относятся к пионам, испускаемым из hot spot в результате взаимодействия областей перекрытия сталкивающихся ядер. Кроме этого вклада нами учитывался вклад от испускания пионов в результате слияния неперекрывающихся областей сталкивающихся ядер. Кроме того, наряду с тепловыми пионами мы включили в расчеты вклад канала образования пионов от распада $\Delta $-изобары [22]. Также, по аналогии с протонами, мы внесли в функцию распределения испускаемых пионов поправку на микроканоническое распределение [23].

В результате мы провели сравнение с имеющимися экспериментальными данными. Так, на рис. 1 представлено сравнение вычисленных нами (сплошные линии) и экспериментальных [15] (точки) двойных дифференциальных сечений для реакций рождения ${{\pi }^{ + }}$-мезонов при столкновении под углом 90° ионов ¹⁶O c ядрами ²⁷Al (кривая 1), ⁵⁸Ni (кривая 2) и ¹⁹⁷Au (кривая 3) при энергиях ионов ¹⁶O ${{E}_{0}}$ = 94 МэВ/нуклон. Можно видеть, что при выбранных параметрах ядерного взаимодействия и с учетом найденной нами вязкости среды $\eta ,$ пропорциональной времени релаксации $\tau ,$ в пределах экспериментальных ошибок имеется согласие расчета с экспериментом. В случае большей вязкости с временем релаксации ${{\tau }_{1}},$ в полтора раза бόльшим выбранного нами $\tau .$

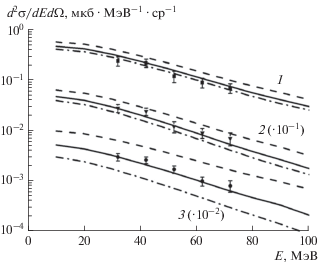
τ₁ = (3/2)τ, расчетные кривые (штриховые линии) идут заметно выше экспериментальных точек, а в случае ${{\tau }_{2}},$ в полтора раза меньшим временем релаксации τ₂ = (2/3)τ, расчетные кривые (штрих-пунктирные линии) находятся ниже экспериментальных точек. При этом влияние вязкости на величину вычисляемого сечения испускаемых пионов оказывается сильнее для более ассиметричных комбинаций сталкивающихся ядер, когда вклад от испускания пионов из hot spot преобладает. Таким образом, инклюзивные спектры пионов в ассиметричных ядерных столкновениях могут быть использованы для измерения вязкости ядерной среды.

На рис. 2 приведено сравнение расчетов (сплошные линии) с экспериментальными данными [15] (точки) для реакции ¹⁶O + ²⁷Al → ${{\pi }^{ + }}$ + X при энергии ионов ¹⁶O 94 МэВ/нуклон под углами испускания пионов 70° (кривая 1), 90° (кривая 2) и 120° (кривая 3). При неизменных параметрах расчета имеется согласие с экспериментальными данными. Вклад в выход пионов от распада $\Delta $-изобары проявляется на более высокоэнергетических хвостах экспериментального спектра при энергиях пионов $E$ ~ 120 МэВ, поэтому он не заметен на рис. 1, 2.

На рис. 3–5 представлено сравнение вычисленных нами (сплошные линии) и экспериментальных [14] (гистограммы) двойных дифференциальных сечений испускания ${{\pi }^{0}}$-мезонов в реакциях ¹²С + ²³⁸U → ${{\pi }^{0}}$ + X (кривые 1) и ¹²С + ¹²С → ${{\pi }^{0}}$ + X (кривые 2) при энергии налетающих ядер ¹²С 84 МэВ/нуклон под углами 0° (рис. 3), 90° (рис. 4) и 180° (рис. 5). Как видно, эти рисунки в целом демонстрируют согласие расчетов с экспериментальными данными [14]. Наплыв под углом 0° и выбросы на “хвосте” экспериментального энергетического спектра под углом 90° и 180° для реакции ¹²С + ²³⁸U (гистограммы на рис. 3, 4, 5) обусловлены вкладом от распада $\Delta $-изобары, и они неплохо воспроизводятся в расчете. Во всех рассмотренных иллюстрациях согласие расчета с экспериментом достигнуто без введения подгоночных параметров и оказывается более удачным по сравнению с нашими предыдущими работами [20, 21].

ЗАКЛЮЧЕНИЕ

Таким образом, в настоящей работе получила дальнейшее развитие идея использовать при описании столкновений тяжелых ионов гидродинамический подход с неравновесным уравнением состояния. С теми же фиксированными параметрами уравнения состояния и в том же подходе, как и в предыдущих работах [11–13], посвященных описанию дифференциальных сечений образования протонов и легких фрагментов, описаны дифференциальные сечения рождения подпороговых пионов в столкновениях тяжелых ионов.

Новым по сравнению с предыдущими работами явилось включение в рассмотрение эффектов ядерной вязкости, найденной нами в релаксационном τ-приближении для кинетического уравнения. Это не добавило новых параметров при описании временной эволюции ядерных столкновений. Время релаксации $\tau ,$ определяющее коэффициент ядерной вязкости $\eta ,$ найдено традиционно и не является подгоночным параметром. При описании испускания протонов и фрагментов учет вязкости среды оказался несущественным, а пионы оказываются весьма чувствительными к величине вязкости.

При вычислении сечений существенным было выделить испускание пионов после временной эволюции образующегося горячего пятна hot spot и учесть испускание частиц при слиянии “спектаторов” (неперекрывающихся областей сталкивающихся ядер). Это позволило описать дифференциальные сечения испускания пионов при столкновениях различных комбинаций сталкивающихся ядер. Выделение этой особенности нашего подхода может быть полезно при сравнении с другими механизмами рождения пионов в столкновениях тяжелых ионов, например [24, 25], основанными на решении динамического уравнения Власова–Улинга–Уленбека. В этих работах рассматривают диапазон более высоких энергий сталкивающихся тяжелых ионов (выше 300 МэВ/нуклон) и включают в описание рождение пионов посредством рождения $\Delta $-изобар. В данной работе при подпороговых энергиях мы этот канал включили, не ограничившись рождением только тепловых пионов. Наряду с тепловыми пионами этот канал проявляется на высокоэнергетических “хвостах” спектров подпороговых пионов.