Известия РАН. Серия физическая, 2020, T. 84, № 5, стр. 733-736

Расчет распределения электрического поля в измерительной ячейке для получения импеданс-спектров трехмерных клеточных моделей

Т. Н. Герасименко^1, *, С. В. Никулин^1, 2, О. В. Киндеева¹, В. А. Петров¹, Д. А. Сахаров¹

¹ Общество с ограниченной ответственностью “Научно-технический центр “БиоКлиникум”
Москва, Россия

² Федеральное государственное автономное образовательное учреждение высшего профессионального образования “Дальневосточный федеральный университет”
Владивосток, Россия

^* E-mail: t.gerasimenko@bioclinicum.com

Поступила в редакцию 02.12.2019
После доработки 23.12.2019
Принята к публикации 27.01.2020

DOI: 10.31857/S0367676520050105

Полный текст (PDF)

Аннотация

Проведено математическое моделирование импеданс-спектров, получаемых с помощью четырехэлектродной схемы измерений в среде с дисперсией на примере трехмерной клеточной культуры. Задача решена методом конечных элементов в предположении об отсутствии индуктивных явлений в исследуемой системе в заданном диапазоне частот. Учитываются электрические характеристики электродов.

ВВЕДЕНИЕ

Импедансная спектроскопия широко используется при исследовании свойств различных материалов, в частности при исследовании биологических систем. Неинвазивность этого метода и возможность его использования в реальном времени делают его очень перспективным при исследовании in vitro культур клеток [1]. Трехмерная культура представляет собой клетки, выращиваемые в специальном геле, имитирующем физиологическое микроокружение. Такие культуры широко используются в различных областях биологии и медицины, в частности при создании так называемых “органов-на-чипе”. Изменение импеданса клеточной системы с частотой позволяет получить информацию о количестве клеток, их свойствах и функциональном состоянии. Однако, для внедрения этой технологии в микрофлюидные устройства необходимы предварительные оценки, которые позволят правильно подобрать форму измерительной ячейки, расположение электродов и скорректировать точность прибора. Проведению такого теоретического расчета посвящена данная работа.

Предполагалось, что для измерений используется четырехэлектродная схема, в которой силовые (WE – рабочий, CE – противоэлектрод) и измерительные (SE1 и SE2) электроды могут быть напылены дно или на крышку ячейки.

РАСЧЕТ ИМПЕДАНСА

В общем случае распределение электрических и магнитных полей в системе описывается системой уравнений Максвелла и материальными уравнениями. Однако, в ряде случаев, в том числе и для биологических систем, в диапазоне частот, на которых проводятся измерения, характерно отсутсвие индуктивных явлений [2], что позволяет считать ротор напряженности электрического поля $\vec {E}$ равным нулю, и соотвественно, использовать для его описания только скалярный потенциал φ:

(1)

$\vec {E} = - \nabla {\varphi }.$

Такой подход, разумеется, справедлив только в рамках квазистатического приближения, реализуемого для рассматриваемой системы на частотах ${\omega } \ll \frac{{\sigma }}{{{\varepsilon }{{{\varepsilon }}_{0}}}} \approx {{10}^{9}}$ Гц [2], где σ – проводимость среды, ε – еe диэлектрическая проницаемость, ε₀ – диэлектрическая постоянная. Используя (1) и уравнение непрерывности:

(2)

${\text{0}} = {\text{div}}({\text{rot}}{\kern 1pt} \vec {H}) = {\text{div}}{\kern 1pt} \left( {\vec {j} + \frac{{\partial{ \vec {D}}}}{{\partial t}}} \right)$

с учетом материальных уравнений

(3)

$\left( {\begin{array}{*{20}{c}} {\vec {j} = - {\sigma }\nabla {\varphi }} \\ {\vec {D} = - {\varepsilon }{{{\varepsilon }}_{{\text{0}}}}\nabla {\varphi }} \end{array}} \right.$

получим уравнение на скалярный потенциал

(4)

$ - \nabla \left( {{\sigma }\nabla {\varphi } + \frac{{\partial ({\varepsilon }{{{\varepsilon }}_{0}}\nabla {\varphi })}}{{\partial t}}} \right) = 0.$

При задании граничных условий предполагалось, что на рабочем электроде (WE) потенциал зависит от времени по гармоническому закону, а противоэлектрод (CE) заземлен

(5)

$\left\{ \begin{gathered} {{\left. {{\varphi }(r,t)} \right|}_{{r \in {{\Gamma }_{{WE}}}}}} = {{{{\hat {\varphi }}}}_{0}}{{e}^{{i{\omega }t}}} \hfill \\ {{\left. {{\varphi }(r,t)} \right|}_{{r \in {{\Gamma }_{{CE}}}}}} = 0 \hfill \\ \end{gathered} \right.,$

где $\omega $ – циклическая частота, ${{{\hat {\varphi }}}_{0}}$ – комплексная амплитуда, ${{\Gamma }_{{WE}}}$ и ${{\Gamma }_{{CE}}}$ – внешние границы рабочего и противоэлектрода. Предполагалось, что к измерительным электродам (SE1 и SE2) подключен идеальный вольтметр с бесконечным сопротивлением, и ток через них равен нулю, поэтому на их границах, не соприкасающихся со средой, а также на границе среды считаем, что ${{j}_{n}} = - {\sigma }(\nabla {\varphi },\vec {n}) = 0,$ где $\vec {n}$ – внешняя нормаль к поверхности.

На границах “среда–электрод” выполняются стандартные условия равенства тангенциальных компонент напряженности и нормальных компонент индукции электрического поля. Кроме того, для удобства дальнейшего численного решения мы ввели еще одно искуственное условие, следующее из тривиального соотношения

(6)

${\text{div}}({\text{rot }}\vec {H}) = 0.$

Используя интегрирование по вспомогательному цилиндру на границе раздела, и затем устремляя высоту цилиндра к нулю, так как это делается при выводе граничных условий [2], получаем условие

(7)

$({\text{rot }}{{\vec {H}}_{m}}{\text{,}}\vec {n}) = ({\text{rot }}{{\vec {H}}_{e}}{\text{,}}\vec {n}),$

где индексы m и e относятся к среде и электродам, соотвественно. С учетом соотношений (2) и (3):

(8)

$\begin{gathered} \left( {{{{\sigma }}_{e}}\nabla {{{\varphi }}_{e}} + {{{\varepsilon }}_{e}}{{{\varepsilon }}_{0}}\frac{{\partial \nabla {{{\varphi }}_{e}}}}{{\partial t}},\vec {n}} \right) = \\ = \left( {{{\sigma }_{m}}\nabla {{{\varphi }}_{m}} + {{{\varepsilon }}_{m}}{{{\varepsilon }}_{0}}\frac{{\partial \nabla {{{\varphi }}_{m}}}}{{\partial t}},\vec {n}} \right). \\ \end{gathered} $

Потенциал с учетом условий (5) будем искать в виде

(9)

${\varphi }(t) = {\hat {\varphi }}{{e}^{{i{\omega }t}}}.$

Тогда окончательно решаемая задача будет иметь вид:

(10)

$\left( {\begin{array}{*{20}{c}} {\nabla \left( {({{{\sigma }}_{{e,m}}} + i{\omega }{{{\varepsilon }}_{{e,m}}}{{{\varepsilon }}_{0}})\nabla {{{{\hat {\varphi }}}}_{{e,m}}}} \right) = 0,\,\,\,r \in {{\Omega }_{{e,m}}}} \\ {{{{\left. {{{{{\hat {\varphi }}}}_{e}}(r)} \right|}}_{{r \in {{\Gamma }_{{WE}}}}}} = {{{{\hat {\varphi }}}}_{0}}} \\ {{{{\left. {{{{{\hat {\varphi }}}}_{e}}(r)} \right|}}_{{r \in {{\Gamma }_{{CE}}}}}} = 0} \\ {{{{\left. {\left( {({{{\sigma }}_{{e,m}}} + i{\omega }{{{\varepsilon }}_{{e,m}}}{{{\varepsilon }}_{0}})\nabla {{{{\hat {\varphi }}}}_{{e,m}}},\vec {n}} \right)} \right|}}_{{\partial \Omega /{{\Gamma }_{{WE}}},{{\Gamma }_{{CE}}}}}} = 0} \\ \begin{gathered} {{\left. {\left( {({{{\sigma }}_{e}} + i{\omega }{{{\varepsilon }}_{e}}{{{\varepsilon }}_{0}})\nabla {{{{\hat {\varphi }}}}_{e}},\vec {n}} \right)} \right|}_{{{{\Gamma }_{{e,m}}}}}}{\kern 1pt} = \hfill \\ = \,\,{{\left. {\left( {({{{\sigma }}_{m}} + i{\omega }{{{\varepsilon }}_{m}}{{{\varepsilon }}_{0}})\nabla {{{{\hat {\varphi }}}}_{m}},\vec {n}} \right)} \right|}_{{{{\Gamma }_{{e,m}}}}}} \hfill \\ \end{gathered} \end{array}} \right.$

здесь ${{\Omega }_{{e,m}}}$ – области электродов и среды с клетками, соответственно, ${{\Gamma }_{{e,m}}}$ – границы электрод-среда.

Для численного задачи (10) был использован метод конечных элементов с матрицей жесткости, модифицированной для случая комплексных переменных следующим образом:

(11)

где K_ij – элементы стандартной матрицы “жесткости” (см. напр. [4]), ${\varphi }{\kern 1pt} {\text{'}}$ и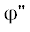

– вещественная и мнимая компоненты потенциала. Наложение граничных условий и подробное описание расчета импеданса по полученному распределению потенциала описано нами ранее [5]. Для системы линейных уравнений (11) использовался решатель MUMPS (http://mumps.enseeiht.fr), доступный по академической лицензии.

ХАРАКТЕРИСТИКИ СРЕДЫ

При определении комплексной диэлектрической проницаемости клеточной среды предполагалось, что клетки равномерно распределены в геле. Для описания их вклада в импеданс использовалась классичекая теория Максвелла–Вагнера, согласно которой комплексная диэлектрическая проницаемость суспензии при небольших объемных долях клеток описывается следующим выражением [6, 7]:

(12)

${{{\hat {\varepsilon }}}_{m}} = {{{\hat {\varepsilon }}}_{{med}}}\frac{{1 + 2\Phi {{{\hat {f}}}_{{CM}}}}}{{1 - \Phi {{{\hat {f}}}_{{CM}}}}},$

где ${{{\hat {\varepsilon }}}_{{med}}}$ – комплексная диэлектричекая проницаемость среды без клеток, $\Phi \ll 1$ – объемная доля клеток, ${{\hat {f}}_{{CM}}}$ – множитель Клаузиуса–Моссотти.

Множитель Клаузиуса–Моссотти выражается через диэлектрические проницаемости отдельной клетки ${{{\varepsilon }}_{{cell}}}$ и среды следующим образом

(13)

${{\hat {f}}_{{CM}}} = \frac{{{{{{\hat {\varepsilon }}}}_{{cell}}} - {{{{\hat {\varepsilon }}}}_{{med}}}}}{{{{{{\hat {\varepsilon }}}}_{{cell}}} + 2{{{{\hat {\varepsilon }}}}_{{med}}}}}.$

Диэлектрическая проницаемость клетки в свою очередь может быть выражена через проницаемости цитоплазмы ${{{\hat {\varepsilon }}}_{{cyt}}}$ и клеточной мембраны ${{{\hat {\varepsilon }}}_{{mem}}}$ [8]:

(14)

${{{\hat {\varepsilon }}}_{{cell}}} = {{{\hat {\varepsilon }}}_{{mem}}}\frac{{2{{{{\hat {\varepsilon }}}}_{{mem}}} + {{{{\hat {\varepsilon }}}}_{{cyt}}} - 2{\hat {\alpha }}}}{{2{{{{\hat {\varepsilon }}}}_{{mem}}} + {{{{\hat {\varepsilon }}}}_{{cyt}}} + {\hat {\alpha }}}},$

где

(15)

${\hat {\alpha }} = ({{{\hat {\varepsilon }}}_{{mem}}} - {{{\hat {\varepsilon }}}_{{cyt}}}){{\left( {\frac{D}{{D + 2d}}} \right)}^{3}}$

D = 30 мкм – диаметр клетки, $d = 5$ нм – толщина мембраны.

Объемная доля клеток вычислялась как $\Phi = {{V}_{{cell}}}{{C}_{{cells}}},$ ${{C}_{{cells}}}$ – концентрация клеток, ${{V}_{{cell}}}$ – объем одной клетки. Для расчета использовались следущие значения [6, 8]: ε_med = 80, σ_med = 0.3 См/м, ε_mem = 6.5, σ_mem =10^–8 См/м, ε_cyt = 60, σ_cyt = = 0.25 См/м, ε_e = 1.5, σ_e = 4.56 · 10⁷ См/м.

РЕЗУЛЬТАТЫ И ВЫВОДЫ

Расчет импеданс-спектров был проведен для трех вариантов измерительной ячейки при различных концентрациях клеток в среде. Объем и высота ячеек были ограничены с одной стороны инженерными особенностями конструкции микрофлюидного устройства, а с другой – необходимостью обеспечивать клетки достаточным количеством питательных веществ. Исходя из этих ограничений были рассмотрены ячейки:

1. Объемом 190 мкл и высотой 5 мм, электроды имеют форму гребенок и расположены сверху и снизу (рис. 1–1а).

Рис. 1.

Рассматриваемые клеточные ячейки: 1 – объем 190 мкл, высота 5 мм, электроды расположены сверху и снизу, 2 – объем 63 мкл, высота 1 мм, все электроды расположены на дне, 3 – объем 45 мкл, высота 1.6 мм, все электроды расположены на дне. WE – рабочий электрод, CE – противоэлектрод, SE1 и SE2 – измерительные электроды. a – трехмерное распределение потенциала, б – эквипотенциальные кривые в поперечном сечении ячеек, в – вектора плотности тока в поперечном сечении ячеек (без масштаба).

2. Объемом 63 мкл и высотой 1 мм, электроды расположены на дне (рис. 1–2 а).

Рис. 2.

Годографы импеданса в рассматриваемых ячейках для различных концентраций клеток. Для удобства сравнения смещены по вещественной оси в начало координат.

3. Объемом 45 мкл высотой 1.6 мм, с электродами на дне (рис. 1–3 а).

Соответствующие геометрии, а также примеры полученных распределений потенциала и тока на частоте 200 кГц представлены на рис. 1. Для наглядности вектора плотности тока не масштабируются. Соответствующие годографы импеданса представлены на рис. 2.

Полученные результаты подтверждают возможность использования импедансной спектроскопии для контроля за ростом трехмерной клеточной культуры в микрофлюидном устройстве. Во всех рассмотренных ячейках поле достаточно однородное, при этом максимальный уровень ожидаемого сигнала имеет место в третьем варианте измерительной ячейки, что делает его предпочтительным для изготовления.

Разработанный метод расчета импеданс-спектров позволяет легко варьировать геометрию исследуемой области, форму и число электродов. При этом электричсекие характеристики электродов также принимаются во внимание. Метод может быть применен для любой среды с заданной частотной зависимостью комплексной диэлектрической проницаемости, при условии того, что в рассматриваемом диапазоне частот справедливо квазистатическое приближение, а также допустимо пренебречь индуктивными явлениями.

Работа выполнена при поддержке Российского научного фонда (проект № 16-19-10597).

Список литературы

Srinivasan B., Kolli A.R., Esch M.B. et al. // J. Lab. Autom. 2015. V. 20. № 2. P. 107.
Preis K., Bíró O., Supancic P. et al. // IEEE Trans. Magn. 2004. V. 40. № 2. P. 1302.
Jackson J.D. Classical electrodynamics. John Wiley & Sons Inc., 1998. 626 p.
Zienkiewicz O.C., Taylor R.L. The Finite element method. V. 1. The Basis. Butterworth-Heinemann, 2000. 143 p.
Петров В.А., Герасименко Т.Н., Киндеева О.В. и др. // Изв. РАН. Сер. физ. 2020. Т. 84. № 2. С. 188; Petrov V.A., Gerasimenko T.N., Kindeeva O.V. et al. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. № 2. P. 147.
Sun T., Morgan H. // Microfluid. Nanofluid. 2010. V. 8. № 4. P. 423.
Das D., Kamil F.A., Biswas K., Das S. // RSC Adv. 2014. V. 4. Art. № 18178.
Hanai T., Asami K., Kozumi N. // Bull. Inst. Chem. Res. Kyoto Univ. 1979. V. 57. № 4. P. 297.
Canali C., Heiskanen A., Muhammad H.B. et al. // Biosens. Bioelectron. 2015. V. 63. P. 72.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал