Известия РАН. Серия физическая, 2020, T. 84, № 5, стр. 700-703
О возможности приложения матричного метода к моделированию катодолюминесценции, обусловленной широким электронным пучком в планарной многослойной полупроводниковой структуре
М. А. Степович 1, В. В. Калманович 1, *, Е. В. Серегина 2
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Калужский государственный университет имени К.Э. Циолковского”
Калуга, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный технический университет имени Н.Э. Баумана
(национальный исследовательский университет)”, Калужский филиал
Калуга, Россия
* E-mail: v572264@yandex.ru
Поступила в редакцию 02.12.2019
После доработки 23.12.2019
Принята к публикации 27.01.2020
Аннотация
Изложены результаты изучения возможностей приложения аналитического матричного метода к моделированию диффузии неравновесных неосновных носителей заряда и последующей катодолюминесценции, обусловленных широким электронным пучком в планарной многослойной структуре полупроводниковой оптоэлектроники с произвольным числом слоeв. Предложенный метод позволяет проводить расчеты с точностью, достаточной для практического использования в электронно-зондовых технологиях.
ВВЕДЕНИЕ
Для материалов полупроводниковой оптоэлектроники одним из наиболее информативных является катодолюминесцентное (КЛ) излучение, интенсивность $I$ которого на фиксированной длине волны пропорциональна концентрации $c\left( {M(x,y,z),t} \right)$ неравновесных неосновных носителей заряда (ННЗ) в точке $M(x,y,z)$ мишени в момент времени t [1]. Для стационарного случая облучения полупроводниковой мишени, реализующегося в стандартной методике КЛ измерений, можно считать, что
Здесь $\alpha $ – коэффициент поглощения монохроматического КЛ излучения в объеме полупроводника. В прямоугольной декартовой системе координат оси $x$ и $y$ обычно располагают на плоской поверхности мишени, а ось $z$ направляют вглубь полупроводника.
При использовании широкого электронного пучка для возбуждения КЛ излучения задача вычисления распределений генерированных электронами неравновесных ННЗ и интенсивности КЛ, возникающей при излучательной рекомбинации ННЗ, сводится к одномерной. В то же время даже для одномерной модели трудности реализации необходимых вычислений позволили моделировать КЛ лишь в двухслойных [2–4] и трехслойных [5] структурах.
В настоящей работе рассмотрены некоторые возможности использования аналитического матричного метода для моделирования распределений ННЗ в многослойных полупроводниковых структурах и обсуждены некоторые возможности использования полученных результатов для моделирования КЛ, возбуждаемой в таких структурах.
Изначально матричный метод, предлагаемый к рассмотрению для расчeтов КЛ, был описан применительно к задачам теплопроводности в составных пластинах в [6]. Он сводился к последовательному умножению функциональных матриц, описывающих процесс теплопроводности в рассматриваемых объектах. Однако для решения задач тепломассопереноса в многослойных средах он не получил распространения, возможно из-за того, что формулы аналитического решения получались исключительно сложными. Системы символьных вычислений в то время только начинали зарождаться и потому численные методы были предпочтительными. В частности, в [6] авторы указывают на ценность матричного метода, если использовать численные значения элементов матриц.
Ранее в наших работах аналитический матричный метод был применeн совместно с аппаратом обобщенных степеней Берса [7], что позволило успешно описать в единой форме процесс тепломассопереноса в многослойных средах с различной геометрией (плоских, осесимметричных и слоев с центральной симметрией) [8–10]. Отметим, что как численный, матричный метод применялся ранее для нахождения распределений ННЗ, генерированных широким электронным пучком, после их диффузии в однородном полупроводнике [11].
ПОСТАНОВКА ЗАДАЧИ
В случае одномерной диффузии в конечный полупроводник вдоль оси ОZ, перпендикулярной поверхности n-слойной полупроводниковой структуры $\left( {z \in \left[ {0,l} \right]} \right),$ распределение ННЗ по глубине находится как решение дифференциального уравнения
(1)
$\begin{gathered} \frac{d}{{dz}}\left( {{{D}^{{(i)}}}\left( z \right)\frac{{d\Delta {{p}^{{(i)}}}\left( z \right)}}{{dz}}} \right) - \frac{{\Delta {{p}^{{(i)}}}\left( z \right)}}{{{{\tau }^{{(i)}}}\left( z \right)}} = \\ = - {{\rho }^{{(i)}}}\left( z \right),\,\,\,\,i = \overline {1,n} , \\ \end{gathered} $с граничными условиями
(2)
$\begin{gathered} {{D}^{{(1)}}}{{\left. {\frac{{d\Delta {{p}^{{(1)}}}\left( z \right)}}{{dz}}} \right|}_{{z = 0}}} = \nu _{s}^{{(1)}}\Delta {{p}^{{(1)}}}\left( 0 \right), \\ {\text{ }}{{D}^{{(n)}}}{{\left. {\frac{{d\Delta {{p}^{{(n)}}}\left( z \right)}}{{dz}}} \right|}_{{z = l}}} = - \nu _{s}^{{(n)}}\Delta {{p}^{{(n)}}}\left( l \right). \\ \end{gathered} $Верхний индекс в скобках указывает номер слоя. Для многослойной структуры обозначим: ${{z}_{1}} = 0,$ ${{z}_{{n + 1}}} = l$ – внешние границы полупроводника, ${{z}_{2}},{{z}_{3}},...,{{z}_{n}}$ – координаты границ раздела слоёв; ${{D}^{{(i)}}},$ ${{L}^{{(i)}}},$ ${{\tau }^{{(i)}}}$ – электрофизические параметры: коэффициент диффузии, диффузионная длина и время жизни ННЗ в i-м слое соответственно, при этом ${{L}^{{(i)}}} = \sqrt {{{D}^{{(i)}}}{{\tau }^{{(i)}}}} .$ На границах полупроводника (при $z = 0$ и при $z = l$) приведенные скорости поверхностной рекомбинации ${{S}^{{(1)}}} = {{{{L}^{{(1)}}}\nu _{s}^{{(1)}}} \mathord{\left/ {\vphantom {{{{L}^{{(1)}}}\nu _{s}^{{(1)}}} {{{D}^{{(1)}}}}}} \right. \kern-0em} {{{D}^{{(1)}}}}},$ ${{S}^{{(n)}}} = {{{{L}^{{(n)}}}\nu _{s}^{{(n)}}} \mathord{\left/ {\vphantom {{{{L}^{{(n)}}}\nu _{s}^{{(n)}}} {{{D}^{{(n)}}}}}} \right. \kern-0em} {{{D}^{{(n)}}}}},$ где $\nu _{s}^{{(1)}}$ и $\nu _{s}^{{(n)}}$ – скорости поверхностной рекомбинации ННЗ в первом и n-ом слоях соответственно. Функция $\Delta {{p}^{{(i)}}}\left( z \right)$ описывает распределение по глубине в i-м слое неравновесных ННЗ, генерированных внешним энергетическим воздействием, после их диффузии в полупроводнике. Функция ${{\rho }^{{(i)}}}\left( z \right)$ – зависимость от координаты плотности ННЗ, генерированных электронным пучком в полупроводниковой мишени до их диффузии. Для широкого электронного пучка ${{\rho }^{{(i)}}}\left( z \right)$ может быть найдена из выражения для плотности энергии электронного пучка ${{\rho }^{{ * (i)}}}\left( z \right),$ выделяемой в мишени в единицу времени до начала процесса диффузии [12–14].
АЛГОРИТМ АНАЛИТИЧЕСКОГО РЕШЕНИЯ МАТРИЧНЫМ МЕТОДОМ
Введем вектор-столбцы V, W и матрицу K на каждом слое [8–11]:
(3)
$\begin{gathered} {{V}^{{(i)}}}(z) = {{K}^{{(i)}}}(z,{{z}_{i}})\left( {{{V}^{{(i)}}}({{z}_{i}}) - {{W}^{{(i)}}}({{z}_{i}})} \right) + \\ + \,\,{{W}^{{(i)}}}(z),\,\,\,\,{{z}_{i}} \leqslant z \leqslant {{z}_{{i + 1}}}. \\ \end{gathered} $Применяя с первого слоя последовательно формулу (3) и, считая контакт слоeв идеальным, т.е. ${{V}^{{(i)}}}({{z}_{{i + 1}}})$ = ${{V}^{{(i + 1)}}}({{z}_{{i + 1}}}),$ получим
(4)
$\begin{gathered} {{V}^{{(i)}}}(z) = {{L}^{{(i,1)}}}(z,{{z}_{1}}){{V}^{{(1)}}}({{z}_{1}}) + \sum\limits_{j = 1}^i {{{L}^{{(i,j)}}}} \times \hfill \\ \times \,\,(z,{{z}_{j}})\left( {{{W}^{{(j - 1)}}}({{z}_{j}}) - {{W}^{{(j)}}}({{z}_{j}})} \right) + {{W}^{{(i)}}}(z), \hfill \\ \end{gathered} $В конечной точке системы слоeв согласно (4) получим
Формула (5) связывает значения потенциала $\Delta {{p}^{{(i)}}}(z)$ и потока ${{J}^{{(i)}}}(z)$ в первой и последней точке системы слоев, что позволяет в общем случае сводить решение краевой задачи первого, второго или третьего типа при любом конечном числе слоев к решению системы двух линейных уравнений с двумя неизвестными, после чего рассчитывается КЛ от многослойной структуры.
Отметим, что для аналитического решения рассматриваемой задачи диффузии ННЗ в многослойной среде необходимо знать частное решение уравнения (1). В случае, если частное решение найти не удается или оно имеет очень сложный вид, можно по данному алгоритму получить приближенное решение задачи (1), (2), аппроксимировав правую часть, например линейными функциями [11].
РЕЗУЛЬТАТЫ РАСЧЕТОВ
Некоторые возможности предлагаемого метода показаны на рис. 1–3. На рис. 1 представлены результаты расчeтов по глубине относительных величин плотности потерь энергии электронами пучка, рассчитанные для однородных монокристаллических ${\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}$ (кривая 1) и CdTe (кривая 2) при энергии электронов пучка 20 кэВ. На рис. 2 представлены распределения ННЗ, генерированных электронным пучком в двухслойной полупроводниковой структуре ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}$ толщиной 0.4 мкм (0.1 мкм – ${\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}$ и 0.3 мкм – CdTe) для различных энергий электронов пучка: 5 (кривая 1), 10 (2), 15 (3), 20 (4), 25 (5) и 30 кэВ (6). Расчеты проведены для электрофизических параметров, характерных для твeрдого раствора кадмий-ртуть-теллур (КРТ). Результаты расчeтов аналитическим методом и численным методом конечных разностей практически совпадают и потому на рисунке не выделены. На рис. 3 представлены зависимости интенсивности монохроматической КЛ твердого раствора ${\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}$ толщиной 0.1 мкм двухслойной структуры ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}$ от энергии электронов пучка для различных коэффициентов поглощения в плeнке КРТ: 10 (кривая 2) и 104 см–1 (кривая 1).
Рис. 1.
Распределение по глубине относительных величин плотности потерь энергии электронами пучка, рассчитанные для однородных монокристаллических ${\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}$ (сплошная кривая) и CdTe (пунктирная кривая). Энергия электронов пучка 20 кэВ.
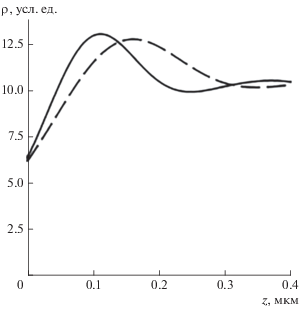
Рис. 2.
Распределения ННЗ, генерированных электронным пучком в двухслойной полупроводниковой структуре ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}$ толщиной 0.4 мкм (0.1 мкм – ${\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}$ и 0.3 мкм – CdTe) для различных энергий электронов пучка: 5 кэВ (кривая 1), 10 (2), 15 (3), 20 (4), 25 (5), 30 (6). Результаты расчетов аналитическим методом и численным методом практически совпадают и потому на рисунке отдельно не выделены.

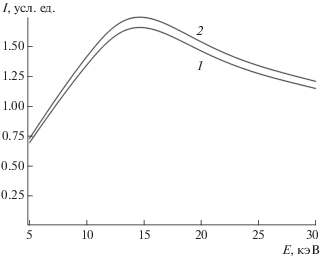
Рис. 3.
Зависимости интенсивности монохроматической КЛ твердого раствора ${\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}$ толщиной 0.1 мкм двухслойной структуры ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}$ от энергии Е электронов пучка для различных коэффициентов поглощения в пленке КРТ: 10 (кривая 2) и 104 см–1 (кривая 1).
ЗАКЛЮЧЕНИЕ
Описаны результаты изучения возможностей приложения аналитического матричного метода к моделированию КЛ, обусловленной широким электронным пучком в планарной многослойной полупроводниковой структуре с произвольным числом слоев. Предложенный матричный метод позволяет проводить расчеты распределений неравновесных неосновных носителей заряда и монохроматической КЛ с точностью, достаточной для практического использования в электронно-зондовых технологиях.
Исследования проведены при финансовой поддержке Российского фонда фундаментальных исследований (проект № 19-03-00271), а также РФФИ и правительства Калужской области (проект № 18-41-400001).
Список литературы
Степович М.А. Количественная катодолюминесцентная микроскопия прямозонных материалов полупроводниковой оптоэлектроники. Дис. … докт. физ.-мат. наук. М.: МГТУ им. Н.Э. Баумана, 2003. 351 с.
Bresse J.F. // Mater. Sci. Engin. 1996. V. B 24. № 1. P. 199.
Хохлов А.Г., Петров В.И., Снопова М.Г., Степо-вич М.А. // Поверхность. Рентген., синхротр. и нейтр. иссл. 2005. № 9. С. 64; Khokhlov A.G., Pet-rov V.I., Snopova M.G., Stepovich M.A. // J. Surf. Invest. X-ray, Synchrotron Neutron Tech. 2005. № 9. P. 64.
Snopova M.G., Khokhlov A.G., Mikheev N.N., Stepovich M.A. // Proc. SPIE. 2006. V. 6278. Art. № 627800.
Снопова М.Г., Михеев Н.Н., Петров В.И., Степович М.А. // Изв. РАН. Сер. физ. 2008. Т. 72. № 11. С. 1534; Snopova M.G., Mikheev N.N., Petrov V.I., Stepovich M.A // Bull. Russ. Acad. Sci. Phys. 2008. V. 72. № 11. P. 1451.
Carslaw H.S., Jaeger J.C. Conduction of heat in solids. Oxford: Oxford University Press, 1959. 517 p.
Bers L., Gelbart A. // Trans. Am. Math. Soc. 1944. V. 56. P. 67.
Гладышев Ю.А., Калманович В.В., Степович М.А. // Поверхность. Рент., синхротр. нейтр. иссл. 2017. № 10. С. 105; Gladyshev Yu.A., Kalmanovich V.V., and Stepovich M.A. // J. Surf. Invest. X-ray, Synchrotron Neutron Tech. 2017. V. 11. № 5. P. 1096.
Калманович В.В., Степович М.А. // Пробл. разраб. персп. микро- и наноэл. сист.-2018. Сб. тр. М.: ИППМ РАН, 2018. С. 194.
Гладышев Ю.А., Калманович В.В., Серегина Е.В., Степович М.А. // Вопр. атом. науки и тех. Яд-реакт. констр. 2018. № 3. С. 158.
Kalmanovich V.V., Seregina E.V., Stepovich M.A. // J. Phys. Conf. Ser. 2019. V. 1163. Art. № 012012.
Михеев Н.Н., Никоноров И.М., Петров В.И., Степович М.A. // Изв. АН СССР. Сер. физ. 1990. Т. 54. № 2. С. 274; Mikheev N.N., Nikonorov I.M., Petrov V.I., Stepovich M.A. // Bull. Acad. Sci. USSR. Phys. 1990. V. 54. № 2. P. 82.
Михеев Н.Н., Петров В.И., Степович М.А. // Изв. АН СССР. Сер. физ. 1991. Т. 55. № 8. С. 1474; Mikheev N.N., Petrov V.I., Stepovich M.A. // Bull. Acad. Sci. USSR. Phys. 1991. V. 55. № 8. P. 1.
Михеев Н.Н., Степович М.А. // Завод. лаб. диагн. матер. 1996. Т. 62. № 4. С. 20; Mikheev N.N., Stepovich M.А. // Indust. Lab. 1996. V. 62. № 4. P. 221.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


