Известия РАН. Серия физическая, 2020, T. 84, № 7, стр. 1004-1009
Определение коэффициента температуропроводности прозрачных материалов модифицированным методом лазерной вспышки
Ю. И. Головин 1, 2, *, А. И. Тюрин 1, Д. Ю. Головин 1, А. А. Самодуров 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Тамбовский государственный университет имени Г.Р. Державина”
Тамбов, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”
Москва, Россия
* E-mail: nano@tsutmb.ru
Поступила в редакцию 18.02.2020
После доработки 16.03.2020
Принята к публикации 27.03.2020
Аннотация
Описан новый термографический экспресс-метод определения коэффициента температуропроводности прозрачных материалов и оптических компонентов, а также результаты его тестирования на стеклах и полимерных материалах. Алгоритм извлечения величины коэффициента температуропроводности из первичных данных исключает необходимость определения абсолютных температур и поглощенной энергии падающего потока излучения и обеспечивает случайную погрешность менее 2–3%.
ВВЕДЕНИЕ
Кинетические теплофизические характеристики (ТФХ) прозрачных материалов (коэффициенты температуропроводности а и теплопроводности λ) определяют прочность и стойкость оптических элементов под воздействием интенсивных световых потоков [1, 2]. Для определения ТФХ материалов разработано множество различных методов и специальное оборудование. Методы можно разделить на два класса – стационарные и нестационарные [3–6].
Исторически более ранние cтационарные методы до сих пор широко применяются на практике, однако они имеют ряд недостатков, обусловленных тем, что распределение тепловых потоков должно в достаточной степени приблизиться к планируемой асимптотике стационарного распределения температуры без значимых неконтролируемых утечек тепла из измерительной ячейки. Эти методы требуют изготовления образцов определенных размеров и формы из тестируемых материалов и большого времени для достижения стационарного режима в них, что сильно затрудняет соблюдение принятых в расчетной схеме граничных условий на свободных поверхностях исследуемого образца и увеличивает влияние различных дрейфов на точность измерений. Установки такого типа требуют специальных мер теплоизоляции и термостабилизации образца, нагревателя, холодильника и измерительного тракта, обеспечения малых тепловых сопротивлений между нагревателем, образцом, холодильником и датчиками температуры. Ввиду этих обстоятельств установки для реализации стационарных методов громоздки и имеют ограниченный диапазон измеряемой теплопроводности.
Нестационарные методы более разнообразны. Они используют различные временные зависимости интенсивности подводимого теплового потока – обычно это дельта-функция (импульс Дирака), ступенчатое или периодическое возбуждение [3–6]. В негармонических нестационарных подходах в настоящее время наиболее часто используют метод лазерной вспышки (МЛВ), предложенный еще в 1961 г. У. Паркером с соавторами [7], а также созданные впоследствии родственные методы активной динамической термографии [8–10].
Классический метод лазерной вспышки реализуют с помощью самостоятельно разработанного или коммерчески доступного лабораторного оборудования (см., например, [11, 12]), работающего в соответствии с международными стандартами [13, 14]. Стандартизованный МЛВ и соответствующий инструментарий имеют ряд несомненных достоинств – высокая точность и хорошая воспроизводимость результатов измерений, малая продолжительность тестирования (~1 с), возможность контроля состава газовой среды и температуры в интервале от –120 до 2800°C и др. Однако МЛВ обладает и рядом серьезных недостатков. Для исследования необходимо использовать только специально подготовленные образцы определенной формы (обычно это диск диаметром 12–25 мм и толщиной 1–3 мм). МЛВ требует дорогого оборудования и доступа с двух сторон к исследуемому образцу. В совокупности это не позволяет работать на массивных или не подготовленных специально образцах, а также готовых изделиях, находящихся в процессе эксплуатации или имеющих доступ только с одной стороны. Измерение ТФХ прозрачных материалов методами динамической термографии и МЛВ требует дополнительных мер по исключению влияния оптических свойств на тепловые характеристики [15]. Обычно это достигается равномерным зачернением или металлизацией лицевой поверхности образца, нагреваемой лазерным излучением.
Цель настоящей работы – разработка не нуждающегося в пробоподготовке универсального экспрессного способа определения коэффициента температуропроводности (КТП) a различных прозрачных материалов (полимеров и стекол) и изделий из них с помощью определенным образом организованного эксперимента, а также оригинальных алгоритмов и программного обеспечения.
МЕТОДЫ И МАТЕРИАЛЫ
В основе предлагаемого подхода лежит термография нестационарного температурного поля, индуцируемого источником локального нагрева. Регистрируемое тепловизионной камерой ИК изображение обрабатывали с помощью оригинальных алгоритмов и программного обеспечения. Тепловизоры успешно используют в различных приложениях [3–6, 8–10]. Они предоставляют ряд преимуществ при регистрации эволюции распределения температуры в изучаемом образце. В отличие от локальных датчиков температуры (термопар, термисторов и др.) при таком способе регистрации кроме очевидного достоинства – способности получать информацию бесконтактно и одновременно в большом количестве точек, существенно улучшается точность пространственной локализации получаемых данных и исключаются проблемы, связанные с тепловой инерцией датчика и привнесенными им добавочными теплоемкостью, теплоотводом и тепловым сопротивлением на его границе.
Вместе с тем, важно отметить, что в случае использования лазера в качестве источника энергии и тепловизора в качестве регистратора, точное измерение абсолютных температур объекта и тепловых потоков через него весьма затруднительно (из-за плохо известных оптических коэффициентов поглощения, отражения и испускания разнообразных контролируемых поверхностей и их вариаций от точки к точке). Однако предлагаемый подход и не нуждается в знании абсолютных температур (как, впрочем, и классический МЛВ), поскольку природа теплофизической характеристики “коэффициент температуропроводности” определяется лишь соотношением характерных размеров r и времени t при распространении теплового фронта от источника нагрева, что видно из физического смысла величины КТП a, ее размерности [м2/с] и определения безразмерного критерия подобия Фурье Fo = at/r2. Важно лишь, чтобы коэффициент, связывающий абсолютную температуру с откликом измерительной системы, был постоянным для всей области наблюдения (из подобных соображений исходят и в классическом МЛВ, где при известной толщине образца измеряемой величиной является время достижения половины максимального значения температуры тыльной стороны образца, а не сама температура).
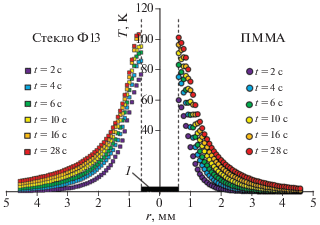
Предлагаемый подход основан на ступенчатом точечном нагреве участка поверхности образца лучом лазера, сфокусированным в пятно c гауссовым радиусом r0 = 0.1–0.3 мм, и одновременной регистрации формирующегося в результате такого нагрева динамического температурного поля на поверхности образца с помощью тепловизора (рис. 1). Последующая компьютерная обработка радиально симметричной картины изотерм по разработанным моделям и алгоритмам позволяет определять величину a.
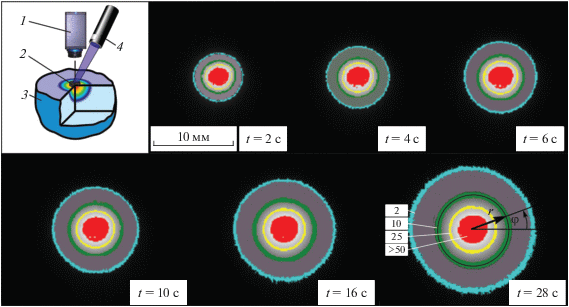
Рис. 1.
Термограмма для стекла Ф13. Изотермы показаны в виде колец 2 ± 0.25; 10 ± 1; 25 ± 1; >50 К. На врезке показана схема эксперимента и картина изотерм вблизи места нагрева. Обозначения: 1 – тепловизор, 2 – мишень, 3 – образец, 4 – лазер, r – расстояние от центра пятна нагрева, φ – угол усреднения.
Верификация описанного подхода определения а проведена на ряде материалов (полиметилметакрилат, ПММА; поликарбонат; оптические бесцветные стекла ТК8 и Ф13), значительно отличающихся как теплофизическими, так и оптическими свойствами. Все образцы имели вид массивных деталей диаметром >30 мм и высотой >25 мм.
В описанных ниже экспериментах точечный нагрев осуществляли ступенчатым импульсом сфокусированного лазерного пучка с одновременной регистрацией эволюции латеральной тепловой волны на поверхности образца с помощью тепловизора подобно [10]. Однако лазер создавал не короткую вспышку, как в классическом лазер-флэш методе и в его латеральных модификациях [10, 16–18], а работал непрерывно в течение всего процесса измерения, как в [19–23].
Это позволяло значительно уменьшить локальный перегрев в центре пятна нагрева, одновременно увеличив температуру во всей инспектируемой области, а также снизить требования к мощности лазера. Для увеличения поглощения энергии в пятне нагрева в ряде случаев на поверхность образца с помощью термопасты крепили непрозрачную мишень (диск из свинца диаметром 0.5 мм и толщиной 0.2 мм) или с помощью более мощного сфокусированного лазерного пучка создавали карбонизированную область диаметром 0.3–0.5 мм (для пластиков).
В качестве нагревателя был использован твердотельный лазер с диодной накачкой (лазерный модуль LSR445CP-FC-10W), регулируемой мощностью 1–10 Вт и длиной волны 445 нм. Цифровое ИК-изображение наружной поверхности получали с помощью тепловизора FLIR A35sc с наибольшей чувствительностью в диапазоне длин волн 7.5−13 мкм (матрица болометров на оксиде ванадия VOx 320 × 256 пикселей); угловым разрешением 2.78 мрад; порогом чувствительности ~0.05°С в диапазоне температур от −20 до 550°С; частотой выводимых и сохраняемых кадров 60 Гц. Получаемые кадры фильма (рис. 1) преобразовывали в двумерные карты распределения температуры. Для уменьшения влияния неоднородности оптических свойств поверхности образца из каждой такой карты попиксельно вычитали карту начального состояния до начала нагрева и в дальнейшем для обработки использовали величину T = Тh – Т0, где Тh – текущая температура в точке, T0 – начальная температура (до включения нагрева). Затем определяли положение центра симметрии изотерм и при фиксированных расстояниях r от него производили усреднение величины Т по углу φ (рис. 1) по нескольким десяткам пикселей, что сильно снижало шумы и помехи при измерениях. Как правило, для определения a принимали φ = = 360°. На рис. 2 показаны полученные описанным методом распределения T(r, t) в макрооднородных бездефектных образцах ПММА и стекле Ф13.
ТЕПЛОВАЯ МОДЕЛЬ И ОБРАБОТКА ПЕРВИЧНЫХ ДАННЫХ
Из соображений симметрии ясно, что точечный нагрев поверхности массивного однородного изотропного тела должен вызывать радиально-симметричное распространение сферического теплового фронта в полупространство исследуемого материала. Для ряда граничных условий известны точные решения уравнения Фурье. Так, в случае, когда тепловыделение происходит внутри полусферы радиусом R с заданным потоком тепла Q на ее границе, в адиабатическом приближении решение имеет вид [24]
(1)
$\begin{gathered} T(r,t) = ({Q \mathord{\left/ {\vphantom {Q {2\pi \lambda r}}} \right. \kern-0em} {2\pi \lambda r}})[{\text{erfc}}\left( {{{(r--R)} \mathord{\left/ {\vphantom {{(r--R)} 2}} \right. \kern-0em} 2}{{{\left( {at} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right)-- \\ - \,\,{\text{exp[}}{{(r--R)} \mathord{\left/ {\vphantom {{(r--R)} R}} \right. \kern-0em} R} - {{at} \mathord{\left/ {\vphantom {{at} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}]{\text{erfc[}}{{{\text{(}}r--R{\text{)}}} \mathord{\left/ {\vphantom {{{\text{(}}r--R{\text{)}}} {2{{{\left( {at} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {2{{{\left( {at} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} + \\ + \,\,{{{{{(at)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{{(at)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} R}} \right. \kern-0em} R}]], \\ \end{gathered} $(2)
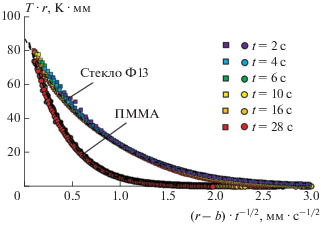
$T\left( {r,t} \right) = B{{r}^{{--1}}}{\text{erfc}}[{{\left( {r--b} \right)} \mathord{\left/ {\vphantom {{\left( {r--b} \right)} {2{{{(at)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {2{{{(at)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}],$Рис. 3.
Экспериментальные зависимости температуры Т от времени t и радиуса r в координатах Tr = = f[(r – b)t–1/2] (показаны точками) и результат расчета в рамках разработанной модели (показан пунктирной линией) для ПММА и стекла Ф13.
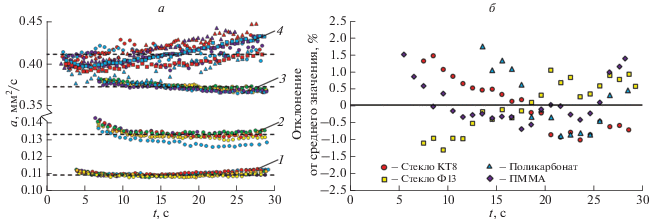
На рис. 4а приведены данные об индивидуальных значениях а в функции времени t, прошедшего от момента начала нагрева для нескольких тестов в каждом материале. Из этих данных следует, что в отличие от [10] предложенный подход и модель дают очень близкие значения а на большом интервале t, что позволяет в каждом тесте набирать большой статистический объем данных и многократно уменьшать погрешность измерения, вызванную различными случайными факторами, путем их усреднения. Некоторые различия в величине а, получаемые в разных тестах на одном материале при смещении области нагрева, могут быть обусловлены неоднородностью ТФХ в этом материале (наибольший эффект такого рода наблюдался в стекле Ф13, наименьший – в ПММА).
Рис. 4.
Временные зависимости: а) коэффициента температуропроводности а для ПММА – 1, поликарбоната – 2, стекла ТК8 – 3 и стекла Ф13 – 4 (кружочки – P = 1.2 Вт; треугольники – 1.6 Вт; квадратики – 2.5 Вт). Точками показаны экспериментальные данные, пунктирные линии – среднее значение величины а; б) отклонения величины а от среднего значения.
Из табл. 1 следует, что значения a, определенные предложенным нестационарным экспресс-методом, совпадают с табличными значениями a* [25, 26] (в отсутствие прямых табличных данных по а* ее величина вычислялась по формуле a* = λ/cрρ, где соответствующие значения λ, плотности ρ и удельной теплоемкости cр брали из таблиц).
Таблица 1.
Полученные и справочные значения а для исследованных материалов
| Материал | Измеренные и справочные значения а | Номер теста | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| ПММА | a, мм2/с | 0.1095 | 0.1103 | 0.1104 | 0.1094 | 0.1094 | 0.1102 | 0.1087 | 0.1096 | 0.1093 |
| δа, мм2/с | 0.0005 | 0.0008 | 0.0010 | 0.0007 | 0.0007 | 0.0007 | 0.0005 | 0.0010 | 0.0010 | |
| a9, мм2/с | 0.1096 ± 0.0008 | |||||||||
| а*, мм2/с | 0.08–0.12 | |||||||||
| Поликарбонат | a, мм2/с | 0.1304 | 0.1344 | 0.1335 | 0.1327 | 0.1359 | 0.1346 | 0.1346 | 0.1321 | 0.1334 |
| δа, мм2/с | 0.0013 | 0.0006 | 0.0010 | 0.0006 | 0.0010 | 0.0020 | 0.0008 | 0.0011 | 0.0010 | |
| a9, мм2/с | 0.1335 ± 0.0010 | |||||||||
| а*, мм2/с | 0.07–0.17 | |||||||||
| Стекло Ф13 | a, мм2/с | 0.4107 | 0.4071 | 0.4132 | 0.4088 | 0.4171 | 0.4091 | 0.4120 | 0.4129 | 0.4117 |
| δа, мм2/с | 0.0018 | 0.0028 | 0.0028 | 0.0035 | 0.0040 | 0.0031 | 0.0037 | 0.0018 | 0.0031 | |
| a9, мм2/с | 0.4114 ± 0.0030 | |||||||||
| а*, мм2/с | 0.41 | |||||||||
| Стекло ТК8 | a, мм2/с | 0.3706 | 0.3717 | 0.3743 | 0.3735 | 0.3733 | 0.3716 | 0.3758 | 0.3734 | 0.3742 |
| δа, мм2/с | 0.0024 | 0.0038 | 0.0027 | 0.0028 | 0.0019 | 0.0035 | 0.0024 | 0.0025 | 0.0019 | |
| a9, мм2/с | 0.3732 ± 0.0027 | |||||||||
| а*, мм2/с | 0.37 | |||||||||
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Как видно из рис. 4 и табл. 1, случайные погрешности измерений а предложенным методом не превышают 2–3%. Систематические погрешности оцениваются величиной такого же уровня. Последние обусловлены рядом причин, основными из которых являются погрешности масштабирования изображения и аберрации в оптике тепловизора, неадиабатичность нагрева, нарастающая по мере роста продолжительности эксперимента, зависимость ТФХ исследованных материалов от температуры (особенно – пластиков). Борьба с ними является задачей следующего этапа совершенствования методики измерений. Однако и без этих коррекций модель сферического теплового фронта успешно работает в достаточно широком диапазоне времен t и радиусов изотерм r. Снизу они ограничены необходимым временем и расстоянием от центра пятна нагрева, чтобы “забыть” о конкретных особенностях распределения энергии в нем. Ограничения сверху обусловлены падением сигнала и отношения сигнал/шум, а также ростом роли теплопотерь с нагретого участка поверхности.
Подчеркнем еще раз, что метод не требует знания точного абсолютного значения температур поверхности и тепловых потоков, поскольку они не входят в расчетные алгоритмы и формулы для вычисления a. Достаточно лишь допущения оптической однородности поверхности, а именно, постоянства коэффициента испускания. Максимальный нагрев в области тестирования зависел от плотности потока в пятне нагрева, его радиуса и длительности процедуры измерения. Ни в каких опытах он не превышал нескольких десятков °С, а в области измерения – единиц °С, что позволяет считать метод неразрушающим и относить полученные значения a к температуре окружающей среды.
ЗАКЛЮЧЕНИЕ
Сформулируем основные особенности и преимущества предложенного подхода, подтвержденные полученными результатами:
1. Способ характеризуется большим интервалом времени, в котором индивидуальные измерения а (в количестве многих тысяч) демонстрируют очень низкое рассеяние (<1%). Это – прямое следствие того, что каждое индивидуальное измерение производилось на основе покадрового учета радиального распределения температуры. Последнее извлекали путем обработки каждого отдельного кадра фильма с усреднением температур всех пикселей изображения, находящихся в узкой кольцевой области при заданном среднем радиусе. Такое двойное усреднение обеспечивало богатую статистику и, как следствие, высокую точность измерения а;
2. Малая продолжительность измерения τ; для протестированных материалов с умеренными значениями величины a ~ 1–15 мм2/с она составляла τ = 1–10 с;
3. Как следствие, малая продолжительность измерения τ приводит к снижению погрешностей, связанных с конвективными утечками тепла, влиянием материала и конструктивных элементов, окружающих зону нагрева, а также другими случайными причинами;
4. Низкие требования к геометрии образца и пробоподготовке – минимально необходимый размер образца – 5–10 мм в любом направлении от точки нагрева, а также макроскопически плоская поверхность в этой области;
5. Слабое или почти полное отсутствие влияние оптических свойств поверхности на результаты измерений;
6. Хорошая воспроизводимость результатов со среднеквадратичным отклонением в единицы процентов, обусловленная малостью свободной поверхности, краткостью процедуры измерений и, как следствие, слабой зависимостью результатов от влияния окружающей среды и полным отсутствием таковой от объемов материала за пределами зоны измерения;
7. Возможность проведения измерений при одностороннем доступе к объекту тестирования.
Работа поддержана РНФ (проект № 15-19-00181 – проведение эксперимента и обработка данных), РФФИ (проект № 17-48-680817 – разработка аналитических и компьютерных моделей) и Минобрнауки РФ (проект № 16.2100.2017/4.6 – изготовление и отладка оригинального пилотного прибора). Экспериментальные результаты были получены на оборудовании ЦКП ТГУ им. Г.Р. Державина.
Список литературы
Осико В.В. Лазерные материалы. М.: Наука, 2002. 493 с.
Попов П.А., Дукельский К.В., Миронов И.А. и др. // ДАН. 2007. Т. 412. № 2. С.185.
Лыков А.В. Методы определения теплопроводности и температуропроводности. М.: Энергия, 1973. 336 с.
Вавилов В.П. Инфракрасная термография и тепловой контроль. М.: Спектр, 2013. 542 с.
Hammerschmidt U., Hameury J., Strnad R. et al. // Int. J. Thermophys. 2015. V. 36. P. 1530.
Yüksel N. // In: Insulation materials in context of sustainability. Ch. 6. London: InTech, 2016. P. 113.
Parker W.J., Jenkins R.J., Butler C.P., Abbot G.L. // J. Appl. Phys. 1961. V. 32. P. 1679.
Скворцов Л.А. Основы фототермической радиометрии и лазерной термографии. М.: Техносфера, 2017. 220 с.
Okamoto Y., Watanabe S., Ogata K. et al. // Jap. J. Appl. Phys. 2017. V. 56. Art. № 056601.
Kruczek T., Adamczyk W.P., Bialecki R.A. // Int. J. Thermophys. 2013. V. 34. P. 467.
www.netzsch.com.
www.tainstruments.com/wp-content/uploads/ BROCH_ Light_Flash_2017.pdf
ISO 22007-4 (2017). Plastics. Determination of thermal conductivity and thermal diffusivity. Part 4. Laser flash method.
ASTM E1461-13. Standard test method for thermal diffusivity by the flash method.
Salazar A., Mendioroz A., Apiñaniz E. et al. // Meas. Sci. Technol. 2014. V. 25. № 3. Art. № 035604.
Dong H., Zheng B., Chen F. // Infrared Phys. Technol. 2015. V. 73. P. 130.
Genna S., Ucciardello N. // Opt. Laser Technol. 2019. V. 113. P. 338.
Bedoya A., González J., Rodríguez J. et al. // Measurement. 2019. V. 134. P. 519.
Golovin Yu.I., Turin A.I., Golovin D.Yu., Samodurov A.A. // Inorg. Materials. 2019. V. 55. № 15. P. 7.
Головин Ю.И., Тюрин А.И., Головин Д.Ю., Самодуров А.А. // Завод. лаб. Диагн. матер. 2018. Т. 84. № 6. С. 23.
Головин Д.Ю., Тюрин А.И., Самодуров А.А. и др. // Изв. вузов. Физ. 2019. № 6. С. 159.
Golovin D.Y., Divin A.G., Samodurov A.A. et al. // In: Contemporary issues in non-destructive testing and evaluation. London: In Tech, 2019. P. 1.
Palumbo D., Cavallo P., Galietti U. // NDT E Int. 2019. V. 102. P. 254.
Carslaw H.C., Jaeger J.C. Conduction of heat in solids. Oxford: Oxford Univ. Press, 1959. 510 p.
ГОСТ 13659-78. Стекло оптическое бесцветное. Физико-химические характеристики. Основные параметры.
Новиченок Л.Н., Шульман Э.П. Теплофизические свойства полимеров. Минск: Наука и техника, 1971. 120 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая