Известия РАН. Серия физическая, 2020, T. 84, № 7, стр. 1040-1043
Исследование объемной и зернограничной диффузии олова в сплавах медь–олово
В. П. Никулкина 1, *, Б. С. Бокштейн 1
1 Федеральное государственное автономное образовательное учреждение высшего образования
“Национальный исследовательский технологический университет “МИСиС”
Москва, Россия
* E-mail: nikulkinavp@gmail.com
Поступила в редакцию 18.02.2020
После доработки 16.03.2020
Принята к публикации 27.03.2020
Аннотация
Методом микрорентгеноспектрального анализа получены концентрационные кривые и рассчитаны коэффициенты объемной и зернограничной диффузии в твердых растворах системы медь–олово при концентрации олова менее 13.9 мас. % в интервале температур от 500 до 650°С. Предложено качественное объяснение полученных результатов.
ВВЕДЕНИЕ
Система медь–олово широко используется в электротехнике, поскольку она обладает высокой теплопроводностью, имеет удовлетворительные механические (антифрикционные) свойства, хорошее сопротивление коррозии [1] и является одним из основных элементов припоев [2]. Имеется ряд исследований, посвященных диффузионным процессам в системе медь–олово [3–15]. Следует отметить, что все они ограничиваются случаем объемной диффузией при сравнительно высоких (выше 700°С) температурах и сопутствующими ей процессами, такими как рост промежуточных фаз. Нет данных о зернограничной диффузии олова в меди и сплавах на основе меди, хотя важная роль зернограничной диффузии очевидна, особенно благодаря миниатюризации электронных устройств и широкому использованию металлической фольги в таких системах.
Цель настоящей работы – измерение параметров объемной и зернограничной диффузии в широком интервале концентраций олова, при умеренно высоких температурах (от 500 до 650°С).
МЕТОД ИССЛЕДОВАНИЯ
Диффузию олова исследовали в α-твердом растворе на основе Cu, существующем в широком интервале концентраций (до 9.1 ат. %) Sn при 586°С. Растворимость олова в этих растворах практически постоянна в диапазоне температур от 350 до 798°С.
Диффузионные пары были изготовлены из чистой меди и двухкомпонентного сплава с концентрацией, соответствующей растворимости олова в меди при температуре перитектической реакции (798°С). Поэтому были изготовлены сплавы с содержанием олова 8 ат. % в твердом растворе. В этом случае в диффузию не вмешивались процессы фазообразования.
Сплав готовили прямым сплавлением меди с оловом при температуре 1100°C в атмосфере аргона с добавлением водорода. Состав сплава контролировали атомно-эмиссионным методом с индуктивно-связанной плазмой (АЭС-ИСП). Анализ показал, что содержание олова в различных слитках колебалось в пределах 8–8.3 ат. %.
Из сплава и чистой меди вырезали пластины толщиной около 1 мм, поверхность нарезанных пластин шлифовали и полировали с использованием алмазной суспензии до зеркального блеска, после чего пластину Cu–Sn зажимали между двумя пластинами чистой меди в графитовой струбцине. Полученный трехслойный образец предварительно отжигали в инертной атмосфере при температуре 800°C в течение одного часа и проверяли надежность соединения.
Диффузионный отжиг образцов проводили в вакуумированных кварцевых ампулах при давлении 3 ∙ 10–3 Па в интервале температур от 500 до 650°C в течение длительного времени. В табл. 1 представлены условия диффузионных исследований и количество проанализированных профилей с каждого образца. Для исследования образцы разрезали вдоль направления диффузионного потока. После отжига и резки образцы подготавливали к исследованию структуры с помощью низковакуумного растрового электронного микроскопа.
Таблица 1.
Условия диффузионных исследований
| № п/п | Количество профилей | Диффузионные режимы | |
|---|---|---|---|
| температура, °C | время отжига, часы | ||
| 1 | 7 | 500 | 100 |
| 2 | 14 | 560 | 200 |
| 3 | 20 | 580 | 200 |
| 4 | 6 | 600 | 200 |
| 5 | 4 | 650 | 50 |
Рабочее напряжение для элементного анализа составляло 15 кВ. Для определения коэффициентов диффузии исследовали элементный состав в точках, расположенных перпендикулярно исходной поверхности раздела медь/сплав по границам зерен и вдали от них.
ОБЪЕМНАЯ ДИФФУЗИЯ
На рис. 1 показан концентрационный профиль. Обращает на себя внимание асимметричный вид концентрационной кривой. Такая асимметрия, как правило, связана с зависимостью коэффициента диффузии от концентрации. Из асимметрии профиля (сравните область D1 с концентрацией олово от 6 до 8 ат. % с областью D2, в которой концентрация олова меняется от 2 до 0 ат. %) следует, что коэффициент диффузии повышается с увеличением концентрации олова и в сплаве, и вблизи линии растворимости, где его значение больше, чем вблизи чистой меди.
Для определения коэффициентов диффузии был использован метод Грубе [16], в котором концентрационный профиль разбивается на малые отрезки, для которых принимается D = const, и используется решение второго уравнения Фика для двух полубесконечных пластин [17]:
(1)
$C = \frac{{{{c}_{0}}}}{2}{\text{erfc}}\left( {\frac{{y - {{y}_{0}}}}{{2{{{(Dt)}}^{{0.5}}}}}} \right),$со следующими начальными и граничными условиями
(2)
$\begin{gathered} c(--\infty ,\,t) = {{c}_{0}};\,\,с(\infty ,t) = 0c(y,0) = {{С}_{0}}y < 0; \\ c\left( {y,0} \right) = 0y > 0. \\ \end{gathered} $Это уравнение использовали раздельно для левой и правой частей профиля, задавая у0 как условную поверхность раздела между высокооловянной частью, которая хорошо описывается коэффициентом диффузии D1, и низкооловянной частью, описываемой коэффициентом D2. Таким образом, определяли коэффициенты диффузии для областей, богатой оловом (6–8 ат. %) D1 и бедной оловом (менее 2 ат. %) D2.
Результаты приведены в табл. 2 в сравнении с литературными данными о диффузии олова в чистой меди. Во всех случаях значение D2 близко к литературным данным, а отношение D1/D2 составляет несколько единиц.
Таблица 2.
Значения коэффициентов объемной диффузии (D ∙ 1016, м2/с) Sn в α-твердом растворе системы Cu–Sn
| Т, °C | D, 1016 м2/с | |||
|---|---|---|---|---|
| Согласно [8] | ${{\bar {D}}_{1}}$ | ${{\bar {D}}_{2}}$ | ${{{{{\bar {D}}}_{1}}} \mathord{\left/ {\vphantom {{{{{\bar {D}}}_{1}}} {{{{\bar {D}}}_{2}}}}} \right. \kern-0em} {{{{\bar {D}}}_{2}}}}$ | |
| 500 | 0.17 | 0.35 | 0.16 | 2.2 |
| 580 | 2.7 | 7.8 | 3.5 | 2.2 |
| 650 | 20 | 44 | 18 | 2.4 |
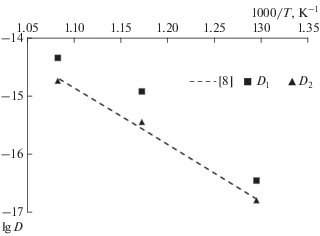
На рис. 2 представлена аррениусовская зависимость коэффициентов объемной диффузии в виде:
(3)
${{D}_{1}} = 5.6 \times {{10}^{{ - 4}}}\exp \left( {\frac{{ - 194\,{{{\text{кДж}}} \mathord{\left/ {\vphantom {{{\text{кДж}}} {{\text{моль}}}}} \right. \kern-0em} {{\text{моль}}}}}}{{RT}}} \right)\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {\text{с}}}} \right. \kern-0em} {\text{с}}},$(4)
${{D}_{2}} = 0.92 \times {{10}^{{ - 4}}}\exp \left( {\frac{{ - 188\,{{{\text{кДж}}} \mathord{\left/ {\vphantom {{{\text{кДж}}} {{\text{моль}}}}} \right. \kern-0em} {{\text{моль}}}}}}{{RT}}} \right)\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}.$И первое, и, тем более, второе значение энергии активации практически полностью совпадают с результатами изотопных измерений диффузии олова в чистой меди (187 кДж/моль).
Отметим, что коэффициент D1 соответствует диффузии в твердом растворе при температуре значительно ниже, чем температура плавления чистой меди, поэтому следовало бы ожидать уменьшения энергии активации по сравнению с энергией активации диффузии олова в чистой меди, однако наши результаты показывают, что этого не происходит. Полученный результат может быть объяснен следующим образом.
В соответствии с теорией Даркена [18] коэффициент диффузии в концентрированном (неидеальном) растворе (D) связан с коэффициентом диффузии в разбавленном растворе (D*) соотношением
(5)
$D = D{\kern 1pt} *({{1 + \partial \ln \gamma } \mathord{\left/ {\vphantom {{1 + \partial \ln \gamma } {\partial \ln c}}} \right. \kern-0em} {\partial \ln c}}),$Значения коэффициента активности как функции концентрации при температуре 1000 К были взяты из работы [19]. Соответственно, можно рассчитать термодинамическую поправку.
В α-твердом растворе Cu–Sn коэффициент активности Sn растет с ростом концентрации и, таким образом, D > D*. Оценка показывает, что второй член в уравнении Даркена около 1, что и дает удвоение коэффициента диффузии.
Из сравнения данных, полученных в работах [19] для 1000 и 723 К, видно, что коэффициент активности зависит от температуры, однако термодинамическая поправка остается практически постоянной. Поэтому коэффициент диффузии меняется, а энергия активации – нет.
ЗЕРНОГРАНИЧНАЯ ДИФФУЗИЯ
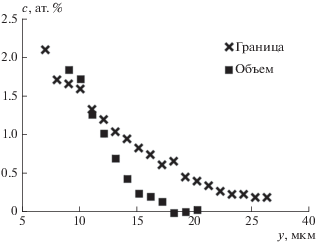
Зернограничную диффузию (ЗГД) изучали в тех же температурных и временных интервалах. Для этого шлифы предварительно травили в 40% водном растворе аммиака и 1–2% водном растворе 10% пероксида водорода [13] для выявления границ зерен, выходящих на поверхность раздела медь/сплав. На рис. 3 представлена микрофотография границы зерна.
Далее сравнивали концентрационные профили вдоль границ зерен: в непосредственной близости от границы и вдали от нее. Таким образом, можно выявить опережающую зернограничную диффузию. Важно отметить, что ускоренная ЗГД была обнаружена только у части исследованных границ. Дальнейшие результаты представлены для тех границ, в которых она была обнаружена.
Диффузионный отжиг проводили при 3 температурах: 560 (200 ч), 600 (200 ч) и 650°C (100 ч). Эти режимы дают объемную диффузию около 10 мкм, так что диффузионные потоки из соседних зерен не пересекаются, и было возможно исследовать диффузию вдоль каждой отдельной границы зерна.
Обработку результатов вели в рамках решения Фишера–Гиббса [20, 21] (модель опережающей диффузии с оттоком вещества с границы в объем), в котором учитывается сегрегация – обогащение границ зерен примесью по сравнению с объемом
где L – характерная длина фишеровской модели, s – коэффициент обогащения границы, δ – ширина границы, Db – коэффициент зернограничной диффузии, D – объемной диффузии и t – время.Расчет проводили для области с малой концентрацией олова. Такой выбор позволяет исключить осложнения, связанные с неидеальностью растворов.
Типичный концентрационный профиль приведен на рис. 4, а значения тройного произведения зернограничной диффузии P = sδDb – в табл. 3. Для перехода от Р к Db принимали δ = 0.5 нм и s = 20 [22], а при расчете L значение D – из ранее полученных экспериментальных измерений. В соответствии с уравнением (7) зависимость L от температуры определяется как P/D0.5 или как разница между $E_{b}^{{eff}}$ и E/2. Обычно оба значения близки (в наших экспериментах соотношение составляет 0.96), следовательно, L слабо зависит от температуры.
Таблица 3.
Средние значения L и P для разных температур
| T, °C | L, мкм | P, 10–21 м3 /с | D, 10–12 м3 /с |
|---|---|---|---|
| 560 | 23 | 3.9 | 0.79 |
| 600 | 29.7 | 9.5 | 1.9 |
| 650 | 19.5 | 18.1 | 3.6 |
Согласно уравнению Аррениуса:
(8)
$P = {{P}_{0}}\exp ({{--E{{b}^{{eff}}}} \mathord{\left/ {\vphantom {{--E{{b}^{{eff}}}} {RT}}} \right. \kern-0em} {RT}}).$Оценка эффективной энергии активации зернограничной диффузии, включающей в себя энергию сегрегации, дала $E_{b}^{{eff}}$ = 87.4 кДж/моль, что равно 0.48 от энергии активации объемной диффузии Sn в меди (187.6 кДж/моль). Предэкспоненциальный коэффициент P0 в уравнении Аррениуса составляет величину порядка 10–13 м3 ∙ с–1.
Для объяснения эффекта отсутствия опережающей диффузии для некоторых границ была рассчитана адсорбция на этих границах. Она оказалась близка к насыщению. Таким образом, градиент концентрации в указанных границах очень мал, что и приводит к отсутствию опережающей диффузии.
ЗАКЛЮЧЕНИЕ
Методом микрорентгеноспектрального анализа получены концентрационные профили и рассчитаны коэффициенты диффузии олова в твердом растворе системы Cu–Sn с концентрацией олова до 8% ат. в интервале температур от 500 до 650°C. Показано, что коэффициент диффузии олова в твердом растворе увеличивается по сравнению с диффузией олова в чистой меди. Получены экспериментальные значения тройного произведения P = sδDb для зернограничной диффузии олова в системе Cu–Sn в интервале температур 560–650°C. Эффективная энергия активации диффузии Sn в границах зерен в разбавленном твердом растворе на основе меди, рассчитанная по температурной зависимости тройного произведения, равна 874 кДж/моль. Отношение эффективной энергии активации к объемному значению равно 0.48.
Список литературы
Костржицкий А.И., Гусарева О.Ф. // Изв. АН СССР. Металлы. 1987. № 1. С. 169.
Wang J., Leinbach C., Liu H.S. et al. // CALPHAD. 2009. V. 33. P. 704.
Minho O., Vakanas G., Moelans N. et al. // Microelect. Engin. 2014. V. 120. P. 133.
Baheti V.A., Kashuap S., Kumar P. et al. // Alloys Compounds. 2017. V. 727. P. 832.
Labie R., Ruythooren W., VanHumbeeck J. // Intermetallics. 2007. V. 15. P. 396.
Chao B., Chae S.-H., Zhang X. et al. // Acta Mater. 2007. V. 55. P. 2805.
Gorbachev V.A., Klotsman S.M., Rabovskiy Y.A. et al. // Phys. Met. Metallogr. 1973. V. 35. P. 226.
Фогельсон Р.Л., Угай Я.А., Акимова И.А. // Физ. мет. и металловед. 1974. Т. 37. № 5. С. 201; Fogelson R.L., Ugay Y.A., Akimova I.A. // Phys. Met. Metallogr. 1974. № 37. № 5. Р. 1107.
Oikawa H., Hosoi A. // Scr. Met. 1975. V. 9. P. 82.
Hoshino K., Iijima A.Y., Hirano K.I. // Tr. Jap. Inst. Metals. 1980. V. 21. № 10. P. 674.
Mossi A. // Scr. Met. 1975. V. 9. P. 823.
Santra S., Paul A. // Phil. Mag. Lett. 2012. V. 92. № 8. P. 1.
Onishi M., Fujibuchi M. // Tr. Jap. Inst. Merals. 1975. V. 16. P. 539.
Paul A., Ghoshi C., Boetinger W.J. // Met. Mat. Trans. A. 2011. V. 42. P. 952.
Kumar S., Handwerker C., Dayamanda M., Phase J. // Equilib. Diffus. 2011. V. 32. № 4. P. 309.
Grube G., Jedele A. // Zt. Elektrochem. 1932. V. 38. P. 799.
Crank J. Mathematics of diffusion. Oxford, 1956.
Darken L. // Trans. AIME. 1948. V. 175. P. 184.
Predel B., Schallner U. // Mater. Sci. Engin. 1972. V. 10. P. 24.
Fisher J. C. // J. Appl. Phys. 1951. V. 22. P. 74.
Gibbs G.B. // Phys. Stat. Sol. 1966. V. 16. P. 27.
Nikulkina V.P., Rodin A.O., Bokstein B.S. // Mater. Lett. 2019. V. 257. Art. № 126525.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая