1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 7, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 7, стр. 1014-1019

Моделирование тепловых полей в аморфных сплавах при импульсной обработке эксимерным лазером

И. Е. Пермякова *

Федеральное государственное унитарное предприятие “Центральный научно-исследовательский институт черной металлургии имени И.П. Бардина”
Москва, Россия

* E-mail: inga_perm@mail.ru

Поступила в редакцию 18.02.2020
После доработки 16.03.2020
Принята к публикации 27.03.2020

Полный текст (PDF)

Аннотация

Проведено численное моделирование тепловых полей в ленточных аморфных сплавах систем Co–Fe–Cr–Si–B, Fe–Ni–B, Ti–Ni–Cu при импульсном лазерном УФ-облучении для оптимизации технологических режимов лазерной обработки с целью создания новых композиционных материалов с управляемым комплексом свойств.

ВВЕДЕНИЕ

В настоящее время лазерная обработка является весьма востребованной и перспективной технологией модификации структуры и свойств материалов [1]. В частности, лазерное облучение активно используется применительно к аморфным сплавам (АС), обладающим уникальным комплексом физико-механических характеристик, которые во многом превосходят свойства их кристаллических аналогов [2–5]. Для практического применения необходимо понимать механизмы кристаллизации АС, чтобы иметь возможность предотвращать или регулировать ее, т.к. именно стабильность по отношению к кристаллизации и определяет пределы эффективного использования АС. Аморфное состояние весьма чувствительно к вариациям температуры. На начальных стадиях нагрева в АС происходят процессы структурной релаксации, а при высоких температурах – протекают процессы кристаллизация. С другой стороны, контролируемую кристаллизацию можно использовать для построения структур, которые нельзя получить из жидкого или кристаллического состояний.

В результате лазерной обработки можно:

1) повышать термическую стабильность АС, смещая интервал кристаллизации в сторону более высоких температур;

2) изменять порядок фазообразования и тип кристаллизации;

3) формировать двухслойные аморфно-кристаллические структуры (композиты);

4) влиять на доменную структуру и, тем самым, снижать магнитные потери;

5) повышать прочность и твердость АС.

Для того чтобы гарантировано получить требуемые свойства и структурные состояния в АС при лазерной обработке, необходимо иметь целостное представление о взаимодействии лазерного излучения (ЛИ) с исследуемым материалом, изучить влияние режимов облучения и его параметров на отклик свойств и превращения в структуре.

Действие ЛИ на непрозрачные среды (металлы, сплавы) удовлетворительно можно описать тепловой моделью. Стадия нагрева является основной при исследованиях, а также при анализе технологических процессов, происходящих без разрушения материала.

Имеющиеся в распоряжение экспериментальные методы зачастую не позволяют непосредственно следить за распределением теплового поля в процессе лазерной обработки и оценить градиент температур, влияющий на ход структурообразования. По этой причине, а также для выбора оптимальных режимов лазера для контролируемого микро- и наноструктурирования АС с учетом их химического состава, исходных теплофизических свойств и качества поверхности, возникает необходимость предварительно провести компьютерное моделирование в среде Mathcad характеристик теплового поля при лазерном нагреве АС.

МАТЕРИАЛЫ И МЕТОДИКА РАСЧЕТОВ

При расчете для ввода параметров лазерной обработки и теплофизических характеристик использовали следующие данные:

– в качестве объектов исследований выбраны образцы быстрозакаленных лент АС Co70.5Fe0.5Сr4Si7B18, Fe50Ni33B17, Ti50Ni25Cu25 размером 1 × 1 см, толщиной 30 мкм, полученные методом спиннингования.

– облучение АС проводилось эксимерным ультрафиолетовым KrF-лазером (Excimer laser CL-7100) с длиной волны λ = 248 нм, длительностью импульса τ = 20 нс. Количество импульсов n варьировалось от 1 до 1000; энергия импульса Ei составляла 150 мДж; плотность энергии W – 0.3 Дж ∙ см–2; частота следования задавалась 2 Гц, радиус пятна Rs = 4.2 мм.

Длительность импульсов наносекундного ЛИ больше времени электрон-фононной релаксации, которое для различных материалов составляет несколько единиц или десятки пикосекунд. В связи с этим тепловые процессы начинают происходить уже во время воздействия лазерного импульса на материал, тем самым приводя к изменению его поверхности и свойств.

Поглощение ЛИ твердым телом эквивалентно появлению источника тепла внутри или на поверхности материала. Его реакцию на действие источника можно найти, решая трехмерное уравнение теплопроводности:

$\begin{gathered} \rho С\frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {k\frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {k\frac{{\partial T}}{{\partial y}}} \right) + \\ + \,\,\frac{\partial }{{\partial z}}\left( {k\frac{{\partial T}}{{\partial z}}} \right) + B\left( {x,y,z,t} \right), \\ \end{gathered} $
где ρ – плотность, k – теплопроводность, С – удельная теплоемкость материала, T – температура, B – функция распределения источников, x, y, z – декартова система координат, связанная с облученным телом, t – время [6].

Для выбора расчетной модели проведена теплофизическая оценка на основе анализа исходных данных [7]. Определена толщина h прогретого слоя, т.е. зоны термического влияния, на которую распространяется нагрев за 1 импульс, по приближенной формуле:

(2)
$h = 2\sqrt {\frac{{a\tau }}{\pi }} ,$
где a – температуропроводность АС, τ – длительностью импульса. Для АС Co70.5Fe0.5Сr4Si7B18 эта толщина составляет 0.75 мкм, для Fe50Ni33B17 – 0.76 мкм и для Ti50Ni25Cu25 – 0.49 мкм соответственно. Поскольку расстояние, на которое распространяется тепловой фронт по поверхности или в глубь материала за время действия ЛИ, значительно меньше радиуса фокального пятна и толщины ленты АС (h $ \ll $ Rs), в этом случае реализуется тепловая модель полубесконечного тела. Распределение интенсивности ЛИ по Гауссу позволяет, используя цилиндрическую симметрию источника ЛИ, получить точное решение тепловой двумерной задачи.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

В результате воздействия ЛИ на поверхность АС в них происходят структурные изменения. Особенности этих изменений обусловлены характеристиками возникающего температурного поля, такими как максимально достигнутые температура и скорости нагрева/охлаждения, распределение их по глубине зоны лазерного воздействия и т.д.

Для приближенного вычисления максимальной температуры нагрева поверхности при одном импульсе в центре облученной области в виде круга радиусом Rs (с учетом условия импульсного режима Rs $ \gg $ $\sqrt {а\tau } $) использовали уравнение:

(3)
${{T}_{{max}}} = {{T}_{0}} + 2qA\frac{{\sqrt {a\tau } }}{{k\sqrt \pi }},$
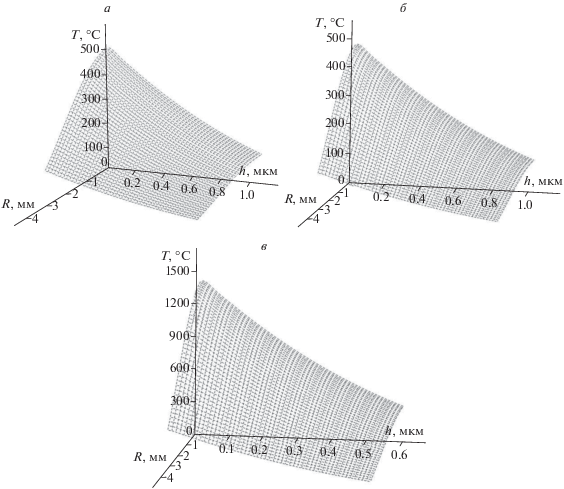
где T0 – начальная температура образца, q – плотность мощности ЛИ, A – коэффициент поверхностного поглощения ЛИ АС [8]. Результаты расчетов Tmax приведены в табл. 1 в сопоставлении с их температурами кристаллизации, определенными методами ДСК и РСА.

Таблица 1.  

Расчетные температуры максимального нагрева при одном лазерном импульсе и экспериментально установленные в работах [9–12] температуры кристаллизации АС

АС Tmax, °С Tcrys,°С
Co70.5Fe0.5Сr4Si7B18 505 530
Fe50Ni33B17 489 410
Ti50Ni25Cu25 1430 450

В рамках работы для АС произведен численный расчет распределения температуры по толщине h и радиусу пятна Rs при малых дозах облучения (рис. 1). Видно, что температура в облученной зоне лежит в диапазоне от 100 до 500°С (рис. 1а), что соответствует протеканию интенсивных процессов структурной релаксации в АС Co70.5Fe0.5Сr4Si7B18. В АС Fe50Ni33B17 лазерный отжиг даже небольшим числом импульсов будет инициировать процесс кристаллизации, поскольку Tmax несколько превышает Tcrys (рис. 1б, табл. 1). В случае АС Ti50Ni25Cu25 компьютерное моделирование дает более драматичный прогноз – облучением малыми дозами ЛИ достигаются плавильные температуры (рис. 1в).

Рис. 1.

Температурные поля в АС при 20 импульсах: Co70.5Fe0.5Сr4Si7B18 (а), Fe50Ni33B17 (б), Ti50Ni25Cu25 (в).

В ходе расчетов температурного поля при больших дозах облучения (большим числом импульсов n) следует учитывать следующее: лазер, работающий в импульсном режиме, генерирует серию импульсов длительностью τ при частоте следования f; после окончания очередного импульса материал начинает остывать, и, если выполняется условие

(4)
$f < \frac{a}{{30{{r}^{2}}}},$

то накопление тепла от импульса к импульсу не происходит [8]. В нашем случае условие (4) при f = 2 Гц не выполняется. Таким образом, нельзя полагать, что результат расчета температуры зависит лишь от энергетических параметров отдельного импульса. При облучении исследуемого АС постепенно идет накопление тепла от импульса к импульсу и проникновение нагрева вглубь.

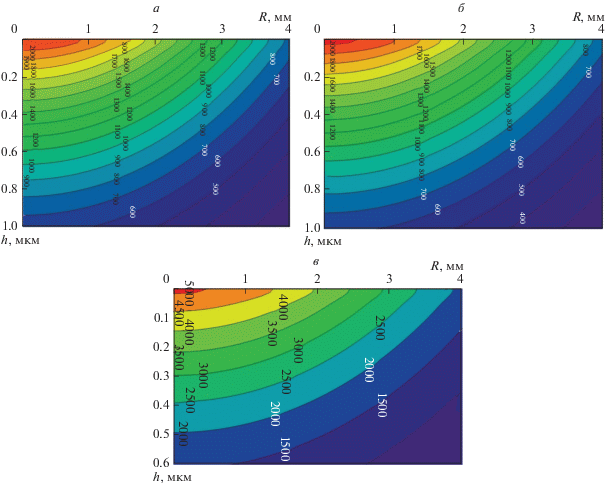
Можно заключить, что со значительным увеличением n (от 300 импульсов и выше) в расчетах должна быть смена тепловой модели полубесконечного тела на модель для тонкой пластины. С учетом этого в результате моделирования получено, что при больших дозах облучения на поверхности достигаются плавильные температуры и температуры кристаллизации в более глубоких слоях образцов АС (рис. 2).

Рис. 2.

Изотермы в АС при 800 импульсах Co70.5Fe0.5Сr4Si7B18 (а), Fe50Ni33B17 (б), Ti50Ni25Cu25 (в).

Численный расчет показал сверхвысокие значения скоростей нагрева и охлаждения АС (табл. 2). На рис. 3 для наглядности представлен характер поведения данных параметров вдоль радиуса зоны облучения и в глубь образца АС Co70.5Fe0.5Сr4Si7B18. Подобное поведение присуще и остальным изученным нами сплавам. Такие скорости являются характерной чертой лазерной закалки [13], которую можно использовать для поверхностного термоупрочнения АС, как это сделано в более ранней работе [14]: при лазерном облучении АС Co70.5Fe0.5Сr4Si7B18 удалость добиться двухстадийного увеличения микротвердости на 20%.

Таблица 2.  

Рассчитанные диапазоны скоростей нагрева и охлаждения для исследованных АС

АС ${{{v}}_{{{\text{наг}}}}} = \frac{{\partial T(0,\tau )}}{{\partial t}},$ °С/с ${{{v}}_{{{\text{охл}}}}} = \frac{{\partial T(0;3\tau )}}{{\partial t}},$ °С/с
Co70.5Fe0.5Сr4Si7B18 8.9 × 109–3.31 × 1010 –1.56 × 109…–5.9 × 107
Fe50Ni33B17 8.6 × 109–3.2 × 1010 –1.5 × 109…–5.7 × 107
Ti50Ni25Cu25 2.6 × 1010–9.7 × 1010 –4.6 × 109…–1.7 × 108
Рис. 3.

Скорость нагрева (а) и охлаждения в момент времени t = 3τ (б) для АС Co70.5Fe0.5Сr4Si7B18.

Обратимся теперь к металлографическим исследованиям экспериментально облученного АС Co70.5Fe0.5Сr4Si7B18. По наблюдению видоизменений рельефа и морфологии поверхности данного АС после ЛИ в работе [14] установлено, что:

– при малом количестве импульсов на облучаемой поверхности АС нет визуальных следов термического воздействия;

– при 400–800 импульсов появляются цвета побежалости (рис. 4а), что является уже результатом нагрева верхнего слоя образцов, соответствующего температурам от 420 до 830°С, если сравнивать с цветами побежалости, наблюдаемыми при обычном печном отжиге.

Рис. 4.

Изменение морфологии поверхностного слоя АС Co70.5Fe0.5Сr4Si7B18, подвергнутого лазерной обработке при разной дозе облучения [14].

– свыше 800 импульсов появляются “индикаторы” значительного разогрева АС, т.е. структуры поверхностного слоя, образованные после локального оплавления образцов, а именно брызги и лунки (рис. 4б, 4в), а также участки с дендритами (рис. 4г).

Таким образом, сопоставляя эти экспериментальные данные с результатами численного моделирования температурных полей, можно заключить удовлетворительное их согласование и соответствие.

С учетом сопоставления расчетных температур максимального нагрева поверхности с температурами кристаллизации исследованных сплавов (табл. 1), можно дать рекомендации по режиму обработки в пределах аморфного состояния малыми дозами ЛИ (до 100 импульсов) для снятия внутренних закалочных напряжений и снижения магнитных потерь. С фиксированными значениями параметров лазерного воздействия, такими как λ = 248 нм, τ = 20 нс, f = 2 Гц, Rs = 4.2 мм, энергию импульсов можно варьировать, однако она не должна превышать 155 мДж для АС Co70.5Fe0.5Сr4Si7B18; ≤120 мДж – для Fe50Ni33B17 и ≤40 мДж – для АС Ti50Ni25Cu25. Увеличение установленных значений Ei будет провоцировать кристаллизацию сплавов, что вполне может быть успешно применено на практике для прицельного изменения конфигураций чередующихся зон аморфной и кристаллической составляющей по поверхности и сечению лент АС.

ЗАКЛЮЧЕНИЕ

Полученные данные и развитые подходы численного моделирования градиентных тепловых полей в АС помогут более целенаправленно использовать лазерное воздействие при изготовлении композитов на основе АС с необходимым составом структурных единиц и структурных параметров: выбирать основные характеристики лазерной установки (например, энергию, мощность, длительность импульса), осуществлять поиск оптимальных и альтернативных режимов ее эксплуатации для необходимого лазерного технологического процесса.

Работа выполнена при финансовой поддержке РФФИ (проект № 20-08-00341-а).

Список литературы

  1. Григорьянц А.Г., Шиганов И.Н., Мисюров А.И. Технологические процессы лазерной обработки: Уч. пособие для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. 664 с.

  2. Shelyakov A.V., Sitnikov N.N., Sheyfer D.V. et al. // Smart Mater. Struct. 2015. V. 24. № 11. Art № 115031.

  3. Mudry S.I., Nykyruy Yu.S., Kulyk Yu.O., Stotsko Z.A. // J. Achiev. Mater. Manufact. Engin. 2013. V. 61. № 1. P. 7.

  4. Fedorov V.A., Yakovlev A.V., Pluzhnikova T.N. et al. // IOP Conf. Ser. 2017. V. 168. Art № 012052.

  5. Smith C., Katakam S., Nag S. et al. // Mater. Lett. 2014. V. 122. P. 155.

  6. Дьюли У. Лазерная технология и анализ материалов. М.: Мир, 1986. 504 с.

  7. Solodov A., Ochkov V. Differential models. An introduction with Mathcad. Berlin, Heidelberg, N.Y.: Springer, 2004. 232 p.

  8. Вейко В.П., Шахно Е.А. Сборник задач по лазерным технологиям СПб.: СПбГУ ИТМО, 2007. 67 с.

  9. Пермякова И.Е., Глезер А.М., Григорович К.В. // Изв. РАН. Сер. физ. 2014. Т. 78. № 10. С. 1246; Permyakova I.E., Glezer A.M., Grigorovich K.V. // Bull. Russ. Acad. Sci. Phys. 2014. V. 78. № 10. P. 996.

  10. Глезер А.М., Манаенков С.Е., Пермякова И.Е., Шурыгина Н.А. // Деформ. и разруш. матер. 2010. № 8. С. 1; Glezer A.M., Manaenkov S.E., Permyakova I.E., Shurygina N.A. // Russ. Metall. (Metally). 2011. V. 2011. № 10. P. 947.

  11. Гундеров Д.В. Трансформация структуры и физико-мех. св-ва кристаллич. и аморф. сплавов систем Nd(Pr)–Fe–B и Ti–Ni при воздействии интенсивной пластической деформации. Дис. … докт. физ.-мат. наук. Уфа: УфГАТУ, 2010. 278 с.

  12. Schlossmacher P., Boucharat N., Rösner H. et al. // J. Phys. IV. 2003. V. 112. P. 731.

  13. Рыкалин Н.Н., Углов А.А., Зуев И.В., Кокора А.Н. Лазерная и электронно-лучевая обработка материалов. М.: Машиностроение, 1985. 496 с.

  14. Пермякова И.Е., Глезер А.М., Иванов А.А., Шеляков А.В. // Изв. вузов. Физ. 2015. Т. 58. № 9. С. 115; Permyakova I.E., Glezer A.M., Ivanov A.A., Shelyakov A.V. // Russ. Phys. J. 2016. V. 58. № 9. P. 1331.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал