Известия РАН. Серия физическая, 2020, T. 84, № 7, стр. 1020-1026

ВВЕДЕНИЕ

Одними из немногих методов, позволяющими реализовать бесконтактную неразрушающую диагностику твердых тел, являются электронно-зондовые методы, основанные на использовании пучков киловольтных электронов низких (примерно до 8–10 кэВ) или средних (от 8–10 до 50 кэВ) энергий. Регистрация информативных сигналов, возбуждаемых в мишени, и сравнение экспериментальных данных с математической моделью изучаемого явления позволяют идентифицировать параметры мишени, которые весьма сложно или даже невозможно определить другими методами [1, 2]. Однако математическое моделирование процессов взаимодействия киловольтных электронов с конденсированным веществом нередко сопряжено с проблемами как чисто математического характера, так и с трудностями проверки разрабатываемых моделей. В полупроводниковом материаловедении при проведении исследований материалов с использованием пучков киловольтных электронов наиболее часто (пожалуй, за исключением рентгеноспектрального микроанализа) в качестве информативного регистрируется сигнал, связанный с генерацией и диффузией в полупроводниковой мишени неравновесных неосновных носителей заряда (ННЗ) и/или регистрируются сигналы, характеристики которых существенно зависят от распределения ННЗ – например ток, наведенный электронным зондом или катодолюминесценция. При этом экспериментальное определение локальных характеристик мишени, облучаемой остро сфокусированным электронным пучком (электронным зондом), в области возбуждения локального сигнала сильно осложнено малым размером этой области (единицы микрометра и менее) [1–3]. Во многом задача электронно-зондовых исследований упрощается при использовании широкого электронного пучка. Это позволяет свести задачу моделирования распределений генерированных киловольтными электронами неравновесных ННЗ к одномерной. Не менее важно и то, что при таких исследованиях реализуется низкий уровень возбуждения изучаемых процессов, что позволяет проще описать их количественно. Такие исследования весьма актуальны для планарных структур, широко используемых в полупроводниковой микро- и наноэлектронике.

В настоящей работе рассмотрены некоторые возможности аналитического матричного метода математического моделирования распределений неравновесных ННЗ в полупроводниковых структурах. Этот метод применительно к задачам теплопроводности в составных пластинах описан в [4]. Однако для решения задач тепломассопереноса в многослойных средах он не получил распространения, возможно, из-за того, что формулы аналитического решения в то время получались исключительно сложными, системы символьных вычислений в то время только начинали зарождаться и потому численные методы были предпочтительными. В работах [5, 6] применены близкие по своей идее методы к описанию явлений переноса на графах в системах контактирующих оболочек и тел вращения, в системах контактирующих стержней, где тепловые потоки определяются матрицей проводимости системы. Ранее в наших работах аналитический матричный метод, предложенный в [4], был применен совместно с аппаратом обобщенных степеней Берса [7–9], что позволило успешно описать в единой форме процесс тепломассопереноса в многослойных средах с различной геометрией: плоских, осесимметричных или слоев с центральной симметрией [10–13].

Отметим также, что, используя классические методы математического моделирования, ранее была решена задача нахождения распределений ННЗ в планарных двух- [14, 15] и трехслойных [16, 17] полупроводниковых структурах для случая постоянства всех электрофизических параметров внутри каждого слоя. В то же время, ввиду сложностей технического характера, распространить этот метод на произвольное число слоев не удалось.

В настоящей работе рассмотрены некоторые возможности использования матричного подхода для моделирования двухслойных полупроводниковых структур конечной толщины. Проведено сравнение аналитических результатов, полученных с использованием матричного метода, с результатами расчетов, полученных с помощью численного метода конечных разностей. Модельные расчеты проведены для электрофизических параметров, характерных для твердого раствора кадмий–ртуть–теллур–теллурид кадмия, широко используемого при производстве приборов инфракрасной техники [18, 19].

ПОСТАНОВКА ЗАДАЧИ

В случае одномерной диффузии в конечный полупроводник вдоль оси OZ, перпендикулярной поверхности двухслойной полупроводниковой структуры $\left( {z \in \left[ {0,l} \right]} \right),$ распределение ННЗ по глубине находится как решение дифференциального уравнения

с граничными условиями

Для двухслойной структуры введем обозначения: ${{D}_{1}},$ ${{D}_{2}},$ ${{L}_{1}},$ ${{L}_{2}},$ ${{\tau }_{1}},$ ${{\tau }_{2}}$ – электрофизические параметры первого и второго слоев: коэффициенты диффузии, диффузионные длины и времена жизни ННЗ, соответственно; ${{\nu }_{{{{s}_{1}}}}}$ и ${{\nu }_{{{{s}_{2}}}}}$ – скорости поверхностной рекомбинации ННЗ в первом и втором слоях, а ${{S}_{1}},$ и ${{S}_{2}}$ – приведенные скорости поверхностной рекомбинации, соответственно, на поверхностях первого (при $z = 0$) и второго (при $z = l$) материалов. При этом ${{L}_{1}} = \sqrt {{{D}_{1}}{{\tau }_{1}}} ,$ ${{L}_{2}} = \sqrt {{{D}_{2}}{{\tau }_{2}}} ,$ и ${{S}_{1}} = {{{{L}_{1}}{{\nu }_{{{{s}_{1}}}}}} \mathord{\left/ {\vphantom {{{{L}_{1}}{{\nu }_{{{{s}_{1}}}}}} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}},$ ${{S}_{2}} = {{{{L}_{2}}{{\nu }_{{{{s}_{2}}}}}} \mathord{\left/ {\vphantom {{{{L}_{2}}{{\nu }_{{{{s}_{2}}}}}} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}.$ Функция $\Delta p\left( z \right)$ описывает распределение по глубине неравновесных ННЗ, генерированных внешним энергетическим воздействием, после их диффузии в полупроводнике, при этом $z$ – координата, отсчитываемая от плоской поверхности облучаемой мишени вглубь полупроводника. Функция $\rho \left( z \right)$ – зависимость от координаты плотности ННЗ, генерированных электронным пучком в полупроводниковой мишени. Для широкого электронного пучка $\rho \left( z \right)$ может быть найдена из выражения для плотности энергии электронного пучка $\rho {\text{*}}\left( z \right){\text{:}}$

выделяемой в мишени в единицу времени до начала процесса диффузии [2, 20–22 ], делением $\rho {\text{*}}\left( z \right)$ на энергию образования электронно-дырочной пары. Здесь ${{E}_{0}}$ – энергия электронного пучка, рассеянная в мишени в единицу времени, ${{z}_{{ms}}}$ – глубина максимальных потерь энергии первичными электронами, испытавшими малоугловое рассеяние и поглощенными мишенью; ${{z}_{{ss}}} = {{Z}^{{ - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{z}_{{ms}}}$ – глубина максимальных потерь энергии обратно рассеянными электронами, испытавшими в мишени рассеяние на большие углы и вышедшими из мишени, Z – атомный номер вещества мишени; $\eta $ – коэффициент обратного рассеяния электронов пучка, $\eta = {{0.024e{{Z}^{{1.67}}}} \mathord{\left/ {\vphantom {{0.024e{{Z}^{{1.67}}}} A}} \right. \kern-0em} A},$ А – относительная атомная масса вещества мишени. Отметим, что для электронов с энергией ${{E}_{0}}$[кэВ] значение ${{z}_{{ms}}}$ для мишени плотности ${{\rho }_{0}}$ [г/см³] может быть определено из диффузионной модели [23]:

Здесь $R{\text{*}}$ – полный пробег электронов пучка в мишени.

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ

Опишем кратко суть совместного применения аппарата обобщенных степеней Берса и аналитического матричного метода.

В общем виде одномерный стационарный процесс тепломассопереноса в многослойной среде может быть задан уравнением

где потенциал ${{\Phi }^{{(i)}}}(z)$ – искомая функция, $D_{1}^{{(i)}}$ = = $a_{1}^{{(i)}}(z){d \mathord{\left/ {\vphantom {d {dz}}} \right. \kern-0em} {dz}}$ и $D_{2}^{{(i)}}$ = $a_{2}^{{(i)}}(z){d \mathord{\left/ {\vphantom {d {dz}}} \right. \kern-0em} {dz}}$ – дифференциальные операторы, $a_{1}^{{(i)}}(z)$ и $a_{2}^{{(i)}}(z)$ – положительные функции, определенные физическими и геометрическими параметрами слоев, $\mu _{{}}^{{(i)}}(z)$ – величина, пропорциональная объемной плотности энергии источников, i – номер слоя, который совпадает с номером левой координаты этого слоя. Поток задается формулой ${{J}^{{(i)}}}(z)$ = $ - D_{1}^{{(i)}}{{\Phi }^{{(i)}}}(z).$ В точке контакта слоев выполняются условия типа идеального контакта, т.е. справедливы условия непрерывности потенциала и потока:

Введем вектор-столбцы V, W и матрицу K

Здесь w⁽ⁱ⁾(z) – некоторое частное решение уравнения (3) для i-го слоя, ${{X}_{i}}(z,{{z}_{i}})$ и ${{\tilde {X}}_{i}}(z,{{z}_{i}})$ – обобщенная степень Берса и присоединенная обобщенная степень Берса на интервале $({{z}_{i}},\;{{z}_{{i + 1}}})$ соответственно.

При заданных ${{\Phi }^{{(1)}}}({{z}_{1}})$ и ${{J}^{{(1)}}}({{z}_{1}})$ с учетом условий (5), получим [24]

где ${{W}^{{(0)}}}({{z}_{1}}) = 0,$ ${{L}^{{(i,j)}}}(z,{{z}_{j}})$ = ${{K}^{{(i)}}}(z,{{z}_{i}}){{K}^{{(i - 1)}}}({{z}_{i}},{{z}_{{i - 1}}})$ … ${{K}^{{(j)}}}({{z}_{{j + 1}}},{{z}_{j}}),$ $i \geqslant j,$ ${{z}_{i}} \leqslant z \leqslant {{z}_{{i + 1}}}.$

Формула (6) дает точное аналитическое решение задачи Коши для уравнения (4) при произвольном количестве слоев.

В конечной точке системы слоев, следуя (6), получим

Формула (7) связывает значения потенциала и потока в первой и последней точке системы слоев, что позволяет в общем случае сводить решение краевой задачи первого, второго или третьего типа при любом конечном числе слоев к решению системы двух линейных уравнений с двумя неизвестными.

Таким образом, аналитический матричный метод можно применять к решению краевых задач тепломассопереноса первого, второго или третьего типов для системы (4) в многослойной среде с любым конечным числом слоев.

Применяя данный метод для решения дифференциального уравнения (1), (2), описывающего диффузию ННЗ, генерированных широким электронным пучком в многослойной полупроводниковой мишени, получим, что $a_{1}^{{(i)}}(z) = {{D}^{{(i)}}}$ в i-ом слое, и $a_{2}^{{(i)}}(z) = {{\tau }^{{(i)}}}$ ННЗ в i-ом слое, m = 1, а ${{\mu }^{{(i)}}}(z)$ = = $ - {{\tau }^{{(i)}}}{{\rho }^{{(i)}}}(z),$ где ${{\rho }^{{(i)}}}(z)$ – плотность ННЗ, генерированных в полупроводнике в i-ом слое. При постоянных коэффициентах уравнения на i-ом слое матрица K принимает вид

При проведении расчетов матричным методом в рассматриваемой задаче использовалось следующее частное решение для уравнения диффузии ННЗ (1):

где ${{K}_{1}}$ = $ - \frac{{1.085\left( {1 - \eta } \right){{E}_{0}}L}}{{4D\left( {1 - \eta + {{\eta {{z}_{{ss}}}} \mathord{\left/ {\vphantom {{\eta {{z}_{{ss}}}} {{{z}_{{ms}}}}}} \right. \kern-0em} {{{z}_{{ms}}}}}} \right)}},$ ${{K}_{2}}$ = = $ - \frac{{1.085{{z}_{{ss}}}{{E}_{0}}L\eta }}{{4D{{z}_{{ms}}}\left( {1 - \eta + {{\eta {{z}_{{ss}}}} \mathord{\left/ {\vphantom {{\eta {{z}_{{ss}}}} {{{z}_{{ms}}}}}} \right. \kern-0em} {{{z}_{{ms}}}}}} \right)}}.$

ЧИСЛЕННОЕ РЕШЕНИЕ МАТРИЧНЫМ МЕТОДОМ

Разобьем длину l полупроводниковой структуры на m отрезков и обозначим точки разбиения ${{z}_{j}},$ где j – номер точки, $j = \overline {1,\,\,m + 1} ,$ причем ${{z}_{1}} = 0$ и ${{z}_{{n + 1}}} = l.$ Правую часть уравнения (1) аппроксимируем некоторой функцией ${{f}^{{(j)}}}(z)$ на каждом отрезке разбиения $z \in [{{z}_{j}},{{z}_{{j + 1}}}].$ Обозначим ${{w}^{{(j)}}}(z)$ – частное решение уравнения (1) на отрезке $z \in [{{z}_{j}},{{z}_{{j + 1}}}]$ с ${{f}^{{(j)}}}(z)$ в правой части.

В каждой точке ${{z}_{j}}$ найдем числовые значения матриц W и K, учитывая номер слоя i, на который попадает точка ${{z}_{j}}{\text{:}}$

Тогда

В данной формуле элементы V⁽¹⁾(z₁) при решении задачи (1), (2) изначально неизвестны. Связав ${{V}^{{(1)}}}({{z}_{1}})$ и ${{V}^{{(m + 1)}}}({{z}_{{m + 1}}})$ и решив систему линейных уравнений с двумя неизвестными, найдем ${{V}^{{(1)}}}({{z}_{1}}),$ а затем и ${{V}^{{(j)}}}({{z}_{j}})$ для всех $j = \overline {1,\,\,m + 1} .$

ЧИСЛЕННОЕ РЕШЕНИЕ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ

Для дифференциальной задачи (1), (2) построена консервативная разностная схема на равномерной сетке ${{\bar {D}}_{h}}$ = $\left\{ {{{z}_{i}} = ih,\,\,i = 0,...,N,\,\,h = {l \mathord{\left/ {\vphantom {l N}} \right. \kern-0em} N}} \right\}$ [25]:

где ${{a}_{i}} = {{\left( {\frac{1}{h}\int_{{{z}_{{i - 1}}}}^{{{z}_{i}}} {\frac{{dz}}{{D\left( z \right)}}} } \right)}^{{ - 1}}}$ = ${{\left( {\int_{ - 1}^0 {\frac{{ds}}{{D\left( {{{z}_{i}} + sh} \right)}}} } \right)}^{{ - 1}}},$ ${{d}_{i}}$ = = $\int_{ - 0.5}^{0.5} {\frac{{ds}}{{\tau \left( {{{z}_{i}} + sh} \right)}}} ,$ ${{\varphi }_{i}}$ = $\int_{ - 0.5}^{0.5} {\rho \left( {{{z}_{i}} + sh} \right)ds} .$ Здесь $\Delta {{p}_{i}}$ – приближенное значение точного решения $\Delta p({{z}_{i}}),$ ${{\rho }_{i}} = \rho ({{z}_{i}}),$ а интегралы заменены их приближенными выражениями:

Систему (8) решали методом прогонки.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Результаты математического моделирования явлений тепломассопереноса, обусловленного взаимодействием электронных пучков с однородными полупроводниками или многослойными планарными полупроводниковыми структурами, во многом будут определяться характером потерь энергии электронами пучка в мишени. Рассмотрим этот вопрос для диапазона энергий электронов 10–50 кэВ, широко используемых в электронно-зондовых технологиях.

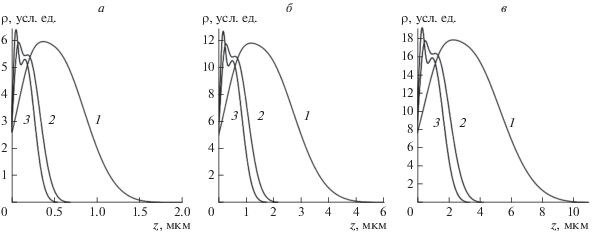
Зависимости от координаты плотности ННЗ, генерированных электронным пучком в классических монокристаллических мишенях: в кремнии (легкий полупроводник), арсениде галлия (полупроводник со средними значениями параметров) и теллуриде кадмия (тяжелый полупроводник), рассчитанные для энергии электронов 10, 20 и 30 кэВ, – представлены на рис. 1. Характер кривых во многом зависит от значений глубины максимальных потерь энергии первичными электронами, испытавшими малоугловое рассеяние и поглощенными мишенью ${{z}_{{ms}}},$ и глубины максимальных потерь энергии обратно рассеянными электронами, испытавшими в мишени рассеяние на большие углы и вышедшими из мишени ${{z}_{{ss}}}.$ При рассматриваемых энергиях электронов первичного пучка для легких материалов (Si) разница в значениях ${{z}_{{ms}}}$ и ${{z}_{{ss}}}$ небольшая. Как следствие этого, суммарная зависимость плотности потерь энергии электронами пучка со средними энергиями (от 8–10 до 50 кэВ) – а, значит, и зависимость $\rho \left( z \right),$ имеют вид, близкий к классической функции Гаусса (см. рис. 1а, кривые 1). Иной вид имеют подобные зависимости для полупроводников со средними и большими значениями параметров: значениями плотности ${{\rho }_{0}},$ порядкового номера Z и относительной атомной массы A (см. рис. 1, кривые 2 и 3). В этом случае значения ${{z}_{{ms}}}$ и ${{z}_{{ss}}}$ отличаются довольно сильно, так что при сложении двух функций типа Гаусса (3) это приводит к появлению в зависимостях $\rho {\text{*}}\left( z \right)$ второго локального максимума, обусловленного вкладом в функцию $\rho {\text{*}}\left( z \right)$ обратно рассеянных электронов. Отметим, что учет влияния обратно рассеянных электронов оказался весьма важным и при оценке нагрева полупроводниковых мишеней электронным зондом [26–28].

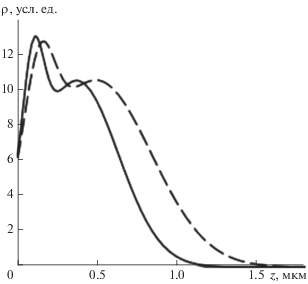
Из результатов расчетов, проведенных для различных полупроводниковых мишеней, следует, что для тяжелых полупроводниковых мишеней при энергии электронов, большей примерно 20 кэВ, величина плотности поглощенной энергии при значениях z до примерно 0.6 мкм меняется незначительно. В качестве иллюстрации на рис. 2 представлен вид распределений плотностей потерь энергии электронами пучка в монокристаллических CdTe и ${\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te,}}$ широко используемых при производстве приборов инфракрасной техники [18, 19]. Расчеты проведены для энергии электронов пучка ${{E}_{0}} = 20$ кэВ. Это позволяет для оценки распределений неравновесных ННЗ в многослойных планарных полупроводниковых материалах не учитывать изменения спектров энергии электронов, прошедших пленочную мишень заданной толщины [29, 30].

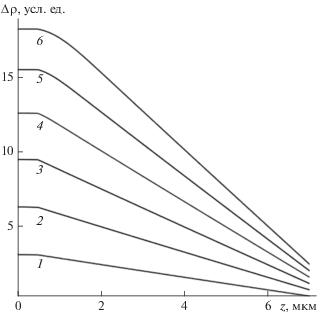
Результаты оценки распределений ННЗ, генерированных электронным пучком в двухслойной полупроводниковой структуре ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}$ толщиной 7 мкм (0.5 мкм – ${\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}$ и 6.5 мкм – CdTe) для различных энергий электронов пучка: 5 (кривая 1), 10 (2), 15 (3), 20 (4), 25 (5) и 30 кэВ (6) – представлены на рис. 3. Использованы следующие значения параметров: ${{L}_{1}} = 35$ мкм, ${{\tau }_{1}} = {{10}^{{ - 6}}}$ с, ${{S}_{1}} = 0.0857$ для первого материала (пленки); ${{L}_{2}} = 30$ мкм, ${{\tau }_{2}} = {{10}^{{ - 5}}}$ с, ${{S}_{2}} = 10$ – для второго материала (подложки). Значение ${{z}_{1}} = 0.5$ мкм, $l = 7$ мкм. Толщина пленки в рассматриваемом случае довольно большая, поэтому при повышении энергии первичного пучка электронов центр тяжести распределений потерь энергии смещается в объем полупроводника, при этом влияние первой поверхности (при $z = 0$) уменьшается, а влияние второй поверхности (при $z = l$) на процесс потерь энергии практически отсутствует (см. рис. 1 и 2). Как следствие этого увеличивается количество ННЗ, участвующих в диффузионном процессе, что наблюдается на зависимостях $\Delta p(z).$ Поскольку расчеты проводились для пленочной структуры, характер спада распределений ННЗ в объеме пленки отличается от аналогичных зависимостей, характерных для полубесконечных полупроводников (см., например, [14, 17]): на второй поверхности пленки (при $z = l$) концентрации ННЗ отличны от нуля.

Проведено сравнение применения аналитического матричного метода и численного метода конечных разностей для нахождения распределений ННЗ, генерированных электронным пучком в рассматриваемой двухслойной полупроводниковой структуре ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}}.$ Численное решение рассчитано на сетке из 450 ячеек с шагом $h = {\text{0}}{\text{.0067}}$ мкм. Результаты расчетов аналитическим методом и численным методом конечных разностей практически совпадают и потому на рисунке не выделены.

Расчеты проведены с помощью математических пакетов Maple и Matlab (MathWorks, Inc.) версии 7.5.0.342 на персональном компьютере со следующими характеристиками: процессор Intel Pentium E5400 (2 × 2.70 Ггц, 2 МБ Cache), объем оперативной памяти – 2 ГБ. Затраты машинного времени на расчет распределений ННЗ аналитическим и численным методами составили около 2 с, что говорит о практической применимости предложенного аналитического матричного метода для решения рассматриваемой задачи.

ЗАКЛЮЧЕНИЕ

Изложен аналитический матричный метод математического моделирования явлений тепломассопереноса, обусловленного взаимодействием широких электронных пучков с многослойными планарными полупроводниковыми структурами. Рассмотрены некоторые возможности использования этого метода для оценки распределений неравновесных неосновных носителей заряда в многослойных планарных полупроводниковых структурах. Для электрофизических параметров, характерных для двухслойной структуры ${{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} \mathord{\left/ {\vphantom {{{\text{C}}{{{\text{d}}}_{{{\text{0}}{\text{.2}}}}}{\text{H}}{{{\text{g}}}_{{{\text{0}}{\text{.8}}}}}{\text{Te}}} {{\text{CdTe}}}}} \right. \kern-0em} {{\text{CdTe}}}},$ проведено сравнение результатов расчетов с использованием аналитического матричного метода с результатами расчетов с помощью численной консервативной разностной схемы. Показано, что предложенный матричный метод позволяет проводить расчеты распределений ННЗ за сравнительно короткое время с точностью, достаточной для практического использования в электронно-зондовых технологиях.

Исследования проведены при финансовой поддержке Российского фонда фундаментальных исследований (проект № 19-03-00271), а также РФФИ и правительства Калужской области (проект № 18-41-400001).