Известия РАН. Серия физическая, 2020, T. 84, № 9, стр. 1286-1289

Метод акустической спектроскопии используется для определения свойств или структуры веществ посредством исследования частотных зависимостей скорости распространения и затухания ультразвуковых волн [1]. Затухание ультразвука, вызванное поглощением или рассеянием ультразвуковых волн на неоднородностях среды, а также релаксационными эффектами, неизбежно приводит к частотной зависимости скорости звука (упругой дисперсии). Использование акустической спектроскопии в традиционном исполнении для гетерогенных сред, а также неоднородных твердых тел с размерами неоднородностей структуры, близкими к длине волны, связано с существенными трудностями [2].

В настоящей работе предложен новый метод акустической спектроскопии, пригодный для комплексной характеризации пьезоматериалов с высокими упругими потерями и дисперсией.

Комплексные упругие, диэлектрические и пьезоэлектрические параметры пористой пьезокерамики, а также их частотные зависимости изучали методом анализа пьезорезонансных спектров для основной и высших гармоник толщинной моды колебаний пьезоэлектрических элементов (PRAP) [3]. Программа PRAP использует обобщенную форму метода Смита для определения свойств материала для произвольной стандартной резонансной моды и обобщенный метод отношений для радиальной моды [3], справедливый для материалов с произвольной добротностью.

Для характеризации пьезоэлектрического элемента с помощью анализа пьезорезонансных спектров используется соотношение для импеданса $Z$:

где V – напряжение, I – ток, и A – площадь поверхности, по которой измеряется ток. Пьезоэлектрические уравнения дают соотношение между индукцией D и электрическим полем E через деформацию S и механическое напряжение T. Для простых одномерных резонансных мод ряд электрических и механических переменных обращаются в нуль, и наборы пьезоэлектрических уравнений развязываются.

Путем решения волнового уравнения для одномерного смещения в установившимся режиме в образце и оценки S из производной смещения с учетом граничных условий для незажатого резонатора, пьезоэлектрические уравнения могут быть использованы для оценки соотношения между D и E как функции частоты и свойств материала. Импеданс резонатора, совершающего колебания растяжения–сжатия по толщине (мода ТЕ), сводится к [4]:

где $C_{{33}}^{D}$ – модуль упругости при постоянной индукции, $\beta _{{33}}^{S}$ – диэлектрическая восприимчивость зажатого образца, h₃₃ – пьезоконстанта, ρ – плотность образца, $\omega $ – угловая частота и l – толщина образца в направлении поляризации. При характеризации пьезоэлектрических материалов методом импедансной спектроскопии, свойства материала в уравнении (2) могут подбираться до тех пор, пока импеданс совпадет с измеренным спектром импеданса как функции частоты.

В качестве объекта для исследования был выбран керамоматричный пьезокомпозит, представляющий собой пористую сегнетопьезокерамику на основе цирконата-титаната свинца (ЦТС) состава PbTi_0.45Zr_0.53(W_1/2Cd_1/2)_0.02O₃ с произвольно распределенными порами размером d = 10–20 мкм и относительной пористостью $\rho $ от 18 до 26% [5].

Измерения комплексных упругих, диэлектрических и пьезоэлектрических параметров пьезоэлементов, а также их частотных зависимостей выполняли с помощью анализатора импеданса Agilent 4294A и программы анализа резонансных спектров PRAP. Измерения выполняли со стандартной точностью: основная погрешность измерения импеданса $Z$ – ± 0.08%, частота испытательного сигнала   f – от 40 Гц до 110 МГц, разрешение по частоте – 1 мГц, погрешность установки частоты – ±20 мкГц. Погрешности определения комплексных упругих, диэлектрических и пьезоэлектрических констант пьезоматериала определяются указанной погрешностью измерения импеданса $Z$ и погрешностью установки частоты f, а также точностью изготовления пьезоэлектрических элементов.

На рис. 1 в качестве примера показана микроструктура пористой пьезокерамики PbTi_0.45Zr_0.53(W_1/2Cd_1/2)_0.02O₃ с относительной пористостью ρ = 18%. Пористая керамика характеризуется наличием пор неправильной формы со средним размером d = 10–30 мкм с существенным присутствием более мелких пор с размерами, соответствующими размеру зерен керамики.

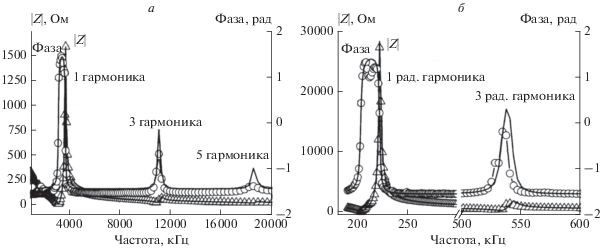
На рис. 2 приведены измеренные импедансные спектры, а также их аппроксимации, выполненные с помощью программы PRAP, для толщинной (TE) и радиальной (RE) мод колебаний пористого пьезокерамического диска PbTi_0.45Zr_0.53(W_1/2Cd_1/2)_0.02O₃. Использование PRAP анализа для основной и высших гармоник колебаний пьезоэлемента позволяет не только определить комплексные упругие, диэлектрические и пьезоэлектрические параметры пьезоактивных материалов, но и исследовать их частотные зависимости в широком диапазоне частот [6, 7].

Комплексные константы пористой пьезокерамики PbTi_0.45Zr_0.53(W_1/2Cd_1/2)_0.02O₃ с относительной пористостью ρ = 18%, полученные с помощью PRAP аппроксимации импедансных спектров (рис. 2) для основных гармоник RE и TE мод колебаний, а также результаты, полученные с использованием Стандарта IEEE [8], приведены в табл. 1.

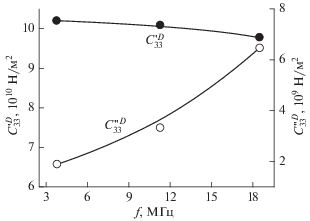
Частотные зависимости действительной и мнимой частей комплексного модуля упругости, полученные в результате анализа импедансных спектров (рис. 2а) для высших гармоник ТЕ моды колебаний пористого пьезокерамического диска, показаны на рис. 3. Из рис. 3 видно, что действительная часть модуля упругости $C_{{33}}^{{'D}}$ убывает (аномальная дисперсия), а мнимая часть $C_{{33}}^{{''D}}$ увеличивается с ростом частоты. Согласно [9], увеличение затухания ультразвуковых волн (упругие потери $Q_{M}^{{ - 1}}$ = ${{C_{{33}}^{{''D}}} \mathord{\left/ {\vphantom {{C_{{33}}^{{''D}}} {C_{{33}}^{{'D}}}}} \right. \kern-0em} {C_{{33}}^{{'D}}}}$), независимо от его характера и природы, должно приводить к увеличению скорости звука $V_{t}^{D}$ = $\sqrt {{{C_{{33}}^{{'D}}} \mathord{\left/ {\vphantom {{C_{{33}}^{{'D}}} \rho }} \right. \kern-0em} \rho }} .$ Увеличение $C_{{33}}^{{''D}}$ в нашем случае обусловлено релеевским рассеянием упругих волн на порах ($\lambda \gg d,$ где λ – длина волны, а d – средний размер пор). При увеличении частоты механизм рассеяния изменяется от рэлеевского к стохастическому (4 ≤ λ/D ≤ 10) [10]. Аномальное поведение $C_{{33}}^{{'D}}$ связано с изменением масштабного фактора (λ/D) и формированием “квазистержневой” структуры пористой керамики, для которой скорость звука определяется не упругим модулем $C_{{33}}^{{'D}},$ а упругой податливостью $S_{{33}}^{{'D}}$ $\left( {V = \sqrt {{{S_{{33}}^{{'D}}} \mathord{\left/ {\vphantom {{S_{{33}}^{{'D}}} \rho }} \right. \kern-0em} \rho }} } \right)$ [11].

Результаты проведенных исследований показали, что предложенный метод акустической спектроскопии с использованием анализа резонансных спектров (PRAP) высших гармоник толщинных колебаний пьезоэлементов может быть использован для комплексной характеризации пьезоматериалов с высокими упругими потерями и дисперсией. Разработанный метод позволяет определить комплексные упругие, диэлектрические и пьезоэлектрические параметры пьезоактивных материалов, а также их частотные зависимости в широком диапазоне частот, недоступном для обычных методов исследования с использованием полуволновых пьезоэлементов из-за их малой толщины.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ (государственное задание в сфере научной деятельности, Южный федеральный университет, 2020).