Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 39-46

Межзонное поглощение света в сверхрешетке, состоящей из чередующихся полосок однослойного и двухслойного графена

П. В. Бадикова^1, *, Д. В. Завьялов¹, В. И. Конченков¹, С. В. Крючков^1, 2

¹ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования “Волгоградский государственный технический университет”
Волгоград, Россия

² Федеральное государственное бюджетное образовательное учреждение высшего образования “Волгоградский государственный социально-педагогический университет”
Волгоград, Россия

^* E-mail: polin.badicova@gmail.com

Поступила в редакцию 20.07.2020
После доработки 28.08.2020
Принята к публикации 28.09.2020

DOI: 10.31857/S036767652101004X

Полный текст (PDF)

Аннотация

Исследована модель сверхрешетки, состоящей из чередующихся областей однослойного и двухслойного графена, энергетическим спектром которой можно управлять при помощи внешнего электрического поля, перпендикулярного поверхности образца. Показано, что энергетический спектр такой структуры может быть аппроксимирован моделью Кейна. Вычислен коэффициент межзонного поглощения для такой сверхрешетки.

ВВЕДЕНИЕ

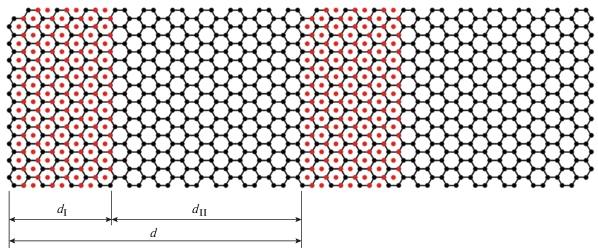
Появление эффективных источников терагерцевого излучения в последние годы (см., например, [1]) и широкие перспективы использования волн этого диапазона в медицинской диагностике стимулируют исследования твердотельных структур, подходящих для создания детекторов терагерцевого излучения. Среди таких структур – полупроводниковые и графеновые сверхрешетки (СР), параметры которых можно регулировать на этапе изготовления. В настоящей работе вычислен коэффициент межзонного поглощения света в сверхрешетке, состоящей из чередующихся полосок однослойного и двухслойного графена, энергетическим спектром которой можно управлять, прикладывая постоянное электрическое поле, перпендикулярное поверхности образца (рис. 1). Красным цветом показаны атомы второго слоя графена. Относительное расположение слоев в областях двухслойного графена соответствует типу AB, графен такого типа иначе называется Bernal stacking graphene [2, 3]. Такая СР рассмотрена в [4], где с использованием модели Кронига–Пенни и метода Т-матрицы выведено дисперсионное уравнение, результаты аналитического рассмотрения сравниваются с результатами моделирования методами теории функционала плотности. При квантовохимическом моделировании период СР полагался равным 10.9 нм, что соответствует 51 периоду основной решетки графена. Поперечное электрическое поле позволяет управлять шириной запрещенной зоны в спектре СР за счет нарушения эквивалентности между состояниями в различных слоях двухслойного графена. Таким образом, при помощи электрического поля можно смещать край межзонного поглощения света рассматриваемой структурой и использовать рассматриваемую СР для измерения частоты падающего на образец излучения. Возможность управления спектром различных типов графеновых сверхрешеток (ГСР) при помощи электрического поля исследовалось также в [5‒8], в [9] рассмотрено влияние электрического поля на спектр СР на основе монослоя нитрида бора. В [10] исследуется эффект увлечения в гетероструктуре, состоящей из фрагментов однослойного и двухслойного графена. В [11, 12] исследуются электронные состояния в гетеропереходе однослойный – двухслойный графен.

Рис. 1.

Схема размещения полосок графена, формирующих двухслойные области, на основном графеновом листе.

ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА СВЕРХРЕШЕТКИ, СОСТОЯЩЕЙ ИЗ ЧЕРЕДУЮЩИХСЯ ПОЛОСОК ОДНОСЛОЙНОГО И ДВУХСЛОЙНОГО ГРАФЕНА

Энергетический спектр двухслойного графена, помещенного в постоянное электрическое поле, перпендикулярное поверхности образца, имеет вид [2, 3]:

(1)

$\varepsilon = \pm \sqrt {{{\Delta }^{2}} + \upsilon _{F}^{2}{{p}^{2}} + \frac{{t_{ \bot }^{2}}}{2} \pm \sqrt {\upsilon _{F}^{2}{{p}^{2}}\left( {4{{\Delta }^{2}} + t_{ \bot }^{2}} \right) + \frac{{t_{ \bot }^{4}}}{4}} } .$

Здесь υ_F – скорость на поверхности Ферми в графене, t_⊥ ≈ 0.4 эВ – интеграл перекрытия между слоями двухслойного графена, Δ – полуширина запрещенной зоны в энергетическом спектре этого материала, которая непосредственно зависит от постоянного электрического поля, приложенного перпендикулярно поверхности образца, p – модуль квазиимпульса электрона в двухслойном графене.

Рассмотрим особенности спектра графеновой сверхрешетки, состоящей из чередующихся полосок однослойного и двухслойного графена. Период сверхрешетки обозначим d, ширина полоски однослойного графена d_I, ширина полоски двухслойного графена d_II. Подобная ГСР исследовалась ранее в [13], где, однако, влияние поперечного поля не учитывалось.

В [4] с использованием метода трансляционной матрицы и модели Кронига–Пенни выведено дисперсионное соотношение для рассматриваемой СР, в общем случае имеющее вид

(2)

$F\left( {\varepsilon ,{{q}_{x}},{{q}_{y}}} \right) = 0,$

где ε – энергия электрона, q_x,_y = p_x,_yd/ħ. Перейдем к безразмерным переменным: a_I= d_I/d, a_II= d_II/d, B = ħυ_F/(t_⊥d), величины ε и Δ будем измерять в единицах t_⊥. Введем обозначения

(3)

$Q_{2}^{ + } = q_{y}^{2} - \frac{{{{\Delta }^{2}} + {{\varepsilon }^{2}}}}{{{{B}^{2}}}} + \frac{{\sqrt {\left( {4{{\Delta }^{2}} + 1} \right){{\varepsilon }^{2}} - {{\Delta }^{2}}} }}{{{{B}^{2}}}},$

(4)

$Q_{2}^{ - } = q_{y}^{2} - \frac{{{{\Delta }^{2}} + {{\varepsilon }^{2}}}}{{{{B}^{2}}}} - \frac{{\sqrt {\left( {4{{\Delta }^{2}} + 1} \right){{\varepsilon }^{2}} - {{\Delta }^{2}}} }}{{{{B}^{2}}}},$

(5)

${{Q}_{1}} = \frac{{{{\varepsilon }^{2}}}}{{{{B}^{2}}}}q_{y}^{2}.$

(6)

$\begin{gathered} {{F}_{1}} = 2\cos {{q}_{1}}{{a}_{{\text{I}}}}{\text{ch}}{{q}_{2}}{{a}_{{{\text{II}}}}} + \\ + \,\,\frac{{{{\varepsilon }^{2}}\left( {q_{1}^{2} - q_{2}^{2}} \right) + {{\Delta }^{2}}\left( {q_{y}^{2} - q_{1}^{2}} \right)}}{{\left( {{{\Delta }^{2}} - {{\varepsilon }^{2}}} \right){{q}_{1}}{{q}_{2}}}}\sin {{q}_{1}}{{a}_{{\text{I}}}}{\text{sh}}{{q}_{2}}{{a}_{{{\text{II}}}}} - \\ - \,\,2\cos {{q}_{x}}, \\ \end{gathered} $

(7)

$\begin{gathered} {{F}_{2}} = 2\cos {{q}_{1}}{{a}_{{\text{I}}}}\cos {{q}_{2}}{{a}_{{{\text{II}}}}} + \\ + \,\,\frac{{{{\varepsilon }^{2}}\left( {q_{1}^{2} + q_{2}^{2}} \right) + {{\Delta }^{2}}\left( {q_{y}^{2} - q_{1}^{2}} \right)}}{{\left( {{{\Delta }^{2}} - {{\varepsilon }^{2}}} \right){{q}_{1}}{{q}_{2}}}}\sin {{q}_{1}}{{a}_{{\text{I}}}}\sin {{q}_{2}}{{a}_{{{\text{II}}}}} - \\ - \,\,2\cos {{q}_{x}}, \\ \end{gathered} $

(8)

$\begin{gathered} {{F}_{3}} = 2{\text{ch}}{{q}_{1}}{{a}_{{\text{I}}}}{\text{ch}}{{q}_{2}}{{a}_{{{\text{II}}}}} + \\ + \,\,\frac{{ - {{\varepsilon }^{2}}\left( {q_{1}^{2} + q_{2}^{2}} \right) + {{\Delta }^{2}}\left( {q_{y}^{2} + q_{1}^{2}} \right)}}{{\left( {{{\Delta }^{2}} - {{\varepsilon }^{2}}} \right){{q}_{1}}{{q}_{2}}}}{\text{sh}}{{q}_{1}}{{a}_{{\text{I}}}}{\text{sh}}{{q}_{2}}{{a}_{{{\text{II}}}}} - \\ - \,\,2\cos {{q}_{x}}, \\ \end{gathered} $

(9)

$\begin{gathered} {{F}_{4}} = 2{\text{ch}}{{q}_{1}}{{a}_{{\text{I}}}}\cos {{q}_{2}}{{a}_{{{\text{II}}}}} + \\ + \,\,\frac{{ - {{\varepsilon }^{2}}\left( {q_{1}^{2} - q_{2}^{2}} \right) + {{\Delta }^{2}}\left( {q_{y}^{2} + q_{1}^{2}} \right)}}{{\left( {{{\Delta }^{2}} - {{\varepsilon }^{2}}} \right){{q}_{1}}{{q}_{2}}}}{\text{sh}}{{q}_{1}}{{a}_{{\text{I}}}}\sin {{q}_{2}}{{a}_{{{\text{II}}}}} - \\ - \,\,2\cos {{q}_{x}}. \\ \end{gathered} $

Первое семейство дисперсионных поверхностей ε_i (q_x,q_y) получается из решения (2) при учете следующих соотношений:

(10)

$\left\{ \begin{gathered} {{Q}_{1}} \geqslant 0,\,\,\,Q_{2}^{ + } \geqslant 0{\text{:}}\,{{q}_{1}} = \sqrt {{{Q}_{1}}} ,\,\,\,{{q}_{2}} = \sqrt {Q_{2}^{ + }} ,\,\,\,F = {{F}_{1}}; \hfill \\ {{Q}_{1}} \geqslant 0,\,\,\,Q_{2}^{ + } < 0{\text{:}}\,{{q}_{1}} = \sqrt {{{Q}_{1}}} ,\,\,\,{{q}_{2}} = \sqrt { - Q_{2}^{ + }} ,\,\,\,F = {{F}_{2}}; \hfill \\ {{Q}_{1}} < 0,\,\,\,Q_{2}^{ + } \geqslant 0{\text{:}}\,{{q}_{1}} = \sqrt { - {{Q}_{1}}} ,\,\,\,{{q}_{2}} = \sqrt {Q_{2}^{ + }} ,\,\,\,F = {{F}_{3}}; \hfill \\ {{Q}_{1}} < 0,\,\,\,Q_{2}^{ + } < 0{\text{:}}\,{{q}_{1}} = \sqrt { - {{Q}_{1}}} ,\,\,\,{{q}_{2}} = \sqrt { - Q_{2}^{ + }} ,\,\,\,F = {{F}_{4}}. \hfill \\ \end{gathered} \right.$

Второе семейство – при учете соотношений:

(11)

$\left\{ \begin{gathered} {{Q}_{1}} \geqslant 0,\,\,\,Q_{2}^{ - } \geqslant 0{\text{:}}\,{{q}_{1}} = \sqrt {{{Q}_{1}}} ,\,\,\,{{q}_{2}} = \sqrt {Q_{2}^{ - }} ,\,\,\,F = {{F}_{1}}; \hfill \\ {{Q}_{1}} \geqslant 0,\,\,\,Q_{2}^{ - } < 0{\text{:}}\,{{q}_{1}} = \sqrt {{{Q}_{1}}} ,\,\,\,{{q}_{2}} = \sqrt { - Q_{2}^{ - }} ,\,\,\,F = {{F}_{2}}; \hfill \\ {{Q}_{1}} < 0,\,\,\,Q_{2}^{ - } \geqslant 0{\text{:}}\,{{q}_{1}} = \sqrt { - {{Q}_{1}}} ,\,\,\,{{q}_{2}} = \sqrt {Q_{2}^{ - }} ,\,\,\,F = {{F}_{3}}; \hfill \\ {{Q}_{1}} < 0,\,\,\,Q_{2}^{ - } < 0{\text{:}}\,{{q}_{1}} = \sqrt { - {{Q}_{1}}} ,\,\,\,{{q}_{2}} = \sqrt { - Q_{2}^{ - }} ,\,\,\,F = {{F}_{4}}. \hfill \\ \end{gathered} \right.$

Два семейства дисперсионных поверхностей соответствуют двум ветвям в спектре двухслойного графена (1). Первая и вторая строки в выражениях (10), (11) соответствуют состояниям, формируемым основным периодическим потенциалом, третья и четвертая строки – состояниям, возникающим за счет периодического расположения поверхностных (таммовских) состояний, формируемых на границе однослойного и двухслойного графена. С использованием квантовохимического моделирования методами теории функционала плотности показано, что в случае относительно узких полосок двухслойного графена по сравнению с периодом сверхрешетки (d_II$ \ll $ d) энергетический спектр рассматриваемой структуры можно считать симметричным относительно К-точки исходного материала (однослойного графена), и в этом случае низкоэнергетическое приближение, использованное для вывода дисперсионного уравнения, может считаться правомерным. Далее рассматривается именно такой случай: сверхрешетка состоит из широких полосок однослойного графена и узких полосок двухслойного.

Рассмотрим влияние параметра $\Delta $ на зонную структуру ГСР. На рис. 2 показаны графики решения дисперсионного уравнения при k_y = 0. Видно, что в случае Δ = 0 (рис. 2а) формируются две минизоны, каждая из которых дополнительно расщепляются на две подзоны, соответствующие решению уравнения (10) и (11). В случае, когда Δ отлично от нуля, первый положительный корень уравнения (11) при малых значениях k_x переносится в область значений энергии, соответствующих второй минизоне, а первая минизона не формируется, энергетическая поверхность терпит разрыв первого рода.

Рис. 2.

Зависимость энергии ε(q_x), q_y = 0 для двух нижних минизон, соответствующих зоне проводимости: Δ = 0 (а); Δ = 0.08t_⊥ (б). Cплошные линии соответствуют решению дисперсионного уравнения (10), пунктирные линии – решению уравнения (11). Энергия измеряется в единицах t_⊥.

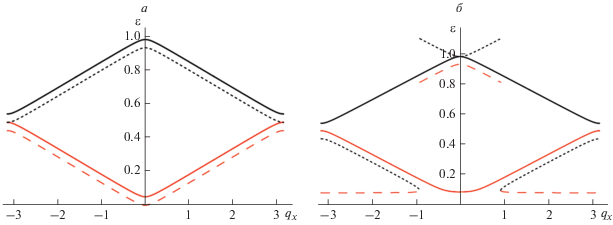
Следует отметить, что квантовохимическое моделирование, проведенное в [4], не показало существование расщепления минизон. Более того, при моделировании установлено, что энергетическая щель в спектре сверхрешетки возникает и в отсутствие постоянного электрического поля. Наличие дополнительных полосок графена, расположенных над поверхностью основного графенового листа, приводит к нарушению симметрии в спектре этого материала и к открытию энергетической щели. При этом из двух состояний, предсказываемых моделью Кронига–Пенни, реализуется одно – описываемое решением дисперсионного уравнения (10).

Параметр Δ – полуширина запрещенной зоны, формируемой в двухслойном графене при воздействии постоянного электрического поля, перпендикулярного поверхности образца. Меняя этот параметр, мы меняем и ширину запрещенной зоны, исследуемой СР, т.е. появляется возможность строить на основе такого материала измеритель частоты, работающий в терагерцевом диапазоне, основанный на эффекте межзонного поглощения. На рис. 3 приведены графики ε(q_x) при q_y = 0 и ε(q_y) при q_x = 0 в самой нижней минизоне, описываемой дисперсионным уравнением (10) при разных значениях Δ. Из графиков видно, что изменение параметра Δ влияет на форму дисперсионных поверхностей вблизи дна минизоны проводимости, с ростом $\left| {\vec {q}} \right|$ зависимость ε(q_x), ε(q_y) близка к линейной. Значение Δ является оценкой снизу для полуширины запрещенной зоны в энергетическом спектре рассматриваемой структуры. По q_x минизона, как и должно быть, конечна, но, как видно из графиков, ширина минизоны оказывается почти на порядок больше ширины запрещенной зоны. Полагая Δ = 0.1, t_⊥ = 0.04 эВ и приравнивая 2Δ = kT, получаем T ≈ 90 K – характерная температура, при которой в минизоне проводимости начнут появляться носители заряда вследствие теплового движения. Следовательно, при температурах порядка нескольких десятков кельвинов можно ожидать проявления эффекта межзонного поглощения света, носящего пороговый характер.

Рис. 3.

Зависимость энергии электрона ε от компонент квазиимпульса q_x, q_y в нижней минизоне, описываемой дисперсионным уравнением (10); (а) ε(q_x) при q_y = 0; (б) ε(q_y) при q_x = 0; 1 – Δ = 0.02t_⊥, 2 – Δ = 0.06t_⊥, 3 – Δ = 0.08t_⊥. Энергия измеряется в единицах t_⊥.

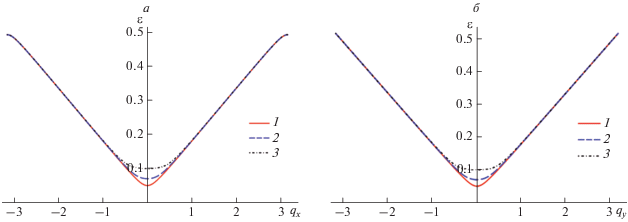
Поскольку ширина минизоны проводимости оказывается значительно больше ширины запрещенной зоны, и учет состояний вблизи потолка минизоны проводимости не столь важен при исследовании эффекта межзонного поглощения, энергетический спектр рассматриваемой структуры будем аппроксимировать моделью Кейна [14, 15]:

(12)

$\varepsilon = \sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}\left( {p_{x}^{2} + p_{y}^{2}} \right)} .$

Это выражение приближенно описывает спектр графена на подложке из карбида кремния [16, 17] или нитрида бора [18], в спектре которого присутствует энергетическая щель. Параметр υ₀ в случае графена на подложке, благодаря взаимодействию с которой в его спектре формируется энергетическая щель, отождествляется со скоростью на поверхности Ферми υ_F. Воспользуемся несколько видоизмененным выражением для подбора параметров кейновского спектра:

(13)

$\varepsilon \left( {{{q}_{x}},{{q}_{y}}} \right) = {{\varepsilon }_{0}}\left( {\gamma + \sqrt {{{\Delta }^{{'2}}} + \left( {q_{x}^{2} + q_{y}^{2}} \right)} } \right).$

Подбор коэффициентов будем вести таким образом, чтобы значения исходной и приближенной функции были максимально близки вблизи дна минизоны. В табл. 1 приведены значения параметров модели (13), вычисленные для случаев Δ = 0.04t_⊥ и Δ = 0.08t_⊥.

Таблица 1.

Значения подгоночных параметров в модели кейновского спектра (13)

	ε₀, мэВ	Δ'	γ
Δ = 0.04t_⊥	62.3674	0.22072	0.149129
Δ = 0.08t_⊥	67.2993	0.518656	–0.0386933

Из табл. 1 видно, что можно подобрать коэффициенты таким образом, чтобы параметр γ был пренебрежимо мал по сравнению с параметром Δ'. Таким образом, гамильтониан, описывающий состояния электрона в рассматриваемой графеновой сверхрешетке, может быть представлен в следующем виде:

(14)

$H\left( {\vec {p}} \right) = \left( {\begin{array}{*{20}{c}} {{{\Delta }_{0}}}&{{{\upsilon }_{0}}\left( {{{p}_{x}} - i{{p}_{y}}} \right)} \\ {{{\upsilon }_{0}}\left( {{{p}_{x}} + i{{p}_{y}}} \right)}&{ - {{\Delta }_{0}}} \end{array}} \right).$

Используя модель (12) для описания состояния электрона, мы фактически полагаем валентную зону и зону проводимости симметричными относительно значения энергии ε = 0. Гамильтониан (14) описывает две зоны, волновая функция электрона имеет вид:

(15)

$\begin{gathered} {{\psi }_{0}} = \frac{1}{L}\frac{{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} }}{{\sqrt {{{{\left( {\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} \pm {{\Delta }_{0}}} \right)}}^{2}} + \upsilon _{0}^{2}{{p}^{2}}} }} \times \\ \times \,\,{{\left( {1;\frac{{{{\upsilon }_{0}}\left( {{{p}_{x}} + i{{p}_{y}}} \right)}}{{{{\Delta }_{0}} \pm \sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} }}} \right)}^{T}}\exp \left( {\frac{{i{{p}_{x}}x}}{\hbar }} \right)~\exp \left( {\frac{{i{{p}_{y}}y}}{\hbar }} \right) \\ \end{gathered} $

энергия электрона в зоне проводимости

(16)

$\varepsilon = \pm \sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} .$

В выражениях (15), (16) знак “плюс” соответствует зоне проводимости, знак “минус” – валентной зоне, L² ‑ нормировочная площадь.

ВЫЧИСЛЕНИЕ ЭНЕРГИИ, ПОЛУЧАЕМОЙ ОБРАЗЦОМ, ЗА СЧЕТ МЕЖЗОННОГО ПОГЛОЩЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ

Рассмотрим эффект межзонного поглощения электромагнитной волны. Пусть на поверхность образца падает электромагнитная волна, плоскость поляризации которой направлена вдоль оси Х. Векторный потенциал высокочастотного поля положим равным

(17)

$\vec {A} = \left\{ {{{A}_{x}},{{A}_{y}}} \right\} = \left\{ { - \frac{{ic}}{\omega }{{E}_{m}}\exp \left( { - i\omega t} \right),0} \right\}.$

Выпишем уравнение Шрёдингера:

(18)

$i\hbar \frac{\partial }{{\partial t}}{\Psi } = H\left( {\vec {p} - \frac{e}{c}\vec {A}} \right){\Psi } = \left( {H\left( {\vec {p}} \right) + H{\kern 1pt} '\left( {\vec {A}} \right)} \right){\Psi ,}$

где оператор взаимодействия электрона с электромагнитным полем имеет вид

(19)

$H{\kern 1pt} ' = \left( {\begin{array}{*{20}{c}} 0&{{{\upsilon }_{0}}\frac{e}{c}{{A}_{x}}\left( t \right)} \\ {{{\upsilon }_{0}}\frac{e}{c}{{A}_{x}}\left( t \right)}&0 \end{array}} \right).$

Средняя энергия, получаемая материалом в единицу времени с единицы площади

(20)

$\begin{gathered} {{Q}_{{abs}}} = \frac{1}{{{{L}^{2}}}}\sum\limits_{l,\vec {p},l{\kern 1pt} ',\vec {p}{\kern 1pt} '} {W\left( {l,\vec {p},l{\kern 1pt} ',\vec {p}{\kern 1pt} '} \right)f\left( {l,\vec {p}} \right)} \times \\ \times \,\,\left( {1 - f\left( {l{\kern 1pt} ',\vec {p}{\kern 1pt} '} \right)} \right)\hbar \omega , \\ \end{gathered} $

где l, l' – номера зон, $\vec {p},\vec {p}{\kern 1pt} '$ – квазиимпульсы электрона в начальном и конечном состояниях, $W\left( {l,\vec {p},l{\kern 1pt} ',\vec {p}{\kern 1pt} '} \right)~$ – вероятность перехода, $f\left( {l,\vec {p}} \right)$ – функция распределения электронов. Поскольку влияние электромагнитной волны рассматривается как возмущение, в качестве функций $f\left( {l,\vec {p}} \right),$ $f\left( {l{\kern 1pt} ',\vec {p}{\kern 1pt} '} \right)$ возьмем равновесные функции Ферми–Дирака, полагая значение химического потенциала равным нулю. Вероятность перехода имеет вид:

(21)

$\begin{gathered} W\left( {l,\vec {p},l{\kern 1pt} ',\vec {p}{\kern 1pt} '} \right) = \frac{{2\pi }}{\hbar }{{\left| {\int {{\Psi *}} \left( {l{\kern 1pt} ',\vec {p}{\kern 1pt} '} \right)H{\kern 1pt} '{\Psi }\left( {l,\vec {p}} \right)d\vec {r}} \right|}^{2}} \times \\ \times \,\,\delta \left( {\varepsilon \left( {l{\kern 1pt} ',\vec {p}{\kern 1pt} '} \right) - \varepsilon \left( {l,\vec {p}} \right) - \hbar \omega } \right), \\ \end{gathered} $

где в качестве волновых функций возьмем собственные функции (15) невозмущенного гамильтониана кейновского спектра. Вычисляем матричный элемент перехода.

(22)

$\begin{gathered} \int {{\Psi }_{c}^{*}\left( {\vec {p}{\kern 1pt} '} \right)H{\kern 1pt} '{{{\Psi }}_{\upsilon }}\left( {\vec {p}} \right)d\vec {r}} = {{\delta }_{{\vec {p},\vec {p}{\kern 1pt} '}}}{{\upsilon }_{0}}\frac{e}{c}~{{A}_{x}}\left( t \right) \times \,\frac{{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{{'2}}}} + {{\Delta }_{0}}}}{{\sqrt {{{{\left( {\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{{'2}}}} + {{\Delta }_{0}}} \right)}}^{2}} + \upsilon _{0}^{2}{{p}^{{'2}}}} }}~ \times \\ \times \,\,\frac{{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} - {{\Delta }_{0}}}}{{\sqrt {{{{\left( {\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} - {{\Delta }_{0}}} \right)}}^{2}} + \upsilon _{0}^{2}{{p}^{2}}} }} \times \,\,\left( {\frac{{{{\upsilon }_{0}}\left( {{{p}_{x}} + i{{p}_{y}}} \right)}}{{{{\Delta }_{0}} - \sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} }} + \frac{{{{\upsilon }_{0}}\left( {p_{x}^{'} - ip_{y}^{'}} \right)}}{{{{\Delta }_{0}} + \sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{{'2}}}} }}} \right)~. \\ \end{gathered} $

Как и должно быть, возникает правило отбора, требующее равенства начального и конечного значения квазиимпульса электрона, характерное для процессов, обусловленных прямыми переходами. Таким образом, вероятность перехода имеет вид:

(23)

$\begin{gathered} W\left( {l,\vec {p},l{\kern 1pt} ',\vec {p}{\kern 1pt} '} \right) = \frac{{2\pi }}{\hbar }\frac{{{{e}^{2}}E_{m}^{2}}}{{{{\omega }^{2}}}}\upsilon _{0}^{2}\delta \left( {\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{{'2}}}} - } \right.\left. {\,\,\left( { - \sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} } \right) - \hbar \omega } \right){{\delta }_{{\vec {p},\vec {p}{\kern 1pt} '}}} \times \\ \times \,\,\left( {\frac{{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{{'2}}}} + {{\Delta }_{0}}}}{{\sqrt {{{{\left( {\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{{'2}}}} + {{\Delta }_{0}}} \right)}}^{2}} + \upsilon _{0}^{2}{{p}^{{'2}}}} }}} \right.\,\frac{{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} - {{\Delta }_{0}}}}{{\sqrt {{{{\left( {\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} - {{\Delta }_{0}}} \right)}}^{2}} + \upsilon _{0}^{2}{{p}^{2}}} }} \times \\ {{\left. { \times \,\,{\text{\;}}\left( {\frac{{{{\upsilon }_{0}}\left( {{{p}_{x}} + i{{p}_{y}}} \right)}}{{{{\Delta }_{0}} - \sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} }} + \frac{{{{\upsilon }_{0}}\left( {p_{x}^{{\text{'}}} - ip_{y}^{'}} \right)}}{{{{\Delta }_{0}} + \sqrt {\Delta _{0}^{2} + \nu _{0}^{2}{{p}^{{'2}}}} }}} \right)} \right)}^{2}}. \\ \end{gathered} $

Приведем выражение для средней энергии, получаемой материалом в единицу времени с единицы площади за счет межзонных переходов. Суммирование по $\vec {p}{\kern 1pt} '$ в (20) снимается, сумма по l, l' – сводится к одному слагаемому, соответствующему переходу электрона из валентной зоны в зону проводимости. После перехода от суммирования к интегрированию по $\vec {p}$ и записи интеграла по пространству квазиимпульсов в полярной системе координат получаем:

(24)

$\begin{gathered} {{Q}_{{abs}}} = \frac{{2\pi }}{\hbar }\frac{{{{e}^{2}}E_{m}^{2}}}{{{{\omega }^{2}}}}\frac{{\upsilon _{0}^{2}}}{2}\frac{{\hbar \omega }}{{{{{\left( {2\pi \hbar } \right)}}^{2}}}}\int\limits_{ - {\pi }}^{\pi } {d\varphi } \int\limits_0^\infty {pdp\delta } \times \\ \times \,\,\left( {2\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} - \hbar \omega } \right)\frac{{\exp {{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} } \mathord{\left/ {\vphantom {{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} } T}} \right. \kern-0em} T}~}}{{\left( {1 + \operatorname{ch} \left( {{{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} } \mathord{\left/ {\vphantom {{\sqrt {\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}} } T}} \right. \kern-0em} T}~} \right)} \right)}}\,\,\frac{{\Delta _{0}^{2} + {{{\left( {{{\upsilon }_{0}}p\sin \varphi ~} \right)}}^{2}}}}{{\Delta _{0}^{2} + \upsilon _{0}^{2}{{p}^{2}}}}. \\ \end{gathered} $

После вычисления интегралов получаем окончательно

(25)

${{Q}_{{abs}}} = \frac{1}{{8\hbar }}\frac{{{{e}^{2}}E_{m}^{2}}}{{{{{\left( {\hbar \omega } \right)}}^{2}}}}~\,\frac{{\exp \left( {\frac{{\hbar \omega }}{{2T}}} \right)}}{{1 + \operatorname{ch} \left( {\frac{{\hbar \omega }}{{2T}}} \right)}}\left( {\Delta _{0}^{2} + {{{\left( {\frac{{\hbar \omega }}{{2T}}} \right)}}^{2}}} \right)\,\theta \left( {\hbar \omega - 2{{\Delta }_{0}}} \right),$

где θ(x) – функция Хевисайда.

На единицу площади поверхности в единицу времени падает энергия

(26)

${{Q}_{0}} = \frac{{E_{m}^{2}}}{{2\pi }}c.$

Коэффициент поглощения α = Q_abs/Q₀,

(27)

$\begin{gathered} \alpha = \frac{{\pi {{e}^{2}}}}{{16\hbar c}}\,\,\frac{{\exp \left( {{{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {\left( {2T} \right)}}} \right. \kern-0em} {\left( {2T} \right)}}} \right)}}{{1 + \operatorname{ch} \left( {{{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {\left( {2T} \right)}}} \right. \kern-0em} {\left( {2T} \right)}}} \right)}}~\,\, \times \\ \times \,\,\left( {1 + \left( {\frac{{2{{\Delta }_{0}}}}{{\hbar \omega }}} \right)} \right)\theta \left( {\hbar \omega - 2{{\Delta }_{0}}} \right). \\ \end{gathered} $

На рис. 4 представлена зависимость коэффициента поглощения от частоты падающей волны при различных значениях полуширины запрещенной зоны.

Рис. 4.

Зависимость коэффициента поглощения α от частоты падающей волны ω при разных значениях полуширины запрещенной зоны Δ₀: 1 – Δ₀ = 0.04t_⊥; 2 – Δ₀ = 0.08t_⊥; 3 – Δ₀ = 0.12t_⊥. Температура T = 90 K.

ЗАКЛЮЧЕНИЕ

Исследована модель сверхрешетки, состоящей из чередующихся полосок однослойного и двухслойного графена, параметры энергетического спектра которой можно регулировать, меняя внешнее электрическое поле, перпендикулярное поверхности образца. На основе анализа дисперсионных уравнений, полученных в [4] при помощи модели Кронига–Пенни, показано, что энергетический спектр сверхрешетки, состоящей из чередующихся широких полосок однослойного и узких полосок двухслойного графена, может быть аппоксимирован кейновской моделью. Вычислен коэффициент поглощения света при межзонных переходах.

Работа выполнена при финансовой поддержке РФФИ и Администрации Волгоградской области в рамках научного проекта № 19-42-343006-р_мол_a.

Список литературы

Perenzoni M., Douglas J.P. Physics and applications of terahertz radiation. Springer, 2014. 255 p.
Nilsson J., Castro Neto A.H., Guinea F., Peres N.M.R. // Phys. Rev. B. 2008. V. 78. Art. No 045405.
Rozhkov A.V., Sboychakov A.O., Rakhmanov A.L., Nori F. // Phys. Rep. 2016. V. 648. P. 1.
Abdrakhmanov V.L., Badikova P.V., Zav’yalov D.V. et al. // arXiv: 2003.05696. 2020.
Dragoman D., Dragoman M., Plana R. // J. Appl. Phys. 2010. V. 107. Art. No 044312.
Dubey S., Singh V., Bhat A.K. et al. // Nano Lett. 2013. V. 13. Art. No 3990.
Forsythe C., Zhou X., Watanabe K. et al. // Nat. Nanotechnol. 2018. V. 13. P. 566.
Abdullah H.M., Zarenia M., Bahlouli H. et al. // EPL. 2016. V. 113. Art. No 17006.
Hoat D.M., Naseri M., Ponce-Perez R. et al // Superlatt. Microstruct. 2020. V. 137. Art No 106357.
Zhu L., Li L., Tao R. et al. // Nano Lett. 2020. V 20. V. 20. No 2. Art. No 1396.
Nakanishi T., Koshino M., Ando T. // Phys. Rev. B. 2010. V. 82. Art. No 125428.
Mirzakhani M., Zarenia M., Peeters F.M. // J. Appl. Phys. 2018. V. 123. Art. No 204301.
Fan X., Huang W., Ma T. et al. // EPL. 2015. V. 112. Art. No 58003.
Kane E.O. // J. Phys. Chem. Sol. 1957. V. 1. No 4. P. 249.
Chakraborty P.K., Choudhury S., Ghatak K.P. // Phys. B. 2007. V. 387. P. 333.
Bostwick A., Ohta T., McChesney J.L. et al. // New J. Phys. 2007. V. 9. P. 385.
Zhou S.Y., Gweon G.-H., Fedorov A.V. et al. // Nat. Mater. 2007. V. 6. P. 770.
Giovannetti G., Khomyakov P.A., Brocks G. et al. // Phys. Rev. B. 2007. V. 76. Art. No 073103.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал