Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 47-51

Математическое моделирование источника формирования фантомных изображений в виде РДС-кристалла: квантовые поляризационные характеристики с учетом дифракции

А. В. Белинский¹, Р. Сингх^1, *

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”, физический факультет
Москва, Россия

^* E-mail: ranjit.singh@mail.ru

Поступила в редакцию 20.07.2020
После доработки 28.08.2020
Принята к публикации 28.09.2020

DOI: 10.31857/S0367676521010051

Полный текст (PDF)

Аннотация

Рассмотрен процесс приготовления коррелированных многофотонных квантовых состояний с помощью кристаллов с регулярной доменной структурой и квадратичной нелинейностью. Получены пространственные и поляризационные характеристики формируемых коррелированных пучков. Рассчитаны статистические квантовые поляризационные операторы Стокса и межмодовые корреляционные коэффициенты.

ВВЕДЕНИЕ

Фантомные изображения [1] – один из вариантов решения проблемы изучения чувствительных к свету объектов, прямое оптическое наблюдение которых затруднено. Для формирования фантомных изображений необходим источник коррелированных световых пучков, один из которых взаимодействует с объектом, а другие – нет (см. рис. 1). При этом в объектном канале детектор дает информацию только о полной интенсивности прошедшего излучения. Сопряженные пучки не взаимодействует с объектом, но регистрируются ПЗС-матрицами, допуская измерение пространственной корреляционной функции интенсивности между каналами.

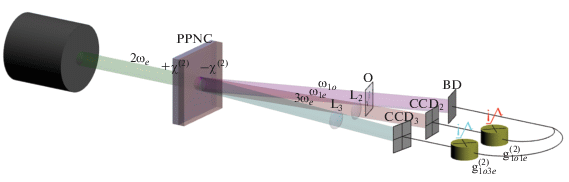
Рис. 1.

Схема формирования фантомных изображений: PPNC – нелинейный кристалл с регулярно-доменной структурой (РДС); $2{{\omega }_{e}}$ – накачка; ${{\omega }_{{1o}}},$ ${{\omega }_{{1e}}}$ и $3{{\omega }_{e}}$ – пучки коррелированных фотонов; O – объект; BD – интегрирующий детектор в объектном канале; L – оптические объективы; CCD – ПЗС матрица фотодетекторов в восстанавливающем канале; g – коррелятор интенсивностей (схема совпадений).

Одним из важных доводов в пользу использования квантовых фантомных изображений является создание максимально щадящих условий освещения исследуемого объекта, когда воздействие излучения на объект (иногда необратимое) минимально [2]. Особенно это важно при облучении живых существ, например, рентгеновским излучением.

Дополнительным источником информации при изучении исследуемых объектов может быть состояние поляризации отраженного или рассеянного ими излучения. В этом случае можно говорить о поляризационно-ориентированных фантомных изображениях. Определенные успехи в этом направлении уже имеются [3]. Однако оценить качество формируемых изображений можно лишь с учетом дифракции.

Кроме того, важно знать пространственное распределение формируемых источником коррелированных пучков, поскольку неравномерное освещение объекта приведет к систематическим ошибкам его измерения, которые необходимо должны быть учтены при последующей компьютерной обработке.

Все эти причины послужили поводом к проведению исследований, приведших к написанию этой статьи. При этом мы рассмотрели весьма перспективный в отношении формирования фантомных изображений источник виде РДС кристалла [4–9].

ПРОСТРАНСТВЕННОЕ РАСПРЕДЕЛЕНИЕ ИЗЛУЧЕНИЯ ПОЛЯРИЗОВАННЫХ ПУЧКОВ

Рассмотрим 4 монохроматические моды с кратными частотами, характеризуемые операторами уничтожения фотона, которые коллинеарно распространяются внутри регулярно-доменного кристалла с квадратичной нелинейностью. Операторы удовлетворяют стандартным коммутационным соотношениям [5–7]: $\left[ {{{{\hat {A}}}_{{jp}}}\left( {\vec {r},z} \right),\hat {A}_{{j{\kern 1pt} 'p{\kern 1pt} '}}^{ + }\left( {\vec {r}{\kern 1pt} ',z{\kern 1pt} '} \right)} \right]$ = $ = {{\delta }_{{jp,j{\kern 1pt} 'p{\kern 1pt} '}}}\left( {\vec {r} - \vec {r}{\kern 1pt} '} \right){{\delta }_{{jp,j{\kern 1pt} 'p{\kern 1pt} '}}}\left( {z - z{\kern 1pt} '} \right),$ $j = 1,2,3;$ $p,p{\kern 1pt} ' = o$ – обыкновенная волна; $p,p' = e$ – необыкновенная волна; $\vec {r} = \left( {x,y} \right)$ – поперечные координаты и $z$ – продольное направление распространения пучков.

Одновременно происходят два процесса: параметрическая генерация субгармоник (тип II) и преобразование частоты вверх за счет суммирования частот субгармоник с частотой накачки:

(1)

$\begin{gathered} 2{{\omega }_{e}} = {{\omega }_{o}} + {{\omega }_{e}},\,\,\,\,~\delta {{k}_{1}} = {{k}_{{2e}}} - {{k}_{{1o}}} - {{k}_{{1e}}} + \\ + \,\,{{m}_{1}}{{G}_{1}} = \Delta {{k}_{1}} + {{m}_{1}}{{G}_{1}}, \\ \end{gathered} $

(2)

$\begin{gathered} {{\omega }_{o}} + 2{{\omega }_{e}} = 3{{\omega }_{e}},\,\,\,\,~\delta {{k}_{2}} = {{k}_{{3e}}} - {{k}_{{1o}}} - {{k}_{{2e}}} + \\ + \,\,{{m}_{2}}{{G}_{2}} = \Delta {{k}_{2}} + {{m}_{2}}{{G}_{2}}, \\ \end{gathered} $

где ${{k}_{{jp}}}$ – абсолютные значения волновых векторов соответствующих мод с частотами ${{\omega }_{{jp}}};$ $j = 1,2,3;$ $\Delta {{k}_{q}}$ – волновые расстройки соответствующего процесса для однородного кристалла; $q = 1,2;$ ${{m}_{q}} = \pm 1,\,\, \pm {\kern 1pt} 3,\,\, \pm {\kern 1pt} 5,\,\, \ldots $ – порядки квазисинхронизма; ${{G}_{q}} = \frac{{2\pi }}{{{{\Lambda }_{q}}}}$ – волновое число – модуль “псевдовектора” решетки доменной структуры с периодом ${{\Lambda }_{q}}$ [5, 6, 10–13].

Система операторных уравнений этих процессов имеет следующий вид [5–7, 10, 12, 13]:

(3)

$\left\{ \begin{gathered} \left( {\frac{\partial }{{\partial z}} - \frac{i}{{2{{k}_{{1oz}}}}}{{\Delta }_{ \bot }}} \right)\hat {A}_{{1o}}^{ + }\left( {\vec {r},z} \right) = \hfill \\ = i{{\gamma }_{1}}{{{\hat {A}}}_{{1e}}}\left( {\vec {r},z} \right) + i{{\gamma }_{2}}\hat {A}_{{3e}}^{ + }\left( {\vec {r},z} \right), \hfill \\ \left( {\frac{\partial }{{\partial z}} + \frac{i}{{2{{k}_{{1ez}}}}}{{\Delta }_{ \bot }}} \right){{{\hat {A}}}_{{1e}}}\left( {\vec {r},z} \right) = - i{{\gamma }_{1}}\hat {A}_{{1o}}^{ + }\left( {\vec {r},z} \right), \hfill \\ \left( {\frac{\partial }{{\partial z}} - \frac{i}{{2{{k}_{{3ez}}}}}{{\Delta }_{ \bot }}} \right)\hat {A}_{{3e}}^{ + }\left( {\vec {r},z} \right) = i{{\gamma }_{2}}\hat {A}_{{1o}}^{ + }\left( {\vec {r},z} \right), \hfill \\ \end{gathered} \right.$

где ${{\Delta }_{ \bot }} = {{\Delta }_{ \bot }}\left( {x,y} \right)$ – поперечный лапласиан; нелинейные коэффициенты связи: ${{\gamma }_{1}},$ ${{\gamma }_{2}}$ отвечают за параметрический процесс (1) и преобразование частоты вверх (2), соответственно; Амплитуда моды накачки $2e$ является плоской неистощимой. При этом мы выбрали приближение заданной накачки, чтобы получить и проанализировать аналитическое решение.

Линейную систему операторных уравнений (3) подвергнем преобразованию Фурье по переменным $x,y{\text{:}}$

(4)

$\left\{ \begin{gathered} \left( {\frac{\partial }{{\partial z}} + i{{q}_{{1o}}}} \right)\hat {a}_{{1o}}^{ + }\left( {{{{\vec {k}}}_{{1o}}},z} \right) = \hfill \\ = i{{\gamma }_{1}}{{{\hat {a}}}_{{1e}}}\left( {{{{\vec {k}}}_{{1e}}},z} \right) + i{{\gamma }_{2}}\hat {a}_{{3e}}^{ + }\left( {{{{\vec {k}}}_{{3e}}},z} \right), \hfill \\ \left( {\frac{\partial }{{\partial z}} - i{{q}_{{1e}}}} \right){{{\hat {a}}}_{{1e}}}\left( {{{{\vec {k}}}_{{1e}}},z} \right) = - i{{\gamma }_{1}}\hat {a}_{{1o}}^{ + }\left( {{{{\vec {k}}}_{{1o}}},z} \right), \hfill \\ \left( {\frac{\partial }{{\partial z}} + i{{q}_{{3e}}}} \right)\hat {a}_{{3e}}^{ + }\left( {{{{\vec {k}}}_{{3e}}},z} \right) = i{{\gamma }_{2}}\hat {a}_{{1o}}^{ + }\left( {{{{\vec {k}}}_{{1o}}},z} \right), \hfill \\ \end{gathered} \right.$

где ${{q}_{{jp}}} = \frac{{k_{{jpx}}^{2} + k_{{jpy}}^{2}}}{{2{{k}_{{jpz}}}}},$ ${{\vec {k}}_{{jp}}} = \left( {{{k}_{{jpx}}},{{k}_{{jpy}}}} \right)$ и ${{\hat {a}}_{{jp}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right)$ = $ = \frac{1}{{{{{\left( {\sqrt {2\pi } } \right)}}^{2}}}}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {{{{\hat {A}}}_{{jp}}}\left( {x,y,z} \right)} } $ × ${{e}^{{ - i\left( {{{k}_{{jpx}}}x + {{k}_{{jpy}}}y} \right)}}}dxdy,$

(5)

${{\hat {a}}_{{jp}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) = Q\left( {{{{\vec {k}}}_{{jp}}},z} \right){{\hat {a}}_{{jp}}}\left( 0 \right).$

Здесь ${{\hat {a}}_{{jp}}} = {{\left( {\hat {a}_{{1o}}^{ + },{{{\hat {a}}}_{{1e}}},\hat {a}_{{3e}}^{ + }} \right)}^{T}};$ T – знак транспонирования; $Q\left( {{{{\vec {k}}}_{{jp}}},z} \right)$ – передаточная функция в виде матрицы коэффициентов размера 3 × 3, которые рассчитаны численно.

Правильность выкладок проверяется контролем коммутационных соотношений, которые сводятся к виду:

$\begin{gathered} {{Q}_{{11}}}Q_{{11}}^{*} - {{Q}_{{12}}}Q_{{12}}^{*} + {{Q}_{{13}}}Q_{{13}}^{*} = 1, \\ - {{Q}_{{21}}}Q_{{21}}^{*} + {{Q}_{{22}}}Q_{{22}}^{*} - {{Q}_{{23}}}Q_{{23}}^{*} = 1, \\ {{Q}_{{31}}}Q_{{31}}^{*} - {{Q}_{{32}}}Q_{{32}}^{*} + {{Q}_{{33}}}Q_{{33}}^{*} = 1, \\ \end{gathered} $

которые, разумеется, выполняются.

КВАНТОВЫЕ СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛЯРИЗАЦИИ МОД

Для изучения динамики среднего числа фотонов, в том числе поляризационных характеристик ортогональных мод $1o$ и $1e,$ вычислим, как это принято, следующие величины:

средние числа фотонов

(6)

${{\hat {N}}_{{jp}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) = \hat {a}_{{jp}}^{ + }\left( {{{{\vec {k}}}_{{jp}}},z} \right){{\hat {a}}_{{jp}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right),$

коэффициенты корреляции фотонов между модами

(7)

$\begin{gathered} \hat {g}_{{jp,j{\kern 1pt} 'p{\kern 1pt} '}}^{{\left( 2 \right)}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) = \\ = \frac{{\hat {a}_{{jp}}^{ + }\left( {{{{\vec {k}}}_{{jp}}},z} \right){{{\hat {a}}}_{{jp}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right)\hat {a}_{{j{\kern 1pt} 'p{\kern 1pt} '}}^{ + }\left( {{{{\vec {k}}}_{{j{\kern 1pt} 'p{\kern 1pt} '}}},z} \right){{{\hat {a}}}_{{j{\kern 1pt} 'p{\kern 1pt} '}}}\left( {{{{\vec {k}}}_{{j{\kern 1pt} 'p{\kern 1pt} '}}},z} \right)}}{{{{{\hat {N}}}_{{jp}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right){{{\hat {N}}}_{{j{\kern 1pt} 'p{\kern 1pt} '}}}\left( {{{{\vec {k}}}_{{j{\kern 1pt} 'p{\kern 1pt} '}}},z} \right)}}, \\ \end{gathered} $

средние значения операторов Стокса

(8)

$\begin{gathered} {{{\hat {S}}}_{{0,1}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) = \hat {a}_{{1o}}^{ + }\left( {{{{\vec {k}}}_{{jp}}},z} \right){{{\hat {a}}}_{{1o}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) \pm \\ \pm \,\,\hat {a}_{{1e}}^{ + }\left( {{{{\vec {k}}}_{{jp}}},z} \right){{{\hat {a}}}_{{1e}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right), \\ \end{gathered} $

(9)

$\begin{gathered} {{{\hat {S}}}_{2}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) = \hat {a}_{{1o}}^{ + }\left( {{{{\vec {k}}}_{{jp}}},z} \right){{{\hat {a}}}_{{1e}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) + \\ + \,\,\hat {a}_{{1e}}^{ + }\left( {{{{\vec {k}}}_{{jp}}},z} \right){{{\hat {a}}}_{{1o}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right), \\ \end{gathered} $

(10)

$\begin{gathered} {{{\hat {S}}}_{3}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) = i\hat {a}_{{1e}}^{ + }\left( {{{{\vec {k}}}_{{jp}}},z} \right){{{\hat {a}}}_{{1o}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right) - \\ - \,\,i\hat {a}_{{1o}}^{ + }\left( {{{{\vec {k}}}_{{jp}}},z} \right){{{\hat {a}}}_{{1e}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right), \\ \end{gathered} $

степени поляризации взаимодействующих ортогональных мод

(11)

$d\left( {{{{\vec {k}}}_{{jp}}},z} \right) = \frac{{\sqrt {{{{\hat {S}}}_{1}}{{{\left( {{{{\vec {k}}}_{{jp}}},z} \right)}}^{2}} + {{{\hat {S}}}_{2}}{{{\left( {{{{\vec {k}}}_{{jp}}},z} \right)}}^{2}} + {{{\hat {S}}}_{3}}{{{\left( {{{{\vec {k}}}_{{jp}}},z} \right)}}^{2}}} }}{{{{{\hat {S}}}_{0}}\left( {{{{\vec {k}}}_{{jp}}},z} \right)}}.$

Усреднение операторов (6)–(11) будем производить для вакуумного начального состояния мод $1o,$ $1e$ и $3e.$ Результаты представлены на рис. 2–4 .

Рис. 2.

Динамика значений среднего числа фотонов в моде $1o$ в случае, когда накачка моды 2e неистощимая, а остальные моды находятся в начальном вакуумном состоянии. Цифры над контурными линиями показывают значения ${{N}_{{1o}}}.$ При этом остальные коэффициенты имеют следующие значения: ${{q}_{{1e}}} = 1,$ ${{q}_{{3e}}} = 1,$ ${{\gamma }_{1}} = 1$ и ${{\gamma }_{2}} = 0.5.$ Поведение остальных мод 1e и 3e аналогично.

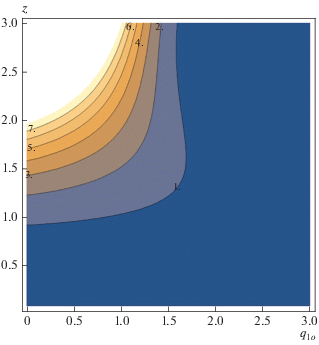
Рис. 3.

Динамика значений коэффициента корреляции мод 1o и 1e для тех же параметров, что и на рис. 2. Цифры над контурными линиями показывают значения ${{g}_{{1o1e}}}.$ Поведение коэффициента корреляции ${{g}_{{1e3e}}}$ мод 1e и 3e аналогично, а ${{g}_{{1o3e}}} = 2.$

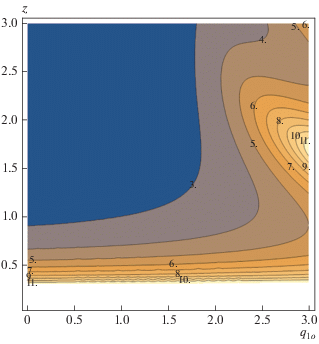
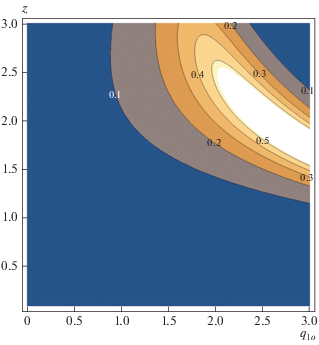
Рис. 4.

Динамика значений степени поляризации между модами 1o и 1e для тех же исходных параметров, что и на рис. 2, 3 . Цифры над контурными линиями показывают значения d.

Операторы (8)–(10) удовлетворяют следующим коммутационным соотношениям:

$\begin{gathered} \left[ {{{{\hat {S}}}_{0}}\left( {{{{\vec {k}}}_{{jp}}},z} \right),{{{\hat {S}}}_{{1,2,3}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right)} \right] = 0, \\ ~\left[ {{{{\hat {S}}}_{{1,2,3}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right),{{{\hat {S}}}_{{2,3,1}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right)} \right] = 2i{{{\hat {S}}}_{{3,1,2}}}\left( {{{{\vec {k}}}_{{jp}}},z} \right). \\ \end{gathered} $

Соотношение неопределенности для операторов Стокса имеет вид:

$\begin{gathered} \left\langle {\Delta S_{j}^{2}\left( {{{{\vec {k}}}_{{jp}}},z} \right)} \right\rangle \left\langle {\Delta S_{k}^{2}\left( {{{{\vec {k}}}_{{jp}}},z} \right)} \right\rangle \geqslant {{\left| {{{S}_{l}}\left( {{{{\vec {k}}}_{{jp}}},z} \right)} \right|}^{2}}, \\ \left( {j \ne k \ne l} \right). \\ \end{gathered} $

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА

Результаты расчетов приведены на рис. 2–4 . Они необходимы для оценки пригодности и перспектив использования РДС-кристаллов в качестве источников коррелированного оптического излучения при формировании фантомных изображений. Полученные значения корреляционных коэффициентов 2-го порядка между фотонами ортогональных поляризационных мод $1o$ и $1e$ не только дают потенциальную возможность успешно сформировать изображение, но также позволяют изучить и восстановить степень поляризации $d\left( {{{{\vec {k}}}_{{jp}}},z} \right)$ поступающего от объекта света (см. рис. 4). Это несомненно открывает новые перспективы построения и оптимизации схем формирования фантомных изображений.

Кроме того, моделирование пространственной конфигурации коррелированных световых пучков дает аргументированные оценки качества формируемых изображений, их пространственного разрешения и неоднородности освещения, что также важно с точки зрения точности измерений.

Работа выполнена при поддержке РФФИ (проект № 18-01-00598а).

Список литературы

Колобов М.И., Чиркин А.С. Квантовое изображение М.: Физматлит, 2009.
Basset M.G., Setzpfandt F., Steinlechner F. et al. // Laser Photon. Rev. 2019. V. 13. No 10. Art. No 1900097.
Balakin D.A., Belinsky A.V., Chirkin A.S. // Quant. Inf. Proc. 2019. V. 18. Art. No 80.
Chirkin A.S., Gostev P.P., Agapov D.P. et al. // Laser Phys. Lett. 2018. V. 15. No 11. Art. No 115404.
Chirkin A.S., Makeev E.V. // J. Mod. Opt. 2006. V. 53. No 5–6. P. 821.
Chirkin A.S., Makeev E.V. // J. Opt. B. 2005. V. 7. S500.
Morozov E.Yu., Chirkin A.S. // J. Opt. A. 2003. V. 5. P. 233.
Родионов А.В., Чиркин А.С. // Опт. и спектроск. 2004. Т. 96. № 5. С. 790; Rodionov A.V., Chirkin A.S. // Opt. Spectrosс. 2004. V. 96. No 5. P. 721.
Чиркин А.С. // Квант. электрон. 2000. Т. 30. № 10. С. 847; Chirkin A.S. // Quant. Electron. 2000. V. 30. No 10. P. 847.
Dmitriev V.G., Singh R. // Int. J. Quant. Inform. 2003. V. 1. No 3. P. 403.
Белинский А.В., Сингх Р. // Квант. электрон. 2018. Т. 48. № 7. С. 611; Belinsky A.V., Singh R. // Quant. Electron. 2018. V. 48. No 7. P. 611.
Белинский А.В., Сингх Р. // Изв. РАН. Сер. физ. 2020. Т. 84. № 3. С. 382.
Белинский А.В., Сингх Р. // Изв. РАН. Сер. физ. 2020. Т. 84. № 1. С. 137; Belinsky A.V., Singh R. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No 1. P. 107.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал