1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 1, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 28-33

Оптические вихри в квадратично-нелинейных средах при нелинейном поглощении

Б. С. Брянцев 1, *, А. А. Калинович 1, И. Г. Захарова 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

* E-mail: brisbryantsev@mail.ru

Поступила в редакцию 20.07.2020
После доработки 28.08.2020
Принята к публикации 28.09.2020

Полный текст (PDF)

Аннотация

Исследовано распространение оптических вихрей в квадратично-нелинейных средах при наличии линейного и нелинейного поглощения. Известно, что при распространении таких пучков в средах с квадратичной нелинейностью без поглощения вихревая структура пучка разрушается и пучок распадается на несколько невихревых квази-солитонов. Показано, что нелинейное поглощение позволяет пучку дольше сохранять свою структуру.

ВВЕДЕНИЕ

Световые пучки с фазовыми особенностями много десятилетий изучаются в нелинейной оптике. Однако, наблюдать в эксперименте образование устойчивых многомерных вихревых солитонов очень сложно. Известно, что в консервативных однородных нелинейных средах азимутальная неустойчивость является характерной особенностью вихрей [1, 2]. За последние двадцать лет появилось большое количество работ, исследующих различные механизмы, которые могли бы сохранить вихревую структуру и повысить устойчивость многомерных оптических солитонов с фазовыми сингулярностями. Основное внимание было сосредоточено на вихревых солитонах в средах с кубической нелинейностью. Например, устойчивость вихрей в среде с нелинейностью Керра показана при наличии дополнительного усиления, локализованного в кольцевой структуре [3]. Кроме того, наблюдались устойчивые вихри как для фокусирующей, так и для дефокусирующей нелинейности. Коллапса и азимутальной неустойчивости вихрей в среде с нелинейностью Керра можно избежать за счет нелокальности среды [4, 5]. В качестве примера нелокальной нелинейной среды, в которой экспериментально наблюдались устойчивые вихревые солитоны, следует упомянуть нематические жидкие кристаллы [6]. Неоднородность существенно изменяет характер распространения волны с фазовой сингулярностью. Выявлены устойчивые вихревые структуры в неоднородных средах с дефокусирующей кубической нелинейностью [7]. Стабильные оптические вихри также наблюдаются в фотонных решетках [8] и в структурах с PT-симметрией [9]. Параметрическое взаимодействие волн усложняет рассматриваемые процессы. В [10] рассматривают линейные и нелинейные волноводы, индуцированные парой вихрей с одинаковой частотой, но разной поляризацией.

Обзор современного состояния исследований оптических вихревых структур приведен в статьях [11–13]. В частности, в данных работах обсуждаются многомерные вихревые солитоны в диссипативных средах.

Наше исследование посвящено распространению пространственно-временных импульсных световых пучков при генерации второй гармоники. Такая задача может быть сведена к решению известной системы квазиоптических уравнений параболического типа. Аналогичные задачи решались аналитически путем обобщения известной комбинации метода усредненного Лагранжа и голографического метода [14–16]. В работе [17] рассматривается формирование параметрических солитонов с вихревой структурой при наличии таких физических эффектов, как волноводная структура, линейная и двухфотонная диссипация или усиление, а также дисперсия групповых скоростей. При квадратичной нелинейности вышеуказанные эффекты, как ожидается, будут способствовать образованию вихревых пространственно-временных солитонов – оптических пуль.

ПОСТАНОВКА ЗАДАЧИ

Мы описываем распространение электромагнитного импульса с использованием квазиоптического приближения в случае фазового синхронизма [15]. Безразмерные уравнения выглядят следующим образом:

(1)
$\begin{gathered} i\frac{{\partial {{A}_{1}}}}{{\partial z}} + {{D}_{{{\tau 1}}}}\frac{{\partial {{A}_{1}}}}{{\partial {{\tau }^{2}}}} = A_{1}^{{\text{*}}}{{A}_{2}} - i{{\alpha }_{{01}}}{{A}_{1}} - i{{\alpha }_{{11}}}{{\left| {{{A}_{1}}} \right|}^{2}}{{A}_{1}} + \\ + \,\,{{D}_{{q1}}}h\left( {x,y} \right) + {{D}_{1}}{{{\Delta }}_{ \bot }}{{A}_{1}}, \\ \end{gathered} $
(2)
$\begin{gathered} i\frac{{\partial {{A}_{2}}}}{{\partial z}} + {{D}_{{{\tau 2}}}}\frac{{\partial {{A}_{2}}}}{{\partial {{\tau }^{2}}}} = \gamma A_{1}^{2} - i{{\alpha }_{{02}}}{{A}_{2}} - i{{\alpha }_{{12}}}{{\left| {{{A}_{2}}} \right|}^{2}}{{A}_{2}} + \\ + \,\,{{D}_{{q2}}}h\left( {x,y} \right) + {{D}_{2}}{{{\Delta }}_{ \bot }}{{A}_{2}}, \\ \end{gathered} $
где A1,2 – безразмерные комплексные амплитуды огибающей импульса первой и t второй гармоник, x, y, z-безразмерные координаты, $\tau = t - {z \mathord{\left/ {\vphantom {z c}} \right. \kern-0em} c}$ – безразмерное локальное время, ${{D}_{{1,2}}},$ ${{D}_{{{\tau 1,2}}}},$ ${{D}_{{q1,2}}}$ – безразмерные коэффициенты дифракции, дисперсии и волновода соответственно, γ описывает нелинейность, ${{{\alpha }}_{{01}}},$ ${{{\alpha }}_{{02}}},$ ${{{\alpha }}_{{11}}},$ ${{{\alpha }}_{{12}}}$ соответствуют линейному и нелинейному поглощению $h\left( {x,y} \right)$ – безразмерная функция, описывающая поперечный профиль волновода. В настоящей работе в качестве потенциала гармонического осциллятора выбран профиль волновода $h\left( {x,y} \right)$ = $\left( {{{x}^{2}} + {{y}^{2}}} \right).$ Уравнения (1), (2) решаются численно с использованием консервативной нелинейной разностной схемы, реализуемой с помощью эффективного многоэтапного итерационного алгоритма [14].

На вход среды падает двухкомпонентный вихревой пучок-импульс:

(3)
${{\left. {{{A}_{{1,2}}}\left( {x,y,\tau } \right)} \right|}_{{z = 0}}} = {{A}_{{10,20}}}{\text{exp}}\left( {{{\rho }^{2}} + {{\tau }^{2}} + i{{\varphi }_{{1,2}}}} \right)\rho ,$
где ${{\rho }^{2}} = {{x}^{2}} + {{y}^{2}},$ ${{\varphi }_{1}} = {\text{arg}}\left( {x + iy} \right),$ ${{\varphi }_{2}} = 2{{\varphi }_{1}}$ и ${{A}_{{10,20}}}$ – константы, определяющие начальные амплитуды компонент.

Мы предполагаем, что, в частности, нелинейное поглощение может быть использовано для стабилизации вихревого солитона. В этом случае возникающие возмущения вихревой структуры, имеющие большую амплитуду, сильно затухают. В результате разрушение вихревого солитона должно происходить на большем расстоянии вдоль продольной координаты z.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

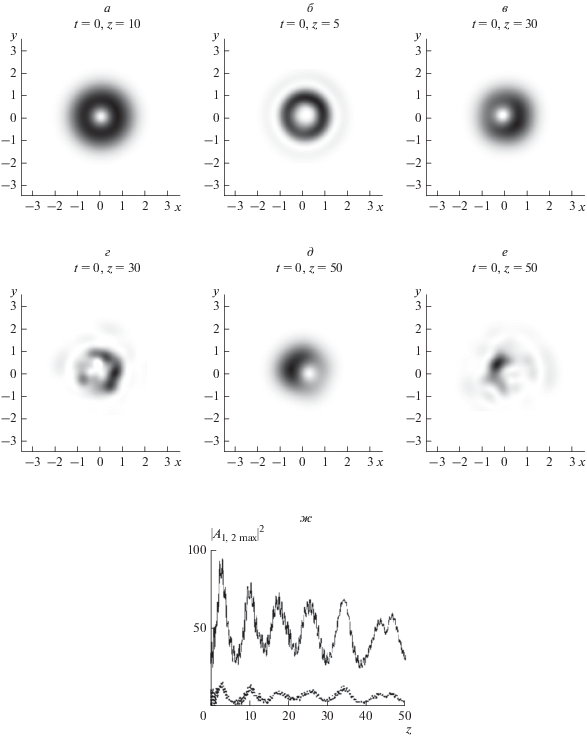
Была проведена серия численных расчетов для проверки наших предположений. На рис. 1 показано распределение амплитуды и фазы на разных расстояниях при отсутствии линейного и нелинейного поглощения α01 = α02 = 0, α11 = α12 = 0. Были использованы следующие параметры: ${{A}_{{10}}} = 15,$ ${{A}_{{20}}} = 0,$ ${{D}_{1}} = 1.0,$ ${{D}_{2}} = 0.5,$ ${{D}_{{{\tau 1}}}} = 0.05,$ ${{D}_{{{\tau 1}}}} = 0.1,$ ${{D}_{{q1}}} = - 10,$ ${{D}_{{q2}}} = - 10.$ На входе подается пучок основной частоты, который генерирует вторую гармонику и образуется двухцветный вихревой солитон. Как известно, такие солитоны нестабильны и при распространении распадаются на несколько невихревых квази-солитонов. Пучок начинает терять вихревую структуру и превращаться в невихревой солитон уже при $z = 30.$ При $z = 50$ вихревая структура у него практически отсутствует.

Рис. 1.

Распределения амплитуды основной частоты (а, в, д) и второй гармоники (б, г, е) на расстоянии $z = 10$ (а, б), $z = 30$ (в, г), $z = 50$ (д, е) и зависимость пиковых интенсивностей основной (сплошная) и второй (пунктирная) гармоник (ж) при отсутствии линейного и нелинейного поглощения. Параметры: α01 = α02 = 0.0, α11 = α12 = 0.0. ${{A}_{{10}}} = 15,$ ${{A}_{{20}}} = 0,$ ${{D}_{1}} = 1.0,$ ${{D}_{2}} = 0.5,$ ${{D}_{{{\tau 1}}}} = 0.05,$ ${{D}_{{{\tau 1}}}} = 0.1,$ ${{D}_{{q1}}} = - 10,$ ${{D}_{{q2}}} = - 10.$

На рис. 2 показано распространение такого пучка при наличии линейного поглощения, α01 = α02 = 0.1, α11 = α12 = 0, остальные параметры совпадают с величинами, указанными в предыдущем случае. При этом на основной частоте вихревая структура сохраняется на всей трассе, на второй гармонике структура искажена, но в целом имеет вихревой вид. На графике пиковой интенсивности (рис. 2д) видно, что интенсивность пучка резко падает уже к $z = 10,$ т.е. распространяется уже не солитонный пучок, а два практически не связанных между собой пучка на основной частоте и второй гармонике. Из этого можно сделать вывод, что линейное поглощение мало подходит для стабилизации вихревых солитонов, а способствует только сохранению вихревой структуры пучка.

Рис. 2.

Распределения амплитуды основной частоты (а, в) и второй гармоники (б, г) на расстоянии $z = 30$ (а, б), $z = 50$ (в, г) и зависимость пиковых интенсивностей основной (сплошная) и второй (пунктирная) гармоник (д) при линейном поглощении. Параметры: α01 = α02 = 0.1, α11 = α12 = 0.0. ${{A}_{{10}}} = 15,$ ${{A}_{{20}}} = 0,$ ${{D}_{1}} = 1.0,$ ${{D}_{2}} = 0.5,$ ${{D}_{{{\tau 1}}}} = 0.05,$ ${{D}_{{{\tau 1}}}} = 0.1,$ ${{D}_{{q1}}} = - 10,$ ${{D}_{{q2}}} = - 10.$

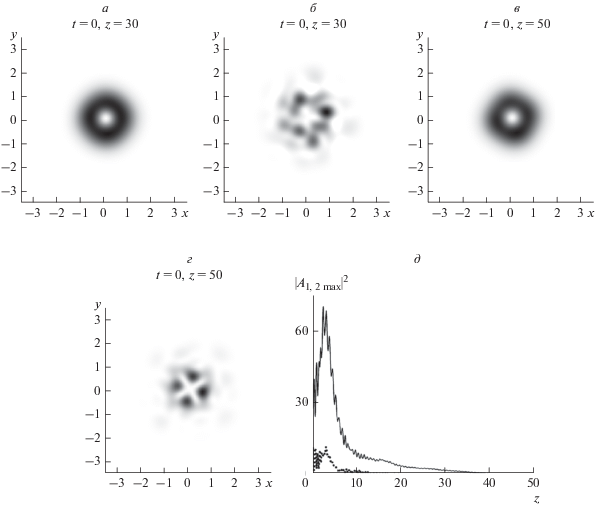
Нелинейное поглощение более выражено в областях с максимальной интенсивностью. В связи с этим мы ожидаем, что с его помощью можно предотвратить распад на отдельные солитоны, поскольку формирующиеся участки с максимальной интенсивностью будут поглощаться сильнее. В реальных средах нелинейное поглощение обычно связано с линейным, поэтому учтем оба фактора. На рис. 3 показано распределение амплитуды и фазы при α01 = α02 = 0.01, α11 = α12 = 0.5. В этом случае можно сказать, что вихревая структура пучка все еще сохраняется на трассе $z = 30.$ Даже при $z = 50$ вихревая структура частично наблюдается. Пиковая интенсивность пучка приведена на рис. 3д. В начале пучок за счет нелинейного поглощения резко теряет интенсивность, но начиная с $z = 10,$ можно говорить о стабилизации пучка, распространяющегося как связанное состояние. Таким образом, можно сделать вывод, что нелинейное поглощение способствует устойчивости вихревых пучков.

Рис. 3.

Рисунок построен аналогично рис. 2. Случай линейного и нелинейного поглощения при α01 = α02 = 0.01, α11 = = α12 = 0.5. На зависимости пиковых интенсивностей (д) сделана врезка области $z > 10$ в увеличенном масштабе.

ЗАКЛЮЧЕНИЕ

В работе рассмотрено распространение оптического вихря в квадратично-нелинейном волноводе при наличии линейного и нелинейного поглощения. С помощью численного моделирования показано, что поглощение позволяет пучку дольше сохранять вихревую структуру, предотвращая распад пучка на несколько невихревых квази-солитонов. Нелинейное поглощение более эффективно, чем линейное удерживает пучок от распада за счет того, что наиболее интенсивно поглощаются области с максимальной интенсивностью.

Исследование выполнено при поддержке Российского научного фонда (проект № 17-11-01157).

Список литературы

  1. Kivshar Yu.S., Agrawal G.P. Optical solitons: from fibers to photonic crystals. Amsterdam: Academic Press, 2003. 540 p.

  2. Desyatnikov A.S., Torner L., Kivshar Yu. // Progr. Opt. 2005. V. 47. P. 291.

  3. Huang C., Ye F., Malomed B.A. et al. // Opt. Lett. 2013. V. 38. No 13. P. 2177.

  4. Kartashov Y.V., Vysloukh V.A., Torner L. // Opt. Expr. 2007. V. 15. No 15. P. 9378.

  5. Ye F., Kartashov Y.V., Hu B. et al. // Opt. Lett. 2010. V. 35. No 5. P. 628.

  6. Izdebskaya Y., Assanto G., Krolikowski W. // Opt. Lett. 2015. V. 40. No 17. P. 4182.

  7. Kartashov Y.V., Malomed B.A., Vysloukh V.A. et al. // Opt. Lett. 2017. V. 42. No 3. P. 446.

  8. Yao X., Liu X. // Opt. Lett. 2018. V. 43. No 23. P. 5749.

  9. Huang C., Dong L. // Opt. Lett. 2016. V. 41. No 22. P. 5194.

  10. Carlsson A.H., Malmberg J.N., Anderson D. et al. // Opt. Lett. 2000. V. 25. No 9. P. 660.

  11. Malomed B.A. // Phys. D. 2019. V. 399. P. 108.

  12. Fedorov S.V., Veretenov N.A., Rosanov N.N. // Phys. Rev. Lett. 2019. V. 122. Art. No 023903.

  13. Mayteevarunyoo T., Malomed B.A., Skryabin D.V. // New J. Phys. 2018. V. 20. Art. No 113019.

  14. Sazonov S.V., Mamaikin M.S., Komissarova M.V. et al. // Phys. Rev. E. 2017. V. 96. Art. No 022208.

  15. Kalinovich A.A., Komissarova M.V., Sazonov S.V. et al. // PLoS ONE. 2019. V. 14. No 8. Art. No e0220840.

  16. Sazonov S.V., Kalinovich A.A., Komissarova M.V. et al. // Phys. Rev. A. 2019. V. 100. No 3. Art. No 033835.

  17. Kalinovich A.A., Komissarova M.V., Zakharova I.G. et al. // Proc. SPIE. 2019. V. 11026. Art. No 110260M.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал