1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 1, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 22-27

Об устойчивости интенсивных импульсов, распространяющихся в фотонно-кристаллическом оптическом волокне

В. А. Халяпин 1, 2, *, А. Н. Бугай 3

1 Федеральное государственное автономное образовательное учреждение высшего образования “Балтийский федеральный университет имени Иммануила Канта”
Калининград, Россия

2 Федеральное государственное бюджетное образовательное учреждение высшего образования “Калининградский государственный технический университет”
Калининград, Россия

3 Международная межправительственная организация Объединенный институт ядерных исследований
Дубна, Россия

* E-mail: slavasxi@gmail.com

Поступила в редакцию 20.07.2020
После доработки 28.08.2020
Принята к публикации 28.09.2020

Полный текст (PDF)

Аннотация

Аналитически исследована устойчивость солитоноподобных импульсов, распространяющихся в волокне в режиме туннельной ионизации и вынужденного комбинационного саморассеяния. Показано, что при определенных условиях на параметры среды и сигнала возможна взаимная компенсация этих эффектов.

ВВЕДЕНИЕ

Полые волноводы, заполненные газом, получили широкое распространения в связи с малыми потерями импульсов при их распространении и тем, что высокий порог оптического пробоя позволяет распространяться мощным сверхкоротким лазерным импульсам [1–3]. По мере распространения мощные импульсы вызывают ионизацию газа, которая приводит к тому, что спектр импульса смещается в сторону высоких частот, а его длительность уменьшается [4]. Это вызвано тем, что возникающие за счет ионизации свободные электроны вносят отрицательный вклад в показатель преломления [4–12]. Этот эффект противоположен вынужденному комбинационному саморассеянию (ВКС), которое вызывает красное смещение спектра сигнала и увеличение его длительности [13–19]. Известно, что компенсировать уширение импульса и красное смещение, обусловленное ВКС можно, изменяя коэффициент групповой дисперсии вдоль волновода [20‒24] и за счет градиента давления газа [25–27], который приводит к изменению коэффициента нелинейности. Уравнение, описывающее распространение импульсов с учетом ВКС и туннельной ионизации было получено в работах [8, 9]. С помощью теории возмущений [25–27] авторы показали, что при определенных условиях центральная частота солитона может оставаться такой же, какой была на входе в волокно, а импульс может стабилизироваться [28–33]. Целью настоящей работы является исследование с помощью метода Ляпунова устойчивости стационарного решения системы уравнений на параметры сигнала. Следует отметить, что исследование на устойчивость проводилось для приближенного решения системы уравнений, полученной методом моментов. Поскольку данный метод связан с выбором пробной функции, нами проведен и анализ чувствительности метода к выбору пробной функции.

МЕТОД МОМЕНТОВ И СТАЦИОНАРНЫЕ ТОЧКИ

Динамика световых импульсов, распространяющихся в ФКВ, описывается уравнением [8, 9]

(1)
$\begin{gathered} \frac{{\partial \psi }}{{\partial z}} + \frac{{i{{\beta }_{2}}}}{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{\tau }^{2}}}} - \frac{{{{\beta }_{3}}}}{6}\frac{{{{\partial }^{3}}\psi }}{{\partial {{\tau }^{3}}}} - i\gamma \psi {{\left| \psi \right|}^{2}} + \\ + \,\,\frac{\gamma }{\omega }\frac{\partial }{{\partial \tau }}\left( {\psi {{{\left| \psi \right|}}^{2}}} \right) + i\gamma {{T}_{R}}\psi \frac{{\partial {{{\left| \psi \right|}}^{2}}}}{{\partial \tau }} + i\eta \psi \int\limits_{ - \infty }^{\tau } {\delta \Theta \left( \delta \right)d\tau } = 0. \\ \end{gathered} $

Здесь ψ – медленно меняющаяся огибающая, z – ось, вдоль которой распространяется сигнал, τ = = t ‒ z/υg – время в сопутствующей системе координат, υg – групповая скорость импульса на его центральной частоте ω, η – коэффициент, характеризующий туннельную ионизацию, $\delta = {{\left| \psi \right|}^{2}} - \left| \psi \right|_{{th}}^{2},$ Θ – функция Хевисайда, $\left| \psi \right|_{{t\square }}^{2}$ – величина, пропорциональная пороговой интенсивности туннельной ионизации, ${{\beta }_{2}}$ – коэффициент дисперсии групповой скорости (ДГС), ${{\beta }_{3}}$ – положительный параметр, определяющий дисперсию третьего порядка, γ – коэффициент кубической нелинейности, ${{T}_{R}}$ – характеризует вклад ВКС. Коэффициент ${{\beta }_{2}}$ положителен, если центральная частота импульса лежит в области нормальной дисперсии групповой скорости и отрицателен в противоположном случае [34]. В уравнении (1) мы пренебрегли поглощением волновода и потерями, связанными с ионизацией, поскольку вблизи порога туннельной ионизации нелинейное поглощение мало. Авторами работ [8, 9] для таких импульсов было введено название “floating soliton”.

Медленно меняющаяся огибающая связана с электрическим полем импульса E соотношением

(2)
$E(z,\tau ) = \frac{1}{2}\psi (z,\tau )\exp \left[ { - i\left( {\omega t - kz} \right)} \right] + c.c.,$
где k – волновое число. Анализ динамики параметров импульса проводился на основе метода моментов [17, 35–37]. Здесь важную роль играет выбор пробной функции. В частности, в [17] влияние ВКС на динамику импульсов было исследовано на основе пробного решения в виде гауссова профиля и гиперболического секанса. Было показано, что для обеих функций получаются качественно совпадающие результаты. В работе [31] было проведено исследование динамики импульсов при учете ВКС и ионизации в солитонном и несолитонном режимах. На основе сравнения численного эксперимента и аналитических результатов было показано, что пробное решение в виде гауссовой функции лучше описывает несолитонную динамику сигнала в области нормальной дисперсии групповых скоростей, в то время как солитонный режим лучше описывается гиперболическим секансом. Действительно, если опустить высшую нелинейность и дисперсию, а также члены, описывающие ВКС и ионизацию, то пробная функция должна описывать солитон нелинейного уравнения Шредингера. Вследствие этих соображений выбираем огибающую импульса в виде гиперболического секанса [17]
(3)
$\begin{gathered} \psi = B\operatorname{sech} \left( {\frac{{\tau - T}}{{{{\tau }_{p}}}}} \right) \times \\ \times \,\,\exp \left[ {i\left( {\phi + \Omega \left( {\tau - T} \right) - C\frac{{{{{\left( {\tau - T} \right)}}^{2}}}}{{2\tau _{p}^{2}}}} \right)} \right], \\ \end{gathered} $
где B – амплитуда сигнала, ${{\tau }_{p}}$ – его длительность, C – параметр, определяющий частотную модуляцию, T – временное запаздывание, ϕ – фаза и Ω – смещение центральной частоты сигнала. Все параметры зависят от координаты z. Определим моменты импульса, следуя работе [17] в виде
(4)
$E = \int\limits_{ - \infty }^\infty {{{{\left| \psi \right|}}^{2}}d\tau } ,$
(5)
$\tilde {C} = \frac{i}{{2E}}\int\limits_{ - \infty }^\infty {\left( {\tau - T} \right)\left( {\psi {\text{*}}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial \psi {\text{*}}}}{{\partial \tau }}} \right)d\tau } ,$
(6)
${{\sigma }^{2}} = \frac{1}{E}\int\limits_{ - \infty }^\infty {{{{\left( {\tau - T} \right)}}^{2}}{{{\left| \psi \right|}}^{2}}d\tau } ,$
(7)
$T = \frac{1}{E}\int\limits_{ - \infty }^\infty {\tau {{{\left| \psi \right|}}^{2}}d\tau } ,$
(8)
$\Omega = - \frac{i}{{2E}}\int\limits_{ - \infty }^\infty {\left( {\psi {\text{*}}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial \psi {\text{*}}}}{{\partial \tau }}} \right)d\tau } ,$
где E – параметр, пропорциональный числу фотонов, $\tau _{p}^{2} = {{12{{\sigma }^{2}}} \mathord{\left/ {\vphantom {{12{{\sigma }^{2}}} {{{\pi }^{2}}}}} \right. \kern-0em} {{{\pi }^{2}}}},$ $C = {{12\tilde {С}} \mathord{\left/ {\vphantom {{12\tilde {С}} {{{\pi }^{2}}}}} \right. \kern-0em} {{{\pi }^{2}}}}$ [17]. Дифференцируя (4)–(8) по координате z и используя (1), получаем систему уравнений, подставляя в которую пробную функцию (3) и интегрируя по τ, получаем систему уравнений на параметры импульса [38]

(9)
$E = 2{{\tau }_{p}}{{B}^{2}} = {\text{const}},$
(10)
$\frac{{d\Omega }}{{dz}} = \frac{{4\gamma E}}{{15\tau _{p}^{3}}}\left( {{{T}_{R}} - \frac{{5C}}{{4\omega }}} \right) - \frac{{\eta E}}{{3{{\tau }_{p}}}}{{\left( {1 - \frac{{\psi _{{th}}^{2}}}{{{{B}^{2}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}},$
(11)
$\frac{{d\tau _{p}^{2}}}{{dz}} = 2C\left( {{{\beta }_{2}} - {{\beta }_{3}}\Omega } \right),$
(12)
$\frac{{dС}}{{dz}} = \left( {{{\beta }_{2}} - {{\beta }_{3}}\Omega } \right)\left( {\frac{{{4 \mathord{\left/ {\vphantom {4 {{{\pi }^{2}}}}} \right. \kern-0em} {{{\pi }^{2}}}} + {{С}^{2}}}}{{\tau _{p}^{2}}}} \right) + \frac{{2\gamma E}}{{{{\pi }^{2}}{{\tau }_{p}}}}\left( {1 - \frac{\Omega }{\omega }} \right),$
(13)
$\frac{{dT}}{{dz}} = - {{\beta }_{2}}\Omega + \frac{{{{\beta }_{3}}}}{2}\left( {\frac{{\left( {1 + {{{{\pi }^{2}}{{C}^{2}}} \mathord{\left/ {\vphantom {{{{\pi }^{2}}{{C}^{2}}} 4}} \right. \kern-0em} 4}} \right)}}{{3\tau _{p}^{2}}} + {{\Omega }^{2}}} \right) + \frac{{\gamma E}}{{2\omega {{\tau }_{p}}}}.$

Уравнение для фазы не приводится, поскольку она не играет роли в дальнейшем анализе. Рассмотрим сначала случай постоянного коэффициента нелинейности, соответствующий постоянному давлению внутри полости. Из (12) следует, что в солитоноподобном режиме должно выполняться соотношение

(14)
$\Omega = \frac{{\left| {{{\beta }_{2}}} \right|}}{{{{\beta }_{3}}}}\left( {\frac{{\gamma {{\tau }_{p}}E}}{{2\left| {{{\beta }_{2}}} \right|}} - 1} \right).$

Подставляя (14) в (10), находим уравнение на длительность импульса

(15)
$\frac{{d{{\tau }_{p}}}}{{dz}} = \frac{{8{{\beta }_{3}}{{T}_{R}}}}{{15\tau _{p}^{3}}} - \frac{{2{{\beta }_{3}}\eta }}{{3\gamma {{\tau }_{p}}}}{{\left( {1 - \frac{{2{{\tau }_{p}}\psi _{{th}}^{2}}}{E}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}.$

Из (14) следует, что при начальном нулевом сдвиге частоты на входе в среду должно выполняться условие солитоноподобного распространения сигнала

(16)
$E = \frac{{2\left| {{{\beta }_{2}}} \right|}}{{\gamma {{\tau }_{0}}}},$
где τ0 – начальная длительность импульса. Введем безразмерную длительность υ = τp/τs, υ0 = = τ0/τs, b = τs/τt и перепишем (15) с учетом (16) в виде
(17)
$\frac{{d\nu }}{{dz}} = \frac{{2{{\beta }_{3}}\eta }}{{3{{\nu }^{3}}\gamma }}\left( {\frac{m}{{{{b}^{2}}}} - {{\nu }^{2}}{{{\left( {1 - \nu {{\nu }_{0}}{{b}^{2}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right),$
где m = ${{4\gamma {{T}_{R}}} \mathord{\left/ {\vphantom {{4\gamma {{T}_{R}}} {5\eta \tau _{t}^{2}}}} \right. \kern-0em} {5\eta \tau _{t}^{2}}},$ τt = $\sqrt {{{\left| {{{\beta }_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{\beta }_{2}}} \right|} {\gamma \psi _{t}^{2}}}} \right. \kern-0em} {\gamma \psi _{t}^{2}}}} .$ В стационарной точке правая часть (17) должна быть равна нулю и υ = υ0 = 1

(18)
$m = {{b}^{2}}{{\left( {1 - {{b}^{2}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}.$

Выражение (18) имеет один корень ${{b}_{1}} = \sqrt {2{\text{/}}5} ,$ если $m = {{m}_{c}}$ = $2 \cdot {{{{3}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{3}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} {{{5}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{5}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}.$ В случае, когда $m < {{m}_{c}}$ мы имеем два корня, для которых можно получить приближенные выражения, воспользовавшись методом последовательных приближений

(19)
${{b}_{2}} \approx \frac{{\sqrt m }}{{{{{\left( {1 - m} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}}},$
(20)
${{b}_{3}} \approx \sqrt {1 - {{{\left( {\frac{m}{{1 - {{m}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} .$

Если $m > {{m}_{c}},$ то (18) не имеет корней. Для того, чтобы проверить полученные стационарные решения на устойчивость обезразмерим систему (10)–(12), перейдя к новым переменным $\Theta = {\Omega \mathord{\left/ {\vphantom {\Omega \omega }} \right. \kern-0em} \omega },$ $l = {{{{\beta }_{3}}\omega } \mathord{\left/ {\vphantom {{{{\beta }_{3}}\omega } {\left| {{{\beta }_{2}}} \right|}}} \right. \kern-0em} {\left| {{{\beta }_{2}}} \right|}},$ ${{L}_{d}} = {{\tau _{s}^{2}} \mathord{\left/ {\vphantom {{\tau _{s}^{2}} {\left| {{{\beta }_{2}}} \right|}}} \right. \kern-0em} {\left| {{{\beta }_{2}}} \right|}},$ LN = 2τs/γE, LR = = ${{15\tau _{s}^{2}} \mathord{\left/ {\vphantom {{15\tau _{s}^{2}} {4\gamma E{{T}_{R}}}}} \right. \kern-0em} {4\gamma E{{T}_{R}}}},$ Lη = 3/ηE и переписав (10)–(12) в виде

(21)
$\frac{{d\Theta }}{{dz}} = \frac{1}{{\omega {{\tau }_{s}}}}\left( {\frac{1}{{{{L}_{R}}{{\upsilon }^{3}}}}\left( {1 - \frac{{5C}}{{4{{T}_{R}}\omega }}} \right) - \frac{1}{{{{L}_{{\eta }}}\upsilon }}{{{\left( {1 - \frac{{\psi _{{th}}^{2}}}{{{{B}^{2}}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right),$
(22)
$\frac{{d\nu }}{{dz}} = - \frac{C}{{{{L}_{d}}\upsilon }}(1 + l\Theta ),$
(23)
$\frac{{dC}}{{dz}} = \frac{4}{{{{\pi }^{2}}}}\left( { - \left( {1 + \frac{{{{\pi }^{2}}{{C}^{2}}}}{4}} \right)\frac{{\left( {1 + l\Theta } \right)}}{{{{L}_{d}}{{\upsilon }^{2}}}} + \frac{1}{{{{L}_{N}}\upsilon }}\left( {1 - \Theta } \right)} \right),$

Для проверки системы на устойчивость по отношению к малым отклонениям параметров импульса от стационарной точки (где выполняются условия ${{d\Theta } \mathord{\left/ {\vphantom {{d\Theta } {dz}}} \right. \kern-0em} {dz}} = 0,$ ${{d\upsilon } \mathord{\left/ {\vphantom {{d\upsilon } {dz}}} \right. \kern-0em} {dz}} = 0,$ ${{dC} \mathord{\left/ {\vphantom {{dC} {dz}}} \right. \kern-0em} {dz}} = 0,$ $\Theta (0) = 0,$ $C(0) = 0,$ $\upsilon (0) = 1$) линеаризуем (21)–(23), подставив υ = υs + $\tilde {\upsilon },$ C = Cs + $\tilde {C},$ Θ = Θs + $\Theta .$ Тогда из (21)–(23) получим

(24)
$\frac{{d\tilde {\Theta }}}{{d\xi }} = \frac{{{{L}_{d}}\sqrt {1 - {{b}^{2}}} }}{{{{L}_{{\eta }}}\omega {{\tau }_{s}}}}\left( {\frac{{\left( {7{{b}^{2}} - 4} \right)}}{2}\tilde {\nu } - \frac{{5\left( {1 - {{b}^{2}}} \right)\tilde {C}}}{{4{{T}_{R}}\omega }}} \right),$
(25)
$\frac{{d\tilde {\nu }}}{{d\xi }} = - \tilde {C},$
(26)
$\frac{{d\tilde {C}}}{{d\xi }} = \frac{4}{{{{\pi }^{2}}}}\left( {\tilde {\nu } - \left( {1 + l} \right)\tilde {\Theta }} \right),$
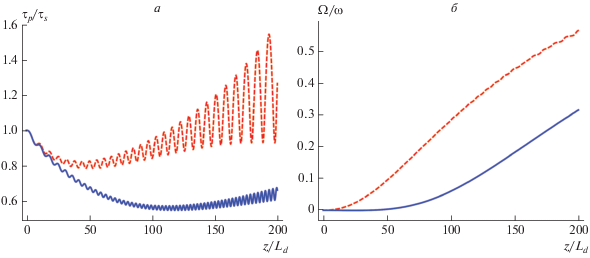
где ξ = z/Ld. Полагая в (24)–(26) $\tilde {\Theta },$ $\tilde {C},$ $\tilde {\upsilon }$ ~ exp(λξ) и находя приближенные решения характеристического уравнения, получим

(27)
$\begin{gathered} {{\lambda }_{0}} = \frac{{{{L}_{d}}(1 + l)}}{{2\omega {{\tau }_{s}}{{L}_{{\eta }}}}}\sqrt {1 - {{b}^{2}}} (7{{b}^{2}} - 4), \\ {{\lambda }_{ \pm }} = - \frac{{{{L}_{d}}(1 + l)}}{{4\omega {{\tau }_{s}}{{L}_{{\eta }}}}}\sqrt {1 - {{b}^{2}}} (7{{b}^{2}} - 4) \pm \frac{{2i}}{\pi }. \\ \end{gathered} $

Из выражений (19), (20) следует, что обе стационарные точки неустойчивы по Ляпунову. При этом, как видно из (27) в случае стационарного решения, определяемого ${{b}_{2}},$ инкремент нарастания возмущений в два раза меньше, чем для стационарного решения, определяемого ${{b}_{3}}.$ Непосредственное численное решение уравнений для параметров импульса подтверждает данный вывод (рис. 1). При этом использованы следующие безразмерные параметры: $\omega {{\tau }_{s}} = 50,$ ${{{{L}_{d}}} \mathord{\left/ {\vphantom {{{{L}_{d}}} {{{L}_{{\eta }}}}}} \right. \kern-0em} {{{L}_{{\eta }}}}} = 0.1,$ $l = 1,$ $m = 0.1.$ Для параметров в (19) и (20), получим, ${{b}_{2}} = 0.35$ и ${{b}_{3}} = 0.86,$ соответственно. В первом случае режим происходит более медленный рост длительности, чирпа и сдвига частоты. Во втором случае более заметный сдвиг частоты сопровождается стабилизацией длительности и чирпа. Поскольку характерная длина нарастания возмущений обратно пропорциональна числу колебаний импульса и на несколько порядков превосходит характерную длину дисперсионного расплывания, то указанные режимы распространения на практике вполне можно считать квазистационарными и доступными для экспериментального наблюдения.

Рис. 1.

Динамика длительности (а) и сдвига частоты (б) импульсов, при отклонении их начальных параметров от стационарных значений, определяемых величинами ${{b}_{2}}$ (красный пунктир) и ${{b}_{3}}$ (синий сплошной).

Для контроля чувствительности используемого подхода к виду пробной функции нами было проведено такое же исследование и для пробной функции гауссова профиля. Здесь получены следующие результаты

(28)
$\begin{gathered} {{\lambda }_{0}} = \frac{{6{{L}_{d}}(1 + l)}}{{\pi b\omega {{\tau }_{s}}{{L}_{{\eta }}}}}\sqrt {1 - {{b}^{2}}} (2{{b}^{2}} - 1), \\ {{\lambda }_{ \pm }} = - \frac{{3{{L}_{d}}(1 + l)}}{{\pi b\omega {{\tau }_{s}}{{L}_{{\eta }}}}}\sqrt {1 - {{b}^{2}}} (2{{b}^{2}} - 1) \pm i. \\ \end{gathered} $

Из (28) мы видим, что скорость нарастания инкремента возмущения для стационарной точки, лежащей левее $\sqrt {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} $ (в (27) это значение определяется $\sqrt {{4 \mathord{\left/ {\vphantom {4 7}} \right. \kern-0em} 7}} $) также в 2 раза меньше, чем для области лежащей правее этой точки. Отсюда можно сделать вывод, что анализ устойчивости дает качественно те же результаты, что и ранее, а метод хорошо работает и в этом случае.

Рассмотрим теперь случай, когда изменяется один из параметров волновода, например, путем создания градиента давления [27]. Пусть коэффициент, характеризующий нелинейность, меняется по закону

(29)
$\gamma = {{\gamma }_{0}}(1 + \alpha \xi ),$
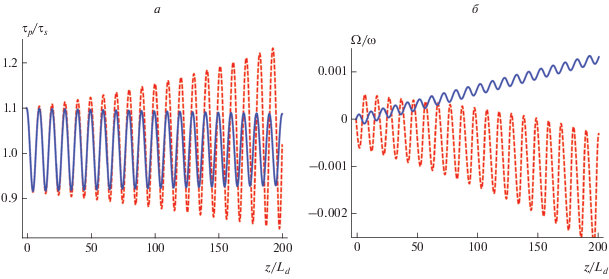
где α – положительный параметр. Исследование влияния неоднородности волновода типа (29) на устойчивость квазистационарных режимов распространения проводилось с помощью численного моделирования (рис. 2). Использовались те же параметры, что и при построении рис. 1, а также принято $\alpha = 0.01.$ Как видно из рис. 2, в случае стационарного решения, определяемого ${{b}_{2}},$ начальная компрессия импульса постепенно сменяется его расплыванием, а для стационарного решения, определяемого ${{b}_{3}},$ происходит компрессия. Подобный эффект наблюдался в волноводах с градиентом давления [27]. Однако в настоящей задаче оба режима распространения характеризуются большим смещением центральной частоты импульса в красную область спектра.

Рис. 2.

Динамика длительности (а) и сдвига частоты (б) импульсов, распространяющихся в режимах, определяемых величинами ${{b}_{2}}$ (красный пунктир) и ${{b}_{3}}$ (синий сплошной) при наличии в среде модуляции керровской нелинейности ($\alpha = 0.01$).

ЗАКЛЮЧЕНИЕ

В работе рассмотрены возможные режимы квазистационарного распространения светового импульса в режиме ВКС и туннельной ионизации, а также проведен анализ влияния градиента коэффициента нелинейности вдоль оси волновода. На основе метода моментов проведено аналитическое исследование динамики интенсивных солитоноподобных импульсов, вызывающих ионизацию. Получены аналитические выражения для длительности исходного сигнала, при которой происходит баланс ВКС и ионизации. С помощью метода Ляпунова показано, что стационарные точки не являются устойчивыми в строгом смысле и система будет медленно выходить из равновесия. В случае изменения коэффициента нелинейности вдоль оси волновода выявлена динамика сигнала, сопровождающаяся компрессией или расплыванием импульса, центральная частота которого непрерывно смещается в красную область спектра.

Работа выполнена при финансовой поддержке РФФИ (проект № 19-02-00234а).

Список литературы

  1. Couny F., Benabid F., Light P.S. // Opt. Lett. 2006. V. 31. P. 3574.

  2. Couny F., Roberts P.J., Birks T.A. et al. // Opt. Expr. 2008. V. 16. Art. No 20626.

  3. Couny F., Benabid F., Roberts P.J. et al. // Science. 2007. V. 318. P. 1118.

  4. Serebryannikov E.E., Zheltikov A.M. // Phys. Rev. A. 2007. V. 76. Art. No 013820.

  5. Wood W.M., Siders C.W., Downer M.C. // Phys. Rev. Lett. 1991. V. 67. P. 3523.

  6. Wilks S.C., Dawson J.M., Mori W.B. // Phys. Rev. Lett. 1988. V. 61. P. 337.

  7. Yablonovitch E. // Phys. Rev. A. 1974. V. 10. Art. No 1888.

  8. Hölzer P., Chang W., Travers J.C. et al. // Phys. Rev. Lett. 2011. V. 107. Art. No 203902.

  9. Hölzer P., Chang W., Travers J.C. et al. // Phys. Rev. Lett. 2011. V. 107. Art. No 203901.

  10. Saleh M.F., Biancalana F. // Phys. Rev. A. 2011. V. 84. Art. No 063838.

  11. Facão M., Carvalho M.I., Almeida P. // Phys. Rev. A. 2013. V. 87. Art. No 063803.

  12. Facão M., Carvalho M.I. // Appl. Phys. B. 2014. V. 116. P. 353.

  13. Дианов Е.М., Карасик А.Я., Мамышев П.В. и др. // Письма в ЖЭТФ. 1985. Т. 41. № 6. С. 242; Dianov E.M., Karasik A.Ya., Mamyshev P.V. et al. // JETP Lett. 1985. V. 41. No 6. P. 294.

  14. Mitschke F.M., Mollenauer L.F. // Opt. Lett. 1986. V. 11. P. 659.

  15. Gordon J.P. // Opt. Lett. 1986. V. 11. P. 662.

  16. Agrawal G.P. Nonlinear fiber optics. N.Y.: Academic, 2007.

  17. Santhanam J., Agraval G. // Opt. Commun. 2003. V. 222. P. 413.

  18. Bugay A.N., Khalyapin V.A. // Phys. Lett. A. 2017. V. 381. No 4. P. 399.

  19. Бугай А.Н., Халяпин В.А. // Опт. и спектроск. 2017. Т. 123. № 2. С. 171; Bugay A.N., Khalyapin V.A. // Opt. Spectrosс. 2017. V. 123. No 2. P. 181.

  20. Chernikov S.V., Mamyshev P.V. // JOSA B. 1991. V. 8. No 8. P. 1633.

  21. Murata H., Inagaki N. // IEEE J. Quant. Electron. 1981. V. 17. P. 835.

  22. Bogatyrjov V.A., Bubnov M.M., Dianov E.M. et al. // Pure Appl. Opt. 1995. V. 4. P. 345.

  23. Tajima K. // Opt. Lett. 1987. V. 12. P. 54.

  24. Gérôme F., Cook K., George A.K. et al. // Opt. Expr. 2007. V. 15. No 12. Art. No 7126.

  25. Nurhuda M., Suda A., Midorikawa K. et al. // JOSA B. 2003. V. 20. No 9. P. 2002.

  26. Suda A., Hatayama M., Nagasaka K. et al. // Appl. Phys. Lett. 2005. V. 86. Art. No 111116.

  27. Laegsgaard A., Roberts P.J. // Opt. Lett. 2009. V. 34. No 23. P. 3710.

  28. Serkin V.N., Vysloukh V.A. Nonlinear guided wave phenomena. Tech. digest. V. 15. OSA., 1993. P. 236.

  29. Serkin V.N., Vysloukh V.A., Taylor J.R. // Electron. Lett. 1993. V. 29. P. 12.

  30. Серкин В.Н., Беляева Т.Л., Корро Г.Х. и др. // Квант. электрон. 2003. Т. 33. С. 325; Serkin V.N., Belyaeva T.L., Corro G.H. et al. // Quant. Electron. 2003. V. 33. P. 456.

  31. Bugay A.N., Khalyapin V.A. // Commun. Nonlin. Sci. 2019. V. 75. P. 270.

  32. Bugay A.N., Khalyapin V.A. // Laser Phys. 2019. V. 29. Art. No 035402.

  33. Халяпин В.А. // Изв. РАН. Cер. физ. 2019. Т. 83. № 1. С. 32; Khalyapin V.A. // Bull. Russ. Acad. Sci. Phys. 2019. V. 83. No 1. P. 24.

  34. Козлов С.А., Сазонов С.В. // ЖЭТФ. 1997. Т. 111. С. 404; Kozlov S.A., Sazonov S.V. // JETP. 1997. V. 84. P. 221.

  35. Tsoy E.N., de Sterke C.M. // JOSA B. 2006. V. 23. P. 2425.

  36. Tsoy E.N., de Sterke C. M. // Phys. Rev. A. 2007. V. 76. Art. No 043804.

  37. Маймистов А.И. // ЖЭТФ. 1993. Т. 104. С. 3620, Maimistov A.I. // JETP. 1993. V. 77. P. 727.

  38. Халяпин В.А. // Изв. РАН. Cер. физ. 2020. Т. 84. № 1. С. 16; Khalyapin V.A. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No 1. P. 10.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал