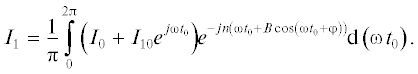Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 98-105

О теории гибрида лампы бегущей волны с фотокатодом и усилителя с комплексной диэлектрической проницаемостью

А. А. Фунтов^*

Федеральное государственное бюджетное образовательное учреждение высшего образования “Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского”
Саратов, Россия

^* E-mail: aafuntov@mail.ru

Поступила в редакцию 20.07.2020
После доработки 28.08.2020
Принята к публикации 28.09.2020

DOI: 10.31857/S0367676521010117

Полный текст (PDF)

Аннотация

Изложена теория гибрида лампы бегущей волны (ЛБВ) с фотокатодом и усилителя с комплексной диэлектрической проницаемостью. В секции с комплексной диэлектрической проницаемостью в первом случае используется линейная теория усилителя c комплексной диэлектрической проницаемостью, а в ЛБВ-секции – линейная теория ЛБВ. Для построения нелинейной теории используется метод заданного движения и метод заданного тока.

ВВЕДЕНИЕ

В связи с активным развитием радиофотоники, одним из направлений которой является работа с СВЧ-сигналами с помощью оптических методов, представляется важным вновь вернуться к лампе бегущей волны (ЛБВ) с фотокатодом (фото-ЛБВ) в видоизмененном варианте, рассмотрев гибрид фото-ЛБВ с усилителем с комплексной диэлектрической проницаемостью (в дальнейшем КДП).

Следует отметить, что случай отрицательной действительной компоненты КДП фактически один из видов СВЧ-метаматериалов. Вакуумные электронные приборы с такими метаматериалами могут иметь малые размеры, высокую мощность, высокий КПД и большой коэффициент усиления [1]. Такие приборы имеют многообещающие приложения в радиолокации, системах связи, ускорителях и многих других областях. Также следует отметить высокий интерес исследователей к метаматериалам, выраженный статьях и докладах на соответствующих конференциях (см., например, [1–4]). Отдельно упомянем работу [6], посвященную метаматериалам в ТГц-диапазоне.

Предлагаемая гибридизация должна позволить сохранить все присущие фото-ЛБВ особенности с возможным улучшением характеристик за счет вставки между фотокатодом и отрезком спирали секции с КДП (см. рис. 1). За счет использования КДП-усиления это позволит сократить длину прибора. При этом гибрид остается широкополосным.

Рис. 1.

Рассматриваемая модель. $\tilde {I}\left( 0 \right),$ $\tilde {\upsilon }\left( 0 \right)$ – начальные возмущения тока и скорости на входе в секцию с комплексной диэлектрической проницаемостью, $\tilde {I}{{\left( 0 \right)}_{p}},$ $\tilde {\upsilon }{{\left( 0 \right)}_{p}}$ – начальные возмущения тока и скорости на входе в ЛБВ-секцию.

Далее используем нелинейные уравнения для волн пространственного заряда в среде с комплексной проводимостью [7]. При прохождении бесконечно широкого (по осям у и z) потока через такую среду плотность тока можно представить в виде

(1)

$i = - \sigma E - \frac{{e{{\rho }_{0}}}}{{m\omega _{p}^{2}}}\frac{{\partial E}}{{\partial t}} - \frac{1}{{{{B}_{L}}}}\int {E{\text{d}}t} ,$

где σ – активная компонента проводимости, ${{B}_{L}}$ – коэффициент индуктивности, $e{\text{/}}m$ – удельный заряд электрона, ${{\rho }_{0}}$ – средняя плотность заряда в потоке, $~{{\varepsilon }_{0}}$ – диэлектрическая проницаемость вакуума, ${{\omega }_{p}}$ = $\sqrt {\frac{{e{{\rho }_{0}}}}{{m{{\varepsilon }_{0}}}}} $ – плазменная частота, E – продольная компонента напряженности электрического поля. Уравнение движения в этом случае примет вид

(2)

$\frac{{\partial \upsilon }}{{\partial t}} + \upsilon \frac{{\partial \upsilon }}{{\partial x}} = \frac{e}{m}E.$

Продифференцировав (2) по t и использовав (1) получим

(3)

$\begin{gathered} \frac{{{{\partial }^{2}}\upsilon }}{{\partial {{t}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial t\partial x}}\left( {\frac{{{{\upsilon }^{2}}}}{2}} \right) + \frac{\sigma }{{{{\varepsilon }_{0}}}}\left( {\frac{{\partial \upsilon }}{{\partial t}} + \upsilon \frac{{\partial \upsilon }}{{\partial x}}} \right) + \\ + \,\,\frac{1}{{{{\varepsilon }_{0}}{{B}_{L}}}}\int {\left( {\frac{{\partial \upsilon }}{{\partial t}} + \upsilon \frac{{\partial {v}}}{{\partial x}}} \right){\text{d}}t} = - \omega _{p}^{2}{{\upsilon }_{0}}\frac{I}{{{{I}_{0}}}}, \\ \end{gathered} $

где υ₀ – средняя скорость пучка, υ – скорость пучка, I – ток пучка, ${{I}_{0}}$ – средний ток пучка. Из уравнения непрерывности нетрудно получить

(4)

${{\upsilon }^{2}}\frac{{\partial I}}{{\partial x}} + \upsilon \frac{{\partial I}}{{\partial t}} - I\frac{{\partial \upsilon }}{{\partial t}} = 0.$

Линеаризуем уравнения (3) и (4). Предположим, что $I = {{I}_{0}} + \tilde {I}$ и $\upsilon = {{\upsilon }_{0}} + \tilde {\upsilon },$ причем $\tilde {I} \ll {{I}_{0}},$ $\tilde {\upsilon } \ll {{\upsilon }_{0}}.$ Тогда уравнения (3) и (4) можно представить в виде

(5)

$\begin{gathered} \frac{{{{\partial }^{2}}\tilde {\upsilon }}}{{\partial {{t}^{2}}}} + {{\upsilon }_{0}}\frac{{{{\partial }^{2}}\tilde {\upsilon }}}{{\partial t\partial x}} + \frac{\sigma }{{{{\varepsilon }_{0}}}}\left( {\frac{{\partial{ \tilde {\upsilon }}}}{{\partial t}} + {{\upsilon }_{0}}\frac{{\partial{ \tilde {\upsilon }}}}{{\partial x}}} \right) + \frac{1}{{{{\varepsilon }_{0}}{{B}_{L}}}} \times \\ \times \,\,\int {\left( {\frac{{\partial{ \tilde {\upsilon }}}}{{\partial t}} + {{\upsilon }_{0}}\frac{{\partial{ \tilde {\upsilon }}}}{{\partial x}}} \right){\text{d}}t} = - \omega _{p}^{2}{{\upsilon }_{0}}\frac{{\tilde {I}}}{{{{I}_{0}}}}, \\ \end{gathered} $

(6)

$\upsilon _{0}^{2}\frac{{\partial{ \tilde {I}}}}{{\partial x}} + {{\upsilon }_{0}}\frac{{\partial{ \tilde {I}}}}{{\partial t}} - {{I}_{0}}\frac{{\partial{ \tilde {\upsilon }}}}{{\partial t}} = 0.$

Предполагая, что все переменные величины $\sim {\kern 1pt} {{e}^{{j{\omega }t}}}$ (где $j = \sqrt { - 1} ,$ ω – рабочая частота), получим

(7)

$\left( {j\omega {{\upsilon }_{0}}\frac{{\partial {\tilde {v}}}}{{\partial x}} - {{\omega }^{2}}\tilde {\upsilon }} \right)\left( {1 - j\frac{{\sigma + jL}}{{\omega {{\varepsilon }_{0}}}}} \right) = - \omega _{p}^{2}{{\upsilon }_{0}}\frac{{\tilde {I}}}{{{{I}_{0}}}},$

(8)

$\upsilon _{0}^{2}\frac{{\partial{ \tilde {I}}}}{{\partial x}} + j\omega \left( {{{\upsilon }_{0}}\tilde {I} - {{I}_{0}}\tilde {\upsilon }} \right) = 0,$

где $L = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} {\left( {\omega {{B}_{L}}} \right)}}} \right. \kern-0em} {\left( {\omega {{B}_{L}}} \right)}}.$ Из (7) и (8) нетрудно получить (опуская в дальнейшем тильды)

(9)

$\frac{{{{\partial }^{2}}I}}{{\partial {{x}^{2}}}} + 2j{{\beta }_{e}}\frac{{\partial I}}{{\partial x}} - \left( {\beta _{e}^{2} - \frac{{\beta _{p}^{2}}}{{1 + \frac{{L - j\sigma }}{{\omega {{\varepsilon }_{0}}}}}}} \right)I = 0,$

где ${{\beta }_{p}} = {{{{\omega }_{p}}} \mathord{\left/ {\vphantom {{{{\omega }_{p}}} {{{\upsilon }_{0}}}}} \right. \kern-0em} {{{\upsilon }_{0}}}},$ ${{\beta }_{e}} = {\omega \mathord{\left/ {\vphantom {\omega {{{\upsilon }_{0}}}}} \right. \kern-0em} {{{\upsilon }_{0}}}}.$

Рассмотрим следующую модель: на катод падает амплитудно-модулированный световой сигнал и поэтому можно считать, что максимальная величина переменной составляющей фототока $I = m{{I}_{0}},$ где m – параметр, характеризующий глубину модуляции, ${{I}_{0}}$ – средний фототок. Ограничимся в дальнейшем линейной теорией, предполагая, что $m \ll 1.$ Считаем, что на входе в секцию с комплексной диэлектрической проницаемостью пучок имеет модуляцию по скорости и току.

Отметим, что среда с КДП – фактически один из вариантов резистивного усилителя. В дальнейшем будем называть ее первой секцией. В линейной теории КДП-усилителя, а значит и в первой секции исследуемого гибрида, выражения для переменной скорости и тока, как следует из (7)–(9), примут вид

(10)

$\frac{I}{{{{I}_{0}}}} = {{e}^{{ - j{{{\beta }}_{e}}{{x}_{1}}}}}\left[ {\frac{{I\left( 0 \right)}}{{{{I}_{0}}}}\cos \frac{{{{\beta }_{p}}{{x}_{1}}}}{{\sqrt \varepsilon }} + j\frac{{\upsilon \left( 0 \right)}}{{{{\upsilon }_{0}}}}\frac{{\omega \sqrt \varepsilon }}{{{{\omega }_{p}}}}\sin \frac{{{{\beta }_{p}}{{x}_{1}}}}{{\sqrt \varepsilon }}} \right],$

(11)

$\frac{\upsilon }{{{{\upsilon }_{0}}}} = {{e}^{{ - j{{{\beta }}_{e}}{{x}_{1}}}}}\left[ {\frac{{\upsilon \left( 0 \right)}}{{{{\upsilon }_{0}}}}\cos \frac{{{{\beta }_{p}}{{x}_{1}}}}{{\sqrt \varepsilon }} + j\frac{{I\left( 0 \right)}}{{{{I}_{0}}}}\frac{{\omega \sqrt \varepsilon }}{{{{\omega }_{p}}}}\sin \frac{{{{\beta }_{p}}{{x}_{1}}}}{{\sqrt \varepsilon }}} \right],$

где ${{x}_{1}}$ – длина первой (КДП) секции, ε – относительная комплексная диэлектрическая проницаемость среды. Средний заряд электронов скомпенсирован ионным фоном.

Считаем далее $\varepsilon = 1$ + $\frac{{L - j\sigma }}{{\omega {{\varepsilon }_{0}}}}.$ Введем для удобства, $L{\kern 1pt} ' = \frac{L}{{\omega {{\varepsilon }_{0}}}}$ и $\sigma {\kern 1pt} ' = \frac{\sigma }{{\omega {{\varepsilon }_{0}}}},$ тогда $\varepsilon = 1$ + $L{\kern 1pt} '\,\, - j\sigma {\kern 1pt} '$ (штрихи в дальнейшем опустим).

Во второй секции, служащей для усиления и вывода сигнала, воспользуемся известной теорией фото-ЛБВ [8]. Будем использовать следующее уравнение возбуждения линии передачи

(12)

$E\left( x \right) = - \frac{{\beta _{0}^{2}K}}{2}\int\limits_0^x {I\left( \zeta \right){{e}^{{ - j\left( {{{{\beta }}_{0}} - j{{{\gamma }}_{0}}} \right)\left( {x - {\zeta }} \right)}}}d\zeta } ,$

где x – координата во второй секции, ${{\beta }_{0}}$ – постоянная распространения в линии без пучка, ${{\gamma }_{0}}$ – затухание в линии передачи на единицу длины, K – сопротивление связи. В качестве начальных условий для второй секции $I{{\left( 0 \right)}_{p}},$ $\upsilon {{\left( 0 \right)}_{p}}$ будем использовать значения из уравнений (10) и (11) на выходе первой секции.

Как известно (см., например, [8]), основная характеристика фотоприборов – эквивалентное сопротивление

(13)

${{R}_{{{\text{экв}}}}} = \frac{{{{{\left| E \right|}}^{2}}}}{{\beta _{0}^{2}K{{{\left| {I\left( 0 \right)} \right|}}^{2}}}}.$

Для удобства введем ${{C}^{3}} = \frac{{{{I}_{0}}K}}{{4{{V}_{0}}}},$ $q = {{\left( {\frac{{{{\omega }_{p}}}}{\omega }} \right)}^{2}},$ $~E{\kern 1pt} ' = \frac{E}{{{{V}_{0}}{{\beta }_{e}}}},$ $I{\kern 1pt} '\left( 0 \right) = \frac{{I\left( 0 \right)}}{{{{I}_{0}}}},$ $\upsilon {\kern 1pt} '\left( 0 \right) = \frac{{\upsilon \left( 0 \right)}}{{{{{v}}_{0}}}},$ $\xi = {{\beta }_{e}}x,$ $\beta _{0}^{'} - j\gamma _{0}^{'}$ = $\frac{{{{\beta }_{0}} - j{{\gamma }_{0}}}}{{{{\beta }_{e}}}}$ (штрихи в дальнейшем опустим). При малом параметре усиления $C \ll 1$ во второй секции (в нормировке настоящей работы) [9]

(14)

$\begin{gathered} E = - 2j{{C}^{2}}I{{\left( 0 \right)}_{p}}\left[ {\frac{{\left( {{{\delta }_{2}}{{\delta }_{3}} - \frac{q}{{{{C}^{2}}}}} \right)\left( {\delta _{1}^{2} + \frac{q}{{{{C}^{2}}}}} \right)}}{{\left( {{{\delta }_{1}} - {{\delta }_{2}}} \right)\left( {{{\delta }_{1}} - {{\delta }_{3}}} \right)}}{{e}^{{{{{\delta }}_{1}}{\xi }}}} + } \right. \\ + \,\,\frac{{\left( {{{\delta }_{1}}{{\delta }_{3}} - \frac{q}{{{{C}^{2}}}}} \right)\left( {\delta _{2}^{2} + \frac{q}{{{{C}^{2}}}}} \right)}}{{\left( {{{\delta }_{2}} - {{\delta }_{3}}} \right)\left( {{{\delta }_{2}} - {{\delta }_{1}}} \right)}}{{e}^{{{{{\delta }}_{{\text{2}}}}{\xi }}}} + \\ \left. { + \,\,\frac{{\left( {{{\delta }_{1}}{{\delta }_{2}} - \frac{q}{{{{C}^{2}}}}} \right)\left( {\delta _{3}^{2} + \frac{q}{{{{C}^{2}}}}} \right)}}{{\left( {{{\delta }_{3}} - {{\delta }_{1}}} \right)\left( {{{\delta }_{3}} - {{\delta }_{2}}} \right)}}{{e}^{{{{{\delta }}_{{\text{3}}}}{\xi }}}}} \right] - 2C\upsilon {{\left( 0 \right)}_{p}} \times \\ \times \,\,\left[ {\frac{{\left( {{{\delta }_{2}} + {{\delta }_{3}}} \right)\left( {\delta _{1}^{2} + \frac{q}{{{{C}^{2}}}}} \right)}}{{\left( {{{\delta }_{1}} - {{\delta }_{2}}} \right)\left( {{{\delta }_{1}} - {{\delta }_{3}}} \right)}}{{e}^{{{{{\delta }}_{{\text{1}}}}{\xi }}}} + \frac{{\left( {{{\delta }_{1}} + {{\delta }_{3}}} \right)\left( {\delta _{2}^{2} + \frac{q}{{{{C}^{2}}}}} \right)}}{{\left( {{{\delta }_{2}} - {{\delta }_{3}}} \right)\left( {{{\delta }_{2}} - {{\delta }_{1}}} \right)}}{{e}^{{{{{\delta }}_{{\text{2}}}}{\xi }}}} + } \right. \\ \left. { + \,\,\frac{{\left( {{{\delta }_{1}} + {{\delta }_{2}}} \right)\left( {\delta _{3}^{2} + \frac{q}{{{{C}^{2}}}}} \right)}}{{\left( {{{\delta }_{3}} - {{\delta }_{1}}} \right)\left( {{{\delta }_{3}} - {{\delta }_{2}}} \right)}}{{e}^{{{{{\delta }}_{{\text{3}}}}{\xi }}}}} \right], \\ \end{gathered} $

где ${{\delta }_{i}}$ – нормированные корни дисперсионного уравнения

(15)

${{\delta }^{3}} + {{a}_{1}}{{\delta }^{2}} + {{a}_{2}}\delta + {{a}_{3}} = 0,$

где при $C \ll 1,$ ${{a}_{1}} = jb + d,$ ${{a}_{2}} = \frac{q}{{{{C}^{2}}}},$ ${{a}_{3}} = j$ + $ + \,\,\frac{q}{{{{C}^{2}}}}\left( {jb + d} \right),$ $b = \frac{{{{\beta }_{0}} - 1}}{C}$ = $\frac{{{{\upsilon }_{0}} - {{\upsilon }_{{\text{ф}}}}}}{{C{{\upsilon }_{{\text{ф}}}}}},$ ${{\upsilon }_{{\text{ф}}}}$ – фазовая скорость волны во второй секции без пучка, d – параметр распределенных потерь. Будем теперь полагать ${{\beta }_{0}} = 1 + Cb.$ Тогда с учетом введенных величин (13) примет вид

(16)

$\frac{{{{R}_{{{\text{экв}}}}}}}{K} = \frac{{{{{\left| E \right|}}^{2}}}}{{16{{{\left( {1 + Cb} \right)}}^{2}}{{{\left| {I\left( 0 \right)} \right|}}^{2}}{{C}^{6}}}}.$

Рассмотрим влияние параметров на ${{R}_{{{\text{экв}}}}}.$ Из рис. 2а видно, что ${{R}_{{{\text{экв}}}}}$ периодично по длине 2‑й секции (ЛБВ), это объясняется явлением QC-спада¹ ¹, а представленные на рис. 2а зависимости аналогичны функции, полученной в первом приближении в [8], которая также периодична. Из рис. 2б видно, что при $L < - 1$ и при $\sigma \to \infty $ ${{R}_{{{\text{экв}}}}}$ возрастает с увеличением длины 2-й секции, что объясняется наличием КДП-неустойчивости, а в случае когда неустойчивости нет (приведенном для сравнения) ${{R}_{{{\text{экв}}}}}$ периодично.

Рис. 2.

$\frac{{{{R}_{{{\text{экв}}}}}}}{K}$ (а) от ξ (длины ЛБВ-секции) при ${{\xi }_{1}} = 3,$ $b = 0,$ $q = 0.01,$ $C = 0.01.$ (б) от ${{\xi }_{1}}$ (длины КДП-секции) при $\xi = 3,$ $b = 0,$ $q = 0.01,$ $C = 0.01.$ Кривые на рис. (а) и (б): сплошная – $L = \sigma = 0,$ пунктир $\sigma = 0,$ $L = - 1.1,$ штрих-пунктир $\sigma = {{10}^{6}},$ $L = 0.$ (в) от b при $q = 0.01,$ $C = 0.01.$ (г) от C при $b = 0,$ $q = 0.01.$ Кривые на рис. (в) и (г): сплошная – классическая фото-ЛБВ $L = \sigma = 0,$ ${{\xi }_{1}} = 0,$ $\xi = 6;$ пунктир $L = \sigma = 0,$ ${{\xi }_{1}} = \xi = 3;$ штрих-пунктир $\sigma = 0,$ $L = - 1.1,$ ${{\xi }_{1}} = \xi = 3;$ точки $\sigma = {{10}^{6}},$ $L = 0,$ ${{\xi }_{1}} = \xi = 3;$ (д) от C при $b = 0,$ $\sigma = 0,$ $L = - 1.1$ и различных q: сплошная – $q = {{10}^{{ - 4}}},$ пунктир 10^–3, штрих-пунктир 10^–2, точки 10^–1. Все графики построены при $I\left( 0 \right)$ = $\upsilon \left( 0 \right) = {{10}^{{ - 3}}},$ $d = 0.$

Из рис. 2в видно, что ${{R}_{{{\text{экв}}}}}$ осциллирует с изменением параметра b при фиксированной длине прибора, причем при выбранных параметрах оптимальное значение ${{R}_{{{\text{экв}}}}}$ достигается при $\left| b \right| = 10,$ что объясняется эффектами пространственного заряда. Кроме того, при одинаковой полной длине эквивалентное сопротивление исследуемого гибрида (при подборе параметров) больше, чем у классической фото-ЛБВ на несколько порядков. “Колебания” ${{R}_{{{\text{экв}}}}}$ объясняется периодичной зависимостью ${{R}_{{{\text{экв}}}}}$ от ξ.

Из рис. 2г, 2д видно, что ${{R}_{{{\text{экв}}}}}$ периодично от C из-за периодичности QC-спада: при фиксированной длине QC-спад может наблюдаться при различных значениях q и C.

Из рис. 3а видно, что ${{R}_{{{\text{экв}}}}}$ сначала увеличивается с ростом σ, а затем выходит на насыщение. В теории КДП-усилителя мнимые корни дисперсионного уравнения имеют экстремум в зависимости от σ, по существу являющегося параметром потерь. Однако увеличение потерь приводит к расширению частотной области, в которой возможна КДП-неустойчивость [7]. Таким образом одновременное увеличение потерь и расширение частотной области приводят к виду полученной на рис. 3а зависимости. Из рис. 3б видно, что при прочих равных наибольшее значение ${{R}_{{{\text{экв}}}}}$ достигается при индуктивной проводимости, т.к. при чисто индуктивной проводимости ($\sigma = 0,$ $L < 0$) при выполнении условия $L = - 1$ токи смещения и индуктивные токи в среде (в первой секции) становятся равными друг другу по величине, а наведенный заряд стремится к ∞ [7]. “Колебания” ${{R}_{{{\text{экв}}}}}$ правее L = –1 объясняются численными артефактами.

Рис. 3.

$\frac{{{{R}_{{{\text{экв}}}}}}}{K}$(а) от σ при $L = 0,$ (б) от L при $\sigma = 0.$ Все графики построены при ${{\xi }_{1}} = \xi = 3,$ $I\left( 0 \right)$ = $\upsilon \left( 0 \right) = {{10}^{{ - 3}}},$ $b = 0,$ $q = 0.01,$ $C = 0.01,$ $d = 0.$

ПРИБЛИЖЕННАЯ НЕЛИНЕЙНАЯ ТЕОРИЯ ГИБРИДА ФОТО-ЛБВ И КДП-УСИЛИТЕЛЯ

Поскольку решение строгих нелинейных уравнений вызывает известные трудности, воспользуемся в первой секции описываемого гибрида методом заданного движения, развитым в работе [7], в которой проводился приближенный учет нелинейности процессов группирования в случае распространения бесконечно широкого электронного пучка в среде с индуктивной проводимостью. В настоящей работе проведено обобщение развитой в [7] теории на случай произвольной комплексной проводимости.

Вернемся к размерным величинам и возьмем следующие начальные условия: на входе в первую секцию $x = 0$ $i\left( 0 \right) = {{i}_{{10}}},$ $\upsilon \left( 0 \right) = {{\upsilon }_{{10}}}.$ Для удобства сравнения с [7] перепишем уравнений (10) и (11) в виде

(17)

$i = {{e}^{{ - j{{{\beta }}_{e}}x}}}\left[ {{{i}_{{10}}}{\text{ch}}{{\beta }_{p}}gx + j{{\upsilon }_{{10}}}\frac{{{{\beta }_{e}}{{\rho }_{0}}}}{{{{\beta }_{p}}g}}{\text{sh}}{{\beta }_{p}}gx} \right],$

(18)

$\upsilon = {{e}^{{ - j{{{\beta }}_{e}}x}}}\left[ {{{\upsilon }_{{10}}}{\text{ch}}{{\beta }_{p}}gx - j\frac{{{{\omega }_{p}}}}{\omega }g{{\upsilon }_{0}}\frac{{{{i}_{{10}}}}}{{{{i}_{0}}}}{\text{sh}}{{\beta }_{p}}gx} \right],$

где $jg = \frac{1}{{\sqrt {1 - j\sigma + L} }},$ ${{i}_{0}}$ – средняя плотность тока.

Выделим действительную и мнимую часть g. Тогда

(19)

$\frac{1}{{\sqrt {1 - j\sigma + L} }} = \frac{{{\text{exp}}\left[ {\frac{j}{2}{\text{arctg}}\frac{\sigma }{{1 + L}}} \right]}}{{\sqrt[4]{{{{{\left( {1 + L} \right)}}^{2}} + {{\sigma }^{2}}}}}},$

следовательно

(20)

$g\sqrt q = sq - jcq,$

где $cq$ = $\sqrt q \frac{{\cos \left[ {\frac{1}{2}{\text{arctg}}\frac{\sigma }{{1 + L}}} \right]}}{{\sqrt[4]{{{{{\left( {1 + L} \right)}}^{2}} + {{\sigma }^{2}}}}}},$ $sq$ = $ = \sqrt q \frac{{\sin \left[ {\frac{1}{2}{\text{arctg}}\frac{\sigma }{{1 + L}}} \right]}}{{\sqrt[4]{{{{{\left( {1 + L} \right)}}^{2}} + {{\sigma }^{2}}}}}}.$

Перейдем теперь к нелинейной теории группирования в области дрейфа с произвольной проводимостью следуя [7], но руководствуясь [8]. Полная скорость электронов на входе в дрейф находится из выражения (в нормированном виде)

(21)

${{\upsilon }_{1}} = {{\upsilon }_{0}} + \,\,{\text{Re}}\,\left[ {\left( {{{\upsilon }_{{10}}}{\text{ch}}{{\beta }_{p}}gx - j\frac{{{{\omega }_{p}}}}{\omega }g{{\upsilon }_{0}}\frac{{{{i}_{{10}}}}}{{{{i}_{0}}}}{\text{sh}}{{\beta }_{p}}gx} \right){{e}^{{j{\omega }{{t}_{0}}}}}} \right].$

Перейдем к переменным Лагранжа: ${{t}_{1}}\left( {x,{{t}_{0}}} \right)$ – это момент времени, в который электроны потока, влетевшие в пространство взаимодействии в момент ${{t}_{0}},$ окажутся в точке с координатой x

(22)

$\omega {{t}_{1}}\left( {x,{{t}_{0}}} \right) = \omega {{t}_{0}} + {{\beta }_{e}}x + \theta \left( {x,{{t}_{0}}} \right).$

Тогда полная скорость электронов определяется выражением

(23)

${{\upsilon }_{1}}\left( {x,{{t}_{1}}} \right) = \frac{{\partial x}}{{\partial t}} = {{\left( {\frac{{\partial t}}{{\partial x}}} \right)}^{{ - 1}}} = \frac{{{{\upsilon }_{0}}}}{{1 + \beta _{e}^{{ - 1}}\frac{{\partial \theta }}{{\partial x}}}} \Rightarrow \frac{{\partial \theta }}{{\partial x}} = {{\beta }_{e}}\left( {\frac{{{{\upsilon }_{0}}}}{{{{\upsilon }_{1}}}} - 1} \right).$

Считая, что второе и третье слагаемые в (21) малы, проинтегрируем (23) по координате от 0 до x, считая, что воздействие на пучок имеет периодический характер. Поэтому возмущение угла пролета электронов может быть представлено в виде

(24)

$\begin{gathered} \theta \left( {x,{{t}_{0}}} \right) = {{\theta }_{0}} + {\text{Re}}\left[ {{{\theta }_{1}}{{e}^{{j{\omega }{{t}_{0}}}}}} \right] = \\ = {{\theta }_{0}} + B\cos \left( {\omega {{t}_{0}} + \varphi } \right), \\ \end{gathered} $

где ${{\theta }_{0}} = \theta \left( {x = 0} \right),$ ${{\theta }_{1}} = B{{e}^{{j{\varphi }}}}$ (для простоты рассмотрен случай одной гармоники). Тогда в общем случае

(25)

$B = \sqrt {C{{a}^{2}} + S{{a}^{2}}} ,~\,\,\,\,\varphi = {\text{arctg}}\frac{{ - Sa}}{{Ca}},$

где

$\begin{gathered} Ca = \frac{{ - 1}}{{c{{q}^{2}} + s{{q}^{2}}}}\left\{ {\frac{1}{{\sqrt q }}\frac{{{{\upsilon }_{{10}}}}}{{{{\upsilon }_{0}}}}\left[ {cq{\text{ch}}\left( {sq\xi } \right)\sin \left( {cq\xi } \right)} \right.} \right. + \left. {\,\,sq\cos \left( {cq\xi } \right){\text{sh}}\left( {sq\xi } \right)} \right] + \\ + \,\,\frac{{{{i}_{{10}}}}}{{{{i}_{0}}}}\left[ {2cqsq\left( {\cos \left( {cq\xi } \right){\text{ch}}\left( {sq\xi } \right) - 1} \right)} \right. + \,\,\left. {\left. {\left( {c{{q}^{2}} - s{{q}^{2}}} \right)\sin \left( {cq\xi } \right){\text{sh}}\left( {sq\xi } \right)} \right]} \right\}, \\ \end{gathered} $

$\begin{gathered} Sa = \frac{{ - 1}}{{c{{q}^{2}} + s{{q}^{2}}}}\left\{ {\frac{1}{{\sqrt q }}\frac{{{{\upsilon }_{{10}}}}}{{{{\upsilon }_{0}}}}\left[ {sq{\text{ch}}\left( {sq\xi } \right)\sin \left( {cq\xi } \right)} \right.} \right. - \left. {cq\cos \left( {cq\xi } \right){\text{sh}}\left( {sq\xi } \right)} \right] + \\ + \,\,\frac{{{{i}_{{10}}}}}{{{{i}_{0}}}}\left[ { - 2cqsq\sin \left( {cq\xi } \right){\text{sh}}\left( {sq\xi } \right)} \right. + \left. {\left. {\,\left( {c{{q}^{2}} - s{{q}^{2}}} \right)\left( {\cos \left( {cq\xi } \right){\text{ch}}\left( {sq\xi } \right) - 1} \right)} \right]} \right\}. \\ \end{gathered} $

Если проводимость реактивная (т.е. $\sigma = 0$) и $L < - 1,$ то $sq = 0$ и $cq$ = $\sqrt {\frac{q}{{1 + L}}} $ = $j{{g}_{1}},$ где ${{g}_{1}}$ – действительное число, то

(26)

$\begin{gathered} B = \sqrt {{{{\left[ {\frac{{{{\upsilon }_{{10}}}}}{{{{g}_{1}}{{\upsilon }_{0}}}}{\text{sh}}\left( {{{g}_{1}}\xi } \right)} \right]}}^{2}} + {{{\left[ {\frac{{{{i}_{{10}}}}}{{{{i}_{0}}}}\left( {{\text{ch}}\left( {{{g}_{1}}\xi } \right) - 1} \right)} \right]}}^{2}}} , \\ ~\varphi = {\text{arctg}}\frac{{\frac{{{{i}_{{10}}}}}{{{{i}_{0}}}}\left( {{\text{ch}}\left( {{{g}_{1}}\xi } \right) - 1} \right)}}{{\frac{{{{\upsilon }_{{10}}}}}{{{{g}_{1}}{{\upsilon }_{0}}}}{\text{sh}}\left( {{{g}_{1}}\xi } \right)}}. \\ \end{gathered} $

С учетом начальной модуляции по току закон сохранения заряда для пучка примет вид:

(27)

$\left( {{{I}_{0}} + {{I}_{{10}}}{{e}^{{j{\omega }{{t}_{0}}}}}} \right){\text{d}}\left( {\omega {{t}_{0}}} \right) = I\left( {x,{{t}_{1}}} \right){\text{d}}\left( {\omega {{t}_{1}}} \right).$

Тогда формула тока первой гармоники, примет вид

(28)

Так как рассматриваем одномерный случай справедливо $\frac{{{{I}_{{10}}}}}{{{{I}_{0}}}} = \frac{{{{i}_{{10}}}}}{{{{i}_{0}}}},$ тогда окончательно получим

(29)

$\frac{{{{i}_{1}}}}{{{{i}_{0}}}} = 2\left( {\frac{{{{i}_{{10}}}}}{{{{i}_{0}}}}{{J}_{0}}\left( B \right) + {{J}_{1}}\left( B \right){{e}^{{j\left( {{\varphi } - \frac{{\pi }}{2}} \right)}}}} \right),$

где ${{J}_{i}}\left( B \right)$ – функция Бесселя первого рода i-го порядка. Таким образом, уравнение (29) отличается от аналогичного уравнения в [7] удвоенным первым слагаемым, что, по-видимому, является следствием опечатки в [7].

Во второй секции воспользуемся методом заданного тока (в размерном виде):

(30)

$\begin{gathered} E = - \frac{{K\beta _{e}^{2}}}{2}\int\limits_x^{x + l} {I\left( x \right){{e}^{{ - j{{{\beta }}_{e}}\left( {x + l - {\zeta }} \right)}}}{\text{d}}\zeta } = \\ = \frac{{jK{{\beta }_{e}}}}{{2\sqrt q }}{{I}_{0}}\frac{{{{i}_{1}}}}{{{{i}_{0}}}}\left( {1 - {{e}^{{ - j{\xi }}}}} \right). \\ \end{gathered} $

где l – длина второй секции. Тогда подставляя (29) и (30) в (13) получим искомое сопротивление.

Рисунки 4 построены при тех же параметрах, что и рис. 2. Из рис. 4а видно, что ${{R}_{{{\text{экв}}}}}$ также периодично по длине второй секции, но с большим периодом и что ${{R}_{{{\text{экв}}}}}$ больше чем в линейной теории. Из рис. 4б видно, что периодичность в случае $L = \sigma = 0$ при выбранных параметрах отсутствует и что в других случаях ${{R}_{{{\text{экв}}}}}$ медленнее растет с длиной первой секции. Зависимости ${{R}_{{{\text{экв}}}}}$ от b, σ и L качественно не изменились, а ${{R}_{{{\text{экв}}}}}$ больше на несколько порядков, поэтому соответствующие рисунки не приводятся.

Рис. 4.

$\frac{{{{R}_{{{\text{экв}}}}}}}{K}$(а) от ξ (длины ЛБВ-секции) при ${{\xi }_{1}} = 3,$ (б) от ${{\xi }_{1}}$ (длины КДП-секции) при $\xi = 3.$ Все графики построены при ${{i}_{{10}}}$ = ${{\upsilon }_{{10}}} = {{10}^{{ - 3}}},$ $b = 0,$ $q = 0.01,$ $C = 0.01,$ $d = 0.$ Кривые на графиках: сплошная – $L = \sigma = 0,$ пунктир $\sigma = 0,$ $L = - 1.1,$ штрих-пунктир $\sigma = {{10}^{6}},$ $L = 0,$ точки $\sigma = 10,$ $L = 0.$

ЗАКЛЮЧЕНИЕ

Исходя из результатов, полученных в рамках линейной теории, добавление в фото-ЛБВ секции с комплексной проводимостью между катодом и замедляющей системой позволяет на несколько порядков увеличить эквивалентное сопротивление при той же полной длине лампы. По результатам нелинейной теории подбором проводимости можно не только увеличить эквивалентное сопротивление, но сократить полную длину лампы, т.к. при тех же параметрах во многих случаях эквивалентное сопротивление больше чем в линейной теории.

Работа выполнена при поддержке РФФИ (проект № 18-02-00666).

Список литературы

Duan Z., Shapiro M.A., Gong Y. et al. // Proc. IVEC-2018. (Monterey, 2018).
Lu X., Hummelt J.S., Shapiro M.A. et al. // Proc. IVEC-2017. (London, 2017).
Rowe T., Behdad N., Booske J. // IEEE Trans. Plasma Sci. 2015. V. 43. No 7. P. 2123.
Rowe T., Behdad N., Booske J. // IEEE Trans. Plasma Sci. 2016. V. 44. No 10. P. 2476.
Lu X., Stephens J.C., Mastovsky I. et al. // Phys. Plasmas 2018. V. 25. Art. No 023102.
Jeannin M. et al. // Proc. IVEC-2019. (Busan, 2019).
Касаткин Л.В. // Радиотехн. и электрон. 1961. Т. 6. № 2. С. 267.
Шевчик В.Н., Трубецков Д.И. Аналитические методы расчета в электронике СВЧ. М.: Сов. радио, 1970. 584 с.
Цейтлин М.Б., Кац А.М. Лампа с бегущей волной. М.: Сов. радио, 1964. 308 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал