Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 64-67

ВВЕДЕНИЕ

Вопрос о возможности излучения в свободное пространство монополярного электромагнитного импульса (МЭМИ) рассматривается уже достаточно давно. Несмотря на вполне обоснованное (например, в [1]) утверждение о невозможности такого процесса при использовании источников электромагнитного излучения конечных размеров, в целом ряде научных публикаций последних лет были предложены различные механизмы реализации МЭМИ. Так, в [2], экспериментально показана возможность генерации МЭМИ инфракрасного диапазона за счет возбуждения фотоиндуцированных носителей заряда лазерным излучением длительностью 120 фс в тонкой пластинке GaAs при наличии на ней электрического смещения от 4 до 11 кВ/см. Один из способов получения пары монополярных импульсов предложен и теоретически обоснован в [3]. В качестве источника излучения рассмотрен локализованный в пространстве ток, временная зависимость которого имеет форму трапеции. Показано, что временной промежуток, разделяющий два монополярных импульса, определяется интервалом, на котором значение тока постоянно.

Возможность генерации МЭМИ была продемонстрирована также в ряде вычислительных экспериментов [4, 5]. Здесь источником монополярных импульсов выступало плоское короткое зеркало релятивистских электронов, которое падало наклонно на тонкую металлическую фольгу. Электроны, обладающие значительной кинетической энергией, преодолевали данное препятствие, в то время как для электромагнитного поля фольга была непрозрачной. В результате на поверхности металла образовывался локализованный в пространстве и перемещающийся с течением времени вдоль фольги ток, который и был источником МЭМИ.

Отметим, что МЭМИ, распространяющиеся в свободном пространстве, могут найти свое практическое применение в различных областях науки [6], техники [7], медицины [8] и т.д. В связи с этим актуальной представляется задача об управлении характеристиками МЭМИ: возможностью изменения направления распространения, фокусировки и пр. с сохранением его основного качества – монополярности. Этой проблеме посвящено достаточно большое количество публикаций. Например, в [9] проведено теоретическое исследование прохождения МЭМИ через диэлектрическую линзу, в [10] представлены результаты численного моделирования дифракции МЭМИ на диэлектрическом цилиндре. Отражение МЭМИ от идеально проводящей поверхности рассмотрено в [11].

Целью данной работы является исследование пространственно-временной структуры поля рассеяния монополярного импульса на идеально проводящем цилиндре. Вектор магнитного поля МЭМИ направлен параллельно оси этого цилиндра, что соответствует ТМ-поляризации импульса.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим двумерную прямоугольную область G свободного пространства (рис. 1), в которой задана декартова система координат xyz. Ось z перпендикулярна плоскости рисунка, ось x соответствует продольному направлению. Пусть вдоль оси x распространяется МЭМИ с плоским фронтом, ${{E}_{y}}$ и ${{H}_{z}}$ компоненты которого отличны от нуля. Такой набор компонент соответствует линейной TM-поляризации. Пространственный профиль импульса в начальный момент времени, как и в [10], соответствует следующему выражению:

где α₀ – амплитуда МЭМИ, x₀ – положение фронта импульса при t = 0, β – коэффициент, определяющий длительность импульса.

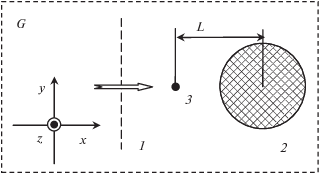
Область G содержит неоднородность: идеально проводящий цилиндр, ось которого параллельна оси z.

Найдем временную зависимость рассеянного на цилиндре поля в зависимости от его радиуса при фиксированных амплитуде и длительности МЭМИ. Заметим, что при изменении радиуса неоднородности расстояние от центра неоднородности до точки наблюдения (L, рис. 1) остается постоянным.

Для вычисления поля воспользуемся системой уравнений Максвелла в дифференциальной форме в пространственно-временном представлении, задав для компонент поля ${{E}_{x}},$ ${{E}_{y}}$ и ${{H}_{z}}$ соответствующие поставленной задаче граничные и начальные условия. Нормируем время на длительность падающего импульса τ, определяемую по уровню 0.5 амплитуды ${{E}_{y}}.$ Пространственные координаты нормируем на величину $c\tau ,$ где c – скорость света в вакууме.

Решение уравнений Максвелла будем проводить численным методом конечно-разностной аппроксимации непрерывных частных производных. Выполнение условий излучения поля на границах области обеспечим, используя метод идеально согласованного слоя [12]. Для выделения рассеянного поля из общего используем алгоритм, основанный на принципе суперпозиции электромагнитного поля, который описан в [10].

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

В проведенных вычислительных экспериментах высота области G была выбрана равной 30, а длина – 100 (в относительных единицах). Начало декартовой системы координат совпадало с левым нижним углом области моделирования. Центр круга, соответствующего поперечному сечению идеально проводящего цилиндра, вне зависимости от его радиуса совпадал с центром G и имел координаты {x = 15, z = 50}. Были выбраны две точки наблюдения P₁ и P₂ с координатами {x = 15, z = 46.25} и {x = 15, z = 53.75} соответственно, временные зависимости значений компонент поля в которых использовались для нахождения поля рассеяния. Монополярный импульс распространялся от левой границы области G к правой. Таким образом, по отношению к МЭМИ точка P₁ находилась перед препятствием, а P₂ – за ним.

На рис. 2. показаны зависимости магнитной компоненты рассеянного поля, нормированной на амплитуду падающего МЭМИ, в точке наблюдения P₁ от времени для трех значений радиуса цилиндра: 2.5, 1.5 и 0.75. Каждую из этих зависимостей можно условно разделить на три участка, что сделано на примере кривой 1.

Внутри первого временного диапазона (А) форма отраженного сигнала практически повторяет форму падающего. На втором отрезке (В) поле имеет знак, противоположный знаку возбуждающего МЭМИ, и, после достижения минимума, монотонно стремится к нулю. Временная длина этого участка зависит от радиуса цилиндра: чем больше радиус, тем длиннее участок. То есть, временной профиль отраженного импульса на отрезке В формируется в процессе распространения падающего импульса вдоль поверхности цилиндра. Если диаметр неоднородности меньше единицы, то область В практически исчезает и отраженное поле приобретает вид биполярного импульса.

На третьем отрезке времени C рассеянное поле по своей форме приближается к форме исходного МЭМИ и, в итоге, значения поля могут стать снова положительными.

Проведенные вычисления показали, что при радиусе цилиндра >10 область В продолжает увеличиваться, однако величина модуля отрицательных значений в минимуме поля снижается. В итоге при асимптотическом переходе боковой поверхности цилиндра в плоскость отраженное поле приобретает вид моноимпульса, как было показано в [10].

На рис. 3. приведены временные зависимости рассеянного поля в точке P₂. Из кривых 1–3 следует, что для цилиндров с радиусами как больше единицы (2.5, кривая 1), так и меньше (0.75, кривая 3), это поле имеет биполярный вид. Первый полупериод рассеянного поля имеет знак, противоположный знаку подающего МЭМИ.

ЗАКЛЮЧЕНИЕ

Таким образом, полученные результаты дают основание утверждать, что при дифракции монополярного импульса с TM-поляризацией на идеально проводящем цилиндре рассеянное поле всегда оказывается биполярным.

Работа является частью государственного задания ИРЭ им. В.А. Котельникова РАН и поддержана Российским фондом фундаментальных исследований (проект № 19-52-45035-ИНД_a). Моделирование было проведено на вычислительных ресурсах Межведомственного суперкомпьютерного центра РАН.