1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 1, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 85-90

Моделирование структур типа металл–диэлектрик–металл для детектирования терагерцового излучения

К. Т. Ч. Ву 1, *, Г. М. Казарян 1, В. Л. Саввин 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”, Физический факультет
Москва, Россия

* E-mail: kt.vu@physics.msu.ru

Поступила в редакцию 20.07.2020
После доработки 28.08.2020
Принята к публикации 28.09.2020

Полный текст (PDF)

Аннотация

Структуры типа металл–диэлектрик–металл являются перспективным кандидатом на роль эффективного выпрямляющего элемента в терагерцовом диапазоне. Рассматривается численная модель подобной структуры, использующая метод конечных элементов в формализме неравновесной функции Грина.

ВВЕДЕНИЕ

Терагерцевый диапазон является важным объектом исследования в наше время в силу его многочисленных потенциальных применений в медицине, материаловедении, энергетике и других областях. Детектирование излучения в этом диапазоне – сложная задача. Он расположен между микроволновым и инфракрасным диапазоном, методы которых плохо работают для терагерцевых частот. Например, энергия квантов электромагнитного поля, соответствующая этому диапазону, меньше энергии теплового шума при комнатной температуре, что делает применение фотоэлементов неэффективным [1, 2].

В качестве альтернативы были предложения использовать так называемые ректенны [3, 4], т.е. выпрямляющие антенны. Эти устройства представляют собой антенну, соединенную с выпрямляющим элементом. При преобразовании энергии электромагнитной волны в электрический ток эффективность ректенн в микроволновом диапазоне может достигать 70–90% [4, 5]. Их эффективность для более высоких частот является предметом споров. Пессимистичная оценка, полагающая справедливость применения предела Шокли–Квайссера, составляет примерно 30% [6]. Экспериментальные же работы демонстрируют эффективность порядка единиц процентов в лучшем случае. Улучшение этого показателя во многом зависит от нахождения эффективного выпрямляющего элемента.

Большое количество современных исследований предлагают в качестве этого элемента использовать структуры типа металл–диэлектрик–металл. Они, по существу, представляют собой диоды, механизмом переноса заряда в которых является квантовое туннелирование. Теоретически, это позволяет им работать на частотах, достигающих среднего инфракрасного диапазона и, согласно некоторым работам, даже оптического [7–9].

Для структур типа металл–диэлектрик–металл, использующих один слой диэлектрика, было показана невозможность одновременного достижения низкого сопротивления и высокой чувствительности [10]. Предполагается, что применение нескольких диэлектрических слоев или использование асимметричной геометрии их расположения может помочь улучшить эти показатели [10–12]. Эти предложения приводят к существенному усложнению структур, делая их аналитическое рассмотрение очень сложным.

Эта работа посвящена построению численной модели структуры типа металл–диэлектрик–металл с использованием метода конечных элементов в формализме неравновесной функции Грина [13–15]. Метод конечных элементов позволяет строить сетки произвольных форм, что может в перспективе облегчить рассмотрение многомерных структур. Формализм неравновесной функции Грина позволяет получить наиболее детальные сведения о характеристиках структур, что может оказаться чрезвычайно полезным при их анализе.

ПОСТАНОВКА ЗАДАЧИ И МЕТОДОЛОГИЯ

Постановка задачи начинается с определения области Ω, которая состоит из конечной подобласти ΩD и бесконечных подобластей Ωα. Область ${{{\Omega }}_{{\text{D}}}}$ соответствует пространству, заполненному диэлектриками, т.е. расчетной области. Области ${{{\Omega }}_{{\alpha }}}$ соответствуют металлическим проводникам. Для данной энергии E функция Грина $G\left( {\vec {r},~\vec {r}{\kern 1pt} ';E} \right)$ определяется как

(1)
$\left( {E - H} \right)G\left( {\vec {r},\vec {r};E} \right) = \delta \left( {\vec {r} - \vec {r}{\kern 1pt} '} \right),\,\,\,\,\vec {r},~\vec {r}{\kern 1pt} ' \in {\Omega },$
(2)
$H = ~ - \frac{{{{\hbar }^{2}}}}{2}\nabla \left( {\frac{1}{{m\left( {\vec {r}} \right)}}\nabla } \right) + ~V\left( {\vec {r}} \right).$

Здесь H – гамильтониан всей системы, $m\left( {\vec {r}} \right)$ – эффективная масса частицы (электрона в этой задаче), $V\left( {\vec {r}} \right)$ – профиль потенциальной энергии внутри системы, $\delta \left( {\vec {r}} \right)$ – дельта-функция Дирака. Функция Грина полагается равной нулю всюду на границе $\partial {\Omega }$ области Ω и удовлетворяет условиям излучения Зоммерфельда на бесконечности. Задача (1) может быть переписана в виде

(3)
$\left( {E - {{H}^{0}} - ~{\Sigma }} \right)G\left( {\vec {r},\vec {r};E} \right) = \delta \left( {\vec {r} - \vec {r}{\kern 1pt} '} \right),\,\,\,\,\vec {r},~\vec {r}{\kern 1pt} ' \in {{{\Omega }}_{D}},$
где ${{H}^{0}}$ – гамильтониан расчетной области, а Σ описывает взаимодействие проводников и диэлектрической подобласти. Величина Σ называется собственной энергией [13]. Собственная энергия может также учитывать различные взаимодействия частиц внутри расчетной области, но в баллистическом приближении ими можно пренебречь. В этом случае собственную энергию можно представить как сумму собственных энергий ${{{\Sigma }}^{{\alpha }}},$ соответствующих проводникам.

Для решения этой задачи методом конечных элементов ее удобно представить в матричном виде:

(4)
$G\left( E \right) = {{\left( {EI - {{H}^{0}}\left( E \right) - \sum\limits_{\alpha } {{{\sum }^{{\alpha }}}\left( E \right)} } \right)}^{{ - 1}}},$
где I – единичная матрица. Явный вид матриц ${{H}^{0}}$ и ${{\sum }^{{\alpha }}}$ можно получить обычным способом, использующимся в методе конечных элементов, то есть применяя формулу Грина к слабой форме задачи (4):
(5)
$\begin{gathered} \int\limits_{{{{\Omega }}_{D}}} {\left( {E - V\left( {\vec {r}} \right)} \right)G\left( {\vec {r},\vec {r};E} \right)} \phi \left( {\vec {r}} \right)dr - \\ - \,\,\int\limits_{{{{\Omega }}_{D}}} {\frac{{{{\hbar }^{2}}}}{{2m}}} ~\left( {\nabla G\left( {\vec {r},\vec {r};E} \right),\nabla \phi \left( {\vec {r}} \right)} \right)dr - \\ - \,\,\int\limits_{\partial {{{\Omega }}_{D}}} {\frac{{{{\hbar }^{2}}}}{{2m}}} ~\left( {\nabla G\left( {\vec {r},\vec {r};E} \right),~\vec {n}} \right)\,\phi \left( {\vec {r}} \right)ds = \phi \left( {\vec {r}{\kern 1pt} '} \right),\,\,\, \\ \,~\vec {r},~\vec {r}{\kern 1pt} ' \in {{{\Omega }}_{D}}, \\ \end{gathered} $
где $\phi \left( {\vec {r}} \right)$ – пробная функция, $\vec {n}$ – внешняя нормаль к границе $\partial {{{\Omega }}_{D}}.$ На этом этапе следует выбрать базисные функции и разложить по нему все неизвестные величины.
(6)
$\begin{gathered} \phi \left( {\vec {r}} \right) = \sum\limits_p {{{\phi }_{p}}\left( {\vec {r}} \right)} ;\,\,\,\,G\left( {\vec {r},\vec {r}{\kern 1pt} ';E} \right) = \\ = \sum\limits_k {{{G}_{k}}\left( {\vec {r}{\kern 1pt} ';E} \right){{\phi }_{k}}\left( {\vec {r}} \right)} = ~\sum\limits_{k,l} {{{G}_{{k,l}}}\left( E \right)} ~{{\phi }_{l}}\left( {\vec {r}{\kern 1pt} '} \right){{\phi }_{k}}\left( {\vec {r}} \right), \\ \end{gathered} $
где ${{\phi }_{p}}\left( {\vec {r}} \right)$ – базисные функции, которые в простейшем случае выбираются кусочно-линейными, а ${{G}_{{k,l}}}\left( E \right)$ – коэффициенты разложения фунцкии Грина по этому базису.

Подставляя эти выражения в (5) можно получить явные выражения для матриц, используемых в (4):

(7)
$\begin{gathered} H_{{k,l}}^{0} = \int\limits_{{{{\Omega }}_{D}}} {V\left( {\vec {r}} \right){{\phi }_{k}}{{\phi }_{l}}dr} + \int\limits_{{{{\Omega }}_{D}}} {\frac{{{{\hbar }^{2}}}}{{2m}}\nabla {{\phi }_{k}}} \nabla {{\phi }_{l}}dr; \\ E{{S}_{{k,l}}} = \int\limits_{{{{\Omega }}_{D}}} {E{{\phi }_{k}}{{\phi }_{l}}dr} ;\,\,\,\,{{\Sigma }_{{k,l}}} = \int\limits_{\partial {{{\Omega }}_{D}}} {{\Sigma }\left( {\vec {r}} \right){{\phi }_{k}}{{\phi }_{l}}ds} ; \\ \end{gathered} $

Матрица ${{S}_{{k,l}}}$ является своеобразным аналогом единичной матрицы в выбранном базисе.

Собственные энергии соответствуют интегралу по границе в выражении (5), но в то же время требуют знания производной по нормали функции Грина. Для ее нахождения в общем случае требуется решить задачу для вспомогательной функции Грина внутри полубесконечных областей, соответствующих проводникам. В одномерном же случае влияние собственных энергий в контексте метода конечных элементов проявляется в виде граничных условий Робена [13]:

(8)
$\begin{gathered} \int\limits_{\partial {{{\Omega }}_{D}}} {\frac{{{{\hbar }^{2}}}}{{2m}}} \left( {\nabla G\left( {\vec {r},\vec {r};E} \right),~\vec {n}} \right)\phi \left( {\vec {r}} \right)ds = \\ = \sum\limits_{\alpha } {\int\limits_{{{{\Omega }}_{D}}} { - \frac{{i{{\hbar }^{2}}}}{{2{{m}_{\alpha }}}}} } ~\sqrt {\frac{{2{{m}_{{\alpha }}}\left( {E - {{V}_{{\alpha }}}} \right)}}{{{{\hbar }^{2}}}}} G\left( {\vec {r},\vec {r};E} \right)\phi \left( {\vec {r}} \right)ds; \\ {\Sigma }_{{k,l}}^{{\alpha }} = ~\int\limits_{\partial {{{\Omega }}^{{\alpha }}}} { - \frac{{i{{\hbar }^{2}}}}{{2{{m}_{{\alpha }}}}}} \sqrt {\frac{{2{{m}_{{\alpha }}}\left( {E - {{V}_{{\alpha }}}} \right)}}{{{{\hbar }^{2}}}}} {{\phi }_{k}}{{\phi }_{l}}ds, \\ \end{gathered} $
где $\partial {{{\Omega }}^{{\alpha }}}$ – граница раздела между расчетной областью и проводником, mα – эффективная масса электрона в проводнике α, ${{V}_{{\alpha }}}$ – значение потенциала в соответствующем проводнике.

Коэффициент прохождения T(E) и электрический ток J через структуру могут быть найдены из выражений

(9)
$\begin{gathered} T\left( E \right) = ~\,{\text{tr}}\left( {{{\Gamma }^{1}}G{{\Gamma }^{2}}{{G}^{ + }}} \right);\,\,\,\,{{\Gamma }^{{\alpha }}} = ~ - i\left( {{{\Sigma }^{{\alpha }}} - {{\Sigma }^{{{\alpha + }}}}} \right); \\ ~\alpha = 1,2,\,\,\,\,J = \frac{e}{{\pi \hbar }}\int\limits_{ - \infty }^\infty {T\left( E \right)} \left( {{{f}_{{FD}}}\left( {E - {{\mu }_{1}}} \right) - } \right. \\ \left. { - \,\,~{{f}_{{FD}}}\left( {E - {{\mu }_{2}}} \right)} \right)dE, \\ \end{gathered} $
где e – заряд электрона, ${{\Gamma }^{{\alpha }}}$ – диссипативная функция уширения, ${{\mu }_{{\alpha }}}$ – химический потенциал соответствующего проводника, ${{f}_{{FD}}}\left( E \right)$ – функция распределения Ферми–Дирака. Верхний индекс + обозначает эрмитово сопряжение. Для удобства можно принять уровень энергии Ферми одного из проводников равным нулю и отсчитывать все энергии от него. Таким образом, выражение для плотности тока можно переписать в виде
(10)
$J = \frac{e}{{\pi \hbar }}\int\limits_{ - \infty }^\infty {T\left( E \right)} \left( {{{f}_{{FD}}}\left( E \right) - ~{{f}_{{FD}}}\left( {E - e{{V}_{b}}} \right)} \right)dE,$
где ${{V}_{b}}$ – напряжение смещения между проводниками.

Следует отметить, что в силу характера распределения Ферми–Дирака лишь конечный диапазон энергий вносит существенный вклад в выражение (10). Особое внимание следует также уделить пикам коэффициента пропускания $T\left( E \right),$ приходящимся на упомянутый диапазон. Эти пики могут быть учтены путем применения адаптивного шага дискретизации по энергии, как в работе [10], или через следующую задачу на собственные значения

(11)
$\begin{gathered} {{H}^{0}}\psi \left( {\vec {r}} \right) = ~E\psi \left( {\vec {r}} \right),\,\,\,\,\vec {r} \in {{{\Omega }}_{D}}, \\ \psi \left( {\vec {r}} \right) = 0,\,\,\,\,\vec {r} \in \partial {{{\Omega }}_{D}}~. \\ \end{gathered} $

Эта задача также может быть решена численно. Профиль потенциального барьера может быть представлен как

(12)
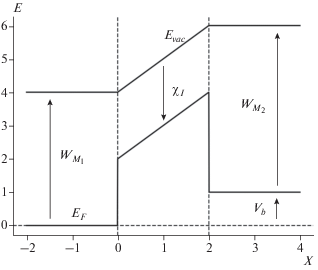
$V\left( {\vec {r}} \right) = ~{{V}_{0}}\left( {\vec {r}} \right) + ~{{U}_{0}}\left( {\vec {r}} \right),\,\,\,\,\vec {r} \in {{{\Omega }}_{D}},$
где ${{U}_{0}}$ – внешний приложенный потенциал, а ${{V}_{0}}$ – профиль потенциала в структуре в отсутствие смещения. Потенциал ${{V}_{0}}$ может быть получен из характеристик материалов, если допустить, что все электроны перемещаются по зонам проводимости (рис. 1).

Рис. 1.

Профиль потенциального барьера в структуре типа металл–диэлектрик–металл. Область внутри пунктирных вертикальных линий соответствует диэлектрическому слою. ${{E}_{F}}$ – уровень энергии Ферми металлов, ${{E}_{{{v}ac}}}$ – уровень энергии вакуума, ${{W}_{{{{M}_{{1,2}}}}}}$ – работы выхода соответствующих металлов, ${{\chi }_{I}}$ – сродство к электрону для данного диэлектрика, ${{V}_{b}}$ – приложенное напряжение, x – условная координата.

Приложенный потенциал ${{U}_{0}}$ удовлетворяет уравнению Пуассона

(13)
$\nabla \left( {{{\varepsilon }_{0}}\varepsilon \left( {\vec {r}} \right)\nabla \left( {{{U}_{0}}\left( {\vec {r}} \right)} \right)} \right) = ~en\left( {\vec {r}} \right),\,\,\,\,\vec {r} \in {{{\Omega }}_{D}},$
где $n\left( {\vec {r}} \right)$ – плотность заряда в структуре, ${{\varepsilon }_{0}}$ – диэлектрическая постоянная, а ε – относительная диэлектрическая проницаемость. В одномерном случае при учете потенциала зарядов-изображений выражение для потенциала приобретает вид [13]:
(14)
$\begin{gathered} V\left( x \right) = ~{{V}_{0}}\left( x \right) + {{U}_{0}}\left( x \right) - \frac{{{{e}^{2}}}}{{16\pi {{\varepsilon }_{0}}}} \times \\ \times \,\,\left( {\frac{1}{{\int\limits_0^x {\varepsilon \left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} }} + \frac{1}{{\int\limits_x^L {\varepsilon \left( {x{\kern 1pt} '} \right)dx{\kern 1pt} '} }}} \right), \\ \end{gathered} $
где x – координата внутри области расчета, L – длина структуры.

Если зарядов внутри структуры нет, задача – одномерна, а диэлектрическая проницаемость имеет кусочно-постоянный характер, то выражение для потенциала можно получить аналитически. В этой работе для сохранения общности подхода задача для потенциала решалась численно, методом конечных элементов.

Расчеты производились с использованием вычислительной платформы FEniCS. С ее помощью решалась задача для потенциала и получались матричные выражения для нахождения функции Грина. Описание компонентов платформы можно найти в [16–21].

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Модель была протестирована на двух задачах, имеющих хорошо известное решение: задача о туннелировании через прямоугольный потенциальный барьер и задача о туннелировании через барьер-ступеньку. Полученный при моделировании коэффициент прохождения сравнивался с точными выражениями при одних и тех же значениях энергии. Для оценки ошибки вычислений используется следующая формула [22 ] :

(15)
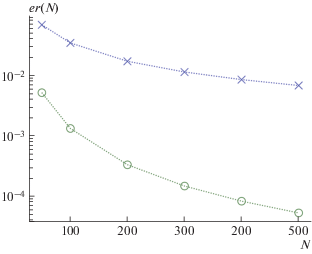
$er\left( N \right) = \,\,~\mathop {\max }\limits_E \left| {T\left( E \right) - ~{{T}_{0}}\left( E \right)} \right|,$
где N – число узлов в сетке, $T\left( E \right)$ – полученный при моделировании коэффициент прохождения, ${{T}_{0}}\left( E \right)$ – точное выражение для коэффициента прохождения для данного барьера, а значение энергии E ограничено величинами, использованными при моделировании. Результаты представлены на рис. 2.

Рис. 2.

Зависимость метрики ошибки $er\left( N \right)$ от числа узлов в сетке пространственного разбиения N для тестовых задач: прямоугольный потенциальный барьер (крестики), барьер-ступенька (кружки).

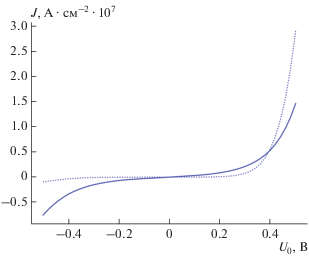
Также было проведено сравнение между результатами, полученными от данной модели, и данными работы [12] для структур W–Nb2O5 (1 нм)–Ta2O5–(1 нм)–W и W–Nb2O5 (3 нм)–Ta2O5 (1 нм)–W. Последняя структура характеризуется как резонансная. Полученные для этих структур вольт-амперные характеристики представлены на рис. 3. Они хорошо согласуются с известными данными.

Рис. 3.

Полученные зависимости плотности тока $J$ от приложенного напряжения ${{U}_{0}}$ для структур металл–диэлектрик–металл с учетом потенциала зарядов изображений. Сплошная линия – структура W–Nb2O5 (1 нм)–Ta2O5–(1 нм)–W, пунктирная – W–Nb2O5 (3 нм)–Ta2O5–(1 нм)–W.

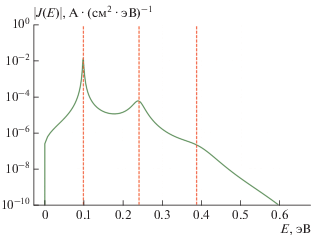
Можно также показать, что пики зависимости коэффициента пропускания и плотности тока от энергии для резонансной структуры соответствует собственным значениям задачи (11), как видно на рис. 4.

Рис. 4.

Абсолютная величина распределения электрического тока $\left| {~J\left( E \right)~} \right|$ по энергии E для резонансной структуры при фиксированном напряжении смещения 0.5 В. Вертикальные пунктирные линии отмечают собственные значения гамильтониана расчетной области ${{H}^{0}}$.

ЗАКЛЮЧЕНИЕ

В данной работе была представлена одномерная модель переноса заряда посредством квантового туннелирования в структурах типа металл–диэлектрик–металл, использующая метод конечных элементов и формализм неравновесной функции Грина. Модель была проверена на тестовых задачах. Полученные при моделировании результаты хорошо соответствуют известным для этих задач решениям.

Замечено, что задача на собственные значения, связанная с профилем потенциального барьера, может дать приблизительные энергии пиков зависимости коэффициента пропускания от энергии электронов. Эта информация может помочь сделать расчеты более точными и производительными, например, путем сокращения количества разбиений диапазона энергий, для которого производятся вычисления.

Модель также может быть расширена на большее число пространственных измерений без существенных изменений в постановке задачи. Как показано в работе [13], собственные энергии металлических контактов могут быть выражены через собственные функции подводящих проводов, например, представляя их в виде полубесконечных полос. При этом вычислительная сложность должна резко вырасти, поскольку такой характер имеют часто используемые в данной модели матричные операции. Правильная дискретизация диапазона энергии, используемого в расчете, может помочь сохранить точность и замедлить рост требуемых вычислительных ресурсов.

Список литературы

  1. Shank J., Kadlec E.A., Jarecki R.L. et al. // Phys. Rev. Appl. 2018. V. 9. Art. No 054040.

  2. Zhu Z., Joshi S., Moddel G. // IEEE J. Sel. Top. Quant. 2014. V. 20. Art. No 3801409.

  3. Bailey R. // J. Eng. Power. 1972. V. 94. P. 73.

  4. Shinohara N. // IEICE Electron. Expr. 2013. V. 10. Art. No 20132009.

  5. Douyère A., Lan Sun Luk J.D., Alicalapa F. // Electron. Lett. 2008. V. 44. P. 1409.

  6. Joshi S., Moddel G. // J. Phys. D. 2016. V. 49. Art. No 265602.

  7. Mitrovic I.Z., Weerakkody A.D., Sedghi N. et al. // Appl. Phys. Lett. 2018. V. 112. Art. No 012902.

  8. Hartman T.E. // J. Appl. Phys. 1962. V. 33. Art. No 3427.

  9. Moddel G., Grover S. Rectenna solar cells. N.Y.: Springer, 2013.

  10. Shin J.H., Yang J.H., Heo S.J., Jang J.E. // AIP Adv. 2017. V. 7. Art. No 105307.

  11. Grover S., Moddel G. // Sol. St. Electron. 2012. V. 67. P. 94.

  12. Jiang H., Shao S., Cai W., Zhang P. // J. Comput. Phys. 2008. V. 227. P. 6553.

  13. Havu P., Havu V., Puska M.J., Nieminen R.M. // Phys. Rev. B. 2004. V. 69. Art. No 115325.

  14. Polizzi E., Datta S. // Proc. Third IEEE Conf. Nanotechnol (San Francisco, 2003). V. 2. P. 40.

  15. Alnaes M.S., Blechta J., Hake J. et al. // Arch. Numer. Software. 2015. V. 3. Art. No 20553.

  16. Logg A., Mardal K.-A., Wells G.N. et al. Automated solution of differential equations by the finite element method. Springer, 2012.

  17. Kirby R.C., Logg A. // ACM Transact. Math. Software. 2011. V. 32. No 3. P. 417.

  18. Alnaes M.S., Logg A., Olgaard K. et al. // ACM Transact. Math. Software. 2014. V. 40. P. 1.

  19. Kirby R.C. // ACM Transact. Math. Software. 2004. V. 30. P. 502.

  20. Alnaes M.S., Logg A., Mardal K.-A. et al. // Inter. J. Comp. Sci. Engin. 2009. V. 4. No 4. P. 231.

  21. Abdolkader T.M., Shaker A., Alahmadi A.N.M. // Eur. J. Phys. 2018. V. 39. No 4. Art. No 045402.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал