Известия РАН. Серия физическая, 2021, T. 85, № 11, стр. 1542-1545

Изучение взаимодействия спиновых волн с периодическими магнитными решетками, называемыми также слабоконтрастными магнонными кристаллами, было начато в работах [1–3], где экспериментально исследовались эффекты взаимодействия волн с магнонными кристаллами при брэгговской [1, 3] или раман-натовской [2] дифракции, а также амплитудные характеристики волн при прохождении через кристалл или отражении от него. В работе [3] на основе методов вторичного квантования была построена теория брэгговской дифракции поверхностных спиновых волн на слабом возмущающем потенциале магнонного кристалла. Более подробно эта теория изложена в работе [4].

В продолжение этих исследований в работе [5] методом подвижного зонда были измерены дисперсионные характеристики магнонного кристалла на основе структуры металл–диэлектрик–феррит, помещенной в пространственно-периодическое магнитное поле. Обнаружено свойство невзаимности магнонного кристалла, которое проявляется в различии дисперсионных характеристик волн, распространяющихся в противоположных направлениях.

В дальнейшем метод подвижного зонда был усовершенствован, в частности, были разработана методика, позволяющая визуализировать многочастотные распределения комплексных амплитуд спиновых волн по всей поверхности пленочного ферритового образца (подробнее указанный метод и экспериментальная установка описаны в [6]). Ниже представлены полученные на основе данной методики результаты экспериментов и соответствующие расчеты по исследованию дифракции поверхностных спиновых волн (ПСВ) на слабоконтрастном магноном кристалле.

При проведении экспериментов использовалась пленка железоиттриевого граната (ЖИГ) толщиной s = 13.9 мкм и намагниченностью насыщения 4πM₀ = 1868 Гс. Пленка ЖИГ была касательно намагничена внешним однородным магнитным полем величиной H₀ = 460 Э. Пространственно-периодическое магнитное поле создавалось на части пленки ЖИГ четырьмя отрезками магнитофонной ленты, расположенными на поверхности пленки ЖИГ параллельно друг другу, так что общая ширина магнонного кристалла составляла 15 мм. Для совмещения максимумов записанных на ленту синусоидальных сигналограмм использовался метод визуализации магнитных доменов, наведенных магнитофонной записью, по наблюдаемому фарадеевскому вращению (подробнее этот метод описан в [7]).

Предварительные расчеты показали, что если при указанных параметрах расположить возбуждающий линейный преобразователь под углом 45° к вектору магнитного поля $\overrightarrow {{{H}_{0}}} ,$ то волновые пучки ПСВ с различными частотами будут похожи на сверхнаправленные лучи с малой дифракционной расходимостью [8–11], причем такая геометрия одновременно обеспечит и режим брэгговской дифракции на частотах около 3000 МГц.

Распределение СВЧ поля ПСВ измерялось методом зондирования поверхности ферритовой пленки в двух взаимно перпендикулярных направлениях вдоль осей Y и Z, причем ось Z совпадала с направлением вектора $\overrightarrow {{{H}_{0}}} .$ На рис. 1а и 2а представлены экспериментальные визуализированные СВЧ поля волновых пучков ПСВ с малой дифракционной расходимостью при их дифракции на магнонном кристалле, у которого вектор решетки $\vec {q}$ ориентирован параллельно вектору $\overrightarrow {{{H}_{0}}} .$ На основе предварительных расчетов период решетки кристалла был выбран равным T = 810 мкм, что позволило обеспечить подходящие условия для возникновения брэгговской дифракции при падении на кристалл сверхнаправленного луча ПСВ [11]. Поскольку как сверхнаправленное распространение, так и возникновение брэгговской дифракции существенно зависят от волнового числа и частоты ПСВ, то при небольшом изменении частоты волны в пределах ~100 МГц в эксперименте наблюдался ряд совершенно разных дифракционных картин, на которых прохождение луча ПСВ через магнонный кристалл сопровождалось появлением множества смещенных лучей с тем же направлением распространения и множества продифрагироваших лучей с зеркально-симметричным относительно оси Y направлением распространения. Экспериментальные дифракционные картины (подробно описанные в [12, 13]), представленные на рис. 1а и 2а, зависели от частоты и направления вектора решетки $\vec {q},$ определявшего параметры прошедшей волны, количество лучей, их направления и амплитуды. На рис. 1а и 2а магнонный кристалл схематично изображен в виде вертикальной полосы, заполненной чередующимися полосками с периодом 810 мкм, а цветовая гамма распределения ПСВ соответствует увеличению амплитуды ПСВ от синего (малая амплитуда) до красного (большая амплитуда).

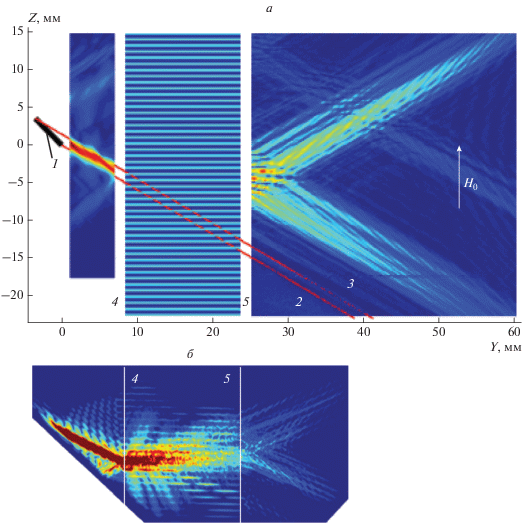
Рис. 1.

Экспериментальная (а) и рассчитанные (б) картины распределения амплитуды ПСВ с частотой 2960 МГц при ее дифракции на слабоконтрастном магноном кристалле. 1 – возбуждающий ПСВ линейный преобразователь длиной 5 мм; 2 и 3 – условные границы сверхнаправленного луча ПСВ при отсутствии магнонного кристалла; 4 и 5 – границы магнонного кристалла.

Расчеты, соответствующие приведенным на рис. 1а и 2а экспериментальным дифракционным картинам ПСВ, были выполнены на базе пакета программ MUMAX3 с помощью методики микромагнитного моделирования и представлены на рис. 1б и 2б. Распределения амплитуды или интенсивности ПСВ (рис. 1б и 2б) были рассчитаны методом конечных разностей на основе уравнения Ландау-Лифшица с диссипативным членом в форме, предложенной Гильбертом, причем при расчетах параметр диссипации был выбран равным 10^–5. Отметим, что использование указанной методики, позволило получить двумерные картины распределения амплитуды ПСВ как за пределами области магнонного кристалла, так и в области пленки, образующей магнонный кристалл.

В наибольшей степени режиму брэгговской дифракции соответствует картина, представленная на рис. 1а, на которой виден узкий, хорошо сформированный, сверхнаправленный падающий луч слева от магнонного кристалла.

Справа от кристалла наблюдаются два луча, распространяющиеся в разные стороны относительно оси Y – прошедший основной луч нулевого порядка дифракции и продифрагировавший брэгговский луч первого порядка. Отметим, что основной луч оказался сдвинутым вверх относительно исходного падающего луча и оба прошедших луча за счет взаимодействия с периодической структурой кристалла оказались значительно шире падающего луча.

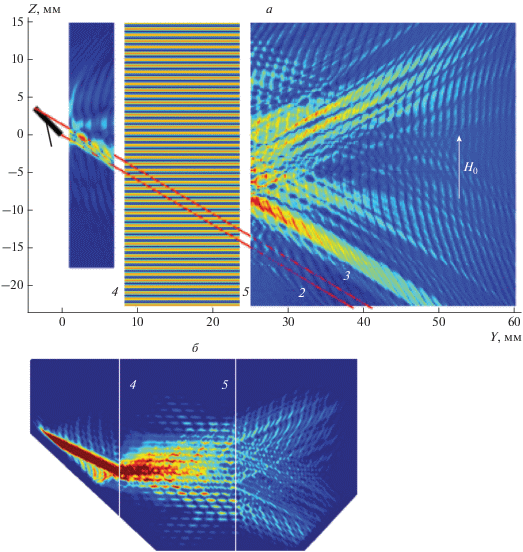
При небольшом увеличении частоты ПСВ для основной части падающего луча условия брэгговской дифракции перестают выполняться, но поскольку дифракционная расходимость падающего луча с увеличением частоты тоже возрастает (а это означает, что энергии луча оказывается распределена по более широкому интервалу волновых чисел, каждому из которых соответствует свой угловой сектор внутри расходящегося луча), то для некоторого углового сектора луча выполнение условия брэгговской дифракции все еще сохраняется. Так, например, при частоте ПСВ f = = 3056 МГц (рис. 2) на большей части пленки ЖИГ, расположенной справа от кристалла, наблюдаются узкие дифракционные лучики, так называемые дублеры лучей первого и второго порядка дифракции (возникновение и развитие которых с изменением частоты подробнее описано в [12, 13]). Следует отметить, что поскольку исходный луч ПСВ, падающий на магнонный кристалл, обладает сверхнаправленными свойствами, то и все возникающие лучи-дублеры также обладают этим свойством (несмотря на то, что они гораздо уже исходного луча) и характеризуются малой дифракционной расходимостью: как видно из рис. 2 они практически не расплываются по мере распространения как на экспериментальной, так и на рассчитанной дифракционных картинах. Кроме того, Фурье-анализ экспериментального распределения ПСВ (подробнее описанный в [14]), проведенный для области, где наблюдаются лучи-дублеры, показал, что волновое число каждого луча-дублера отличается от волнового числа соседнего луча-дублера на несколько обратных сантиметров.

Рис. 2.

Экспериментальная (а) и рассчитанные (б) картины распределения амплитуды ПСВ с частотой 3056 МГц при ее дифракции на слабоконтрастном магноном кристалле. 1 – возбуждающий ПСВ линейный преобразователь длиной 5 мм; 2 и 3 – условные границы сверхнаправленного луча ПСВ при отсутствии магнонного кристалла; 4 и 5 – границы магнонного кристалла.

Работа выполнена за счет бюджетного финансирования в рамках государственного задания по теме № 0030-2019-0014 и при частичной финансовой поддержке Российского фонда фундаментальных исследований (проект № 20-07-00356).