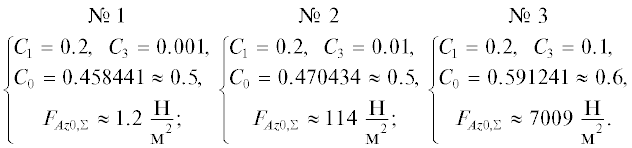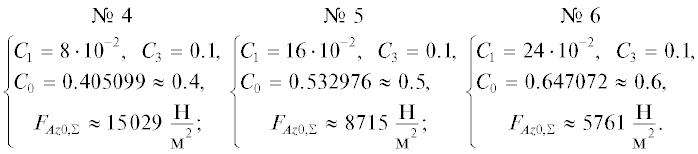Известия РАН. Серия физическая, 2021, T. 85, № 11, стр. 1568-1572

Взаимодействие неоднородного постоянного магнита, состоящего из решетки магнитожестких полосок, с массивной ферромагнитной средой

М. А. Пятаков¹, М. Л. Акимов^1, *, П. А. Поляков¹

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

^* E-mail: ml.akimov@physics.msu.ru

Поступила в редакцию 21.06.2021
После доработки 05.07.2021
Принята к публикации 28.07.2021

DOI: 10.31857/S0367676521110314

Полный текст (PDF)

Аннотация

Разработана теория и получена общая аналитическая формула для силы взаимодействия решетки из намагниченных полосок с произвольными параметрами. Сделан анализ закономерности силы взаимодействия магнитной решетки с массивным ферромагнетиком в зависимости от толщины, ширины полоски и расстояния от решетки до ферромагнетика в самом общем случае.

ВВЕДЕНИЕ

Исследование постоянных магнитов актуально, и обусловлено необходимостью выявления закономерностей их взаимодействий с материалами, а также технологическими вопросами практического использования [1]. Проводятся исследования того, как размер, форма, поперечное сечение магнита влияют на характеристики магнитного поля и эффективность его применения в технике [2–4]. Выбор электродвигателя с требуемыми характеристиками может повысить быстродействие, следовательно, и производительность всей силовой установки. В технике зачастую применяются многослойные тонкие магниты – пленочные материалы, имеющие слоистую структуру [2, 5].

Цель данной работы заключается в анализе пондеромоторной силы взаимодействия тонких пленочных постоянных магнитов с массивным ферромагнетиком в зависимости от различных параметров. Это является важным для увеличения оптимальной силы взаимодействия существующих неоднородных магнитных материалов. В статье [6] проведены подобные исследования в дипольном приближении, что накладывает дополнительные ограничения на характеристики системы. В работе исследования проводятся методом изображений, разрабатывается общая теория и выводится общая аналитическая формула для силы взаимодействия решетки из намагниченных полосок с произвольными параметрами.

ПОСТАНОВКА ЗАДАЧИ

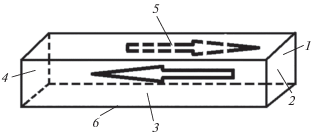
Возьмем отдельную полоску (см. рис. 1), которая однородно намагничена перпендикулярно ее верхней плоскости. Пусть вектор намагниченности $\vec {M}$, тогда магнитное поле, которое порождается данным однородным распределением намагниченности, эквивалентно магнитному полю от эффективных молекулярных токов с поверхностной плотностью $J = \left| {\vec {M}} \right|,$ которые циркулируют по боковым граням полоски [7].

Рис. 1.

Токи Ампера на поверхности пленочного материала.

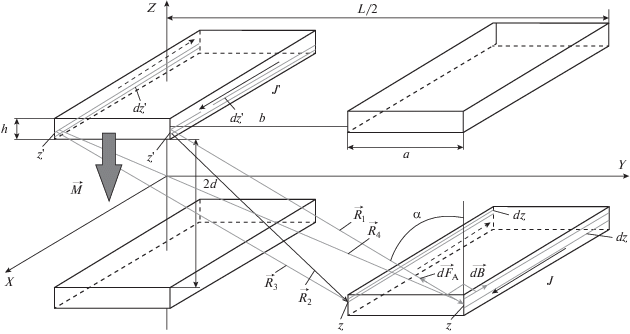
Полоски бесконечно длинные, поэтому влиянием молекулярных токов от граней 2 и 4 (рис. 1) пренебрегаем. Согласно методу изображений рассматривается взаимодействие двух решеток – полосок и их магнитостатических изображений – относительно плоской границы поверхности ферромагнетика (листа). На рис. 2 отражены параметры системы: характерный размер равен L (справа и слева от вертикали L/2), расстояние между решетками составляет 2d, ширина каждой полоски равна a, толщина – h, расстояние между соседними полосками – b, количество пленок по одну сторону от вертикали равно N (всего 2N + 1). Центральной полоске присваивается нулевой номер, и рассматривается сила, с которой решетка полосок притягивает решетку изображений.

Рис. 2.

Система из двух решеток.

Величину индукции $dВ$ магнитного поля линейного тока узкой полоски ширины $dz{\kern 1pt} '$ на расстоянии R легко получить, используя теорему о циркуляции [7]:

(1)

$dB = \frac{{{{{{\mu }}}_{{\text{0}}}}J{\kern 1pt} 'dz{\kern 1pt} '}}{{2{{\pi }}R}},$

где $J{\kern 1pt} ' = J = M.$ Тогда выражение для силы взаимодействия Ампера двух линейных токов шириной $dz{\kern 1pt} '$ и $dz$ имеет вид

(2)

$d{{F}_{A}} = JdzdB = \frac{{{{{{\mu }}}_{0}}{{M}^{2}}dzdz{\kern 1pt} '}}{{2{{\pi }}R}},$

а для проекции на вертикальную ось z силы в соответствии с формулой (2) получим (“±” перед формулой определяет знак проекции, см. рис. 2)

(3)

$\begin{gathered} d{{F}_{{Az}}} = \pm d{{F}_{A}}\cos \alpha = \pm d{{F}_{A}}\frac{{\left| {z{\kern 1pt} ' - z} \right|}}{R} = \\ = \pm \frac{{{{\mu }_{0}}{{M}^{2}}dz{\kern 1pt} 'dz}}{{2\pi R}}\frac{{\left| {z{\kern 1pt} ' - z} \right|}}{R}. \\ \end{gathered} $

Если рассмотреть взаимодействие четырех линейных токов, текущих по боковым граням двух полосок (рис. 2), принимая во внимание (3), мы можем получить суммарную проекцию силы Ампера со стороны полоски, расположенной вдоль оси x (нулевой полоски), на изображение под номером n. Получим формулу (4):

(4)

$\begin{gathered} {{F}_{{Az0,n}}} = \frac{{{{\mu }_{0}}{{M}^{2}}}}{{2\pi }}a\int\limits_0^{{{C}_{3}}} {d{{t}_{1}}} \int\limits_0^{{{C}_{3}}} {d{{t}_{2}}} \times \\ \times \,\,\left[ {2\frac{{{{t}_{1}} + {{t}_{2}} + {{C}_{1}}}}{{{{{\left( {n{{C}_{2}}} \right)}}^{2}} + {{{\left( {{{t}_{1}} + {{t}_{2}} + {{C}_{1}}} \right)}}^{2}}}} - } \right. \\ - \,\,\frac{{{{t}_{1}} + {{t}_{2}} + {{C}_{1}}}}{{{{{\left( {n{{C}_{2}} - 1} \right)}}^{2}} + {{{\left( {{{t}_{1}} + {{t}_{2}} + {{C}_{1}}} \right)}}^{2}}}} - \\ - \,\,\left. {\frac{{{{t}_{1}} + {{t}_{2}} + {{C}_{1}}}}{{{{{\left( {n{{C}_{2}} + 1} \right)}}^{2}} + {{{\left( {{{t}_{1}} + {{t}_{2}} + {{C}_{1}}} \right)}}^{2}}}}} \right], \\ \end{gathered} $

где выполнена замена ${{t}_{1}}\, = \frac{{z{\kern 1pt} ' - d}}{a},$ ${{t}_{2}}\, = \frac{{ - z - d}}{a},$ ${{C}_{1}} = \frac{{2d}}{a},$ ${{C}_{2}} = 1 + \frac{b}{a},$ ${{C}_{3}} = \frac{h}{a}.$

РЕЗУЛЬТАТЫ

Путем прямого взятия двойных интегралов, фигурирующих в (4), получено общее выражение для безразмерной поверхностной плотности z-компоненты силы взаимодействия нулевой полоски с изображениями всех полосок $F_{{Az0,\Sigma }}^{{{\text{безразмерная,}}\,\,{\text{на}}\,\,{\text{ед}}{\text{.}}\,\,{\text{площади}}}}{\text{:}}$

(5)

$\begin{gathered} F_{{Az0,\Sigma }}^{{{\text{безразмерная,}}\,\,{\text{на}}\,\,{\text{ед}}{\text{.}}\,\,{\text{площади}}}} \cdot 2\frac{a}{{\pi \left( {a + b} \right)}} = 2\frac{a}{{\pi \left( {a + b} \right)}}\sum\limits_{n = 1}^N {\left\{ {{{C}_{3}}\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + 2{{C}_{3}}} \right)}}^{2}} + {{n}^{2}}C_{2}^{2}}}{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + {{n}^{2}}C_{2}^{2}}}} \right] + } \right.} \\ + \,\,\left( {{{C}_{1}} + {{С}_{3}}} \right)\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + 2{{C}_{3}}} \right)}}^{2}} + {{n}^{2}}C_{2}^{2}}}{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + {{n}^{2}}C_{2}^{2}}}} \right] + \,\,2n{{С}_{2}}\operatorname{arctg} \left[ {\frac{{{{C}_{1}} + 2{{C}_{3}}}}{{n{{C}_{2}}}}} \right] - 2n{{C}_{2}} \times \\ \times \,\,\operatorname{arctg} \left[ {\frac{{{{C}_{1}} + {{C}_{3}}}}{{n{{C}_{2}}}}} \right] - 2n{{C}_{2}}arctg\left[ {\frac{{{{C}_{1}} + {{C}_{3}}}}{{n{{C}_{2}}}}} \right] + \,\,2n{{C}_{2}}\operatorname{arctg} \left[ {\frac{{{{C}_{1}}}}{{n{{C}_{2}}}}} \right] - {{C}_{1}} \times \\ \times \,\,\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + {{n}^{2}}C_{2}^{2}}}{{C_{1}^{2} + {{n}^{2}}C_{2}^{2}}}} \right] - \frac{1}{2}{{C}_{3}}\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + 2{{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} + 1} \right)}}^{2}}}}{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} + 1} \right)}}^{2}}}}} \right] - \frac{1}{2}\left( {{{С}_{1}} + {{С}_{3}}} \right) \times \\ \times \,\,\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + 2{{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} + 1} \right)}}^{2}}}}{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} + 1} \right)}}^{2}}}}} \right] - \left( {n{{C}_{2}} + 1} \right)\operatorname{arctg} \left[ {\frac{{{{C}_{1}} + 2{{C}_{3}}}}{{n{{C}_{2}} + 1}}} \right] + 2\left( {n{{C}_{2}} + 1} \right)\operatorname{arctg} \left[ {\frac{{{{C}_{1}} + {{C}_{3}}}}{{n{{C}_{2}} + 1}}} \right] - \\ - \,\,\left( {n{{C}_{2}} + 1} \right)\operatorname{arctg} \left[ {\frac{{{{C}_{1}}}}{{n{{C}_{2}} + 1}}} \right] + \,\,\frac{1}{2}{{C}_{1}}\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} + 1} \right)}}^{2}}}}{{C_{1}^{2} + {{{\left( {n{{C}_{2}} + 1} \right)}}^{2}}}}} \right] - \\ - \,\,\frac{1}{2}{{C}_{3}}\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + 2{{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} - 1} \right)}}^{2}}}}{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} - 1} \right)}}^{2}}}}} \right] - \,\,\frac{1}{2}\left( {{{С}_{1}} + {{С}_{3}}} \right)\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + 2{{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} - 1} \right)}}^{2}}}}{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + {{{\left( {n{{C}_{2}} - 1} \right)}}^{2}}}}} \right] - \\ - \,\,\left( {{{C}_{1}} + {{C}_{3}}} \right)ln\left[ {\frac{{{{C}_{1}} + {{C}_{3}}}}{{{{C}_{1}}}}} \right] + \left( {{{C}_{1}} + 2{{C}_{3}}} \right)\,ln\left( {\frac{{{{C}_{1}} + 2{{C}_{3}}}}{{{{C}_{1}} + {{C}_{3}}}}} \right) - \frac{1}{2}{{C}_{3}}\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + 2{{C}_{3}}} \right)}}^{2}} + 1}}{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + 1}}} \right] - \\ - \,\,\frac{1}{2}\left( {{{С}_{1}} + {{С}_{3}}} \right)\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + 2{{C}_{3}}} \right)}}^{2}} + 1}}{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + 1}}} \right] - \,\,\operatorname{arctg} \left[ {{{C}_{1}} + 2{{C}_{3}}} \right] + 2\operatorname{arctg} \left[ {{{C}_{1}} + {{C}_{3}}} \right] - \\ - \,\,\operatorname{arctg} \left[ {{{C}_{1}}} \right] + \frac{1}{2}{{C}_{1}}\ln \left[ {\frac{{{{{\left( {{{C}_{1}} + {{C}_{3}}} \right)}}^{2}} + 1}}{{C_{1}^{2} + 1}}} \right]. \\ \end{gathered} $

Множитель перед суммой в (5) представим следующим образом:

(6)

$2\frac{a}{{\pi \left( {a + b} \right)}} = \frac{2}{{\pi \left( {1 + \frac{b}{a}} \right)}} = \frac{2}{{\pi \left( {1 + {{C}_{0}}} \right)}},\,\,\,\,{{С}_{0}} \equiv \frac{b}{a}.$

По формуле (5) с учетом (6) построены зависимости поверхностной плотности силы от параметров системы. Рассмотрим следующие случаи. Пусть

(7)

$\begin{gathered} a = 1\,\,{\text{мм}} = {{10}^{{ - 3}}}\,\,{\text{м}},\,\,\,\,d = h = 1\,\,{\text{мкм}} = {{10}^{{ - 6}}}\,\,{\text{м,}} \\ 0 \leqslant {{С}_{0}} \leqslant 0.1,\,\,\,\,{{C}_{1}} = 2\frac{d}{a} = 0.002,\,\,\,\,{{C}_{3}} = \frac{h}{a} = 0.001. \\ \end{gathered} $

Зависимость показана на рис. 3а. Безразмерное и размерное (оценка везде по неодим-железо-бору) значения максимума силы, а также расстояние между полосками, при котором реализуется максимум, оказались следующими:

(8)

$\begin{gathered} F_{{Az0,\Sigma }}^{{{\text{безразмерная,}}\,\,{\text{на}}\,\,{\text{ед}}{\text{.}}\,\,{\text{площади}},\,\,max}} \approx 0.00021, \\ {{C}_{0}} \approx {\text{0}}{\text{.026,}} \\ F_{{Az0,\Sigma }}^{{{\text{безразмерная,}}\,\,{\text{на}}\,\,{\text{ед}}{\text{.}}\,\,{\text{площади}},\,\,max}} \cdot \frac{2}{{\pi \left( {1 + {{C}_{0}}} \right)}} \cdot \frac{{{{{{\mu }}}_{0}}{{M}^{2}}}}{2} \approx 140\,\,\frac{{\text{Н}}}{{{{{\text{м}}}^{{\text{2}}}}}}. \\ \end{gathered} $

Рис. 3.

Зависимость безразмерной z-компоненты силы взаимодействия нулевой полоски со всеми изображениями, приходящейся на единицу площади, при различных значениях параметров.

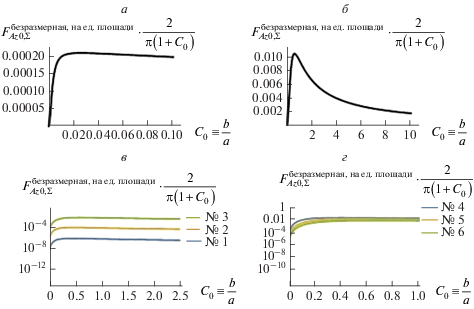
Пусть теперь параметры системы

(9)

$\begin{gathered} a = 1\,\,{\text{мм}} = {{10}^{{ - 3}}}\,\,{\text{м}},\,\,\,\,d = h = 100\,\,{\text{мкм}} = {{10}^{{ - 4}}}\,\,{\text{м}}, \\ 0 \leqslant {{С}_{0}} \leqslant 10,\,\,\,\,{{C}_{1}} = 2\frac{d}{a} = 0.2,\,\,\,\,{{C}_{3}} = \frac{h}{a} = 0.1. \\ \end{gathered} $

Соответствующая зависимость показана на рис. 3б.

Безразмерное и размерное значения максимума силы, а также расстояние между полосками, при котором реализуется максимум, оказались теперь такими:

(10)

$\begin{gathered} F_{{Az0,\Sigma }}^{{{\text{безразмерная,}}\,\,{\text{на}}\,\,{\text{ед}}{\text{.}}\,\,{\text{площади}},\,\,max}} \approx {\text{0}}{\text{.010}},\,\,\,\,{{C}_{0}} \approx {\text{0}}{\text{.6,}} \\ F_{{Az0,\Sigma }}^{{{\text{безразмерная,}}\,\,{\text{на}}\,\,{\text{ед}}{\text{.}}\,\,{\text{площади}},\,\,max}} \cdot \frac{2}{{\pi \left( {1 + {{C}_{0}}} \right)}} \cdot \frac{{{{{{\mu }}}_{0}}{{M}^{2}}}}{2} \approx {\text{7009}}\,\,\frac{{\text{Н}}}{{{{{\text{м}}}^{{\text{2}}}}}}. \\ \end{gathered} $

Таким образом, при увеличении расстояния до ферромагнетика и толщины полоски в 100 раз, наблюдается увеличение силы в 50 раз. Оптимальным набором параметров системы среди представленных двух является тот, в котором расстояние до ферромагнетика d и толщина полоски h (для рассмотренных случаев равная d) будут наибольшими.

Пусть изменяется только толщина полоски h, принимая значения 1, 10 и 100 мкм (наборы № 1, № 2 и № 3, см. ниже), то есть варьируется константа C₃ при фиксированной C₁. Зададим остальные параметры системы как

(11)

$\begin{gathered} a = 1\,\,{\text{мм}} = {{10}^{{ - 3}}}\,\,{\text{м}},\,\,\,\,d = 100\,\,{\text{мкм}} = {{10}^{{ - 4}}}\,\,{\text{м,}} \\ 0 \leqslant {{С}_{0}} \leqslant 2.5,\,\,\,\,{{C}_{1}} = 2\frac{d}{a} = 0.2,\,\,\,\,0 \leqslant {{С}_{0}} \leqslant 2.5, \\ {{C}_{1}} = 2\frac{d}{a} = 0.2. \\ \end{gathered} $

Соответствующие зависимости построены в логарифмическом масштабе в одной системе координат (см. рис. 3в).

Значения C₀, реализующие максимум, и максимальные размерные значения силы также найдены (наборы значений 1–3).

(12)

Видно, что при увеличении толщины полоски поверхностная плотность силы увеличивается, и, если сравнивать наборы параметров № 1 и № 3, то силы отличаются в 5841 раз. Причем оптимальное значение C₀ увеличивается, хотя и незначительно, для наборов параметров (12).

Теперь пусть изменяется только расстояние до ферромагнетика d, принимая значения 40, 80 и 120 мкм (наборы параметров имеют номера соответственно 4, 5 и 6, см. ниже), то есть с-ейчас варьируется константа C₁ при фиксированной C₃. Зададим остальные параметры системы как

(13)

$\begin{gathered} a = 1\,\,{\text{мм}} = {{10}^{{ - 3}}}\,\,{\text{м}},\,\,\,\,h = 100\,\,{\text{мкм}} = {{10}^{{ - 4}}}\,\,{\text{м,}} \\ 0 \leqslant {{С}_{0}} \leqslant 1,\,\,\,\,{{C}_{3}} = \frac{h}{a} = 0.1. \\ \end{gathered} $

Соответствующие зависимости в логарифмическом масштабе показаны на рис. 3г. Здесь по аналогии с (12) имеем:

(15)

Как видно, с увеличением расстояния до ферромагнетика d сила уменьшается, а оптимальное значение C₀ увеличивается.

В целом вид зависимости для всех рассмотренных случаев не изменяется: рост поверхностной плотности силы наблюдается только до определенного оптимального значения C₀. Экстремум всегда сохраняется.

Таким образом, разработана теория и получена общая аналитическая формула для силы взаимодействия решетки из намагниченных полосок с произвольными параметрами. В рамках данной теории проанализированы закономерности силы взаимодействия магнитной решетки с массивным ферромагнетиком в зависимости от толщины, ширины полоски и расстояния от решетки до ферромагнетика в самом общем случае.

Список литературы

Sander D., Valenzuela S.O., Makarov D. et al. // J. Phys. D. 2017. V. 50. No. 36. Art. No. 363001.
Shimizu Y., Morimoto S., Sanada M., Inoue Y. // IEEJ J. Ind. Appl. 2017. V. 6. No. 6. P. 401.
Huber C., Abert C., Bruckner F. et al. // Appl. Phys. Lett. 2016. V. 109. No. 16. Art. No. 162401.
Luu P.T., Lee J.-Y., Kim J.-W. et al. // J. Eng. Technol. 2018. V. 13. No. 6. P. 2329.
Zhou M., Zhang X., Zhao W. et al. // Chin. J. Electr. Eng. 2019. V. 5. No. 4. P. 40.
Пятаков М.А., Поляков П.А., Русакова Н.Е. // Изв. РАН. Сер. физ. 2020. Т. 84. № 5. С. 719; Piatakov M.A., Polyakov P.A., Rusakova N.E. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 5. P. 593.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1992. 664 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал