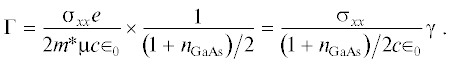Известия РАН. Серия физическая, 2021, T. 85, № 2, стр. 164-169

ВВЕДЕНИЕ

Плазменные возбуждения в двумерных электронных системах (ДЭС) являются достаточно удобными объектами для изучения явлений волновой оптики и эффектов взаимодействия света с веществом.

Для прикладных задач важно понимать механизмы, влияющие на релаксацию плазменных возбуждений. Ширина плазменного резонанса определяется суммой некогерентного столкновительного и излучательного вкладов ${\Delta \omega } = {\gamma } + {\Gamma }$ [1–3], где второе слагаемое описывает когерентное дипольное переизлучение электромагнитных волн колеблющимися двумерными электронами.

В данной работе было проведено детальное исследование излучательного и столкновительного механизмов релаксации циклотронного магнитоплазменного возбуждения. Было показано, что отношение длины волны резонансного микроволнового излучения и латерального размера ДЭС определяет основной механизм релаксации магнитоплазменных возбуждений. В свою очередь это позволяет рассмотреть предельные случаи, где различные механизмы релаксации доминируют по отдельности.

ЭКСПЕРИМЕНТАЛЬНАЯ МЕТОДИКА И ОБРАЗЦЫ

Эксперименты проводились на наборе высококачественных одиночных квантовых ям GaAs/ Al_xGa_1 – xAs. Электронная плотность ${{n}_{s}}$ в разных образцах менялась в диапазоне от 0.02 до 3.0 × 10¹¹ см^–2. Из этих гетероструктур были изготовлены мезы в форме дисков.

Магнитоплазменные моды возбуждались в образце под действием микроволнового излучения в диапазоне частот 1–250 ГГц. Использовались два различных подхода для возбуждения и детектирования микроволновых резонансов в образце.

В первом способе для возбуждения использовалась волноводная методика со свободно распространяющимся по прямоугольному тракту излучением. Образец помещался непосредственно внутрь волновода. При этом использовался оптический метод детектирования микроволнового поглощения [4, 5], основанный на высокой чувствительности спектра рекомбинантной фотолюминесценции ДЭС к разогреву.

Во втором способе использовалась так называемая копланарно-трансмиссионная методика [6, 7]: мезы в форме дисков размещались в щелях копланарного волновода (волновое сопротивление 50 Ом), литографически сформированного на поверхности образца. В такой схеме магнитоплазменные возбуждения возникают под действием поля, сконцентрированного в щелях трансмиссионной линии. Сигнал в диапазоне частот f = 0.1–40 ГГц подводится к линии по коаксиальному кабелю, присоединенному к генератору. Непосредственно измеряемой величиной являлось пропускание копланарного волновода, минимумы пропускания отвечают максимумам микроволнового поглощения в дисках ДЭС.

Эксперименты проводились в гелиевом криостате со сверхпроводящим магнитом при температурах образца T = 1.5–100 К.

ИЗЛУЧАТЕЛЬНАЯ РЕЛАКСАЦИЯ В ДЭС

На рис. 1 изображена магнитодисперсия плазменных возбуждений в дисках ДЭС с диаметром d = 1 мм и электронной концентрацией ${{n}_{s}}~ = 0.9 \cdot {{10}^{{11}}}\,\,{\text{с}}{{{\text{м}}}^{{ - 2}}}.$ При частотах меньше 20 ГГц наблюдается только один пик плазмонного резонанса, смещающийся в сторону больших магнитных полей с увеличением частоты. Этот пик отвечает циклотронной магнитоплазменной моде. Нижняя вставка к рис. 1 показывает, что в больших частотах возникают второй, а после и третий резонансные максимумы, соответствующие кратным гармоникам магнитоплазменного резонанса. При этом с увеличением частоты все моды значительно уширяются, а их частоты асимптотически стремятся к циклотронной частоте. Полученные магнитодисперсии хорошо описываются теоретической зависимостью, выведенной для дипольно-активных магнитоплазменных мод в дисках ДЭС в приближении эллиптического профиля электронной плотности [8, 9]:

где ${{{\omega }}_{p}}$ – плазменная частота в нулевом магнитном поле.

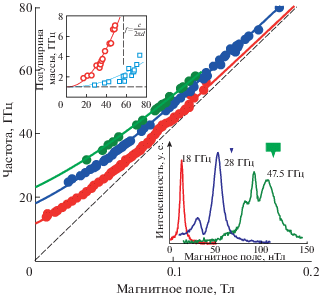
Вставка 2 на рис. 1 демонстрирует зависимость ширины линии от частоты для фундаментальной моды (круги) и ее второй гармоники (квадраты). Экспериментальные значения были получены из полуширины резонансов по магнитному полю ${\Delta }B$ и наклону $\frac{{\partial f}}{{\partial B}}$ магнитодисперсионной зависимости как ${\Delta }f$= $\left( {{{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial B}}} \right. \kern-0em} {\partial B}}} \right){\Delta }B.$ Из рисунка видно, что в низких частотах ширины обеих гармоник стремятся к одному значению ${\Delta }f$ = 1 ГГц, что позволяет сделать вывод, что релаксация в этом случае связана с некогерентным столкновительным рассеянием [10], т.е. ${\Delta \omega } = \frac{1}{\tau }.$ Стремительный рост полуширины линии наблюдается при $f~ \sim {c \mathord{\left/ {\vphantom {c {nd}}} \right. \kern-0em} {nd}}$ (n – эффективный показатель преломления среды). При значениях $f = \frac{c}{{2nd}}$ первая мода пропадает совсем, а вторая продолжает уширение. Этот эффект можно соотнести с появлением второго слагаемого в полуширине линии: ${\Delta \omega } = {\gamma } + {{{\Gamma }}_{{disk}}},$ где ${{{\Gamma }}_{{disk}}}$ отвечает за излучательный вклад когерентно осциллирующих электронов ДЭС. Имеет место оценка [1, 2, 11] ${{{\Gamma }}_{{disk}}} \sim N{{{\Gamma }}_{0}},$ где ${{{\Gamma }}_{0}}$ – величина излучательного затухания одного электрона, а количество осциллирующих на одной частоте электронов в диске можно оценить через длину когерентности ${{L}_{c}}{\text{:}}$ $N \sim {{n}_{s}}L_{c}^{2}.$ Итого:

Под Γ [3] понимается не зависящая от частоты излучательная полуширина линии в бесконечной ДЭС; $n~ = {{\left( {1 + {{n}_{{{\text{GaAs}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + {{n}_{{{\text{GaAs}}}}}} \right)} 2}} \right. \kern-0em} 2}$ – эффективный показатель преломления среды. В данном эксперименте $\Delta f = {{\Gamma } \mathord{\left/ {\vphantom {{\Gamma } {2\pi }}} \right. \kern-0em} {2\pi }}$ = 7 ГГц. Сплошными линиями на вставке к рис. 1 показаны квадратичные аппроксимации полуширины по формуле (2) с параметрами ${{L}_{{c1~}}} = d$ и ${{L}_{{c2}}} = {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ соответственно. Видно, что с увеличением номера моды уменьшается пространственная когерентность. В нашем случае длины отличаются в два раза. При двукратном увеличении диаметра диска в два раза уменьшаются частоты, на которых начинает доминировать излучательный вклад. Отсюда следует, что для дисков основной механизм уширения линии определяется отношением [12] их диаметра к длине волны возбуждающего излучения ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda }.$ При ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda } \ll 1$ преимущественное влияние оказывает некогерентный столкновительный механизм релаксации, а при ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda } \geqslant 1$ – когерентный излучательный.

ТОНКАЯ СТРУКТУРА ЦИКЛОТРОННОГО РЕЗОНАНСА

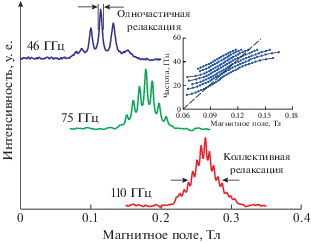
На вставке к рис. 2 представлены магнитодисперсии для образца с концентрацией электронов ${{n}_{s}}$ = 1.6 ⋅ 10¹¹ см^–2 и диаметром мезы d = 2.5 мм. При таких размерах значительными становятся эффекты запаздывания, описывающиеся параметром запаздывания $A~ = \frac{{{{\omega }_{p}}}}{{{{\omega }_{{ph}}}}} \sim 1,$ где плазменная [13] $\left( {{{\omega }_{p}}} \right)$ и фотонная $\left( {{{\omega }_{{ph}}}} \right)$ частоты берутся для одного и того же значения волнового числа, определяемого размером ДЭС. В этом режиме наблюдается сильная гибридизация между плазмонными возбуждениями и фотонными модами в подложке, что приводит к пересечению линии циклотронного резонанса ${{\omega }_{{{\text{ЦР}}}}} = \frac{{eB}}{{m{\text{*}}}}$ (штриховая линия) более пологими магнитодисперсионными кривыми [14–16]. На рисунке продемонстрирована серия линий, соответствующая разным плазменным модам на частотах f < 50 ГГц. В этом диапазоне частот основной вклад в рассеяние вносит некогерентный столкновительный член $\gamma > {{\Gamma }_{{disk}}}.$ Однако ситуация меняется с повышением частоты. В диапазоне до 100 ГГц наблюдается слияние нескольких магнитоплазменных резонансов (рис. 2). Центр огибающей с повышением частоты смещается в область больших магнитных полей и соответствует ${{B}_{{{\text{ЦР}}}}}.$ Это явление можно проинтерпретировать как наблюдение чистого (несмещенного) уширенного $\left( {\Delta \omega = \Gamma } \right)$ циклотронного резонанса, образованного узкими $\left( {\Delta \omega = {1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau }} \right)$ магнитоплазменными возбуждениями. Последние формируют тонкую структуру [17] циклотронного резонанса. Таким образом можно сделать вывод, что циклотронный резонанс не гибридизуется с размерными модами. На частоте f = 110 ГГц отдельные резонансы уже достаточно размыты, что приводит к исчезновению тонкой структуры. Из этого следует два критерия для наблюдения эффекта: 1) когерентный излучательный вклад в рассеяние должен доминировать над одночастичным столкновительным ${{\Gamma }_{{disk~}}} \approx \Gamma > \gamma $ (что эквивалентно ${{{{\sigma }_{{xx}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{xx}}}} {{{\epsilon }_{0}}}}} \right. \kern-0em} {{{\epsilon }_{0}}}} > с$), 2) расстояние между магнитоплазменными резонансами должно быть больше их ширин. Расстояние между частотами N и N + 1 гармоник магнитоплазменного резонанса можно оценить из разложения формулы (2) при условии $\omega \gg {{\omega }_{p}}$ до первого порядка малости и подставляя выражение для плазменной частоты:

где q – волновой вектор плазменной волны в ДЭС. Тогда второе условие ${\Delta \Omega } > {\gamma }$ для наблюдения тонкой структуры соответствует $({{{{\sigma }_{{xy}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{xy}}}} {{{\epsilon }_{0}}}}} \right. \kern-0em} {{{\epsilon }_{0}}}} > c).$

ИССЛЕДОВАНИЕ ВРЕМЕНИ РЕЛАКСАЦИИ ЦИКЛОТРОННОГО РЕЗОНАНСА

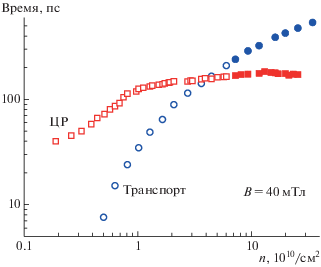
При описании процессов рассеяния в электронных системах во внешнем магнитном поле можно рассмотреть несколько каналов диссипации, и связанных с ними времен. Для случая некогерентной релаксации этими временами будут: полное квантовое, циклотронное и транспортное времена рассеяния. Первое можно оценить через ${{\tau }_{{\text{К}}}} = {{\left[ {\int {{{W}_{{pp{\kern 1pt} '}}}dp{\kern 1pt} '} } \right]}^{{ - 1}}},$ где ${{W}_{{pp{\kern 1pt} '}}}$ – это вероятность рассеяния между состояниями с импульсами p и p'. При этом выражение для транспортного времени выглядит иначе: ${{\tau }_{{\text{Т}}}}$ = ${{\left[ {\int {{{W}_{{pp{\kern 1pt} '}}}\left( {1 - {\text{cos}}\theta } \right)dp{\kern 1pt} '} } \right]}^{{ - 1}}},$ где θ – угол рассеяния. В зависимости от расстояния действия рассеивающего потенциала возможны различные соотношения между транспортным и полным квантовым временами [18]. Для короткодействующего потенциала ${{{{\tau }_{{\text{К}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{К}}}}} {{{\tau }_{{\text{Т}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{Т}}}}}} \approx 1$ (электрон-фононное рассеяние) и ${{{{\tau }_{{\text{К}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{К}}}}} {{{\tau }_{{\text{Т}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{Т}}}}}} \ll 1$ для дальнодействующего (потенциал донора). До сих пор во многих работах при оценке циклотронного времени рассеяния полагают ${{\tau }_{{{\text{ЦР}}}}} = {{\tau }_{{\text{К}}}}.$ Это равенство не является до конца верным, что и будет продемонстрировано далее. В этой части работы исследуется именно соотношение между циклотронным и транспортным временем рассеяния.

Для исследования времени релаксации циклотронного резонанса изучалось микроволновое поглощение ДЭС в дисках диаметром d = 1 мм в частотном диапазоне до 40 ГГц. В таком режиме ширина линии определяется в основном циклотронным временем релаксации $\Delta \omega = {1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{{\text{ЦР}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{ЦР}}}}}}}$ (радиационным уширением в данном случае можно пренебречь, так как для используемого образца ${\Gamma \mathord{\left/ {\vphantom {\Gamma {2\pi }}} \right. \kern-0em} {2\pi }}$ ≈ 0.3 ГГц, что сильно меньше чем минимальная резонансная полуширина $\Delta f$ = 4 ГГц). Для измерения зависимости ширины линии от температуры была выбрана частота возбуждающего сигнала f = 37 ГГц. Экспериментальные значения были получены из полуширины резонансов по магнитному полю $\Delta B$ и наклону $\frac{{\partial f}}{{\partial B}}$ магнитодисперсионной зависимости. На рис. 3 изображена температурная зависимость времени релаксации для циклотронного резонанса (красные круги). Синими кругами показана температурная зависимость транспортного времени релаксации, вычисленного по формуле:

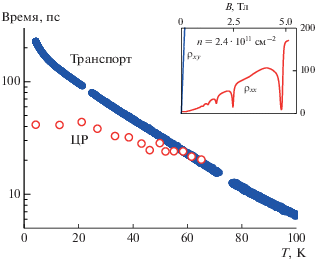
где ${{\rho }_{{xx}}}$ – диагональная компонента тензора удельного сопротивления в нулевом магнитном поле. Транспортные измерения проводились в геометрии холловского мостика. Видно, что с ростом температуры время транспортной релаксации уменьшается и сравнивается с циклотронным. Этот случай хорошо описывается в приближении ${{\tau }_{{{\text{ЦР}}}}} = {{\tau }_{{\text{К}}}}{\text{:}}$ при низких температурах электронное рассеяние в основном определяется дальнодействующим потенциалом донора (${{{{\tau }_{{\text{К}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{К}}}}} {{{\tau }_{{\text{Т}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{Т}}}}}} \ll 1$), в то время как при повышении температур основной вклад вносит электрон-фононное рассеяние (${{{{\tau }_{{\text{К}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{К}}}}} {{{\tau }_{{\text{Т}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{Т}}}}}} \approx 1$). Значимость последнего эффекта подтверждается вычислением квантового времени рассеяния $\left( {{{\tau }_{{\text{К}}}} \approx 1} \right)$ из осцилляций Шубникова–де Газа (вставка на рис. 3).

Для изучения зависимости времени релаксации от электронной концентрации в ДЭС была использована оптическая методика детектирования микроволнового поглощения. На рис. 4 представлена зависимость циклотронного и транспортного времен релаксации от электронной концентрации в диапазоне 2 · 10⁹–3 · 10¹¹ см^–2. Видно, что с ростом концентрации время транспортной релаксации увеличивается вдвое, в то время как циклотронное меняется мало. При ${{n}_{s}}$ > > 4 · 10¹⁰ см^–2 оно фиксируется вблизи значения ${{\tau }_{{\text{К}}}} \approx 150~$ пс. Оказалось, что в области низких концентраций (${{n}_{s}}$ < 4 · 10¹⁰ см^–2) ${{{{\tau }_{{{\text{ЦР}}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{{\text{ЦР}}}}}} {{{\tau }_{{\text{Т}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{Т}}}}}} > 1.$ Это обстоятельство нельзя объяснить в рамках приближения ${{\tau }_{{{\text{ЦР}}}}} \simeq {{\tau }_{{\text{К}}}},$ поскольку неэффективность малоуглового рассеяния электронов всегда приводит к ${{{{\tau }_{{\text{К}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{\text{К}}}}} {{{\tau }_{{\text{Т}}}}}}} \right. \kern-0em} {{{\tau }_{{\text{Т}}}}}} < 1.$ Возможно, что подобное поведение связано с локализацией носителей заряда, что приводит к различию в механизмах диссипации у разных групп. Приведенные методы измерений позволяют получить среднее время, куда взвешенно входят вклады разных типов релаксаций. Транспортная методика измеряет время релаксации только для делокализованных состояний с характерным пространственным расстоянием, сравнимым с размером образца (миллиметры). При этом циклотронное время релаксации определяется электронным рассеянием на характерных расстояниях сравнимых с радиусом циклотронной орбиты.

ЗАКЛЮЧЕНИЕ

В данной работе были исследованы релаксации плазменных возбуждений в ДЭС. Показано, что вклад каждого из механизмов в ширину линии циклотронного магнитоплазменного резонанса определяется отношением ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda }$ длины волны возбуждающего излучения к размеру образца. Так в случае ${d \mathord{\left/ {\vphantom {d \lambda }} \right. \kern-0em} \lambda } \ll 1$ преобладающим оказывается некогерентное столкновительное уширение, а при $\frac{d}{\lambda } \geqslant 1~$ – когерентное излучательное. Помимо этого установлено, что по своей природе циклотронный резонанс является чистым резонансом и не гибридизуется с размерными магнитоплазменными модами. При этом если когерентный излучательный вклад в рассеяние доминирует над одночастичным столкновительным, и выполнено условие $({{{{\sigma }_{{xy}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{xy}}}} {{{\epsilon }_{0}}}}} \right. \kern-0em} {{{\epsilon }_{0}}}} > c),$ то наблюдается тонкая структура циклотронного резонанса: наложение на контур ЦР узких магнитоплазменными мод.

Для случая столкновительной релаксации произведен сравнительный анализ циклотронного и транспортного времен рассеяния. Экспериментально показано, что с повышением температуры транспортное время стремится к циклотронному, а при $T > 60$ К они совпадают. Малая зависимость времени релаксации от электронной концентрации отличает циклотронное время от транспортного и не описывается в рамках существующих теорий.

Работа выполнена в рамках темы государственного задания ИФТТ РАН.