Известия РАН. Серия физическая, 2021, T. 85, № 4, стр. 486-489
Нелинейная модель Монте-Карло ускорения частиц бесстолкновительной ударной волной при различных законах рассеяния частиц
С. М. Осипов 1, *, А. М. Быков 1, 2
1 Федеральное государственное бюджетное учреждение науки
Физико-технический институт имени А.Ф. Иоффе Российской академии наук
Санкт-Петербург, Россия
2 Федеральное государственное автономное образовательное учреждение высшего образования
Санкт-Петербургский политехнический университет Петра Великого
Санкт-Петербург, Россия
* E-mail: osm2004@mail.ru
Поступила в редакцию 19.10.2020
После доработки 19.11.2020
Принята к публикации 28.12.2020
Аннотация
Представлена нелинейная модель Монте-Карло, в которой спектры ускоренных частиц и магнитных флуктуаций рассчитаны самосогласованно, с учетом нелинейных эффектов и развития плазменных неустойчивостей в окрестности сильной ударной волны. Рассмотрены различные модельные режимы рассеяния частиц. Показано, что спектр ускоренных частиц значительно смягчается в случае использования обобщенного режима мелкомасштабного рассеяния, по сравнению с бомовским законом рассеяния.
ВВЕДЕНИЕ
Бесстолкновительные ударные волны (УВ) в остатках сверхновых звезд являются наиболее вероятными ускорителями галактических космических лучей (КЛ) до энергий порядка 100 ТэВ [1‒5], и могут вносить вклад [6] в наблюдаемые спектры КЛ с энергиями выше ПэВ [7]. Вблизи фронтов бесстолкновительных УВ в остатках сверхновых звезд происходит ускорение частиц по механизму Ферми первого порядка при их рассеянии на флуктуациях магнитного поля. Магнитные поля в предфронте УВ усиливаются за счет плазменных неустойчивостей, вызванных анизотропией функции распределения ускоренных частиц. Значительная часть потока энергии, натекающего на фронт УВ, идет на ускорение частиц. Градиент давления ускоренных частиц модифицирует течение плазмы в предфронте ударной волны. В процессе развития неустойчивостей, рассеивающие центры начинают двигаться относительно системы покоя фоновой плазмы. Значение скорости относительного движения рассеивающих центров и системы покоя фоновой плазмы значительно влияет на процесс ускорения частиц и, соответственно, на усиление магнитных флуктуаций. В работе [8] развита нелинейная модель диффузионного ускорения частиц УВ, позволяющая рассчитывать спектры ускоренных частиц и флуктуаций магнитных полей, усиленных нерезонансными токовыми неустойчивостями. Модель включает в себя каскад турбулентной энергии флуктуаций и нагрев фоновой плазмы при диссипации мод. В данной работе рассматривается зависимость формы спектра КЛ от модели рассеяния, определяющей длины свободного пробега частиц.
ОПИСАНИЕ МОДЕЛИ
В одномерной модели Монте-Карло [8] частицы разделены на фоновые и ускоренные. Ускоренной считается частица, хотя бы раз пересекшая поверхность УВ назад в предфронт. Распределение фоновых частиц далеко в невозмущенном предфронте характеризуется температурой и концентрацией, однако в окрестности вязкого скачка описание фоновой плазмы ведется на уровне отдельных частиц. Это позволяет без введения дополнительного параметра модели описать инжекцию частиц в процесс ускорения. Описание ускоренных частиц ведется на уровне индивидуальных частиц. Распространение частиц описывается длиной свободного пробега, определяемой спектром турбулентной энергии W(x, k), и величиной импульса частицы в локальной системе покоя рассеивающих центров. Предполагается, что система покоя рассеивающих центров движется относительно системы покоя фоновой плазмы со υscat [8, 9]. В этой локальной системе отсчета рассеяние КЛ предполагается упругим и изотропным. В данной стационарной одномерной модели структура течения плазмы в предфронте УВ, а также спектры магнитных флуктуаций и КЛ определяются на основе итерационной процедуры. Подбирается профиль скорости течения фоновой плазмы u(x) таким образом, чтобы достигалось выполнение закона сохранения потока импульса в предфронте УВ. Закон сохранения массы в модели достигается автоматически. Закон сохранения потока энергии будет выполнен при достижении выполнения закона сохранения потока импульса [8, 9], если в предфронте УВ
(1)
${{\upsilon }_{{scat}}}\left( x \right) = - {{\int\limits_{\left( k \right)} {\Gamma \left( {x,k} \right)W(x,k)} dk} \mathord{\left/ {\vphantom {{\int\limits_{\left( k \right)} {\Gamma \left( {x,k} \right)W(x,k)} dk} {\frac{{d{{P}_{{cr}}}\left( x \right)}}{{dx}}}}} \right. \kern-0em} {\frac{{d{{P}_{{cr}}}\left( x \right)}}{{dx}}}},$В рассматриваемой модели вязкий скачок УВ покоится в точке x = 0. Граница свободного ухода КЛ находится в точке x = LFEB. Ускоренные частицы, пересекшие x = LFEB, уходят из системы и уносят поток энергии Qesc. В данной работе LFEB = = –3 ∙ 108rg0, где ${{r}_{{g0}}} = \frac{{{{u}_{{sh}}}{{m}_{p}}c}}{{e{{B}_{0}}}},$ B0 = 3 мкГс значение постоянного магнитного поля в далеком предфронте, mp – масса протона, с – скорость света, e – элементарный заряд, ush = 5000 км ⋅ с–1 – скорость ударной волны. Концентрация фоновой плазмы в далеком предфронте n0 = 0.3 см–3. Потоки плазмы за границей свободного ухода считаются невозмущенными и обозначаются в дальнейшем подстрочным индексом 0. Величины непосредственно перед фронтом ударной волны имеют подстрочный индекс 1, а за фронтом ударной волны они имеют подстрочный индекс 2. За фронтом ударной волны течение однородно, а υscat = 0. Распространение частиц на каждой итерации происходит при фиксированных значениях скорости системы рассеивателей и спектре флуктуаций. Далее, из полученной функции распределения частиц, находятся ее моменты, скорость фоновой плазмы u(x), показатели роста турбулентности для всех волновых чисел, поток энергии Qesc. (который из законов сохранения определяет полное сжатие плазмы ударной волной Rtot). Скорость υscat находим из выражения (1). Затем процесс повторяется до тех пор, пока закон сохранения потока импульса не выполнится с заданной точностью. Детали итерационной процедуры описаны в работах [8, 9].
В модели Монте-Карло частицы движутся прямолинейно и равномерно на расстояниях меньших длины свободного пробега, а затем происходит рассеяние, то есть изменение направления импульса частицы без изменения модуля ее импульса в системе покоя рассеивающих центров.
РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Рассматривается плазма, состоящая из протонов и электронов. В расчетах используется модель турбулентного каскада А.Н. Колмогорова [10], включенная в уравнение изменения W(x, k) вблизи УВ [11], включающего также диссипацию мод и адиабатическое изменение спектра. Cпектр турбулентной энергии W0(k) ~ k–5/3 в далеком предфронте. Мы в данной работе моделируем самосогласованную задачу ускорения частиц в двух случаях, отличающихся выражением для длины пробега КЛ в предфронте УВ, при всех остальных одинаковых параметрах модели. При решении задачи об ускорении частиц астрофизическими УВ часто используют бомовскую модель длины пробега
где p – импульс частицы. Однако, для продольной длинны пробега более адекватным феноменологическим выражением можно считать длину пробега в обобщенном режиме мелкомасштабных рассеивателей, соответствующую моделированию пробегов частиц в турбулентной среде [12],(5)
${{\lambda }_{{ss}}}\left( {x,p} \right) = {{\left( {\frac{{pc}}{{\pi e}}} \right)}^{2}}{{\left[ {\int\limits_{{{k}_{{res}}}}^\infty {\frac{{W(x,k{\kern 1pt} ')}}{{k{\kern 1pt} '}}dk{\kern 1pt} '} } \right]}^{{ - 1}}},$а связь импульса с резонансным волновым числом определяется соотношением
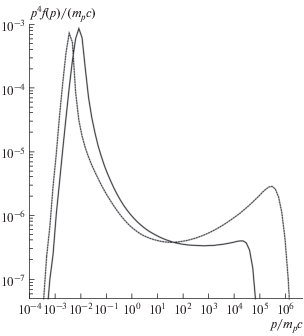
Как видно из рис. 1 модуль скорость рассеивающих центров в случае обобщенного режима мелкомасштабных рассеивателей (5) значительно больше, чем в случае бомовской диффузии (4), и не спадает вплоть до фронта УВ. Также полное сжатие УВ в случае обобщенного режима мелкомасштабных рассеивателей Rtot ≈ 5.06, а в бомовском случае Rtot ≈ 10.4. При этом значение магнитного поля за фронтом УВ в случае обобщенного режима мелкомасштабных рассеивателей Beff, 2 ≈ ≈ 371 мкГс не на много меньше, чем в бомовском случае Beff, 2 ≈ 465 мкГс. Как видно из рис. 2 спектр частиц на высоких энергиях в случае обобщенного режима мелкомасштабных рассеивателей стал значительно мягче, а максимальный импульс ускоренных частиц меньше, чем в бомовской модели рассеяния.
Рис. 1
Зависимости скорости фоновой плазмы u(x) (тонкие кривые) и модуля скорости движения рассеивающих центров относительно системы покоя фоновой плазмы |υscat(x)| (кривые полужирными линиями) от координаты x в предфронте УВ. Расчет для обобщенного режима мелкомасштабных рассеивателей – сплошные кривые, расчет для бомовской диффузии – штриховые кривые.
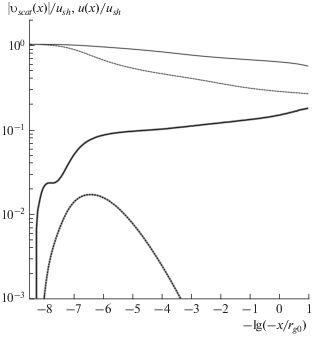
Рис. 2.
Спектр протонов на фронте УВ. Расчет для обобщенного режима мелкомасштабных рассеивателей – сплошные кривые, расчет для бомовской диффузии – штриховые кривые.
Результаты работы были получены с использованием вычислительных ресурсов суперкомпьютерного центра Санкт-Петербургского политехнического университета Петра Великого (scc.spbstu.ru).
Список литературы
Amato E. // Int. J. Mod. Phys. D. 2014. V. 23. No. 7. Art. No. 14300.
Bell A.R. // Astropart. Phys. 2013. V. 43. P. 56.
Malkov M.A., Aharonian F.A. // Astrophys. J. 2019. V. 881 Art. No. 2.
Ptuskin V., Zirakashvili V., Seo E.-S. // Astrophys. J. 2013. V. 763. Art. No. 47.
Sveshnikova L.G., Strelnikova O.N., Ptuskin V.S. // Astropart. Phys. 2013. V. 50. P. 33.
Bykov A.M., Ellison D.C., Marcowith A., Osipov S.M. // Space Sci. Rev. 2018. V. 214. Art. No. 41.
Budnev N.M., Chiavassa A., Gress O.A. et al. // Astropart Phys. 2020. V. 117. Art. No. 102406.
Bykov A.M., Ellison D.C., Osipov S.M., Vladimirov A.E. // Astrophys. J. 2014. V. 789. Art. No. 137.
Osipov S.M., Bykov A.M., Ellison D.C. // J. Phys. Conf. Ser. 2019. V. 1400. Art. No. 022004.
Matthaeus W.H., Oughton S., Zhou Y. // Phys. Rev. E. 2009. V. 79. Art. No. 035401.
Bykov A.M., Ellison D.C., Osipov S.M. // Phys. Rev. E. 2017. V. 95. Art. No. 033207.
Casse F., Lemoine M., Pelletier G. // Phys. Rev. D. 2002. V. 65. Art. No. 023002.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


