Известия РАН. Серия физическая, 2021, T. 85, № 5, стр. 638-644
Применение эффективных нуклон-нуклонных сил, полученных в рамках теории релятивистского среднего поля, к динамическому моделированию слияния тяжелых ионов
М. В. Чушнякова 1, И. И. Гончар 2, Н. А. Хмырова 2, А. А. Климочкина 3, *
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Омский государственный технический университет”
Омск, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Омский государственный университет путей сообщения”
Омск, Россия
3 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”
Москва, Россия
* E-mail: klimann16@gmail.com
Поступила в редакцию 20.11.2020
После доработки 28.12.2020
Принята к публикации 27.01.2021
Аннотация
Высокоточные экспериментальные сечения слияния сферических ядер проанализированы количественно с использованием эффективного взаимодействия, полученного в рамках теории релятивистского среднего поля. Из четырех рассмотренных наборов параметров только в двух случаях имеется кулоновский барьер. Сечения слияния, вычисленные с одним из этих наборов, хорошо согласуются с экспериментальными данными.
ВВЕДЕНИЕ
Известно, что теория релятивистского среднего поля (ТРСП) успешно описывает такие статические свойства ядер как энергии связи и кулоновские форм-факторы [1–3]. В то же время имеется множество высокоточных данных (с типичной погрешностью порядка 1%) по слиянию (захвату) сложных ядер [4, 5]. Эти данные детально анализировались с помощью модели двойной свертки с эффективными нуклон-нуклонными (NN) силами M3Y [6, 7]. Поэтому представляется логичным попытаться описать те же данные, используя эффективные силы, полученные в рамках теории релятивистского среднего поля.
Это эффективное взаимодействие имеет вид [8]
(1)
$\begin{gathered} {{\nu }_{{NN}}}\left( r \right) = \frac{{g_{{{\omega }}}^{2}}}{{4\pi }}~\frac{{\exp \left( {{{ - {{m}_{{{\omega }}}}rc} \mathord{\left/ {\vphantom {{ - {{m}_{{{\omega }}}}rc} \hbar }} \right. \kern-0em} \hbar }} \right)}}{r} + \frac{{g_{{{\rho }}}^{2}}}{{4\pi }}~\frac{{\exp \left( {{{ - {{m}_{{{\rho }}}}rc} \mathord{\left/ {\vphantom {{ - {{m}_{{{\rho }}}}rc} \hbar }} \right. \kern-0em} \hbar }} \right)}}{r} - \\ - \,\,\frac{{g_{{{\sigma }}}^{2}}}{{4\pi }}~\frac{{\exp \left( {{{ - {{m}_{{{\sigma }}}}rc} \mathord{\left/ {\vphantom {{ - {{m}_{{{\sigma }}}}rc} \hbar }} \right. \kern-0em} \hbar }} \right)}}{r} + \frac{{g_{2}^{2}}}{{4\pi }}r\exp \left( {{{ - 2{{m}_{\sigma }}rc} \mathord{\left/ {\vphantom {{ - 2{{m}_{\sigma }}rc} \hbar }} \right. \kern-0em} \hbar }} \right) + \\ + \,\,\frac{{g_{3}^{2}}}{{4\pi }}~\frac{{\exp \left( {{{ - 3{{m}_{{{\sigma }}}}rc} \mathord{\left/ {\vphantom {{ - 3{{m}_{{{\sigma }}}}rc} \hbar }} \right. \kern-0em} \hbar }} \right)}}{r} - {{J}_{{00}}}\delta \left( {\vec {r}} \right). \\ \end{gathered} $Массы мезонов ${{m}_{{{\omega }}}},$ ${{m}_{{{\rho }}}},$ ${{m}_{{{\sigma }}}}$ и константы связи мезонов с нуклонами ${{g}_{{{\omega }}}},$ ${{g}_{{{\rho }}}},$ ${{g}_{{{\sigma }}}},$ ${{g}_{2}},$ ${{g}_{3}},$ полученные из подгонки статических свойств ядер, представлены в табл. 1 с соответствующими ссылками.
Таблица 1.
Массы мезонов и соответствующие константы связи, полученные из подгонки статических свойств ядер, с соответствующими ссылками
| NL1 [1, 2] | NL2 [2] | NL3 [8, 9] | HS [10–12] | |
|---|---|---|---|---|
| ${{m}_{\omega }}{{c}^{2}}$/МэВ | 795.359 | 780.0 | 782.501 | 783 |
| ${{m}_{\rho }}{{c}^{2}}$/МэВ | 763.0 | 763.0 | 763.000 | 770 |
| ${{m}_{\sigma }}{{c}^{2}}$/МэВ | 492.25 | 504.89 | 508.194 | 520 |
| ${{{{g}_{\omega }}} \mathord{\left/ {\vphantom {{{{g}_{\omega }}} {\sqrt {\hbar c} }}} \right. \kern-0em} {\sqrt {\hbar c} }}$ | 13.285 | 11.493 | 12.868 | 13.8 |
| ${{{{g}_{\rho }}} \mathord{\left/ {\vphantom {{{{g}_{\rho }}} {\sqrt {\hbar c} }}} \right. \kern-0em} {\sqrt {\hbar c} }}$ | 4.975 | 5.507 | 4.474 | 8.08 |
| ${{{{g}_{\sigma }}} \mathord{\left/ {\vphantom {{{{g}_{\sigma }}} {\sqrt {\hbar c} }}} \right. \kern-0em} {\sqrt {\hbar c} }}$ | 10.138 | 9.111 | 10.271 | 10.47 |
| ${{{{g}_{2}}} \mathord{\left/ {\vphantom {{{{g}_{2}}} {\left( {{\text{фм\;}}\sqrt {\hbar c} } \right)}}} \right. \kern-0em} {\left( {{\text{фм\;}}\sqrt {\hbar c} } \right)}}$ | –12.172 | -2.304 | –10.431 | 0 |
| ${{{{g}_{3}}} \mathord{\left/ {\vphantom {{{{g}_{3}}} {\sqrt {\hbar c} }}} \right. \kern-0em} {\sqrt {\hbar c} }}$ | –36.265 | 13.783 | –28.885 | 0 |
Структура эффективных сил, полученных на основе ТРСП, подобна структуре хорошо известного M3Y взаимодействия. Последнее имеет вид:
(2)
${{\nu }_{{NN}}}\left( r \right) = {{G}_{1}}\frac{{\exp \left( {{{ - r} \mathord{\left/ {\vphantom {{ - r} {{{r}_{1}}}}} \right. \kern-0em} {{{r}_{1}}}}} \right)}}{{{r \mathord{\left/ {\vphantom {r {{{r}_{1}}}}} \right. \kern-0em} {{{r}_{1}}}}}} - {{G}_{2}}~\frac{{\exp \left( {{{ - r} \mathord{\left/ {\vphantom {{ - r} {{{r}_{2}}}}} \right. \kern-0em} {{{r}_{2}}}}} \right)}}{{{r \mathord{\left/ {\vphantom {r {{{r}_{2}}}}} \right. \kern-0em} {{{r}_{2}}}}}} - {{J}_{{00}}}{{\delta }}\left( {\vec {r}} \right).$В работе [13] приводятся следующие значения для параметров формулы (2): ${{G}_{1}}$ = 11062 МэВ, ${{G}_{2}}$ = = 2537.5 МэВ, ${{r}_{1}}$ = 0.25 фм, ${{r}_{2}}$ = 0.40 фм, ${{J}_{{00}}}$ = = 592 МэВ ⋅ фм3 (парижское взаимодействие). Мы используем это же значение ${{J}_{{00}}}$ и для ТРСП взаимодействия. Отметим, что энергетическая зависимость этого взаимодействия не учитывается, так как она несущественна в данной задаче. Прямые части M3Y и ТРСП взаимодействий, т.е. ${{\nu }_{{NN}}}$ без слагаемых с дельта-функцией, сравниваются между собой на рис. 1. Они помечены индексом “0”: M3Y_0 и т.д. Все пять профилей ${{\nu }_{{NN}}}\left( r \right)$ похожи друг на друга, что заставляет ожидать похожих ядро-ядерных сил, полученных с использованием этих нуклон-нуклонных взаимодействий.
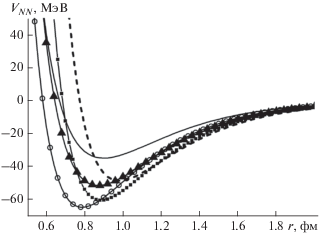
Рис. 1.
Прямая часть эффективного нуклон-нуклонного взаимодействия (т.е. без учета члена с дельта-функцией). Использованы следующие NN силы: сплошная линия без символов – M3Y_0, штриховая линия – NL1_0, сплошная линия с открытыми кружками – NL2_0, сплошная линия с черными квадратами – NL3_0, сплошная линия с черными треугольниками – HS_0.
ЭНЕРГИЯ ЯДРО-ЯДЕРНОГО ВЗАИМОДЕЙСТВИЯ
В настоящей работе энергия сильного ядерного взаимодействия (СиЯВ, ${{U}_{n}}$) вычисляется методом двойной свертки:
(3)
${{U}_{n}}\left( R \right) = \int {d{{{\vec {r}}}_{P}}} \int {d{{{\vec {r}}}_{T}}{{{{\rho }}}_{P}}\left( {{{{\vec {r}}}_{P}}} \right)} {{\nu }_{{NN}}}\left( {\left| {\vec {R} + {{{\vec {r}}}_{T}} - {{{\vec {r}}}_{P}}} \right|} \right){{{{\rho }}}_{T}}\left( {{{{\vec {r}}}_{T}}} \right).$Здесь $\vec {R}$ – вектор, соединяющий центры масс сталкивающихся ядер; ${{\vec {r}}_{P}}$ и ${{\vec {r}}_{T}}$ – радиус-векторы двух взаимодействующих точек снаряда и мишени соответственно. Рисунки, иллюстрирующие этот процесс, можно найти во многих публикациях (см., например, [14, 15]). Энергия кулоновского взаимодействия вычисляется посредством двойной свертки по формуле, аналогичной формуле (3). Нуклонные и зарядовые плотности, необходимые для этих вычислений, взяты из работы [7]. Они были получены методом Хартри–Фока с силами Скирма, как описано в работе [16]. При этом учитывался тензорный характер сил и использовалась SKX параметризация [17] (далее мы ссылаемся на них как на SKX HF плотности).
Вычисленные таким образом потенциалы СиЯВ и полные потенциалы взаимодействия (т.е. с учетом кулоновской составляющей) показаны на рис. 2 для реакции 12C + 92Zr при нулевом угловом моменте. Вычисления, результаты которых показаны на рис. 2а и 2б, проведены без учета слагаемого с дельта-функцией. Потенциалы СиЯВ на рис. 2а не убывают при уменьшении $R$ и, соответственно, потенциалы ${{U}_{{tot}}}\left( R \right)$ на рис. 2б не имеют барьеров. Стало быть, их нельзя использовать для описания данных по слиянию (захвату) при столкновении тяжелых ионов. Однако потенциалы ${{U}_{n}}$ на рис. 2а возрастают с разной скоростью: те из них, что соответствуют наборам параметров NL2_0 и HS_0 возрастают с убыванием $R$ значительно медленнее, чем два других ТРСП-потенциала, NL1_0 и NL3_0. Для сравнения на рис. 2 показаны также потенциалы, полученные с силами M3Y.
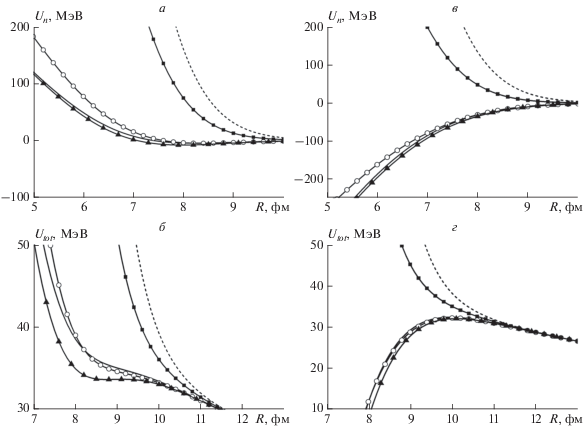
Рис. 2.
СиЯВ ((a) и (в)) и полный ядро-ядерный потенциал ((б) и (г)) в зависимости от межцентрового расстояния для реакции 12C + 92Zr. Панели (а) и (б) соответствуют расчетам без обменного слагаемого, панели (в) и (г) – расчетам с учетом этого слагаемого. Все обозначения как на рис. 1.
В качестве следующего шага мы вычислили ТРСП ${{U}_{n}}$ потенциалы с учетом ${{J}_{{00}}}$ (т.е. с обменным слагаемым). Результаты этих расчетов снабжены индексом “Е”. Результирующие потенциалы показаны на рис. 2в и 2г. Для параметров NL1 и NL3 учет обменного слагаемого качественно не изменил картину: полные потенциалы взаимодействия по-прежнему не имеют барьеров. Однако, потенциал ${{U}_{n}}$(NL2_E) убывает подобно ${{U}_{n}}$(M3Y_E) (рис. 2в) и в результате на рис. 2г появляется барьер. Форма и высота этого барьера близки к полученным с M3Y_E нуклон-нуклонным взаимодействием. Силы HS из работы [11] также приводят к ядро-ядерному потенциалу, который убывает по мере сближения ядер (см. рис. 2в). Соответственно, полный потенциал ${{U}_{{tot}}}$ (HS_E) имеет барьер, который очень похож на барьер ${{U}_{{tot}}}$ (NL2_E) (см. рис. 2г). Поэтому мы проводим сравнение с экспериментальными данными, используя только потенциал ${{U}_{{tot}}}$ (HS_E).
Попытаемся качественно понять поведение ТРСП потенциалов СиЯВ, анализируя нуклон-нуклонные силы на рис. 1. Сравнивая кривые, соответствующие ТРСП и M3Y, можно было бы ожидать, что все ТРСП СиЯВ потенциалы будут убывать при сближении ядер, приводя к появлению барьера на графике ${{U}_{{tot}}}\left( R \right).$ В самом деле, силы ${{\nu }_{{NN}}}$(ТРСП) выглядят очень похожими на ${{\nu }_{{NN}}}$(M3Y), причем минимумы у ${{\nu }_{{NN}}}$(ТРСП) даже глубже.
Чтобы разобраться в этом кажущемся противоречии, мы показываем на рис. 3 прямые части всех пяти νNN-потенциалов при малых значениях аргумента. В таком представлении видно, что ${{\nu }_{{NN}}}$(NL1_0) и ${{\nu }_{{NN}}}$(NL3_0) при уменьшении $r$ возрастают гораздо быстрее, чем три остальных. Более того, $r$-зависимости νNN(NL2_0) и νNN(HS_0) при малых значениях $r$ становятся близки к ${{\nu }_{{NN}}}$(M3Y_0). Таким образом, естественно ожидать, что при использовании этих трех нуклон-нуклонных сил барьеры будут получаться близкими по высоте и радиусу.
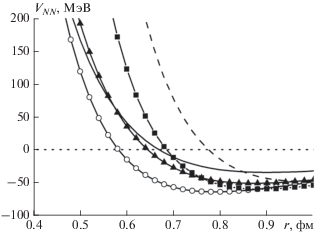
Рис. 3.
Прямая часть эффективного нуклон-нуклонного взаимодействия (т.е. без учета члена с дельта-функцией): детальная картина для малых расстояний между нуклонами. Все обозначения как на рис. 1.
В потенциалах ${{\nu }_{{NN}}}$(NL1_0) и ${{\nu }_{{NN}}}$(NL3_0) отталкивание наступает при слишком большом расстоянии между нуклонами по сравнению c тремя потенциалами, обсуждавшимися в предыдущем абзаце. Данное наблюдение, как нам представляется, объясняет отсутствие барьеров для этих двух потенциалов.
Энергия СиЯВ вычислялась в рамках ТРСП ранее в работах [11, 12, 18]. NN-силы из работы [11] (HS_0) показаны на рис. 1 и рис. 3, а барьеры, которые получаются при использовании HS_E представлены ниже в табл. 2. Наши вычисления приблизительно воспроизводят барьер для реакции 14C + 208Pb (см. рис. 2 в [11]). Мы вычисляли барьер для реакции 12C + 208Pb и получили ${{U}_{{B0}}}$(NL2_E) = 58.3 МэВ и ${{U}_{{B0}}}$(HS_E) = 58.0 МэВ. Эти значения близки к ${{U}_{{B0}}} \approx 57$ МэВ (см. вставку на рис. 2 в [11]).
Таблица 2.
Реакции, результаты расчетов для которых представлены на рис. 4; оптимальные значения амплитуды коэффициента трения ${{K}_{{Rm}}};$ соответствующие значения $\chi _{m}^{2}.$ В последних колонках приведены высоты кулоновских барьеров для нулевого углового момента ${{U}_{{B0}}},$ вычисленные в настоящей работе с HS_E-параметрами и в работе [7] с M3Y_E-параметрами
| Реакция | ${{K}_{{Rm}}}$ (зс · ГэВ–1) | $\chi _{m}^{2}$ | ${{U}_{{B0}}}$ (МэВ) | |||
|---|---|---|---|---|---|---|
| данная работа, HS_E |
работа [7], M3Y_E |
данная работа, HS_E |
работа [7], M3Y_E |
данная работа, HS_E |
работа [7], M3Y_E |
|
| 16O + 92Zr | 17 | 27 | 7 | 17 | 41.90 | 41.6 |
| 16O + 144Sm | 10 | 16 | 7 | 8 | 61.05 | 60.7 |
| 12C + 208Pb | 9 | 16 | 7 | 7 | 57.95 | 57.8 |
| 28Si + 92Zr | 12 | 19 | 3 | 3 | 71.01 | 70.5 |
| 12C + 144Sm | 17 | 23 | 0.07 | 0.04 | 46.64 | 46.4 |
Сравнение наших результатов с результатами работы [18] вызывает трудности, так как подходы, использованные в этих двух работах, слишком различны. В самом деле, мы используем SKX HF плотности, тогда как в работе [18] использованы плотности, полученные в релятивистском подходе Хартри–Боголюбова. Кроме того, в [18] для NN сил использовано приближение дельта-функции, тогда как мы используем ТРСП-силы с конечными радиусами взаимодействия.
Наш результат в отношении отсутствия барьера при использовании NL3-сил как будто находится в противоречии с результатами работы [12], в которой сечения слияния вычислялись с использованием этого NN взаимодействия. Один источник кажущегося противоречия – различные плотности, использованные в [12] и в настоящей работе. А именно, в [12] плотности получались с использованием того же NL3 взаимодействия, тогда как у нас используются SKX HF плотности. Другая возможная причина состоит в том, что в сравниваемых двух работах расчеты сделаны для разных реакций. Следует заметить, что в работе [8] для реакции p + 120Te полный потенциал взаимодействия, основанный на NL3 NN силах, не имеет барьера как и в наших расчетах. Вопрос об этом кажущемся противоречии, возможно, требует дальнейшего изучения.
ВЫЧИСЛЕНИЕ СЕЧЕНИЙ СЛИЯНИЯ
Перейдем теперь к сравнению с экспериментом. Для этой цели мы выбрали высокоточные данные по надбарьерным сечениям слияния в реакциях 16O + 92Zr и 28Si + 92Zr [19], 16O + 144Sm [20], 16O + 208Pb [21], 12C + 144Sm [22] (данные зачастую взяты из базы данных [23]). Следует заметить, что экспериментальные погрешности в работах [19–21] составляют 0.5–1%, тогда как в [22] – около 5%.
Сечения слияния в данной работе вычисляются с помощью флуктуационно-диссипативной траекторной модели, разработанной в [6, 7, 24]. Эта модель подробно описана и тщательно протестирована в указанных работах, поэтому здесь приведено лишь ее краткое описание.
Физическая картина модели похожа на использованную в работе [25]: воображаемая броуновская частица с приведенной массой движется под действием консервативной, диссипативной и случайной сил. Мы изучаем процесс при энергиях столкновения заметно выше кулоновского барьера, так что квантовые эффекты (туннелирование и связь каналов) не учитываются. В рассматриваемых реакциях участвуют только сферические ядра. Эти ядра довольно жесткие, благодаря по крайней мере одной (нейтронной или протонной) замкнутой оболочке. Поэтому мы ограничиваемся моделированием с одной степенью свободы, соответствующей радиальному движению. Это движение описывается безразмерной координатой $q$, которая пропорциональна межцентровому расстоянию R. В [26] было показано, что орбитальную степень свободы можно опустить, так как ее учет влияет на сечения в пределах статистических погрешностей, которые в данной работе составляют около 1%.
В [27] было показано, что эффекты памяти в столкновениях тяжелых ионов существенны только вблизи точки касания. В наших расчетах такая конфигурация никогда не достигается, поэтому мы описываем процесс с помощью уравнений типа уравнений Ланжевена с белым шумом и мгновенным трением:
(4)
$dp = {\text{\;}}({{F}_{U}} + {\text{\;}}{{F}_{{cen}}} + {\text{\;}}{{F}_{D}})dt + \sqrt {2D} ~dW,$(8)
${{F}_{D}} = - \frac{p}{{{{m}_{q}}}}{{K}_{R}}{{\left( {\frac{{d{{U}_{n}}}}{{dq}}} \right)}^{2}},$Здесь $p$ – импульс, отвечающий радиальному движению; ${{F}_{U}},$ ${{F}_{{cen}}}$ и ${{F}_{D}}$ – консервативная, центробежная и диссипативная силы соответственно. Последняя связана с потенциалом СиЯВ формулой поверхностного трения (8) [28, 29]. $\hbar L$ представляет собой проекцию орбитального углового момента на ось, перпендикулярную плоскости реакции; ${{m}_{q}}$ – инерционный параметр; ${{K}_{R}}$ обозначает амплитуду коэффициента трения; $D$ – коэффициент диффузии, пропорциональный температуре θ. Случайная сила пропорциональна приращению $dW$ винеровского процесса W; это приращение имеет нулевое среднее и дисперсию равную $dt.$ Уравнения (4), (5) решались численно методом Рунге–Кутта (см. детали в [24, 30]).
Сечения захвата вычислялись по стандартной квантово-механической формуле (см., например, [31])
(10)
${{{{\sigma }}}_{{th}}} = \frac{{\pi {{\hbar }^{2}}}}{{2{{m}_{R}}{{E}_{{c.m.}}}}}\sum\limits_{L = 0}^{{{L}_{{max}}}} {\left( {2L + 1} \right){{T}_{L}}} .$Здесь ${{E}_{{c.m.}}}$ – энергия столкновения в системе центра масс; ${{m}_{R}} = {{{{m}_{n}}{{A}_{P}}{{A}_{T}}} \mathord{\left/ {\vphantom {{{{m}_{n}}{{A}_{P}}{{A}_{T}}} {\left( {{{A}_{P}} + {{A}_{T}}} \right)}}} \right. \kern-0em} {\left( {{{A}_{P}} + {{A}_{T}}} \right)}}$ включает в себя массу нуклона ${{m}_{n}}$ и массовые числа ядра-снаряда (${{A}_{P}}$) и ядра-мишени (${{A}_{T}}$); ${{L}_{{max}}}$ – максимальное значение углового момента, выше которого коэффициент прохождения ${{T}_{L}}$ становится достаточно малым. Коэффициент прохождения является результатом динамического моделирования, описанного выше.
СРАВНЕНИЕ С ЭКСПЕРИМЕНТОМ
Мы вычисляем сечения слияния ${{\sigma }_{{th}}},$ варьируя амплитуду коэффициента трения ${{K}_{R}}$ в формулах (8), (9) для каждой реакции, подобно тому, как это сделано в [7, 24]. Расчетные сечения сравниваются с экспериментальными ${{\sigma }_{{exp}}}$ с помощью формулы (11)
(11)
${{\chi }^{2}} = \frac{1}{\upsilon }\sum\limits_{i = 1}^\upsilon {{{{\left( {\frac{{{{\sigma }_{{ith}}} - {{\sigma }_{{iexp}}}}}{{{{\Delta }}{{\sigma }_{{iexp}}}}}} \right)}}^{2}}} .$Здесь ${{\sigma }_{{ith}}}$ соответствует значению ${{E}_{{c.m.~i~}}},$ а ${{\sigma }_{{iexp}}}$ и ${{\Delta }}{{\sigma }_{{iexp}}}$ – экспериментальное сечение и его погрешность для того же значения энергии столкновения. Оптимальное значение амплитуды коэффициента трения, ${{K}_{{Rm}}},$ соответствует минимуму величины ${{\chi }^{2}},$ $\chi _{m}^{2}.$ Полученные таким образом значения ${{K}_{{Rm}}},$ $\chi _{m}^{2},$ и ${{U}_{{B0}}}$ (высота кулоновского барьера для нулевого углового момента) собраны в табл. 2. Они сравниваются со значениями, найденными в [7]. Оптимальные значения амплитуды коэффициента трения, найденные в настоящей работе, оказываются значительно меньше значений, полученных в [7] потому, что высоты барьеров в настоящей работе получились несколько больше. Значения $\chi _{m}^{2}$ в настоящих ТРСП-расчетах оказываются примерно такими же, как и в [7], не обнаруживая никакой регулярной закономерности.
Рисунок 4 дает визуальное представление о степени согласия расчетных сечений с экспериментальными. На нем показано отношение ${{{{\sigma }_{{th}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{th}}}} {{{\sigma }_{{exp}}}}}} \right. \kern-0em} {{{\sigma }_{{exp}}}}}$ как функция ${{{{U}_{{B0}}}} \mathord{\left/ {\vphantom {{{{U}_{{B0}}}} {{{E}_{{c.m.}}}}}} \right. \kern-0em} {{{E}_{{c.m.}}}}}$ для пяти реакций из табл. 2. Теоретические сечения получены с использованием HS_E NN-сил с оптимальными значениями ${{K}_{{Rm}}}.$ Типичные статистические погрешности ланжевеновских расчетов составляют около 1%. Рисунок 4 показывает довольно хорошее качество теоретического описания данных: из 42 точек только две выходят за пределы 5%-ной полосы.
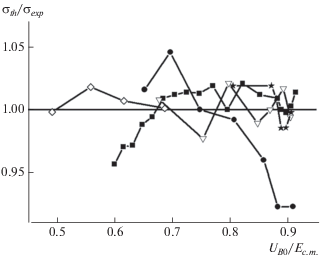
Рис. 4.
Отношение ${{{{\sigma }_{{th}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{th}}}} {{{\sigma }_{{exp}}}}}} \right. \kern-0em} {{{\sigma }_{{exp}}}}}$ как функция ${{{{U}_{{B0}}}} \mathord{\left/ {\vphantom {{{{U}_{{B0}}}} {{{E}_{{c.m.}}}}}} \right. \kern-0em} {{{E}_{{c.m.}}}}}$ для пяти реакций из табл. 2: сплошные квадраты – 16O + 92Zr, открытые треугольники – 16O + 144Sm, сплошные кружки – 12C + 208Pb, сплошные звездочки – 28Si + 92Zr, открытые ромбы – 12C + 144Sm.
ЗАКЛЮЧЕНИЕ
В настоящей работе вычислены сечения слияния для пяти реакций со сферическими ядрами при энергиях столкновения выше кулоновского барьера. Для этого использован ядро-ядерный потенциал, полученный в модели двойной свертки (см. формулу (3)) с нуклон-нуклонными (NN) силами ${{\nu }_{{NN}}},$ основанными на теории релятивистского среднего поля (ТРСП). Эти NN-силы соответствуют NL1, NL2, NL3 и HS наборам параметров ТРСП, которые встречаются в литературе. Использованные для расчетов плотности нуклонов были вычислены в хартри-фоковском подходе с силами Скирма (SKX-параметризация) с учетом тензорного характера сил.
Наши расчеты показали, что два из этих наборов параметров (NL1 и NL3) приводят к полному потенциалу ядро-ядерного взаимодействия (сильное + кулоновское), не имеющему барьера. При учете обменного слагаемого в NN-силах (такого же как в M3Y парижских силах) барьер появляется только для NL2- и HS-наборов параметров. Причину отсутствия/наличия барьера мы видим в скорости роста прямой части NN-сил при уменьшении расстояния между нуклонами. Высоты релятивистских кулоновских барьеров в наших расчетах оказались близки к полученным ранее с использованием M3Y NN-сил.
Ядро-ядерные потенциалы, рассчитанные с использованием HS ТРСП NN-сил, были использованы для вычисления сечений слияния с помощью флуктуационно-диссипативной траекторной модели с поверхностным трением, известной в литературе. Теоретические сечения сравниваются “точка в точку” с высокоточными экспериментальными сечениями (типичная погрешность около 1%) для пяти реакций. Результат сравнения демонстрирует хорошее качество согласия теории с экспериментом: типичный хи-квадрат составляет несколько единиц. Расчеты с NL2-параметрами дают сходный результат (см. [32]).
Список литературы
Reinhard P.G., Rufa M., Maruhn J. et al. // Z. Phys. 1986. A. 323. P. 13.
Hirata D., Toki H., Watabe T. et al. // Phys. Rev. C. 1991. V. 44. P. 1467.
Sugahara Y., Toki H. // Nucl. Phys. A. 1994. V. 579. P. 557.
Newton J.O., Butt R.D., Dasgupta M. et al. // Phys. Lett. B. 2004. V. 586. P. 219.
Newton J.O., Butt R.D., Dasgupta M. et al. // Phys. Rev. C. 2004. V. 70. Art. No. 024605.
Gontchar I.I., Bhattacharya R., Chushnyakova M.V. // Phys. Rev. C. 2014. V. 89. Art. No. 034601.
Chushnyakova M.V., Bhattacharya R., Gontchar I.I. // Phys. Rev. C. 2014. V. 90. Art. No. 017603.
Lahiri C., Biswal S.K., Patra S.K. // Int. J. Mod. Phys. E. 2016. V. 25. Art. No. 1650015 .
Lalazissis G.A., König J., Ring P. // Phys. Rev. C. 1997. V. 55. P. 540.
Horowitz C.J., Serot B.D. // Nucl. Phys. A. 1981. V. 368. P. 503.
Singh B., Bhuyan M., Patra S.K., Gupta R.K. // J. Phys. G. 2012. V. 39. Art. No. 025101.
Bhuyan M., Kumar R. // Phys. Rev. C. 2018. V. 98. Art. No. 054610.
Anantaraman N., Toki H., Bertsch G.F.// Nucl. Phys. A. 1983. V. 398. P. 269.
Gontchar I.I., Hinde D.J., Dasgupta M., Newton J.O. // Phys. Rev. C. 2004. V. 69. Art. No. 024610.
Gontchar I.I., Chushnyakova M.V. // Comput. Phys. Commun. 2010. V. 181. P. 168.
Bhattacharya R. // Nucl. Phys. A. 2013. V. 913. P. 1.
Brown B.A. // Phys. Rev. C. 1998. V. 58. P. 220.
Gasques L.R., Afanasjev A.V., Beard M. et al. // Phys. Rev. C. 2007. V. 76. Art. No. 045802.
Newton J.O., Morton C.R., Dasgupta M. et al. // Phys. Rev. C. 2001. V. 64. Art. No. 064608.
Leigh J.R., Dasgupta M., Hinde D.J. et al. // Phys. Rev. C. 1995. V. 52. P. 3151.
Dasgupta M., Hinde D.J., Diaz-Torres A. et al. // Phys. Rev. Lett. 2007. V. 99. Art. No. 192701.
Kossakowski R., Jastrzbski J., Rymuza P. et al. // Phys. Rev. C. 1985. V. 32. P. 1612.
Zagrebaev V.I., Denikin A.S., Karpov A.V. et al. // Nucl. Instr. Meth. Phys. Res. A. 2017. V. 859. P. 112.
Chushnyakova M.V., Gontchar I.I. // Phys. Rev. C. 2013. V. 87. Art. No. 014614.
Fröbrich P., Gontchar I.I. // Phys. Rep. 1998. V. 292. P. 131.
Chushnyakova M.V., Gontchar I.I. // J. Phys. G. 2013. V. 40. Art. No. 095108.
Wen K., Sakata F., Li Z.-X. et al. // Phys. Rev. Lett. 2013. V. 111. Art. No. 012501.
Gross D.H.E., Kalinowski H. // Phys. Rep. 1978. V. 45. P. 175.
Fröbrich P. // Phys. Rep. 1984. V. 116. P. 337.
Gegechkori A.E., Anischenko Y.A., Nadtochy P.N., Adeev G.D. // Phys. Atom. Nucl. 2008. V. 71. P. 2007.
Fröbrich P., Lipperheide R. Theory of nuclear reactions. Oxford: Clarendon Press, 1996.
Chushnyakova M.V., Gontchar I.I., Khmyrova N.A. // J. Phys. G. 2021. V. 48. Art. № 015101.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


