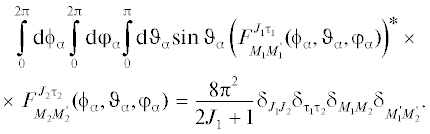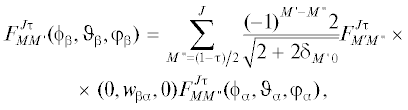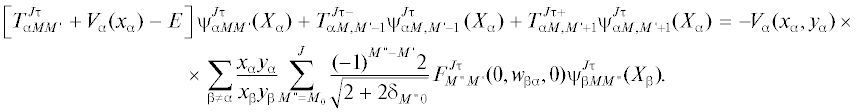Известия РАН. Серия физическая, 2021, T. 85, № 5, стр. 723-727
Теоретическое исследование слабосвязанных трехатомных систем с помощью уравнений Фаддеева в представлении полного орбитального момента
В. А. Градусов 1, *, В. А. Руднев 1, Е. А. Яревский 1, С. Л. Яковлев 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Санкт-Петербургский государственный университет”
Санкт-Петербург, Россия
* E-mail: v.gradusov@spbu.ru
Поступила в редакцию 20.11.2020
После доработки 28.12.2020
Принята к публикации 27.01.2021
Аннотация
Представлены результаты расчетов спектров слабосвязанных трехатомных молекулярных комплексов – тримера гелия и молекул гелий–гелий–щелочной металл. Расчеты проведены на основе уравнений Фаддеева в представлении полного орбитального момента. Подтверждено наличие возбужденных состояний с ненулевым полным орбитальным моментом у некоторых молекул.
ВВЕДЕНИЕ
Непрекращающийся интерес к теоретическому и экспериментальному исследованию слабосвязанных трехатомных молекул обусловлен, прежде всего, их связью с эффектом Ефимова [1] и возможностью исследования универсальных закономерностей в системах квантовых частиц [2]. Для теоретического описания таких систем, как правило, выбирается модель трех взаимодействующих бесструктурных атомов. Достоверность модели оправдывается существованием хороших полуэмпирических потенциалов взаимодействия атомов, основанных на приближении потенциалов, получаемых в квантово-химических расчетах.
Хотя наиболее изученной слабосвязанной трехатомной молекулой является тример гелия [3], представляют интерес также и другие молекулярные комплексы – такие, как, например, гелий-гелий-щелочной металл [4, 5]. Хотя энергии основных состояний с нулевым полным орбитальным моментом этих систем крайне близки к порогу развала [6], некоторые из них имеют также и возбужденные связанные состояния, в том числе со значением момента, большим нуля. Это было впервые установлено в расчетах, представленных в недавней работе [4]. Представляется важным подтвердить существование этих состояний в независимых расчетах. Однако, насколько известно авторам настоящей статьи, соответствующие результаты до сих пор представлены не были. Причиной этого может быть большая сложность этих расчетов. Для их проведения требуется подход, комбинирующий хороший теоретический метод и эффективный вычислительный алгоритм.
Недавно нами был предложен и реализован [7] такой подход, основанный на решении уравнений Фаддеева–Меркурьева [8] в представлении полного орбитального момента [9]. В случае отсутствия в системе кулоновского взаимодействия уравнения Фаддеева–Меркурьева сводятся к обычным уравнениям Фаддеева. Эти уравнения, как известно, описывают связанные состояния и состояния рассеяния трех квантовых частиц. Тестовые расчеты [7] показали, что наш подход позволяет проводить высокоточные расчеты энергий связанных состояний с достаточно высокими значениями полного орбитального момента.
В данной работе мы применяем описанный выше подход к вычислению связанных состояний различных слабосвязанных молекул. В частности, мы исследуем вопрос о существовании возбужденных состояний с ненулевым полным орбитальным моментом комплексов гелий–гелий–щелочной металл.
УРАВНЕНИЯ ФАДДЕЕВА
Уравнения Фаддеева для трех бесспиновых нерелятивистских квантовых частиц имеют вид
(1)
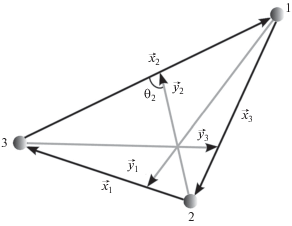
$\begin{gathered} \{ {{T}_{{{\alpha }}}} + {{V}_{{{\alpha }}}}({{x}_{{{\alpha }}}}) - E\} {{\psi }_{{{\alpha }}}}({{{\vec {x}}}_{{{\alpha }}}},{{{\vec {y}}}_{{{\alpha }}}}) = - {{V}_{{{\alpha }}}}({{x}_{{{\alpha }}}},{{y}_{{{\alpha }}}}) \times \\ \times \,\,\sum\limits_{{{\beta }} \ne {{\alpha }}} {{{\psi }_{{{\beta }}}}} ({{{\vec {x}}}_{{{\beta }}}},{{{\vec {y}}}_{{{\beta }}}}),\,\,\,\,\alpha = 1,2,3. \\ \end{gathered} $Они описывают связанные состояния и состояния рассеяния с энергией E частиц, имеющих массы ${{m}_{{{\alpha }}}},$ в системе центра масс [8]. В дальнейшем будем считать, что встречающиеся в обозначениях греческие индексы $\alpha ,$ $\beta ,$ $\gamma $ нумеруют частицы и пробегают значения {1, 2, 3}. Кроме того, парой $\alpha $ будем называть пару частиц с номерами, дополняющими номер $\alpha .$ Например, парой 1 называется пара частиц 2 и 3. Положения частиц в системе центра масс описываются приведенными координатами Якоби ${{\vec {x}}_{{{\alpha }}}},$ ${{\vec {y}}_{{{\alpha }}}},$ которые представляют собой умноженные на величины $\sqrt {2{{\mu }_{{{\alpha }}}}} $ и $\sqrt {2{{\mu }_{{{{\alpha }}({{\beta \gamma }})}}}} $ векторы Якоби, изображенные на рис. 1. Здесь приведенные массы выражаются формулами
(2)
${{\mu }_{{{\alpha }}}} = \frac{{{{m}_{{{\beta }}}}{{m}_{{{\gamma }}}}}}{{{{m}_{{{\beta }}}} + {{m}_{{{\gamma }}}}}},\,\,\,{{\mu }_{{{{\alpha }}({{\beta \gamma }})}}} = \frac{{{{m}_{{{\alpha }}}}({{m}_{{{\beta }}}} + {{m}_{{{\gamma }}}})}}{{{{m}_{{{\alpha }}}} + {{m}_{{{\beta }}}} + {{m}_{{{\gamma }}}}}}.$Векторы Якоби описывают относительные положения частиц пары $\alpha $ и частицы $\alpha $ и центра масс пары $\alpha ,$ соответственно. Три возможных набора приведенных координат Якоби связаны между собой ортогональными преобразованиями [8]. В дальнейшем предполагается, что в формулах координаты ${{\vec {x}}_{{{\beta }}}},$ ${{\vec {y}}_{{{\beta }}}}$ выражены через координаты ${{\vec {x}}_{{{\alpha }}}},$ ${{\vec {y}}_{{{\alpha }}}}.$ Операторы кинетической энергии даются выражениями ${{T}_{{{\alpha }}}} = - {{\Delta }_{{{{{\bar {x}}}_{{{\alpha }}}}}}} - {{\Delta }_{{{{{\bar {y}}}_{{{\alpha }}}}}}}.$ Взаимодействие частиц пары $\alpha $ описывается центральным короткодействующим (убывающим быстрее ${1 \mathord{\left/ {\vphantom {1 {x_{{{\alpha }}}^{2}}}} \right. \kern-0em} {x_{{{\alpha }}}^{2}}}$ при ${{x}_{\alpha }} \to \infty $) потенциалом ${{V}_{{{\alpha }}}}({{x}_{{{\alpha }}}}).$ Система уравнений (1) строго эквивалентна уравнению Шрёдингера [8], решение которого – волновая функция – может быть получена по формуле $\Psi = \sum\nolimits_{{\alpha }} {{{\psi }_{{{\alpha }}}}} .$ Решения уравнений Фаддеева ${{\psi }_{{{\alpha }}}}$ называются компонентами волновой функции. Для расчетов связанных состояний уравнения (1) дополняются нулевыми граничными условиями типа Дирихле ${{\psi }_{{{\alpha }}}}({{x}_{{{\alpha }}}},{{y}_{{{\alpha }}}}) \to 0$ при ${{x}_{{{\alpha }}}}$ или ${{y}_{{{\alpha }}}} \to \infty .$ Это дает задачу на собственные значения, из которой определяется дискретный спектр энергий трехчастичной системы.
Каждое из уравнений системы (1) представляет собой шестимерное уравнение в частных производных. Решать такие уравнения даже на современных компьютерах затруднительно. По этой причине для проведения расчетов мы далее переходим к уравнениям Фаддеева, записанным в представлении полного орбитального момента. Для получения этих уравнений компоненты ${{\psi }_{{{\alpha }}}}$ разлагаются в ряд по собственным функциям оператора квадрата полного орбитального момента системы частиц. Этот подход, предложенный в работе [9], приводит к конечной системе связанных трехмерных уравнений в частных производных. В следующей части настоящего раздела мы кратко описываем вывод этих уравнений.
Прежде всего, введем новые кинематические координаты (${{X}_{{{\alpha }}}},$ ${{\Omega }_{{{\alpha }}}}$) в шестимерном конфигурационном пространстве задачи. Координаты Xα = = $\{ {{x}_{{{\alpha }}}},{{y}_{{{\alpha }}}},{{z}_{{{\alpha }}}}\} $ описывают положения частиц в плоскости, их содержащей. Здесь zα = = ${{({{{\vec {x}}}_{{{\alpha }}}},{{{\vec {y}}}_{{{\alpha }}}})} \mathord{\left/ {\vphantom {{({{{\vec {x}}}_{{{\alpha }}}},{{{\vec {y}}}_{{{\alpha }}}})} {({{x}_{{{\alpha }}}}{{y}_{{{\alpha }}}})}}} \right. \kern-0em} {({{x}_{{{\alpha }}}}{{y}_{{{\alpha }}}})}}$ – косинус угла между векторами ${{\vec {x}}_{{{\alpha }}}}$ и ${{\vec {y}}_{{{\alpha }}}}.$ Оставшиеся три координаты ${{\Omega }_{{{\alpha }}}} = \{ {{\phi }_{{{\alpha }}}},{{\vartheta }_{{{\alpha }}}},{{\varphi }_{{{\alpha }}}}\} $ описывают положение указанной плоскости в пространстве. Они определяются как три угла Эйлера, вращение на которые переводит некоторую лабораторную систему координат в связанную с частицами прямоугольную систему координат, в которой вектор ${{\vec {y}}_{{{\alpha }}}}$ расположен вдоль оси z, а вектор ${{\vec {x}}_{{{\alpha }}}}$ расположен в плоскости xz.
В этих новых координатах уравнения Фаддеева принимают вид
(3)
$\begin{gathered} \{ {{T}_{{{\alpha }}}} + {{V}_{{{\alpha }}}}({{x}_{{{\alpha }}}}) - E\} {{\psi }_{{{\alpha }}}}({{X}_{{{\alpha }}}},{{\Omega }_{{{\alpha }}}}) = - {{V}_{{{\alpha }}}}({{x}_{{{\alpha }}}},{{y}_{{{\alpha }}}}) \times \\ \times \,\,\sum\limits_{{{\beta }} \ne {{\alpha }}} {{{\psi }_{{{\beta }}}}} ({{X}_{{{\beta }}}},{{\Omega }_{{{\beta }}}}),\,\,\,\,\alpha = 1,2,3. \\ \end{gathered} $Здесь ${{\psi }_{{{\alpha }}}}({{X}_{{{\alpha }}}},{{\Omega }_{{{\alpha }}}})$ обозначают компоненты, выраженные в новых переменных. Оператор кинетической энергии в новых переменных имеет вид
(4)
$\begin{gathered} {{T}_{{{\alpha }}}} = - \frac{1}{{y_{{{\alpha }}}^{2}}}\frac{\partial }{{\partial {{y}_{{{\alpha }}}}}}y_{{{\alpha }}}^{2}\frac{\partial }{{\partial {{y}_{{{\alpha }}}}}} - \\ - \,\,\frac{1}{{x_{{{\alpha }}}^{2}}}\frac{\partial }{{\partial {{x}_{{{\alpha }}}}}}x_{{{\alpha }}}^{2}\frac{\partial }{{\partial {{x}_{{{\alpha }}}}}} - \left( {\frac{1}{{y_{\alpha }^{2}}} + \frac{1}{{x_{\alpha }^{2}}}} \right) \times \\ \times \,\,\left( {\frac{1}{{\sin {{\theta }_{{{\alpha }}}}}}\frac{\partial }{{\partial {{\theta }_{{{\alpha }}}}}}\sin {{\theta }_{{{\alpha }}}}\frac{\partial }{{\partial {{\theta }_{{{\alpha }}}}}} + \frac{1}{{{{{\sin }}^{2}}{{\theta }_{{{\alpha }}}}}}\frac{{{{\partial }^{2}}}}{{\partial \varphi _{{{\alpha }}}^{2}}}} \right) + \frac{{{{{\mathbf{J}}}^{2}} - {{{\mathbf{K}}}_{{{\alpha }}}}}}{{y_{{{\alpha }}}^{2}}}. \\ \end{gathered} $Здесь первые слагаемые действуют по переменным ${{X}_{{{\alpha }}}},$ последнее слагаемое действует по всем шести кинематическим переменным, однако выражается через операторы$,$ имеющие ясный физический смысл. В частности, оператор
(5)
$\begin{gathered} {{{\mathbf{J}}}^{2}} = - \left[ {\frac{1}{{\sin {{\vartheta }_{{{\alpha }}}}}}\frac{\partial }{{\partial {{\vartheta }_{{{\alpha }}}}}}\sin {{\vartheta }_{{{\alpha }}}}\frac{\partial }{{\partial {{\vartheta }_{{{\alpha }}}}}} + \frac{1}{{{{{\sin }}^{2}}{{\vartheta }_{{{\alpha }}}}}}} \right. \times \\ \left. { \times \,\,\left( {\frac{{{{\partial }^{2}}}}{{\partial \phi _{{{\alpha }}}^{2}}} - 2\cos {{\vartheta }_{{{\alpha }}}}\frac{{{{\partial }^{2}}}}{{\partial {{\phi }_{{{\alpha }}}}\partial {{\varphi }_{{{\alpha }}}}}} + \frac{{{{\partial }^{2}}}}{{\partial \varphi _{{{\alpha }}}^{2}}}} \right)} \right] \\ \end{gathered} $представляет собой оператор квадрата полного орбитального момента системы, а оператор
(6)
${{{\mathbf{K}}}_{{{\alpha }}}} = \frac{\partial }{{\partial {{\theta }_{{{\alpha }}}}}}\left( {{\mathbf{J}}_{{{\alpha }}}^{{( + )}} + {\mathbf{J}}_{{{\alpha }}}^{{( - )}}} \right) + {\text{ctg}}{{\theta }_{{{\alpha }}}}\left( {{\mathbf{J}}_{{{\alpha }}}^{{( + )}} - {\mathbf{J}}_{{{\alpha }}}^{{( - )}}} \right) + 2{\mathbf{J}}_{{z{\kern 1pt} '}}^{2}$выражается через операторы, связанные с проекциями полного орбитального момента на различные оси
(7)
$\begin{gathered} {\mathbf{J}}_{{{\alpha }}}^{{( \pm )}} = \mp {{{\text{e}}}^{{ \mp {\text{i}}{{{{\varphi }}}_{{{\alpha }}}}}}}\left[ { \pm \frac{\partial }{{\partial {{\vartheta }_{{{\alpha }}}}}} + \frac{{\text{i}}}{{\sin {{\vartheta }_{{{\alpha }}}}}}\frac{\partial }{{\partial {{\phi }_{{{\alpha }}}}}} - {\text{ictg}}{{\vartheta }_{{{\alpha }}}}\frac{\partial }{{\partial {{\varphi }_{{{\alpha }}}}}}} \right], \\ {{{\mathbf{J}}}_{{z{\kern 1pt} '}}} = {{ - {\text{i}}\partial } \mathord{\left/ {\vphantom {{ - {\text{i}}\partial } {\partial {{\varphi }_{{{\alpha }}}}}}} \right. \kern-0em} {\partial {{\varphi }_{{{\alpha }}}}}}. \\ \end{gathered} $В качестве следующего шага разлагаем компоненты волновой функции в ряды
(8)
$\begin{gathered} {{\psi }_{{{\alpha }}}}({{X}_{{{\alpha }}}},{{\Omega }_{{{\alpha }}}}) = \\ = \sum\limits_{J = 0}^{ + \infty } {\sum\limits_{{{\tau }} = \pm 1} {\sum\limits_{M = - J}^J {\sum\limits_{M{\kern 1pt} ' = {{M}_{0}}}^J {\frac{{\psi _{{\alpha MM{\kern 1pt} '}}^{{J{{\tau }}}}({{X}_{{{\alpha }}}})}}{{{{x}_{{{\alpha }}}}{{y}_{{{\alpha }}}}}}} } } } F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}({{\phi }_{{{\alpha }}}},{{\vartheta }_{{{\alpha }}}},{{\varphi }_{{{\alpha }}}}) \\ \end{gathered} $по базису функций $F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}},$ зависящих от углов Эйлера. Коэффициенты разложения $\psi _{{{{\alpha }}MM{\kern 1pt} '}}^{{J{{\tau }}}}$ будем называть парциальными компонентами волновой функции. Функции $F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}$ являются линейными комбинациями D-функций Вигнера
(9)
$\begin{gathered} F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}({{\Omega }_{{{\alpha }}}}) = \frac{1}{{\sqrt {2 + 2{{\delta }_{{M{\kern 1pt} '0}}}} }} \times \\ \times \,\,\left( {D_{{MM{\kern 1pt} '}}^{J}({{\Omega }_{{{\alpha }}}}) + \tau {{{( - 1)}}^{{M{\kern 1pt} '}}}D_{{M, - M{\kern 1pt} '}}^{J}({{\Omega }_{{{\alpha }}}})} \right), \\ \end{gathered} $определенными как в [10, 11]. Функция $F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}$ является одновременно собственной функцией операторов квадрата и проекции полного орбитального момента, а также оператора $P$ инверсии координат частиц
(10)
$\begin{gathered} {{{\mathbf{J}}}^{2}}F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}} = J(J + 1)F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}},\,\,\,\,{{{\mathbf{J}}}_{z}}F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}} = - MF_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}, \\ {\mathbf{P}}F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}} = \tau {{( - 1)}^{J}}F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}. \\ \end{gathered} $Она описывает состояние системы со значениями полного орбитального момента J, его проекции $M$ и пространственной четности $\tau = \pm 1.$ Функции $F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}$ удовлетворяют условиям ортогональности
Кроме того, набор функций с целыми $J \geqslant 0,$ $\tau = \pm 1,$ $\left| M \right| \leqslant J$ и ${{(1 - \tau )} \mathord{\left/ {\vphantom {{(1 - \tau )} 2}} \right. \kern-0em} 2} \leqslant M{\kern 1pt} ' \leqslant J$ образуют базис в пространстве квадратично интегрируемых функций со значениями аргументов в области $[0,2\pi ] \times [0,\pi ] \times [0,2\pi ].$
Наконец, функции $F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}$ от углов Эйлера, определенных относительно двух различных наборов координат Якоби $\{ {{\vec {x}}_{{{\alpha }}}},{{\vec {y}}_{{{\alpha }}}}\} $ и $\{ {{\vec {x}}_{{{\beta }}}},{{\vec {y}}_{{{\beta }}}}\} ,$ связаны соотношениями
в которых кинематический угол ${{w}_{{{{\alpha \beta }}}}}$ определяется выражением
(13)
${{w}_{{{{\beta \alpha }}}}} = \left\{ {\begin{array}{*{20}{l}} {\arccos \frac{{ - {{s}_{{{{\beta \alpha }}}}}{{x}_{{{\alpha }}}}{{z}_{{{\alpha }}}} + {{c}_{{{{\beta \alpha }}}}}{{y}_{{{\alpha }}}}}}{{{{y}_{{{\beta }}}}}},\,\,\,{\text{если}}\,\,\,(\beta ,\alpha ) = (2,1),\,\,(3,2),\,\,(1,3),} \\ {2\pi - \arccos \frac{{ - {{s}_{{{{\beta \alpha }}}}}{{x}_{{{\alpha }}}}{{z}_{{{\alpha }}}} + {{c}_{{{{\beta \alpha }}}}}{{y}_{{{\alpha }}}}}}{{{{y}_{{{\beta }}}}}}\,\,\,{\text{в}}\,\,{\text{остальных}}\,\,{\text{случаях}},} \end{array}} \right.$в котором область значений арккосинуса полагается равной $[0,\pi ].$
Подставляя ряды (8) в уравнения (3) и проектируя их на базисные функции $F_{{MM{\kern 1pt} '}}^{{J{{\tau }}}},$ получаем систему трехмерных уравнений Фаддеева в представлении полного орбитального момента, связывающих парциальные компоненты
Здесь операторы кинетической энергии имеют вид
(15)
$\begin{gathered} T_{{{{\alpha }}MM{\kern 1pt} '}}^{{J{{\tau }}}} = - \frac{{{{\partial }^{2}}}}{{\partial y_{{{\alpha }}}^{2}}} + \frac{1}{{y_{{{\alpha }}}^{2}}}\left( {J(J + 1) - 2{{M}^{{'2}}}} \right) - \frac{{{{\partial }^{2}}}}{{\partial x_{{{\alpha }}}^{2}}} - \\ - \,\,\left( {\frac{1}{{y_{{{\alpha }}}^{2}}} + \frac{1}{{x_{{{\alpha }}}^{2}}}} \right)\left( {\frac{\partial }{{\partial {{z}_{{{\alpha }}}}}}(1 - z_{{{\alpha }}}^{2})\frac{\partial }{{\partial {{z}_{{{\alpha }}}}}} - \frac{{{{M}^{{'2}}}}}{{1 - z_{{{\alpha }}}^{2}}}} \right), \\ T_{{{{\alpha }}M,M{\kern 1pt} ' \pm 1}}^{{J{{\tau }} \pm }} = \pm \frac{1}{{y_{{{\alpha }}}^{2}}}{{\lambda }^{{J, \pm M{\kern 1pt} '}}}\sqrt {1 + {{\delta }_{{M{\kern 1pt} '0(1)}}}} \times \\ \times \,\,\left[ { - \sqrt {1 - z_{{{\alpha }}}^{2}} \frac{\partial }{{\partial {{z}_{{{\alpha }}}}}} \pm (M{\kern 1pt} ' \pm 1)\frac{{{{z}_{{{\alpha }}}}}}{{\sqrt {1 - z_{{{\alpha }}}^{2}} }}} \right]. \\ \end{gathered} $Важнейшим свойством системы (14) является то, что уравнения, в которых участвуют парциальные компоненты $\psi _{{{{\alpha }}MM{\kern 1pt} '}}^{{J{{\tau }}}}$ с различными индексами $J,$ $M$ и $\tau ,$ образуют независимые системы уравнений. Это является прямым следствием того, что для рассматриваемых трехчастичных систем полный орбитальный момент, его проекция и пространственная четность являются сохраняющимися величинами. Таким образом, для вычисления спектра системы при данных значениях $J,$ $M$ и $\tau $ требуется решить граничную задачу с $3{{n}_{M}}$ уравнениями (14), где
(16)
${{n}_{M}}{\text{ }} = {\text{ }}J - {{\left( {1 - \tau } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \tau } \right)} 2}} \right. \kern-0em} 2} + 1$обозначает количество возможных значений индекса $M{\kern 1pt} '$ парциальных компонент $\psi _{{{{\alpha }}MM{\kern 1pt} '}}^{{J{{\tau }}}}$ при данных $J$ и $\tau .$ К нулевым асимптотическим граничным условиям типа Дирихле добавляются также нулевые условия на прямых ${{x}_{{{\alpha }}}} = 0$ и ${{y}_{{{\alpha }}}} = 0.$
В случае, когда в системе имеются тождественные частицы, количество уравнений может быть существенно сокращено за счет дополнительной симметрии парциальных компонент. В частности, в случае тождественности частиц 1 и 2 выполняется
(17)
$\begin{gathered} \psi _{{2MM{\kern 1pt} '}}^{{J{{\tau }}}}({{x}_{2}},{{y}_{2}},{{z}_{2}}) = p{{( - 1)}^{{M{\kern 1pt} '}}}\psi _{{1MM{\kern 1pt} '}}^{{J{{\tau }}}}({{x}_{2}},{{y}_{2}}, - {{z}_{2}}), \\ \psi _{{3MM{\kern 1pt} '}}^{{J{{\tau }}}}({{x}_{3}},{{y}_{3}},{{z}_{3}}) = p{{( - 1)}^{{M{\kern 1pt} '}}}\psi _{{3MM{\kern 1pt} '}}^{{J{{\tau }}}}({{x}_{3}},{{y}_{3}}, - {{z}_{3}}), \\ \end{gathered} $а в случае тождественности всех трех частиц
(18)
$\psi _{{1(2,3)MM{\kern 1pt} '}}^{{J{{\tau }}}}({{x}_{1}},{{y}_{1}},{{z}_{1}}) = p{{( - 1)}^{{M{\kern 1pt} '}}}\psi _{{1MM{\kern 1pt} '}}^{{J{{\tau }}}}({{x}_{1}},{{y}_{1}}, - {{z}_{1}}).$Здесь $p = \pm 1$ обозначает симметрию/антисимметрию волновой функции системы относительно перестановки координат тождественных частиц. Число уравнений в этих двух случаях сокращается до $2{{n}_{M}}$ и ${{n}_{M}},$ соответственно.
Алгоритм численного решения уравнений (14) основан на методе сплайн-коллокации и изложен в статье [7], к которой мы отсылаем заинтересованного в его подробностях читателя.
РЕЗУЛЬТАТЫ
В данном разделе представлены результаты расчетов спектров слабосвязанных молекул 4He3 и 4He2X, где X – атом щелочного металла 6Li или 23Na. В расчетах для описания взаимодействий гелий-щелочной металл мы использовали потенциалы KTTY [12], в качестве потенциала пары гелий-гелий был выбран TTY [13]. Они представляют собой модифицированные потенциалы Леннарда-Джонса.
В расчетах мы использовали специально подобранную по методике работы [14] сетку узлов сплайна по переменной ${{x}_{{{\alpha }}}}.$ Она подбирается как сетка, оптимальная для расчета связанных состояний частиц пары $\alpha $ с помощью радиального уравнения Шрёдингера. Технически она получается из сетки узлов, равноотстоящих на заданном интервале, по формуле ${{x}_{i}} = {{x}_{{max}}}\chi ({i \mathord{\left/ {\vphantom {i N}} \right. \kern-0em} N}),$ $i = 0, \ldots ,N$ при помощи монотонного отображения $\chi :[0,1] \to [0,1].$ Это отображение, в свою очередь, выражается через так называемую градуировочную функцию $\varepsilon (x)$ по формуле
(19)
${{\chi }^{{ - 1}}}(u) = \frac{{\int\limits_0^{u{{x}_{{max}}}} {{\text{d}}x\varepsilon (x)} }}{{\int\limits_0^{{{x}_{{max}}}} {{\text{d}}x{\mkern 1mu} \varepsilon (x)} }}.$В случае используемого в расчетах базиса $S_{5}^{3}$ сплайнов градуировочная функция вычисляется по формуле
(20)
$\varepsilon (x) = {{\left( {\sum\limits_{m = 1}^n {{{{\left| {\frac{{{{d}^{6}}}}{{d{{x}^{6}}}}{{\varphi }_{m}}(x)} \right|}}^{2}}} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 {13}}} \right. \kern-0em} {13}}}}},$В табл. 1 для иллюстрации возможностей нашего подхода представлены результаты сходимости значений энергии основного состояния с $J = 0,$ $p = 1$ молекулы 4He3, известной с хорошей точностью [3], в зависимости от размера базиса сплайнов, по которому разлагается парциальная компонента. Из представленных результатов видно, что в расчетах удается достигнуть точной 4–5 значащей цифры значения энергии.
Таблица 1.
Сходимость значений энергии основного состояния молекулы 4He3 в зависимости от количества базисных функций по переменным xα, yα, zα. Эталонное значение [10]: –4.00722 ⋅ 10–7 а. е.
| Размер базиса | E, 10–7 а.е. |
|---|---|
| (73, 118, 15) | –4.01966 |
| (88, 148, 18) | –4.00865 |
| (103, 178, 21) | –4.00824 |
| (118, 208, 24) | –4.00755 |
| (148, 268, 30) | –4.00738 |
В табл. 2 мы приводим полученные с помощью нашего подхода и представленные в работе [4] значения энергий основного и возбужденного состояний комплексов 4He26Li и 4He223Na. Наши результаты подтверждают существование связанного состояния с $J = 1$ у молекулы 4He223Na. Поскольку в [4] был использован другой потенциал пары гелий-гелий, можно говорить лишь о качественном сравнении значений энергии. Из представленных результатов можно заключить, что спектр в достаточной степени независим от используемых потенциальных моделей.
Таблица 2.
Значения энергий связанных состояний молекул $^{{\text{4}}}{\text{He}}_{2}^{6}{\text{Li}}$ и $^{{\text{4}}}{\text{He}}_{2}^{{23}}{\text{Na}}$
| Молекула | $\left( {J,{\text{ }}p,{\text{ }}n} \right)$ | E, 10–7 а.е. | $E$, 10–7 а.е. [4] |
|---|---|---|---|
| 4He26Li | (0, +1, 0) | –1.812 | –1.865 |
| 4He26Li | (0, +1, 1) | –0.0614 | –0.0662 |
| 4He223Na | (0, +1, 0) | –4.780 | –4.835 |
| 4He223Na | (1, —1, 0) | –1.98 | –1.963 |
ЗАКЛЮЧЕНИЕ
Представленные в статье результаты подтвердили эффективность подхода, основанного на использовании уравнений Фаддеева в представлении полного орбитального момента. В частности, нам удалось подтвердить существование возбужденного связанного состояния с $J = 1$ молекулы 4He223Na. Наш подход мы предполагаем в дальнейшем использовать для расчетов состояний рассеяния с $J \geqslant 0$ в трехчастичных системах.
Работа Градусова В.А. поддержана РНФ (проект № 19-72-00076). Работа Руднева В.А., Яревского Е.А. и Яковлева С.Л. поддержана РФФИ (проект № 18-02-00492).
Список литературы
Efimov V. // Phys. Lett. B. 1970. V. 33. No. 8. P. 563.
Roudnev V., Cavagnero M. // Phys. Rev. Lett. 2012. V. 108. № 11. Art. No. 110402.
Roudnev V., Cavagnero M. // J. Phys. B. 2012. V. 45. No. 2. Art. No. 025101.
Suno H., Hiyama E., Kamimura M. // Few-Body Syst. 2013. V. 54. P. 1557.
Korobitsin A.A., Kolganova E.A. // Springer Proc. Phys. 2020. V. 238. P. 35.
Stipanović P., Vranješ Markić L., Zarić D. et al. // J. Chem. Phys. 2017. V. 146. Art. No. 014305.
Gradusov V.A., Roudnev V.A., Yarevsky E.A. et al. // arXiv: 2005.05398. 2020.
Меркурьев С.П., Фаддеев Л.Д. Квантовая теория рассеяния для систем нескольких частиц. М.: Наука, 1985.
Kostrykin V.V., Kvitsinsky A.A., Merkuriev S.P. // Few-Body Syst. 1989. V. 6. P. 97.
Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Т. 1. М.: Мир, 1984.
Варшалович Д.А., Москалев А.Н., Херсонский В.К. Квантовая теория углового момента. Ленинград: Наука, 1975.
Kleinekathöfer U., Lewerenz M., Mladenović M. // Phys. Rev. Lett. 1999. V. 83. No. 23. P. 4717.
Tang K.T., Toennies J.P., Yiu C.L. // Phys. Rev. Lett. 1995. V. 74. No. 9. P. 1546.
Roudnev V., Cavagnero M. // Comp. Phys. Commun. 2011. V. 182. P. 2099.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая