Известия РАН. Серия физическая, 2021, T. 85, № 6, стр. 854-862
Определение и компенсация перекоса осей трехкоординатных систем позиционирования с помощью метода акустической голографии
Д. А. Николаев 1, *, С. А. Цысарь 1, О. А. Сапожников 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”, физический факультет
Москва, Россия
* E-mail: da.nikolaev@physics.msu.ru
Поступила в редакцию 09.12.2020
После доработки 25.01.2021
Принята к публикации 26.02.2021
Аннотация
Для измерений акустических полей широко применяются автоматические системы позиционирования. На практике при механической сборке и эксплуатации ортогональность механических осей систем может нарушаться, что приводит к заметным ошибкам в определении структуры поля. Приводятся результаты исследования нового прецизионного способа измерения углов между механическими осями и коррекции вносимых ими ошибок с помощью метода акустической голографии.
ВВЕДЕНИЕ
Задачи, связанные с использованием акустических и, в частности, ультразвуковых (УЗ) полей, опираются на предварительные данные о пространственно-временной структуре поля, которые должны быть известны с максимально возможной точностью [1]. Для нахождения пространственной структуры УЗ поля можно проводить измерения параметров волны с помощью приемника (гидрофона или микрофона), перемещающегося от точки к точке в исследуемой трехмерной области пространства. Альтернативный, более быстрый способ записи структуры поля может быть основан на методе акустической голографии, согласно которому для получения информации о структуре поля в пространстве достаточно провести регистрацию акустического сигнала в двумерной области – в пределах пересекаемого УЗ пучком участка поверхности [2].
В любом случае указанные измерения требуют регистрации сигнала в большом количестве точек пространства. Поэтому на практике акустический приемник последовательно устанавливается в заданные точки пространства с помощью системы позиционирования (позиционера) с компьютерным управлением. Позиционеры, тем самым, являются важной частью измерительных установок. В таких системах, как правило, осуществляется прецизионное перемещение используемого устройства вдоль некоторых линейных направляющих с использованием шаговых двигателей. В системах 3-мерного позиционирования имеется три таких направляющих. Они располагаются взаимно перпендикулярно, образуя декартову систему механических осей.
При сборке позиционера не всегда можно гарантировать перпендикулярность механических осей с необходимой точностью. Кроме того, за время эксплуатации системы возможно появление дополнительного отклонения осей. Поскольку интерпретация результатов, полученных с использованием таких систем, проводится в предположении взаимной перпендикулярности механических осей, то существующее в действительности неизвестное отклонение осей от ортогональности может привести к появлению систематической ошибки в позиционировании приемника и, как следствие, к неточному пространственному измерению характеристик акустического поля [3]. Так, например, использование данных для описания пространственной структуры поля, полученных при измерениях в неортогональной системе координат (СК), в случае терапевтического применения УЗ может вызвать повреждение здоровых тканей пациента [4], а в задачах диагностики [5] привести к неточному определению координат акустических рассеивателей.
Если углы перекоса механических осей позиционера известны, то нетрудно провести коррекцию результатов измерений и тем самым избежать ошибок. Углы между механическими осями можно найти с помощью прямого измерения тем или иным измерительным устройством. Однако такое измерение требует привлечения дополнительного оборудования, что зачастую неудобно. Кроме того, довольно сложно гарантировать достаточную точность, особенно в небольших системах позиционирования с узким диапазоном перемещения вдоль измерительных осей. В настоящей работе предлагается новый прецизионный способ определения углов между механическими осями, основанный на методе акустической голографии. Способ перекликается с подходом, использованным в работе [6] для характеризации акустических свойств материалов.
ТЕОРИЯ
Перекос механических осей системы позиционирования относительно ортогональной СК будем описывать тремя углами ${{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},{{{{\alpha }}}_{3}}$ (рис. 1а). Будем помечать тильдой координаты вдоль перекошенных осей, т.е. осей системы позиционирования. При задании указанных углов будем считать, что оси $0x$ и $0\tilde {x}$ совпадают, ось $0\tilde {y}$ расположена в плоскости (x, y) и образует с осью 0y угол ${{{{\alpha }}}_{3}},$ а направление оси $0\tilde {z}$ задается углами ${{{{\alpha }}}_{1}}$ и ${{{{\alpha }}}_{2}}$ ее наклона относительно плоскостей $\left( {y,z} \right)$ и $\left( {x,z} \right),$ соответственно.
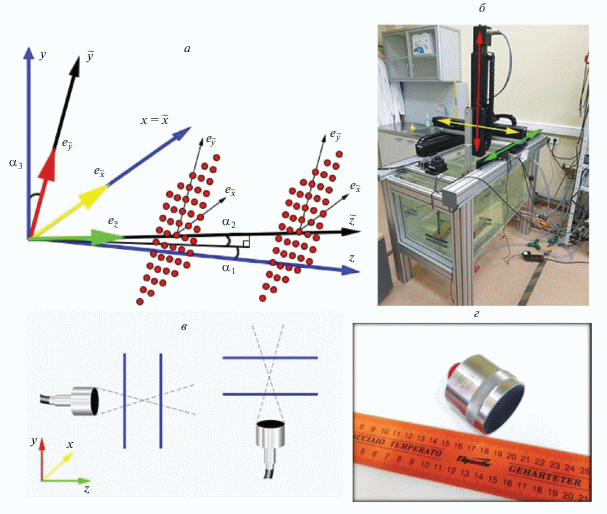
Рис. 1.
Ортогональная (синие оси) и неортогональная (черные оси) СК. Красными точками показаны координаты, в которых происходит запись сигнала на двух голограммах в неортогональной СК. Углы ${{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},{{{{\alpha }}}_{3}}$ описывают неортогональную СК относительно ортогональной СК, ${{\alpha }_{1}} = \angle \left( {y\tilde {z},~yz} \right),$ ${{\alpha }_{2}} = \angle \left( {x\tilde {z},~xz} \right),$ ${{\alpha }_{3}} = \angle \left( {\tilde {y},y} \right)$ (а). Система позиционирования (б). Схема измерений; две голограммы измерены параллельно плоскости $\left( {x,y} \right),$ две другие – параллельно плоскости $\left( {x,z} \right)$ (в). Акустический пьезопреобразователь, использованный в эксперименте (г).
Для демонстрации основных особенностей искажения результатов измерений из-за перекоса осей позиционера был проведен модельный эксперимент. Предполагалось, что в плоскости $\left( {x,y} \right)$ был расположен двумерный многоэлементный акустический преобразователь в виде квадратной решетки с количеством элементов $40 \times 40.$ Элементы имели квадратную форму размером ${{L}_{x}} = {{L}_{y}} = 1\,\,{\text{мм}}$ и были разделены зазорами шириной $d = 0.25\,\,{\text{мм}}.$ Амплитуда нормальной компоненты колебательной скорости в пределах каждого элемента предполагалась постоянной (поршневой источник). Излучение каждым элементом происходило в монохроматическом режиме на частоте ${{f}_{0}} = 2\,\,{\text{МГц}}$ с различной относительной фазой для обеспечения возможности электронной фокусировки акустического поля.
С помощью интеграла Рэлея [7] были рассчитаны двумерные распределения комплексной амплитуды акустического давления (голограмма) на плоском участке, параллельном поверхности излучателя, на расстоянии $z = H = 10\,\,{\text{мм}}$ от указанного излучателя. Расчет проводился для случаев отсутствия и наличия небольшого перекоса между осями, т.е. в точках, задаваемых координатами $\left( {x,y,~{\text{\;}}z = H} \right)$ и $\left( {\tilde {x},\tilde {y},~{\text{\;}}\tilde {z} = H} \right).$ Далее из полученных голограмм была рассчитана комплексная амплитуды акустического давления в пространстве перед двумерной решеткой; при этом расчет поля из голограммы, записанной в точках с координатами перекошенной СК, проводился в предположении, что соответствующие сигналы записаны в идеальной СК. Тем самым имитировалась ситуация, когда оператор измерительной системы использует позиционер с перекошенными осями, но не знает об этом (или знает, но пренебрегает этим) и поэтому при расчете поля из голограммы предполагает, что оси позиционера перпендикулярны.
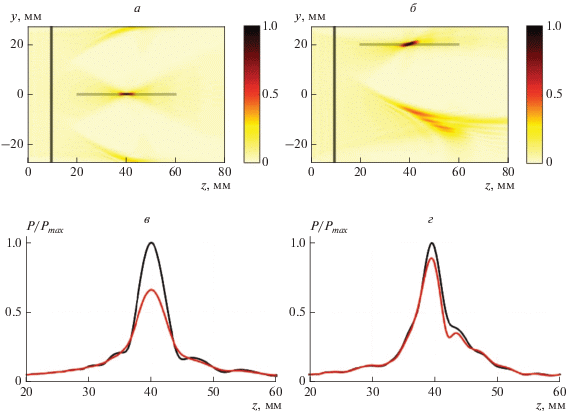
Рассматривался режим “электронной” фокусировки, при котором фазы сигналов на излучающих элементах решетки подбирались такими, чтобы излучаемое поле фокусировалось в заданную точку пространства (фокус). Описанный расчет был проведен для двух случаев электронной фокусировки: при фокусировке в точку с координатами $\left( {0,0,40\,\,{\text{мм}}} \right)$ и в точку $\left( {0,20,40\,\,{\text{мм}}} \right).$ Соответствующие нормированные распределения амплитуды поля акустического давления в плоскости $\left( {y,z} \right)$ показаны на рис. 2а, 2б. Для первого случая перекос осей был задан следующим: ${{{{\alpha }}}_{1}} = 1^\circ ,$ ${{{{\alpha }}}_{2}} = 1^\circ ,$ ${{{{\alpha }}}_{3}} = 0^\circ ,$ а для второго случая ${{{{\alpha }}}_{1}} = 0^\circ ,$ ${{{{\alpha }}}_{2}} = 0^\circ ,$ ${{{{\alpha }}}_{3}} = 1^\circ .$ На рис. 2в, 2г показаны амплитуды акустического давления, рассчитанные вдоль линий (указаны на рис. 2а, 2б) из искривленной и неискривленной голограмм. Наличие ненулевых углов ${{\alpha }_{1}}$ и ${{\alpha }_{2}}$ приводит к сдвигу всей структуры давления поперек оси $z,$ а ненулевой ${{\alpha }_{3}}$ заметным образом искажает пространственную структуру на удалении от оси $z.$ Таким образом, перекос осей системы позиционирования может существенно исказить результаты измерений и его необходимо учитывать.
Рис. 2.
Акустическое давление модельного многоэлементного излучателя при фокусировке в точку $\left( {0,~0,~40\,\,{\text{мм}}} \right)$ (а), $\left( {0,~20~\,\,{\text{мм}},~40\,\,{\text{мм}}} \right)~$ (б). Излучатель расположен в плоскости $\left( {x,y} \right)$ при $z = 0.$ Вертикальной линией показано положение голограммы, с которой проведен расчет, горизонтальной линией показана ось, распределение давления вдоль которой представлено на (в) и (г) соответственно, где черным цветом показаны профили давления при учете искривления осей СК, красным – без учета.
Для удобства теоретического описания введем орты перекошенной системы координат – сонаправленные с механическими осями системы позиционирования единичные векторы, которые обозначим ${{\vec {e}}_{{\tilde {x}}}},~{{\vec {e}}_{{\tilde {y}}}},{{\vec {e}}_{{\tilde {z}}}}.$ Все координаты будем задавать в неискаженной СК. Получим связь координат ортогональной (x, y, z) и неортогональной $\left( {\tilde {x},\tilde {y},\tilde {z}} \right)$ СК:
(1)
$\begin{gathered} {{{\vec {e}}}_{{\tilde {x}}}} = \left( {1,0,0} \right),\,\,\,\,{{{\vec {e}}}_{{\tilde {y}}}} = \left( {\sin {{{{\alpha }}}_{3}},\cos {{{{\alpha }}}_{3}},~0} \right), \\ {{{\vec {e}}}_{{\tilde {z}}}} = \left( {\sin {{{{\alpha }}}_{1}},\,\,\sin {{{{\alpha }}}_{2}},\,\,\sqrt {1 - {{{\sin }}^{2}}{\kern 1pt} {{{{\alpha }}}_{1}} - {{{\sin }}^{2}}{\kern 1pt} {{\alpha }_{2}}} } \right), \\ \end{gathered} $(2)
$\begin{gathered} x = \tilde {x} + \tilde {y}\sin {{{{\alpha }}}_{3}} + \tilde {z}\sin {{{{\alpha }}}_{1}};\,\,\,\,y = \tilde {y}\cos {{{{\alpha }}}_{3}} + \tilde {z}\sin {{{{\alpha }}}_{2}}; \\ z = \tilde {z}\sqrt {1 - {{{\sin }}^{2}}{\kern 1pt} {{{{\alpha }}}_{1}} - {{{\sin }}^{2}}{\kern 1pt} {{{{\alpha }}}_{2}}} . \\ \end{gathered} $Рассмотрим запись в виде углового спектра для решения уравнения Гельмгольца для спектральной амплитуды $P\left( {{{\omega }},\vec {r}} \right)$ акустического давления в произвольной точке декартовой системы координат [8]:
(3)
$\begin{gathered} P\left( {{{\omega }},x,y,z} \right) = {{\left( {\frac{1}{{2{{\pi }}}}} \right)}^{2}}\iint {{{S}_{0}}\left( {{{\omega }},{{k}_{x}},{{k}_{y}}} \right)} \times \\ \times \,\,{{e}^{{i{{k}_{x}}x + i{{k}_{y}}y + i\sqrt {{{k}^{2}} - k_{x}^{2} - k_{y}^{2}} ~z}}}d{{k}_{x}}d{{k}_{y}}, \\ \end{gathered} $(4)
$\begin{gathered} {\text{где}}\,\,\,{{S}_{0}}\left( {{{\omega }},{{k}_{x}},{{k}_{y}}} \right) = \\ = \,\,\iint {P\left( {{{\omega }},x,y,z = 0} \right)}{{e}^{{ - i{{k}_{x}}x - i{{k}_{y}}y}}}dxdy. \\ \end{gathered} $Представление волнового поля (3) имеет вид суперпозиции плоских волн вида ${{e}^{{i\vec {k}\vec {r}}}}.$ Волновой вектор в СК $\left( {x,y,z} \right)$ имеет вид $\vec {k} = ({{k}_{x}},{{k}_{y}},{\text{\;}}{{k}_{z}}$ = = $\sqrt {{{k}^{2}} - k_{x}^{2} - k_{y}^{2}} ),$ где волновое число $k = {{{\omega }} \mathord{\left/ {\vphantom {{{\omega }} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}.$ ${{S}_{0}}\left( {{{\omega }},{{k}_{x}},{{k}_{y}}} \right)$ – угловой спектр поля [9] в плоскости $z = 0$ на частоте ${{\omega }}{\text{.}}$ Рассчитаем его в искривленной СК, используя связь координат двух систем (2). Якобиан перехода в (4) от переменных $x,y$ к переменным $\tilde {x},\tilde {y}$ равен $\left| {\frac{{D\left( {x,y} \right)}}{{D\left( {\tilde {x},\tilde {y}} \right)}}} \right| = \cos {{{{\alpha }}}_{3}},$ поэтому
(5)
$\begin{gathered} {{S}_{0}}\left( {{{\omega }},{{k}_{x}},{{k}_{y}}} \right) = \cos {{{{\alpha }}}_{3}}\iint {P\left( {{{\omega }},\tilde {x},\tilde {y},\tilde {z} = 0} \right)} \times \\ \times \,\,{{e}^{{ - i{{k}_{x}}\tilde {x} - i\left( {{{k}_{y}}\cos {{{{\alpha }}}_{3}} + {{k}_{x}}\sin {{{{\alpha }}}_{3}}} \right)\tilde {y}}}}d\tilde {x}d\tilde {y} = \cos {{{{\alpha }}}_{3}}{{{\tilde {S}}}_{0}}\left( {\omega ,{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right), \\ \end{gathered} $(6)
${{\tilde {k}}_{x}} = {{k}_{x}};\,\,\,\,{{\tilde {k}}_{y}} = {{k}_{y}}\cos {{{{\alpha }}}_{3}} + {{k}_{x}}\sin {{{{\alpha }}}_{3}}.$С учетом (2), (3), (5) и $(6)$ получим решение уравнения Гельмгольца в искривленной системе координат. Якобиан перехода от переменных ${{k}_{x}},{{k}_{y}}$ к переменным ${{\tilde {k}}_{x}},{{\tilde {k}}_{y}}$ в данном случае равен $\left| {\frac{{D\left( {{{k}_{x}},{{k}_{y}}} \right)}}{{D\left( {{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)}}} \right| = \frac{1}{{\cos {{{{\alpha }}}_{3}}}}.$ Имеем:
(7)
$\begin{gathered} P\left( {{{\omega }},\tilde {x},\tilde {y},\tilde {z}} \right) = {{\left( {\frac{1}{{2{{\pi }}}}} \right)}^{2}}\iint {\widetilde {{{S}_{0}}}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right){{e}^{{i{{{\tilde {k}}}_{x}}\tilde {x} + i{{{\tilde {k}}}_{y}}\tilde {y}}}}} \times \\ \times \,\,\exp \left( {i\tilde {z}\left( {{{{\tilde {k}}}_{x}}\left( {\sin {{{{\alpha }}}_{1}} - {\text{tg}}{{{{\alpha }}}_{3}}\sin {{{{\alpha }}}_{2}}} \right) + \frac{{\sin {{{{\alpha }}}_{2}}}}{{\cos {{{{\alpha }}}_{3}}}}{{{\tilde {k}}}_{y}} + } \right.} \right. \\ \left. {\left. { + \,\,\sqrt {{{k}^{2}} - \tilde {k}_{x}^{2} - {{{\left( {\frac{{{{{\tilde {k}}}_{y}}}}{{\cos {{{{\alpha }}}_{3}}}} - {{{\tilde {k}}}_{x}}{\text{tg}}{{{{\alpha }}}_{3}}} \right)}}^{2}}} } \right)} \right)d{{{\tilde {k}}}_{x}}d{{{\tilde {k}}}_{y}} = \\ = {{\left( {\frac{1}{{2{{\pi }}}}} \right)}^{2}}\iint {{{{\tilde {S}}}_{{{{Z}_{0}}}}}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)\,}{{e}^{{i{{{\tilde {k}}}_{x}}\tilde {x} + i{{{\tilde {k}}}_{y}}\tilde {y}}}}d{{{\tilde {k}}}_{x}}d{{{\tilde {k}}}_{y}}. \\ \end{gathered} $Таким образом, отношение угловых спектров, измеренных в искривленной СК на плоскости $\tilde {z} = {{Z}_{0}}$ и на параллельной плоскости $\tilde {z} = 0,$ имеет следующий вид
(8)
$\begin{gathered} {\text{П}}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right) = \frac{{{{{\tilde {S}}}_{{{{Z}_{0}}~}}}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)}}{{{{{\tilde {S}}}_{0}}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)}} = \\ = \exp \left[ { - i\left( {{{{\tilde {k}}}_{x}}{{x}_{0}} + {{{\tilde {k}}}_{y}}{{y}_{0}}} \right) + i{{Z}_{0}}\sqrt {1 - {{{\sin }}^{2}}{\kern 1pt} {{{{\alpha }}}_{1}} - {{{\sin }}^{2}}{\kern 1pt} {{{{\alpha }}}_{3}}} \times _{{_{{_{{_{{_{{}}}}}}^{{}}}}^{{}}}}^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}} \right. \\ \times \,\,\left. {\sqrt {{{k}^{2}} - \tilde {k}_{x}^{2} - {{{\left( {\frac{{{{{\tilde {k}}}_{y}}}}{{\cos {{{{\alpha }}}_{3}}}} - {{{\tilde {k}}}_{x}}{\text{tg}}{{{{\alpha }}}_{3}}} \right)}}^{2}}} } \right] = \\ = \exp \left( {i{{\Phi }}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)} \right), \\ \end{gathered} $(9)
$\begin{gathered} {\text{где}}\,\,\,\,{{x}_{0}} = - \left( {\sin {{{{\alpha }}}_{1}} - {\text{tg}}{\kern 1pt} {{{{\alpha }}}_{3}}\sin {{{{\alpha }}}_{2}}} \right){{Z}_{0}}; \\ {{y}_{0}} = - \frac{{\sin {{{{\alpha }}}_{2}}}}{{\cos {{{{\alpha }}}_{3}}}}{{Z}_{0}}. \\ \end{gathered} $Указанная функция ${\text{П}}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)$ может быть названа пропагатором. Значения ${{x}_{0}},{{y}_{0}}$ соответствуют величине поперечного смещения точки на оси $\tilde {z}$ на расстоянии Z0 относительно ортогональной СК. Отметим, что функция ${{\Phi }}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)$ при фиксированной частоте $\omega $ представляет собой семейство эллипсоидальных замкнутых кривых и не зависит от геометрии используемого преобразователя и его расположения относительно плоскостей голограмм. Следовательно, в измерениях по определению перекоса осей системы позиционирования можно выбирать преобразователь из соображений удобства, необходимого времени измерений и т.д. Тем не менее, следует заметить, что определение фазовой функции ${{\Phi }}$ возможно в таких областях $\left( {{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right),$ где амплитуды измеренных угловых спектров $\left| {{{{\tilde {S}}}_{0}}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)} \right|$ и $\left| {{{{\tilde {S}}}_{{{{Z}_{0}}}}}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)} \right|$ заметно отличны от нуля. Этот факт следует учитывать при выборе источника УЗ поля.
Таким образом, измерив две голограммы на разных расстояниях от преобразователя, можно получить функцию, зависящую от двух аргументов ${{k}_{x}},{{k}_{y}}$ и трех параметров ${{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},{{{{\alpha }}}_{3}}.$ Далее, сравнивая экспериментальный и теоретический пропагаторы, можно рассчитать углы, определяющие неортогональную СК и, следовательно, количественно определить неортогональность самой системы позиционирования, на которой было выполнено измерение.
ЭКСПЕРИМЕНТ
В работе измерялся перекос механических осей системы позиционирования UMS-3 (Precision Acoustics, Великобритания) (рис. 1б). Перекос вносился искусственно, чтобы иметь возможность исследовать разные углы перекоса. Проведены три серии измерений, в каждой из которых ось $\tilde {y}$ была отклонена от оси $y$ на различный угол ${{{{\alpha }}}_{3}}.$ В измерениях использован акустический пьезопреобразователь (рис. 1г) с диаметром $D = 38.1\,\,{\text{мм}},$ фокусным расстоянием $F = 63.5\,\,{\text{мм}}$ и рабочей частотой 1 МГц (V392, Panametrics, США). Излучатель погружался в резервуар с дегазированной водой и с точностью порядка градуса располагался параллельно плоскости голограммы, что достигалось путем его предварительного выравнивания относительно механических осей системы позиционирования на поворотной крепежной платформе. Как было отмечено выше, функция ${{\Phi }}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)$ в выражении (8) не зависит от взаимного расположения излучателя относительно голограммы, поэтому точность установки излучателя в рамках предлагаемого подхода не играет значимой роли. При этом важно, чтобы при измерениях исходное положение не изменялось, что достигалось жестким закреплением источника. Указанное выравнивание излучателя проводилось для того, чтобы в область голограммы, которая обычно располагается почти перпендикулярно акустической оси источника [10], попадала максимально возможная для данной геометрии энергия акустического пучка, что позволяет получить наибольшее отношение сигнал/шум в точках голограммы.
В одной серии измерений с заданным углом ${{{{\alpha }}}_{3}}$ были записаны четыре голограммы: две из них были расположены параллельно плоскости $\left( {x,y} \right)$ при горизонтальном расположении оси источника (рис. 1в), две – параллельно плоскости $\left( {x,\tilde {z}} \right)$ при вертикальном расположении оси. Одна голограмма была измерена на расстоянии 1.5 см до фокуса, другая – за фокусом на таком же расстоянии. С помощью генератора (33250A, Agilent, США) на излучатель подавалось напряжение в виде радиоимпульса с прямоугольной огибающей с амплитудой $U = 5\,\,{\text{В,}}$ состоявшего из трех периодов синусоидального сигнала частоты ${{f}_{0}} = 1\,\,{\text{МГц}}{\text{.}}$ Использовался период повторения $T = 4\,\,{\text{мс}}{\text{.}}$ Все голограммы измерялись идентично и имели одинаковые характеристики: размер $201\,\, \times \,\,201$ точек, шаг $dx = dy = 0.5\,\,{\text{мм}}{\text{.}}$ В каждой точке временной профиль сигнала записывался с помощью гидрофона (HNA-0400, Onda, США) и осциллографа (TDS5034B, Tektronix, США), количество усреднений в каждой точке составляло ${{N}_{{a{v}}}} = 48,$ время усреднения ${{T}_{{a{v}}}} = 400\,\,{\text{мс}}{\text{.}}$ Длительность временного окна составляла $T = 100\,\,{\text{мкс}},$ что обеспечивало запись информативной части сигнала, шаг дискретизации $dt = 20\,\,{\text{нс}}$ обеспечивал необходимую ширину частотного окна.
В результате расчета время-частотного спектра сигнала во всех пространственных точках голограмм были получены пространственные распределения амплитуд и фаз для всех спектральных компонент, т.е. набор монохроматических голограмм поля. В работе применялся широкополосный преобразователь, что позволило использовать большой набор монохроматических голограмм для повышения точности определения углов перекоса осей. Ближняя к излучателю голограмма в виде нормированной амплитуды и фазы акустического давления на частоте $f = 1\,\,{\text{МГц}},$ показана на рис. 3а, 3г соответственно. Исходя из значений спектральной плотности сигнала в опорных точках голограммы, например, в центре, можно определить частотный диапазон, в котором будет проводится определение функции ${{\Phi }}\left( {{{\omega }},{{{\tilde {k}}}_{x}},{{{\tilde {k}}}_{y}}} \right)$ (8). Этот диапазон, в первую очередь, обусловлен полосой излучаемого преобразователем сигнала. В настоящей работе он был выбран в пределах $f \in \left( {0.4,{\text{\;}}1.6} \right)\,\,{\text{МГц}},$ что с шагом по частоте $df = 10\,\,{\text{кГц}}$ составило ${{N}_{f}} = 121$ спектральную компоненту.
Рис. 3.
Нормированная амплитуда (а) и фаза (г) ближней к преобразователю монохроматической голограммы акустического давления на частоте $f = 1\,\,{\text{МГц}}.$ Модуль (б) и фаза (д) углового спектра той же монохроматической голограммы. Фаза отношения дальней и ближней к преобразователю угловых спектров, полученных из эксперимента (в). Фаза теоретического отношения угловых спектров (8) при нулевых углах ${{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{3}}$ (е). Пунктирной линией обозначается область радиуса ${{k}_{0}},$ в которой проводился поиск углов по формуле (10).
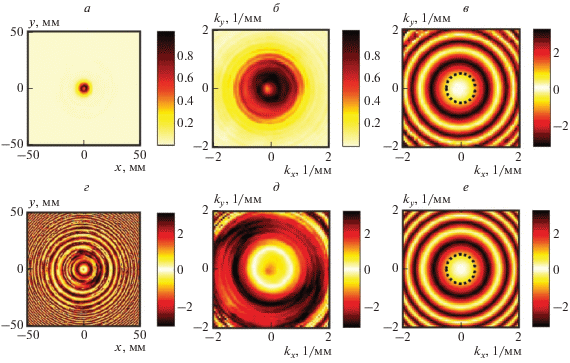
Из полученных дальней и ближней монохроматических голограмм были рассчитаны соответствующие угловые спектры сигнала по формуле (4). Модуль углового спектра для ближней к излучателю голограммы представлен на рис. 3б, фаза – на рис. 3д. После этого было найдено поточечное отношение угловых спектров, фаза которого для частоты 1 МГц показана на рис. 3в. Дополнительно на рис. 3е показана фаза теоретического отношения угловых спектров (8) при нулевых углах ${{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},{{{{\alpha }}}_{3}}.$ Стоит еще раз отметить, что проводить измерения ближней и дальней голограмм следует при одном и том же положении излучателя, изменение его положения между измерениями дальней и ближней голограмм внесет дополнительную ошибку в определяемые углы.
Углы ${{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},{{{{\alpha }}}_{3}}$ были определены путем минимизации разницы экспериментальной и теоретической фазы пропагатора. Углы в формуле (8) для ${{\Phi }}\left( {{{k}_{x}},{{k}_{y}}} \right)$ варьировались вокруг нулевого значения, и определялись углы, при которых сумма квадратов поэлементной разницы экспериментальной и теоретической фаз пропагатора в заданной круговой области была минимальна:
(10)
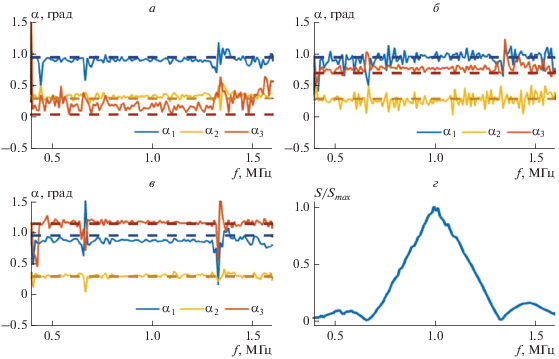
$\mathop {\min }\limits_{{{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},{{{{\alpha }}}_{3}}} \sum\limits_{k_{x}^{2} + k_{y}^{2} < k_{0}^{2}} {{{{\left( {{{{\text{П}}}_{E}}\left( {{{\omega }},{{k}_{x}},{{k}_{y}}} \right) - {{{\text{П}}}_{T}}\left( {{{\omega }},{{k}_{x}},{{k}_{y}}} \right)} \right)}}^{2}}} .$Радиус круга ${{k}_{0}},$ в котором происходит расчет по формуле (10), определялся таким образом, чтобы дисперсии значений определяемых углов по частоте (рис. 4а–4в) были минимальны. При меньших значениях ${{k}_{0}}$ бо́льшая дисперсия вызвана малым количеством пространственных частот, которые используются для поиска углов, при больших значениях ${{k}_{0}}$ бо́льшая дисперсия вызвана включением в расчет угловых компонент с низкой спектральной плотностью, которые являются источником значительных случайных отклонений. В представленном на рис. 4 случае значение ${{k}_{0}}$ было выбрано таким образом, что количество угловых компонент, попадающих в окружность радиусом ${{k}_{0}},$ равнялось $N = 225.$
Рис. 4.
Углы ${{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{3}},$ полученные из голограмм на разных частотах в трех сериях измерений: без дополнительного перекоса (а), дополнительный перекос оси ${{\Delta }}{{\alpha }_{3}} \approx 0.8^\circ $ (б), дополнительный перекос ${{\Delta }}{{\alpha }_{3}} \approx 1.1^\circ $ (в). Пунктирными линиями показаны углы, измеренные геометрическим методом с использованием лазерной системы. Спектр акустического сигнала в центре ближней голограммы (г).
Указанная операция проводилась для монохроматических голограмм на разных частотах. В формуле (8), в отличие от ${{{{\alpha }}}_{1}},{{{{\alpha }}}_{2}},$ зависимость от параметра ${{{{\alpha }}}_{3}}$ является слабой, и по экспериментальным голограммам, записанным вдоль (x, y) на разных расстояниях z, точное определение ${{{{\alpha }}}_{3}}$ является затруднительным. Чтобы с сопоставимой точностью найти все три угла, которые характеризуют неортогональную (реальную) СК, следует объединить измерения при разных ориентациях голограммы и излучателя относительно системы позиционирования (рис. 1в). Имея два наиболее точно определенных угла ${{\alpha }_{1}}$ и ${{\alpha }_{2}},$ задающих поперечную голограмме ось при ориентации голограммы параллельно плоскости $\left( {x,\tilde {y}} \right),$ и углы ${{\alpha }}_{1}^{{\text{'}}}$ и ${{\alpha }}_{2}^{{\text{'}}}$ при расположении голограммы параллельно плоскости $\left( {x,\tilde {z}} \right),$ можно определить угол ${{\alpha }_{3}}$ по следующей формуле в приближении малых углов:
(11)
${{{{\alpha }}}_{3}} = \arcsin \sqrt {{{{\sin }}^{2}}{\kern 1pt} {{\alpha }}_{1}^{{\text{'}}} + {{{\sin }}^{2}}{\kern 1pt} {{\alpha }}_{2}^{{\text{'}}} - {{{\sin }}^{2}}{\kern 1pt} {{{{\alpha }}}_{2}}} .$На рис. 4 показана полученная частотная зависимость трех углов для трех серий измерений. Можно заметить, что в окрестности частот $f = 0.67{\text{--}}1.32\,\,{\text{МГц}}$ отклонение значений углов от своих средних значений существенно выше, чем в остальной области. Это связано с тем, что спектральная мощность сигнала (рис. 4г) на этих частотах мала из-за выбранной формы подаваемого импульса и особенностей преобразователя. Значения углов на разных частотах можно считать определенными независимо, поэтому, усредняя их в оптимальном диапазоне частот, можно минимизировать случайные отклонения и получить значения углов с высокой точностью. В табл. 1 приведены значения трех углов со среднеквадратичным отклонением для трех серий измерений.
Таблица 1.
Углы перекоса осей системы позиционирования, полученные в трех сериях измерений и измеренные геометрическим методом
| ${{\alpha }_{1}}$, град | ${{\alpha }_{2}}$, град | ${{\alpha }_{3}}$, град | |
|---|---|---|---|
| Нет дополнительного перекоса | 0.91 ± 0.03 | 0.33 ± 0.03 | 0.17 ± 0.06 |
| Перекос ${{\Delta }}{{\alpha }_{3}} \approx 0.8^\circ $ | 0.96 ± 0.08 | 0.26 ± 0.09 | 0.78 ± 0.03 |
| Перекос ${{\Delta }}{{\alpha }_{3}} \approx 1.1^\circ $ | 0.87 ± 0.02 | 0.31 ± 0.02 | 1.16 ± 0.02 |
| Геометрические измерения с использованием лазера | 0.95 ± 0.2 | 0.3 ± 0.2 | 0.04 ± 0.2 |
| 0.95 ± 0.2 | 0.3 ± 0.2 | 0.7 ± 0.2 | |
| 0.95 ± 0.2 | 0.3 ± 0.2 | 1.14 ± 0.2 |
Рабочий ход вдоль осей использованной в работе системы позиционирования достаточно протяженный (${{\Delta }}L_{{max}}^{x} = 0.3\,\,{\text{м}},$ ${{\Delta }}L_{{max}}^{y} = 0.3\,\,{\text{м}},$ ${{\Delta }}L_{{max}}^{z} = 0.4\,\,{\text{м}}$), поэтому можно измерить углы перекоса оптическим методом. Для этого на системе позиционирования закреплялся лазерный источник, и в крайних положениях по каждой из осей отмечались проекции лазерного луча на прозрачные стенки водяного резервуара. Далее был определен угол между прямыми, соединяющими противоположные точки, лежащие на одной оси. На рис. 4 пунктирными линиями показаны результаты таких измерений. Они хорошо согласуются с результатами расчета из голограмм табл. 1. Погрешность определения углов оптическим способом определялась размером проекции лазерного пятна и расстоянием между крайними точками, что для описываемого случая составило величину ${{\Delta }}\alpha = 0.2^\circ .$ Для систем позиционирования с меньшим диапазоном линейных перемещений данная ошибка будет значительнее.
ЗАКЛЮЧЕНИЕ
В работе исследовано влияние неортогональности осей системы позиционирования на точность пространственной характеризации акустического поля. Описан и экспериментально проверен новый способ определения отклонения осей системы позиционирования от ортогональности. Результаты эксперимента и моделирования показывают, что для достоверного определения трех углов неортогональной системы координат необходимо провести измерения при разных ориентациях голограммы и излучателя относительно системы позиционирования. Определенные таким методом углы обладают меньшей погрешностью по сравнению с геометрическим методом измерения в условиях имеющейся системы. Используя полученные данные можно легко скорректировать измеренные на данной системе позиционирования голограммы излучателей. Также следует отметить, что имеется возможность усовершенствовать данную методику, уменьшив количество измерений, для чего следует проводить измерение голограмм в плоскостях, которые не параллельны плоскостям, образованными осями системы позиционирования.
Работа выполнена при поддержке РФФИ (проекты № 19-32-90022, 18-02-00991).
Список литературы
Субботин В.Г., Сапожников О.А., Цысарь С.А. // Сб. тр. XXV сессии Росс. акуст. общ. 2012. Т. 2. С. 123.
Sapozhnikov O.A., Tsysar S.A., Khokhlova V.A. et al. // JASA. 2015. V. 138. No. 3. P. 1515.
Kreider W., Khokhlova V., Tsysar S. et al. // JASA. 2017. V. 141. No. 5. P. 4009.
Pye S.D. // Physiotherapy. 1996. V. 82. No. 1. P. 39.
Сухоручкин Д.А., Юлдашев П.В., Цысарь С.А. и др. // Изв. РАН. Сер. физ. 2018. Т. 82. № 5. С. 578; Sukhoruchkin D.A., Yuldashev P.V., Tsysar S.A. et al. Bull. Russ. Acad. Sci. Phys. 2018. V. 82. No. 5. P. 507.
Nikolaev D., Tsysar S. Krendeleva A. et al. // POMA. 2019. V. 38. No. 045012. P. 1.
Cathignol D., Sapozhnikov O.A. // Acoust. Phys. 1999. V. 45. No. 6. P. 735.
Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука, 1979. 384 с.
Schafer M.E., Lewin P.A. // JASA. 1989. V. 85. No. 5. P. 2202.
Marhenke T., Sanabria S.J., Chintada B.R. et al. // Sensors. 2019. V. 19. P. 863.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


