Известия РАН. Серия физическая, 2021, T. 85, № 7, стр. 948-952
Построение парных потенциалов Морзе для никеля и кобальта на основе уточнения значений параметра Грюнайзена и атомной сжимаемости
М. Ю. Семенов 1, *, И. П. Королев 1, В. Арестов 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный технический университет имени Н.Э. Баумана
(национальный исследовательский университет)”
Москва, Россия
* E-mail: Semenov.m.yu@bmstu.ru
Поступила в редакцию 25.01.2021
После доработки 25.02.2021
Принята к публикации 29.03.2021
Аннотация
Для атомистических расчетов фазовых превращений разработаны парные потенциалы Морзе никеля и кобальта. Для построения парных потенциалов использованы значения равновесных межатомных расстояний, а также энергий сублимации. Построены парные потенциалы, адекватные значениям объемного модуля упругости при различных температурах, при значениях параметра Грюнайзена никеля приблизительно равным 1.72 для никеля и 1.85 для кобальта.
ВВЕДЕНИЕ
Несмотря на то, что некоторыми исследователями разрабатываются парные потенциалы вида Ми-Леннарда-Джонса (например, для золота и ряда переходных металлов с решеткой ОЦК [1]), согласно [2] именно парный потенциал в форме Морзе в наибольшей мере отражает физическую природу межатомных взаимодействийв переходных металлах и их сплавах.
Парные потенциалы Морзе использовали для оценки энергетического порога полиморфного превращения железа из феррита в аустенит [3]. Элементарный акт фазового превращения был ранее атомистически рассмотрен как двумерное преобразование в кластере, состоящем из четырех атомов железа, согласно которому превращение заключается в переброске диагонали ромба, составленного из двух треугольников. В вершинах треугольников расположены атомы металла, а при полиморфном превращении перебрасывается общее ребро (становится из короткой диагонали длинной диагональю ромба). В момент преодоления энергетического порога превращения ромб становится квадратом, а диагонали, соответственно, равными. Значение энергетического порога может быть рассчитано при помощи парных потенциалов по изменению межатомных расстояний.
Численные параметры функции, аппроксимирующей парный потенциал в форме Морзе [4], были калиброваны по экспериментальным значениям энергий сублимации и температурным зависимостям упругих констант железа. В результате атомистических расчетов при помощи потенциала Морзе получили значение энергетического порога превращения аустенита в феррит при температуре 1184 К, равное 162.1 кДж ∙ моль–1 [5]. Эта численная оценка близка к экспериментальному определению энтальпии активации превращения феррита в аустенит, которая равна 166.4 кДж ∙ моль–1 [6].
Такой подход применили к оценке энергетического порога полиморфного превращения в чистом железе, хроме, марганце, а также сплавах систем Fe–Cr и Fe–Mn [3]. При разработке парных потенциалов в форме Морзе использовали значения атомной сжимаемости железа, хрома и марганца из работы [7]. Адекватность парных потенциалов подтверждается удовлетворительным совпадением температурных зависимостей объемного модуля упругости, полученных расчетным путем из парного потенциала, с известными экспериментальными зависимостями. При этом, согласно выполненным расчетам, значение энергетического порога превращения феррит-аустенит в системе Fe–Cr составило 196 кДж ∙ моль–1, что удовлетворительно соотносится со значением энергии соответствующего превращения в низкоуглеродистой стали 005Х9, экспериментально определенным как 199–212 кДж ∙ моль–1 [8].
Целью настоящей работы явилось построение адекватных парных потенциалов никеля и кобальта, необходимых для выполнения атомистических расчетов атомных кластеров в системах Fe–Ni, Fe–Co, Ni–Cr, Ni–Co и других для изучения фазовых превращений, а также диффузионных процессов в сплавах указанных систем легирования.
МЕТОДИКА РАЗРАБОТКИ ПАРНЫХ ПОТЕНЦИАЛОВ И ПРОВЕРКА ИХ АДЕКВАТНОСТИ
В [3, 5], применяли выражение парного потенциала Морзе в виде [2]:
(1)
$U = {{U}_{b}} + {{U}_{r}} = - \alpha \exp \left( { - \frac{{\lambda d}}{2}} \right) + \beta \exp \left( { - \lambda d} \right),$Минимум межатомного потенциала U = U0 при равновесном межатомном расстоянии d = d0 = 2r0 равен энергии сублимации металла:
Температурная зависимость энергии сублимации представляет собой сумму:
где Hs – энтальпия сублимации; Ss – энтропия сублимации при 450–1250 К; T – температура.Энтальпию сублимации никеля при комнатной температуре приняли равной 421 кДж ∙ моль–1 [9], кобальта – 389 кДж ∙ моль–1 [10].
Величину Ss определяли аналогично энтропии активации диффузии по формуле [11, 12]:
где G – модуль сдвига; G0 – модуль сдвига при T = 0 К.Калибровку энергии сублимации проводили при помощи формулы (4) по температурной зависимости модуля сдвига:
где ζ – коэффициент пропорциональности, который находили путем регрессионного анализа экспериментальных данных.В результате регрессионного анализа экспериментальных данных из работы [13], выражение (5) для никеля приобрело вид:
Используя данные [14] для кобальта выражение (5) преобразовали в:
Проверку адекватности выражения парного потенциала выполняли путем сравнения с экспериментальными данными расчетного значения объемного модуля упругости при равновесном межатомном расстоянии:
(8)
$B\left( {d = {{d}_{0}}} \right) = \Omega \frac{{{{\partial }^{2}}U}}{{\partial {{\Omega }^{2}}}},$Рассчитанное на основе парного потенциала (1) значение объемного модуля упругости никеля при температурах 500–1000°C превосходит экспериментальные значения почти вдвое. Также к неудовлетворительным результатам приводит парный потенциал (1) для кобальта (расчетное и эмпирическое значения объемного модуля упругости при 700°C соотносятся как 272 и 171 ГПа, соответственно). Отклонение от экспериментальных данных возрастает при применении потенциала Ми–Леннарда-Джонса.
В этой связи приняли парный потенциал Морзе в форме:
(9)
$\begin{gathered} U = {{U}_{b}} + {{U}_{r}} = {{U}_{s}} \times \\ \times \,\,\left\{ {\exp \left[ { - 2{{\varphi }}\left( {\frac{d}{{{{d}_{0}}}} - 1} \right)} \right] - 2\exp \left[ { - {{\varphi }}\left( {\frac{d}{{{{d}_{0}}}} - 1} \right)} \right]} \right\}, \\ \end{gathered} $Равновесное межатомное расстояние d0 в никеле и кобальте принято равным 0.248 и 0.250 нм, соответственно.
Значения параметра Грюнайзена для выражения (9) подбирали итерационным методом таким образом, чтобы обеспечить максимальную сходимость расчетных и экспериментальных значений объемного модуля упругости. Получили для никеля γ = 1.72 ± 0.05, а для кобальта γ = 1.85 ± 0.05.
Расхождение между расчётными экспериментальными значениями объемного модуля упругости Ni и Co при 500–900°C минимально (табл. 1). Таким образом достигнута удовлетворительная адекватность парного потенциала (9) для никеля и кобальта.
Таблица 1.
Расчетные и экспериментальные значения объемного модуля упругости никеля и кобальта при 500–900°С
| Температура, °С | Объемный модуль упругости, ГПа | |||
|---|---|---|---|---|
| никель | кобальт | |||
| расчет | эксперимент | расчет | эксперимент | |
| 500 | 185 | 183 | 184 | 186 |
| 700 | 173 | 171 | 169 | 171 |
| 900 | 162 | 160 | 154 | 156 |
Полученные при помощи выражения (9) значения энергий взаимного притяжения и отталкивания атомов легирующих элементов, а также железа [3] использовали для решения асимметричной задачи, т.е. расчета энергий взаимного притяжения и отталкивания пары атомов Fe и X (Ni или Co) ($U_{b}^{{{\text{Fe}}--{\text{X}}}}(d)$ и $U_{r}^{{{\text{Fe}}--{\text{X}}}}(d),$ соответственно) при произвольном межатомном расстоянии dсогласно выражению [2]:
(10)
$U_{b}^{{{\text{Fe}} - {\text{X}}}}\left( d \right) = - {{W}^{{{\text{Fe}} - {\text{X}}}}}\left( d \right)N_{{\text{d}}}^{{{\text{Fe}} - {\text{X}}}}{{\left( {10 - N_{{\text{d}}}^{{{\text{Fe}} - {\text{X}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {10 - N_{{\text{d}}}^{{{\text{Fe}} - {\text{X}}}}} \right)} {20}}} \right. \kern-0em} {20}},$(11)
${{W}^{{{\text{Fe}} - {\text{X}}}}}\left( d \right) = {{\left\{ {0.5\left[ {{{W}^{{{\text{Fe}}}}}{{{\left( d \right)}}^{2}} + {{W}^{{\text{X}}}}{{{\left( d \right)}}^{2}}} \right]} \right\}}^{{0.5}}},$(12)
${{W}^{{{\text{Me}}}}}\left( d \right) = \frac{{20}}{{{{N}_{d}}}}U_{b}^{{{\text{Me}}}}\left( d \right)\left( {1 - {{N}_{d}}} \right),$(13)
$U_{r}^{{{\text{Fe}} - {\text{X}}}}\left( d \right) = {{W}^{{{\text{Fe}} - {\text{X}}}}}\left( d \right)N_{d}^{{{\text{Fe}} - {\text{X}}}}{{\left( {10 - N_{d}^{{{\text{Fe}} - {\text{X}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {10 - N_{d}^{{{\text{Fe}} - {\text{X}}}}} \right)} {40}}} \right. \kern-0em} {40}},$Тогда межатомный потенциал кластера железо – легирующий элемент при межатомном расстоянии d может быть определен по уравнению [2]:
РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ
Определенное в настоящей работе значение параметра Грюнайзена Ni (1.72) сопоставили с литературными данными, в соответствии с которыми γ никеля принимает значения от 1.3 до 1.9. Так, согласно [15] параметр Грюнайзена Ni равен 1.3; согласно [16] – 1.73; согласно [17] – 1.87. Значение параметра Грюнайзена Co по нашим данным (1.85) заметно отличается от данных [17], согласно которым γ кобальта равен 2.15. В [18] параметр Грюнайзена определяли экспериментально по акустическим данным, при этом γ никеля определили как 1.70; а γ кобальта – как 1.85.
Таким образом, полученное нами значение параметра Грюнайзена никеля, в целом, находится в удовлетворительном согласии с литературными данными. Определенное в настоящей работе значение параметра Грюнайзена кобальта существенно уточняет данные [17], при этом совпадает с результатами анализа акустических данных, представленными в [18]. Найденным значениям параметра Грюнайзена соответствуют значения атомной сжимаемости из выражения (1) никеля λ = 2.78 Å–1 и кобальта λ = 2.96 Å–1, которые существенно отличаются от предложенных Петтифором в [7].
Расчетные и экспериментальные температурные зависимости объемного модуля упругости в системах Fe–Ni и Fe–Co, установленные при помощи парных потенциалов железа [3], а также никеля, кобальта и асимметричных потенциалов атомов Fe и Ni, Fe и Co, полученных в настоящей работе, показывают наличие наиболее сильной химической связи между атомами железа и никеля (рис. 1), а также железа и кобальта (рис. 2) по сравнению со связями между атомами одного сорта (Fe, Ni, Co).
Рис. 1.
Расчетные(сплошные) и экспериментальные (пунктирные) температурные зависимости объемного модуля упругости в системе железо–никель.
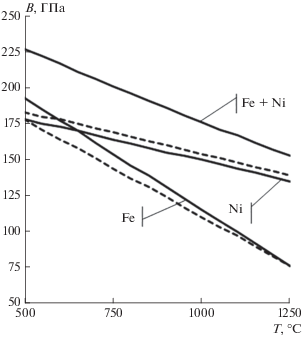
Рис. 2.
Расчетные(сплошные) и экспериментальные (пунктирные) температурные зависимости объемного модуля упругости в системе железо–кобальт.
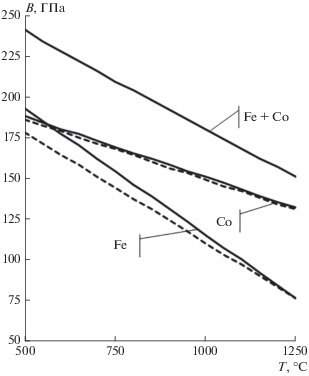
Расчетное и экспериментальное значение объемного модуля упругости в системе железо-никель при 1000°С составляет около 175 ГПа (см. рис. 1). Для сравнения объемный модуль упругости в системе железо–хром при 1000°С составляет менее 150 ГПа [3], что указывает на значительно меньшую энергию связи. Действительно, как показывает анализ выражений коэффициента диффузии хрома и никеля в аустените [19], коэффициент диффузии хрома в ГЦК железе при 1000°С почти в 5 раз выше, чем никеля.
ЗАКЛЮЧЕНИЕ
На основе анализа температурных зависимостей объемного модуля упругости и парного потенциала Морзе уточнены значения параметра Грюнайзена никеля и кобальта, которые равны 1.72 ± 0.05 и 1.85 ± 0.05, соответственно. При этом, они удовлетворительно соотносятся с результатами других исследователей. Определены значения атомной сжимаемости для никеля и для кобальта, равные 2.78 и 2.96 Å–1, соответственно, обеспечивающие при их применении в парных потенциалах Морзе хорошее совпадение с экспериментальными температурными зависимостями упругих констант. Разработаны ассиметричные парные потенциалы для атомов железа и никеля, а также железа и кобальта, которые показывают сильную химическую связь между атомами Fe и Ni, а также Fe и Co, которая обуславливает заметно более низкое значение коэффициента диффузии никеля в железе по сравнению коэффициентом диффузии хрома в железе (меньшее в 5 раз при температуре 1000°C). Полученные парные потенциалы могут быть использованы при атомистических расчетах фазовых превращений, а также элементарных актов диффузии легирующих элементов замещения в сплавах на базе железа и никеля.
Список литературы
Магомедов М.Н. // ФТТ. 2020. Т. 62. № 7. С. 998; Magomedov M.N. // Phys. Sol. St. 2020. V. 62. No. 7. P. 1126.
Pettifor D.G. Bonding and structure of molecules and solids. Oxford, 1996. 296 p.
Семенов М.Ю., Крапошин В.С., Талис А.Л., Симич-Лафицкий Н.Д. // МиТОМ. 2020. № 2. С. 776. С. 8; Semenov M.Yu., Kraposhin V.S., Talis A.L., Simich-Lafitskii N.D. // Met. Sci. Heat Treat. 2020. V. 62. Nos. 1–2. P. 109.
Morse P.M. // Phys. Rev. 1929. V. 34. No. 1. P. 57.
Kraposhin V.S., Simich-Lafitskiy N.D., Talis A.L. et al. // Acta Cryst. B. 2019. V. B75. P. 325.
Caballero F.G., Capdevila C., García de Andrés C. // Mater. Sci. Technol. 2001. V. 17. P. 1114.
Pettifor D.G. In: Physical metallurgy. V. 1. Amsterdam, Lausanne, N.Y., Oxford, Shannon, Tokyo, North-Holland, 1996. P. 47.
Мирзаев Д.А., Окишев К.Ю., Счастливцев В.М. и др. // Изв. ЧНЦ. 1998. № 2. С. 27.
Kant A. // Chem. Phys. 1964. V. 41. No. 6. P. 1872.
Kant A., Strauss B. // Chem. Phys. 1964. V. 41. No. 12. P. 3806.
Zener C. // J. Appl. Phys. 1951. V. 22. No. 4. P. 372.
Christian J.W. The theory of transformations in metals and alloys. Amsterdam, Boston, London, N.Y., Oxford, Paris, 2002.
Ledbetter H.M., Reed R.P. // J. Phys. Chem. Ref. Data. 1973. V. 2. No. 3. P. 531.
Nadal M.H., Hubert C., Oltra R. // J. Appl. Phys. 2009. V. 106. No. 2. Art. No. 024906.
Wang X., Nie S., Li J. et al. // Appl. Phys. Lett. 2008. V. 92. No. 12. Art. No. 121918.
Urzendowski R., Guenther A.H. // AIP Conf. Proc. 1974. V. 17. No. 1. P. 256.
White G.K. // Proc. Phys. Soc. 1965. V. 86. No. 1. P. 159.
Беломестных В.Н. // Письма ЖТФ. 2004. Т. 30. № 3. С. 14; Belomestnykh V.N. // Tech. Phys. Lett. 2004. V. 30. No. 2. P. 91.
Le Claire A.D., Neumann G. In: Diffusion in solid metals and alloys. Berlin, Heidelberg, 1990. P. 85.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


