Известия РАН. Серия физическая, 2021, T. 85, № 8, стр. 1137-1141

Спиновый обмен как пример обмена тождественных квантовых объектов

Г. Е. Карнаух^*

Федеральное государственное бюджетное учреждение науки Институт проблем химической физики Российской академии наук
Черноголовка, Россия

^* E-mail: karnaukh@icp.ac.ru

Поступила в редакцию 12.03.2021
После доработки 05.04.2021
Принята к публикации 28.04.2021

DOI: 10.31857/S0367676521080093

Полный текст (PDF)

Аннотация

Описаны условия, при которых может произойти спиновый обмен, и, как следствие, обменные спиновые волны. Получены кинетические уравнения этих процессов. Доказано, что эти условия и уравнения описывают обмен любых тождественных квантовых объектов.

ВВЕДЕНИЕ

Экспериментальные исследования спинового обмена привели к следующим выводам: “Спиновый обмен – это изменение спиновых состояний парамагнитных частиц при столкновении, обусловленном обменным взаимодействием партнеров, и возникающем при перекрывании орбиталей их неспаренных электронов” [1, 2], и “Соседние ядра с противоположно ориентированными спинами могут обмениваться ими” [3].

Предлагаемая работа основывается на результатах работы [4], где исследуется происходящее с собственными термами трех различных гамильтонианов спин-спинового взаимодействия (ГССВ) для трех ядерных спинов $\frac{1}{2}$ при спиновом обмене (СО):

(1)

$\begin{gathered} \hat {H}_{d}^{z} = {{b}_{{12}}}\left( {3\hat {S}_{1}^{z}\hat {S}_{2}^{z} - {{{\vec {S}}}_{1}}{{{\vec {S}}}_{2}}} \right) + {{b}_{{13}}}\left( {3\hat {S}_{1}^{z}\hat {S}_{3}^{z} - {{{\vec {S}}}_{1}}{{{\vec {S}}}_{3}}} \right) + \\ + \,\,{{b}_{{23}}}\left( {3\hat {S}_{2}^{z}\hat {S}_{3}^{z} - {{{\vec {S}}}_{2}}{{{\vec {S}}}_{3}}} \right), \\ \end{gathered} $

(2)

$\begin{gathered} {{{\hat {H}}}_{{ex}}} = - \frac{1}{2}\left( {{{J}_{{12}}}\left( {\frac{1}{2} + 2{{{\vec {S}}}_{1}}{{{\vec {S}}}_{2}}} \right) + {{J}_{{13}}}\left( {\frac{1}{2} + 2{{{\vec {S}}}_{1}}{{{\vec {S}}}_{3}}} \right) + } \right. \\ \left. { + \,\,{{J}_{{23}}}\left( {\frac{1}{2} + 2{{{\vec {S}}}_{2}}{{{\vec {S}}}_{3}}} \right)} \right), \\ \end{gathered} $

(3)

${{\hat {H}}_{{zz}}} = {{c}_{{12}}}\hat {S}_{1}^{z}\hat {S}_{2}^{z} + {{c}_{{13}}}\hat {S}_{1}^{z}\hat {S}_{3}^{z} + {{c}_{{23}}}\hat {S}_{2}^{z}\hat {S}_{3}^{z}.$

К ТЕОРИИ СПИНОВОГО ОБМЕНА

Все три гамильтониана сохраняются при спиновом обмене. Собственные состояния гамильтонианов (1) и (2), симметрические и антисимметрические относительно СО, одинаковы для любой пары обменивающихся спинов [4, 5]. У гамильтониана (3) есть одна пара симметрических состояний, и, кроме того, для каждой пары обменивающихся спинов есть своя пара симметрических состояний, и две пары обменивающихся собственных термов.

СО имеет две составляющие – обмен спинами и обмен их состояниями. При этом может произойти обмен спинами в своих состояниях. Обмен состоит из переносов (туда–обратно). Обменное взаимодействие при переносе спинов абсолютно ничего не меняет, даже фазового множителя, тем самым, сохраняя их неразличимость. Это потребовало создания математического аппарата обменной эволюции для переносов. То, что обмен спинами свелся к обмену параметрами гамильтониана, приводит к тому, что спины обмениваются полями взаимодействия со всеми спинами. Обменное взаимодействие может создать обмен тогда и только тогда, когда эти поля одинаковы (неразличимы). Если это условие не выполняется, то обмен спинами или состояниями создает один и тот же гамильтониан, унитарно подобный исходному, и отличный от него [4]. В случае совпадения этих гамильтонианов обмен спинами, обмен состояниями, обмен спинами в своих состояниях порознь, сохраняют исходный гамильтониан. Значит, для СО ядра должны быть неразличимы спином – так же, как спины неразличимы ядром. То есть, между спинами и ядрами должна быть взаимная неразличимость. Обменную симметрию собственных состояний гамильтониана фиксирует обмен состояниями. Все собственные числа сохраняющихся при СО собственных термов симметричны относительно обмена спинами. Спин, как квантовый объект, находится во всех своих состояниях, и обменивается ими. Это значит, что для обмена состояниями у спина $\frac{1}{2}$ имеется 2² = 4 возможностей для элементарных обменов:

$\begin{gathered} {{ \uparrow }_{1}}{{ \uparrow }_{2}} \to {{ \uparrow }_{1}}{{ \uparrow }_{2}};\,\,\,{{ \downarrow }_{1}}{{ \downarrow }_{2}} \to {{ \downarrow }_{1}}{{ \downarrow }_{2}}; \\ {{ \uparrow }_{1}}{{ \downarrow }_{2}} \to {{ \downarrow }_{1}}{{ \uparrow }_{2}};\,\,\,{{ \downarrow }_{1}}{{ \uparrow }_{2}} \to {{ \uparrow }_{1}}{{ \downarrow }_{2}}. \\ \end{gathered} $

Здесь и далее цифры 1, 2 обозначают места (ядра), между которыми происходит обмен. Элементарные обмены фиксируются собственными состояниями гамильтонианов [4]. Значит, СО любой пары спинов является пакетом элементарных обменов, т.е., переносов спина в одном состоянии, или самого состояния.

На этой основе было проведено исследование элементарных обменных переносов (ЭОП), где в качестве математического аппарата для ЭОП использованы соответствия, апробированные в работе [4]. Так, соответствие:

(4)

$\begin{gathered} \exp \left[ { - i\omega t} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} - \omega t} \right)} \right] = \\ = \cos \omega t + \sin \omega t \Rightarrow \exp \left[ { - i\omega t\left| {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right|} \right] \to \\ \to \cos \omega t + \sin \omega t\left| {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right| \\ \end{gathered} $

там было использовано для описания обмена строк в матрице

$\begin{gathered} \left| {\begin{array}{*{20}{c}} {\cos \varphi }&{\sin \varphi }&0 \\ {\sin \varphi }&{\cos \varphi }&0 \\ 0&0&1 \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}} \\ {{{a}_{{31}}}}&{{{a}_{{32}}}}&{{{a}_{{33}}}} \end{array}} \right| = \\ = \,\,\cos \varphi \left| {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}} \\ {{{a}_{{31}}}}&{{{a}_{{32}}}}&{{{a}_{{33}}}} \end{array}} \right| + \sin \varphi \left| {\begin{array}{*{20}{c}} {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}} \\ {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}} \\ {{{a}_{{31}}}}&{{{a}_{{32}}}}&{{{a}_{{33}}}} \end{array}} \right|, \\ \end{gathered} $

где $\varphi $ меняется монотонно от 0 до $\frac{\pi }{2}.$

Два спина $\frac{1}{2}$

Перенос собственного состояния спина, и, неявно, перенос спина от одного ядра к другому, основываясь на обменном операторе Дирака $ - {{J}_{{12}}}{{\vec {S}}_{1}}{{\vec {S}}_{2}}$ [6], описывается с помощью операторов ${{\hat {V}}_{{12}}} = - \frac{{{{J}_{{12}}}}}{2}\hat {C}{{h}_{{12}}},$ где обменный оператор:

(5)

$\hat {C}{{h}_{{12}}} = \hat {P}_{{12}}^{s} - \hat {P}_{{12}}^{a} = \frac{1}{2} + 2{{\vec {S}}_{1}}{{\vec {S}}_{2}}$

и ${{J}_{{12}}}$ – обменный интеграл спинов первого и второго ядра, а операторы $\hat {P}_{{12}}^{s} = \frac{3}{4} + {{\vec {S}}_{1}}{{\vec {S}}_{2}}$ и $\hat {P}_{{12}}^{a} = \frac{1}{4} - {{\vec {S}}_{1}}{{\vec {S}}_{2}}$ есть проекторы на состояния пары спинов (1, 2) – симметрические (триплет) и антисимметрическое (синглет).

Матрица обменного оператора $\hat {C}{{h}_{{12}}}$ [1, 4], записанная на базисе $\left\{ {{{ \uparrow }_{1}}{{ \uparrow }_{2}},{{ \downarrow }_{1}}{{ \downarrow }_{2}},{{ \uparrow }_{1}}{{ \downarrow }_{2}},{{ \downarrow }_{1}}{{ \uparrow }_{2}}} \right\},$ есть

(6)

$\hat {C}{{h}_{{12}}} = \left| {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \end{array}} \right|.$

Например, пусть есть начальное состояние ${{ \uparrow }_{1}}{{ \downarrow }_{2}}.$ Тогда

$\hat {C}{{h}_{{12}}}{{ \uparrow }_{1}}\, = \,{{ \uparrow }_{2}},\,\,\,\,\hat {C}{{h}_{{12}}}{{ \downarrow }_{2}}\, = \,{{ \downarrow }_{1}},\,\,{\text{и}}\,\,\hat {C}{{h}_{{12}}}{{ \uparrow }_{1}}{{ \downarrow }_{2}}\, = \,{{ \downarrow }_{1}}{{ \uparrow }_{2}}.$

Оператор обменной эволюции, записанный с учетом (4) и (6)

(7)

${{\hat {U}}_{{12}}}\left( t \right) = \cos \left( { - \frac{{{{J}_{{12}}}t}}{2}} \right) + \sin \left( { - \frac{{{{J}_{{12}}}t}}{2}} \right)\hat {C}{{h}_{{12}}}$

задает элементарный обменный перенос спина в своем состоянии – только состояния или спина. СО пары спинов (1, 2) состоит из двух ЭОП:

(8)

$\begin{gathered} {{{\hat {U}}}_{{12}}}\left( t \right){{ \uparrow }_{1}}\, = \cos \left( { - \frac{{Jt}}{2}} \right){{ \uparrow }_{1}} + \sin \left( { - \frac{{Jt}}{2}} \right){{ \uparrow }_{2}}, \\ {{{\hat {U}}}_{{12}}}\left( t \right){{ \downarrow }_{2}}\, = \cos \left( { - \frac{{Jt}}{2}} \right){{ \downarrow }_{2}} + \sin \left( { - \frac{{Jt}}{2}} \right){{ \downarrow }_{1}}. \\ \end{gathered} $

Состояния спина во время СО на первом и втором ядрах есть:

(9)

$\begin{gathered} \cos \left( { - \frac{{Jt}}{2}} \right){{ \uparrow }_{1}} + \sin \left( { - \frac{{Jt}}{2}} \right){{ \downarrow }_{1}}, \\ {\text{и}}\,\,\cos \left( { - \frac{{Jt}}{2}} \right){{ \downarrow }_{2}} + \sin \left( { - \frac{{Jt}}{2}} \right){{ \uparrow }_{2}}. \\ \end{gathered} $

Равенства (9) в силу тождественности (неразличимости) спинов описывают существование спина на ядре в течение всего процесса обмена, и изменение или сохранение его состояния.

Из (9) следует, что между ядрами во время перехода спина нет. Спин от своего ядра неотделим. Ядро не может мгновенно перемещаться. Значит, для осуществления СО необходимо, чтобы облака вероятности ядер в достаточной степени пересекались. Результат, по сути, совпадает с наблюденным и описанным в [1].

Рассмотрим поведение собственного состояния в ЭОП

(10)

$\left| {\psi \left( t \right)} \right\rangle = \left( {\cos \frac{{ - Jt}}{2} + \sin \frac{{ - Jt}}{2}} \right)\left| {\psi \left( 0 \right)} \right\rangle .$

Вклад ЭОП в статистический вес этого состояния есть:

(11)

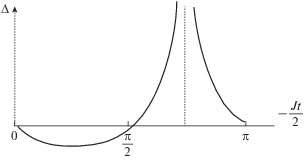
$\begin{gathered} {{\left( {{\text{cos}}\left( { - \frac{{Jt}}{2}} \right) + \sin \left( { - \frac{{Jt}}{2}} \right)} \right)}^{2}} = \\ = \,\,1 + \sin \left( { - Jt} \right) = \exp \left[ { - \frac{\Delta }{{kT}}} \right], \\ \end{gathered} $

где

(12)

$\Delta = - kT\ln \left( {1 + \sin \left( { - Jt} \right)} \right)$

есть обменная энергия переноса. Для того, чтобы проходил обмен, она должна быть отрицательна. Значит и обменный интеграл в (10) должен быть отрицательным, что способствует обмену. Далее на отрезке $\left[ {\frac{\pi }{2},\pi } \right]$ образуется потенциальный барьер $\left( {\Delta \left( {\frac{{3\pi }}{2}} \right) = + \infty } \right),$ который запрещает СО. Соответствующая зависимость изображена на рис. 1. Поэтому процесс СО, описанный формулой (8), при $ - Jt = \pi $ на этом акте обмена заканчивается. Если существует возможность дальнейших СО, то следует использовать формулы для ЭОП с J < 0 и J > 0 (см. последний раздел статьи), меняющиеся с началом каждого следующего акта обмена. При этом, подобно описанному, на каждом акте обмена будем сталкиваться с ситуацией рис. 1. Следовательно, такой процесс будет проходить порционно, где порция есть обменный квант. Таким образом, обменный квант, как следует из изложенного и согласно расчету, равен $\frac{\pi }{2}.$

Рис. 1.

График функции $\Delta \left( { - \frac{{Jt}}{2}} \right)$ при $ - \Delta \left( { - \frac{{Jt}}{2}} \right) \in \left[ {0,\pi } \right].$

Пример 1

Опишем обменную эволюцию на цепочке спинов с начальным состоянием ${{ \downarrow }_{1}}{{ \uparrow }_{2}}{{ \uparrow }_{3}}{{ \uparrow }_{4}}{{ \uparrow }_{5}}...$ Обменная спиновая волна с отрицательными обменными интегралами есть

(13)

$\begin{gathered} \left( \begin{gathered} \cos \left( { - \frac{{{{J}_{{12}}}t}}{2}} \right){{ \downarrow }_{1}} + \sin \left( { - \frac{{{{J}_{{12}}}t}}{2}} \right){{ \downarrow }_{2}} \hfill \\ \cos \left( { - \frac{{{{J}_{{12}}}t}}{2}} \right){{ \uparrow }_{2}} + \sin \left( { - \frac{{{{J}_{{12}}}t}}{2}} \right){{ \uparrow }_{1}} \hfill \\ \end{gathered} \right) \to \\ \to \left( \begin{gathered} \sin \left( { - \frac{{{{J}_{{23}}}t}}{2}} \right){{ \downarrow }_{2}} - \cos \left( { - \frac{{{{J}_{{23}}}t}}{2}} \right){{ \downarrow }_{3}} \hfill \\ \sin \left( { - \frac{{{{J}_{{23}}}t}}{2}} \right){{ \uparrow }_{3}} - \cos \left( { - \frac{{{{J}_{{23}}}t}}{2}} \right){{ \uparrow }_{2}} \hfill \\ \end{gathered} \right) \to \\ \to \left( \begin{gathered} - \cos \left( { - \frac{{{{J}_{{34}}}t}}{2}} \right){{ \downarrow }_{3}} - \sin \left( { - \frac{{{{J}_{{34}}}t}}{2}} \right){{ \downarrow }_{4}} \hfill \\ - \cos \left( { - \frac{{{{J}_{{34}}}t}}{2}} \right){{ \uparrow }_{4}} - \sin \left( { - \frac{{{{J}_{{34}}}t}}{2}} \right){{ \uparrow }_{3}} \hfill \\ \end{gathered} \right) \to \\ \to \left( \begin{gathered} - \sin \left( { - \frac{{{{J}_{{45}}}t}}{2}} \right){{ \downarrow }_{4}} + \cos \left( { - \frac{{{{J}_{{45}}}t}}{2}} \right){{ \downarrow }_{5}} \hfill \\ - \sin \left( { - \frac{{{{J}_{{45}}}t}}{2}} \right){{ \uparrow }_{5}} + \cos \left( { - \frac{{{{J}_{{45}}}t}}{2}} \right){{ \uparrow }_{4}} \hfill \\ \end{gathered} \right) \to ... \\ \end{gathered} $

Тем самым, $ \downarrow \uparrow \uparrow \uparrow \uparrow ...$ → $ \uparrow \downarrow \uparrow \uparrow \uparrow ...$ → $ \uparrow \uparrow \downarrow \uparrow \uparrow ...$ → → $ \uparrow \uparrow \uparrow \downarrow \uparrow ...$ → $ \uparrow \uparrow \uparrow \uparrow \downarrow ... \to ...$ есть иллюстрация того, как проходит обменно-спиновая волна. Такая же обменная спиновая волна может проходить и при циклическом расположении спинов.

Тождественные квантовые объекты, имеющие m состояний

Проекторы на симметрические и антисимметрические состояния для двух тождественных квантовых объектов (ТКО) есть

(14)

$\begin{gathered} \hat {P}_{{12}}^{s} = \frac{{m + 1}}{{2m}} + {{{\hat {O}}}_{{12}}},\,\,\,\,\hat {P}_{{12}}^{a} = \frac{{m - 1}}{{2m}} - {{{\hat {O}}}_{{12}}}; \\ Tr{{{\hat {O}}}_{{12}}} = 0,\,\,\,\,Tr\hat {P}_{{12}}^{s} = \frac{{m\left( {m + 1} \right)}}{2},\,\,\,\,Tr\hat {P}_{{12}}^{a} = \frac{{m\left( {m - 1} \right)}}{2}. \\ \end{gathered} $

Обменный оператор:

(15)

$\begin{gathered} \hat {C}{{h}_{{12}}} = \hat {P}_{{12}}^{s} - \hat {P}_{{12}}^{a} = \frac{1}{m} + 2{{{\hat {O}}}_{{12}}} = \sum\limits_{q = 1}^m {\hat {P}_{{qq}}^{1}} \hat {P}_{{qq}}^{2} + \\ + \,\,\sum\limits_{1\Bbbk \leqslant q < l \leqslant m} {\left( {\hat {P}_{{ql}}^{1}\hat {P}_{{lq}}^{2} + \hat {P}_{{lq}}^{1}\hat {P}_{{ql}}^{2}} \right)} . \\ \end{gathered} $

Отсюда следует, что ${{\hat {O}}_{{12}}} = \frac{1}{2}\left( {\sum\limits_{q = 1}^m {\hat {P}_{{qq}}^{1}} \hat {P}_{{qq}}^{2}} \right.$ + + $\left. {^{{^{{^{{}}}}}}\sum\limits_{1\Bbbk \leqslant q < l \leqslant m} {\left( {\hat {P}_{{ql}}^{1}\hat {P}_{{lq}}^{2} + \hat {P}_{{lq}}^{1}\hat {P}_{{ql}}^{2}} \right)} - \frac{1}{m}} \right).$

Значит $ - {{J}_{{12}}}{{\vec {S}}_{1}}{{\vec {S}}_{2}} \Rightarrow - {{J}_{{12}}}{{\hat {O}}_{{12}}}$ = $ - \frac{{{{J}_{{12}}}}}{2}\left( {\sum\limits_{q = 1}^m {\hat {P}_{{qq}}^{1}} \hat {P}_{{qq}}^{2}} \right.$ + + $\left. {^{{^{{^{{}}}}}}\sum\limits_{1\Bbbk \leqslant q < l \leqslant m} {\left( {\hat {P}_{{ql}}^{1}\hat {P}_{{lq}}^{2} + \hat {P}_{{lq}}^{1}\hat {P}_{{ql}}^{2}} \right)} - \frac{1}{m}} \right).$

Здесь все собственные состояния ТКО перенумерованы и обозначены своими номерами. Их множество есть $\left\{ {\left| l \right\rangle } \right\},$ $\left( {l = 1,2,...,m} \right).$ $\hat {P}_{{ql}}^{1}$ есть оператор ql-того элемента матрицы, записанной на базисе из собственных состояний 1-го ТКО. Полученные операторы являются обобщением известных операторов, записанных выше для спина $\frac{1}{2},$ и действуют так же. Матрица оператора (15), записанная на базисе, состоящем из произведений собственных функций обоих ТКО, имеет такую же структуру, что и матрица (6). Итак, доказано, что все обменные процессы для любых ТКО происходят одинаково. Для отрицательных обменных интегралов и $ - \frac{{{{J}_{{12}}}t}}{2} \in \left[ {0,\frac{\pi }{2}} \right]$ имеем ${{\hat {U}}_{{12}}}\left( t \right){{\left| l \right\rangle }_{1}}$ = = $\cos \left( { - \frac{{{{J}_{{12}}}t}}{2}} \right){{\left| l \right\rangle }_{1}}$ + $\sin \left( { - \frac{{{{J}_{{12}}}t}}{2}} \right){{\left| l \right\rangle }_{2}}.$

Пример 2. Обменный поворот в цикле из трех ТКО

$\begin{gathered} \left| {\begin{array}{*{20}{c}} {{{{\left| \alpha \right\rangle }}_{1}}} \\ {{{{\left| \beta \right\rangle }}_{2}}} \\ {{{{\left| \gamma \right\rangle }}_{3}}} \end{array}} \right| \to \left| {\begin{array}{*{20}{c}} {\cos \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \alpha \right\rangle }}_{1}} + \sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \alpha \right\rangle }}_{2}}} \\ {\cos \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \beta \right\rangle }}_{2}} + \sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \beta \right\rangle }}_{3}}} \\ {\cos \left( { - \frac{{Jt}}{2}} \right){{{\left| \gamma \right\rangle }}_{3}} + \sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \gamma \right\rangle }}_{1}}} \end{array}} \right| \to \left| {\begin{array}{*{20}{c}} {{{{\left| \gamma \right\rangle }}_{1}}} \\ {{{{\left| \alpha \right\rangle }}_{2}}} \\ {{{{\left| \beta \right\rangle }}_{3}}} \end{array}} \right| \to \\ \to \,\,\left| {\begin{array}{*{20}{c}} {\sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \gamma \right\rangle }}_{1}}\, - \cos \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \gamma \right\rangle }}_{2}}} \\ {\sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \alpha \right\rangle }}_{2}}\, - \cos \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \alpha \right\rangle }}_{3}}} \\ {\sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \beta \right\rangle }}_{3}}\, - \cos \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \beta \right\rangle }}_{1}}} \end{array}} \right| \to \left| {\begin{array}{*{20}{c}} {{{{\left| \beta \right\rangle }}_{1}}} \\ {{{{\left| \gamma \right\rangle }}_{2}}} \\ {{{{\left| \alpha \right\rangle }}_{3}}} \end{array}} \right| \to \\ \to \,\,\left| {\begin{array}{*{20}{c}} { - \cos \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \beta \right\rangle }}_{1}}\, - \sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \beta \right\rangle }}_{2}}} \\ { - \cos \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \gamma \right\rangle }}_{2}}\, - \sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \gamma \right\rangle }}_{3}}} \\ { - \cos \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \alpha \right\rangle }}_{3}}\, - \sin \left( { - {\kern 1pt} \frac{{Jt}}{2}} \right){{{\left| \alpha \right\rangle }}_{1}}} \end{array}} \right| \to \left| {\begin{array}{*{20}{c}} {{{{\left| \alpha \right\rangle }}_{1}}} \\ {{{{\left| \beta \right\rangle }}_{2}}} \\ {{{{\left| \gamma \right\rangle }}_{3}}} \end{array}} \right| \to ... \\ \end{gathered} $

Здесь все обменные интегралы отрицательны и, в силу сохранения ТКО на каждом месте (9), одинаковы. В случае, когда в таком цикле обменные интегралы имеют различные знаки, их модули (частоты) одинаковы.

ФОРМУЛЫ ОБМЕННОЙ ЭВОЛЮЦИИ ДЛЯ ЭЛЕМЕНТАРНЫХ ОБМЕННЫХ ПЕРЕНОСОВ

При обменах ТКО следует использовать ТКО вместо состояний. Обменный интеграл отрицательный J < 0:

$\begin{gathered} \exp \left[ { - i\left( { - \frac{{Jt}}{2}} \right)} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} - \left( { - \frac{{Jt}}{2}} \right)} \right)} \right],\,\,\,\,\left[ {0,\frac{\pi }{2}} \right], \\ \cos \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{1}} + \sin \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{2}}, \\ \exp \left[ { - i\left( { - \frac{{Jt}}{2}} \right)} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} - \left( { - \frac{{Jt}}{2} - \frac{\pi }{2}} \right)} \right)} \right], \\ \left[ {\frac{\pi }{2},\pi } \right],\,\,\,\,\sin \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{1}} - \cos \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{2}}, \\ \exp \left[ { - i\left( { - \frac{{Jt}}{2}} \right)} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} - \left( { - \frac{{Jt}}{2} - \pi } \right)} \right)} \right], \\ \left[ {\pi ,\frac{{3\pi }}{2}} \right],\,\,\,\, - \cos \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{1}} - \sin \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{2}}, \\ \exp \left[ { - i\left( { - \frac{{Jt}}{2}} \right)} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} - \left( { - \frac{{Jt}}{2} - \frac{{3\pi }}{2}} \right)} \right)} \right], \\ \left[ {\frac{{3\pi }}{2},2\pi } \right],\,\,\,\, - \sin \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{1}} + \cos \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{2}}. \\ \end{gathered} $

Обменный интеграл положительный J > 0:

$\begin{gathered} \exp \left[ { - i\left( { - \frac{{Jt}}{2}} \right)} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} + \left( { - \frac{{Jt}}{2}} \right)} \right)} \right], \\ \left[ {0, - \frac{\pi }{2}} \right],\,\,\,\,\cos \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{1}} - \sin \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{2}}, \\ \exp \left[ { - i\left( { - \frac{{Jt}}{2}} \right)} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} + \left( { - \frac{{Jt}}{2} + \frac{\pi }{2}} \right)} \right)} \right], \\ \left[ { - \frac{\pi }{2}, - \pi } \right],\,\,\,\, - \sin \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{1}} - \cos \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{2}}, \\ \exp \left[ { - i\left( { - \frac{{Jt}}{2}} \right)} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} + \left( { - \frac{{Jt}}{2} + \pi } \right)} \right)} \right], \\ \left[ { - \pi , - \frac{{3\pi }}{2}} \right],\,\,\,\, - \cos \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{1}} + \sin \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{2}}, \\ \exp \left[ { - i\left( { - \frac{{Jt}}{2}} \right)} \right] \to \sqrt 2 \operatorname{Re} \exp \left[ {i\left( {\frac{\pi }{4} + \left( { - \frac{{Jt}}{2} + \frac{{3\pi }}{2}} \right)} \right)} \right], \\ \left[ { - \frac{{3\pi }}{2}, - 2\pi } \right],\,\,\,\,\sin \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{1}} + \cos \left( { - \frac{{Jt}}{2}} \right){{\left| \alpha \right\rangle }_{2}}. \\ \end{gathered} $

В квадратных скобках указаны отрезки, на которых действуют соответствующие формулы обменной эволюции. Длины этих отрезков $\frac{\pi }{2},$ и их концы указаны с точностью до $2k\pi .$ Полученная формула переноса $f\left( { - \frac{{Jt}}{2}} \right)$ = $\cos \frac{{ - Jt}}{2}\left| {\left. {{{ \uparrow }_{1}}} \right\rangle } \right. + \sin \frac{{ - Jt}}{2}\left| {\left. {{{ \uparrow }_{2}}} \right\rangle } \right.,$ показывающая, как под действием обменного оператора спин постепенно исчезает на одном ядре, и появляется на другом, удовлетворяет уравнению $\frac{{df\left( \varphi \right)}}{{d\varphi }} = f\left( {\frac{\pi }{2} + \varphi } \right),$ где $\varphi = - \frac{{Jt}}{2}.$ В таком же виде можно записать уравнение Шрёдингера для собственных функций гамильтониана.

ЗАКЛЮЧЕНИЕ

Проведены анализ и описание спинового обмена, реализуемого только под действием обменного взаимодействия. Найдены некоторые необходимые условия появления спинового обмена. Так, указано необходимое условие появления спинового обмена в виде обмена состояниями, и, следовательно, возможность появления обменных спиновых волн. Полученные результаты, с точностью до использованных операторов, годятся для описания обменов любых тождественных квантовых объектов. Обменное взаимодействие переносит спин, или его состояние, или спин в своих состояниях с одного ядра на другое, ничего не меняя, и не добавляя. В последнем случае в одном акте обмена участвуют все возможные элементарные случаи обмена спинами в одном состоянии. Каждый элементарный обмен, а следовательно, и обмен спинами, сохраняет наличие спина на ядре и неразличимость спинов в течение всего процесса обмена.

Необходимым условием возможности осуществления спинового обмена является взаимная неразличимость обменивающихся спинов ядрами и ядер спинами, при достаточной степени пересечения облаков вероятности ядер. В области их пересечения и происходит спиновый обмен.

Получены уравнения элементарных обменных процессов. Доказано, что в обменных спиновых волнах и обменных циклах обмен происходит порциями, то есть, обменными квантами. Получены обобщения всех необходимых формул для спинового обмена пары спинов $\frac{1}{2}$ на любые пары ТКО. Доказано, что обменные процессы для любых ТКО идут так же, как спиновые обмены.

Работа выполнена как часть государственного задания (номер государственной регистрации АААА-А19-119071190017-7). Автор выражает благодарность д. ф.-м. н. Кулагиной Татьяне Павловне и к. ф.-м. н. Ивановой Альбине Владимировне за внимание к работе и обсуждение полученных результатов.

Список литературы

Салихов К.М. // УФН. 2019. Т. 189. № 10. С. 1017; Salikhov K.M. // Phys. Usp. 2019. V. 62. No. 10. P. 951.
Салихов К.М. // Изв. РАН. Сер. физ. 2020. Т. 84. № 5. С. 659; Salikhov K.M. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 5. P. 547.
Кантор Ч., Шиммел П. Биофизическая химия. Т. 2. М.: Мир, 1984.
Карнаух Г.Е. // В кн.: Структура и динамика молекулярных систем. Сб. тез. докл. и сообщ. XXVI всеросс. конф. и 17-й шк. мол. ученых. М.: Перо, 2020. С. 92.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 3. Квантовая механика (нерелятивистская теория). М.: Физматлит, 2002. 808 с.
Dirac P.A.M. The principles of quantum mechanics. Chap. IX. Oxford: Clarendon, 1947.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал