1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 1, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 25-28

Влияние кубической нелинейности на формирование параметрических световых пуль

А. А. Калинович 1, *, И. Г. Захарова 1, М. В. Комиссарова 1, С. В. Сазонов 1, 2, 3

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

2 Федеральное государственное бюджетное учреждение “Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

3 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский авиационный институт (национальный исследовательский университет)”
Москва, Россия

* E-mail: kalinovich@gmail.com

Поступила в редакцию 24.08.2021
После доработки 06.09.2021
Принята к публикации 22.09.2021

Полный текст (PDF)

Аннотация

Рассмотрено образование световых пуль в средах, обладающих квадратичной и фокусирующей кубичной нелинейностями. Показано, что в таких средах при определенных интенсивностях входного сигнала могут образовываться двуцветные световые пули. При недостаточной входной интенсивности пули не образуются. Если входная интенсивность слишком велика, происходит коллапс пучка.

ВВЕДЕНИЕ

При распространении оптического сигнала высокой интенсивности в нецентросимметричном материале с квадратичной нелинейностью возрастает роль кубической (керровской) нелинейности.

В одном из первых исследований конкуренции квадратичной и кубической нелинейностей были изучены трехчастотные солитоны при определенном соотношении коэффициентов дисперсии групповой скорости (ДГС) и несущих частот [1].

Оптические солитоны с квадратично-кубической нелинейностью изучались в дальнейшем различными аналитическими и численными методами. Показана возможность сосуществования светлых, темных и сингулярных солитонов [2–4].

Хотя пространственно-временные солитоны неустойчивы в среде с кубической нелинейностью [5], в среде с сугубо квадратичной нелинейностью может формироваться устойчивая двухцветная световая пуля [6–9].

Анализ пространственно-временных эффектов для комбинированной нелинейности является достаточно сложной задачей, поскольку при определенных условиях конкуренция между двумя нелинейностями может иметь решающее значение. Следует подчеркнуть, что этой теме уже было посвящено несколько экспериментальных исследований. Например, образование самосжатых пространственно-временных световых пуль и гигантские спектральные сдвиги на второй гармонике обнаружены недавно в экспериментах с кристаллом бората бета-бария при заметной кубической нелинейности [10].

В настоящей работе с помощью численного моделирования анализируется формирование двухцветных световых пуль интенсивным лазерным излучением при конкуренции квадратичной и кубической нелинейностей. Исследуются сценарии распространения пуль в зависимости от величины начальной интенсивности излучения на основной частоте.

ПОСТАНОВКА ЗАДАЧИ

Обычно при описании нелинейных оптических эффектов используют первый не равный нулю член разложения вида нелинейного отклика. Для нецентросимметричных сред это квадратичная нелинейность. Нелинейности более высокого порядка начинают проявляться при значительно больших интенсивностях, и зачастую не рассматриваются. Однако при формировании оптических пуль в таких средах могут возникнуть интенсивности, при которых для более корректного описания необходимо учитывать нелинейность более высокого порядка, в нашем случае кубическую.

Безразмерные уравнения для комплексных амплитуд пучков основной частоты ${{A}_{1}}$ и второй гармоники ${{A}_{2}}$ при учете квадратичной и кубичной нелинейностей имеют вид

(1)
$\begin{gathered} i\frac{{\partial {{A}_{1}}}}{{\partial{ \bar {z}}}} = - {{D}_{{{{\tau 1}}}}}\frac{{{{\partial }^{2}}{{A}_{1}}}}{{\partial {{{\bar {\tau }}}^{2}}}} + \frac{1}{2}\frac{{{{\partial }^{2}}{{A}_{1}}}}{{\partial {{{\bar {x}}}^{2}}}} + {{D}_{{{{\alpha 1}}}}}A_{1}^{*}{{A}_{2}} + \\ + \,\,{{D}_{{{{\gamma 1}}}}}{{A}_{1}}\left( {{{{\left| {{{A}_{1}}} \right|}}^{2}} + 2{{{\left| {{{A}_{2}}} \right|}}^{2}}} \right),\,\,\,\,i\frac{{\partial {{A}_{2}}}}{{\partial{ \bar {z}}}} = - {{D}_{{{{\tau 2}}}}}\frac{{{{\partial }^{2}}{{A}_{2}}}}{{\partial {{{\bar {\tau }}}^{2}}}} + \\ + \,\,\frac{1}{4}\frac{{{{\partial }^{2}}{{A}_{2}}}}{{\partial {{{\bar {x}}}^{2}}}} + {{D}_{{{{\alpha 2}}}}}A_{1}^{2} + {{D}_{{{{\gamma 2}}}}}{{A}_{2}}\left( {4{{{\left| {{{A}_{1}}} \right|}}^{2}} + 2{{{\left| {{{A}_{2}}} \right|}}^{2}}} \right), \\ \end{gathered} $
где ${{D}_{{{{\tau 1}}}}}$ и ${{D}_{{{{\tau 2}}}}}$ – безразмерные коэффициенты ДГС дисперсии, ${{D}_{{{{\alpha 1}}}}},$ ${{D}_{{{{\alpha 2}}}}}$ и ${{D}_{{{{\gamma 1}}}}},$ ${{D}_{{{{\gamma 2}}}}}$ – безразмерные коэффициенты квадратичной и кубической нелинейности соответственно. Детали нормировки можно найти в [9]. Как показано в [9], коэффициенты кубической нелинейности на основной и удвоенной частотах равны между собой.

При отсутствии кубичной нелинейности система (1) имеет солитонное решение в случае аномальной дисперсии (${{D}_{{{{\tau 1}}}}} < 0,$ ${{D}_{{{{\tau 2}}}}} < 0$) [7, 8]. Мы рассмотрели этот случай с добавлением небольшой кубичной нелинейности.

На вход среды падает гауссов пучок на основной частоте при отсутствии составляющей на второй гармонике:

(2)
$\begin{gathered} {{A}_{1}}\left( {z = 0} \right) = E\exp \left( { - {{{\left( {x - {{x}_{0}}} \right)}}^{2}}} \right)\exp \left( { - {{{\left( {\tau - {{\tau }_{0}}} \right)}}^{2}}} \right), \\ {{A}_{2}}\left( {z = 0} \right) = 0. \\ \end{gathered} $

В чисто квадратично-нелинейной среде при достаточной интенсивности ${{\left| E \right|}^{2}}$ падающего пучка формируется оптическая пуля. Для квадратично-нелинейных сред, таких как LiNbO3,необходимая для этого интенсивность входного пучка составляет порядка 107 Вт/см2. Мы ожидаем, что небольшая добавка кубичной нелинейности на невысоких интенсивностях даст аналогичный результат. Однако с ростом интенсивности влияние кубичной нелинейности станет проявляться все больше. При интенсивностях порядка 109 Вт/см2 влияние кубичной нелинейности уже становится заметной. Как известно, в средах с фокусирующей кубичной нелинейностью стабильных оптических пуль не наблюдается из-за их коллапса. Мы ожидаем, что при комбинированной квадратично-кубичной нелинейности также с ростом интенсивности входного пучка наступит коллапс.

Уравнения (1) решаются численно с использованием консервативной нелинейной разностной схемы, реализуемой с помощью эффективного многоэтапного итерационного алгоритма, описанного в частности в [11].

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

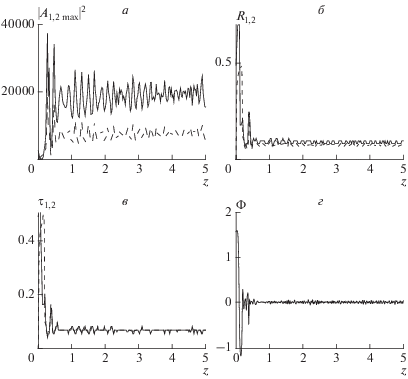
В работе заданы параметры нелинейности и дисперсии и проведена серия расчетов для различных интенсивностей начального пучка. Использовались следующие параметры: ${{D}_{{{{\gamma 1}}}}} = 0.0005,$ ${{D}_{{{{\gamma 2}}}}} = 0.0005,$ ${{D}_{{{{\tau 1}}}}} = - 0.2,$ ${{D}_{{{{\tau 2}}}}} = - 0.4,$ ${{D}_{{{{\alpha 1}}}}} = 1,$ ${{D}_{{{{\alpha 2}}}}} = 0.5.$ На рис. 1 приведены зависимости пиковых интенсивностей (1а), радиусов (1б) и длительностей (1в) пучков основной частоты и второй гармоники от пройденного расстояния z при амплитуде входного пучка $E = 10.$ Видно, что световая пуля не захватывается, интенсивность падает, а ширина и длительность пучков растет. Также важным критерием образования световой пули является обобщенная фаза $\Phi = {{\varphi }_{2}} - 2{{\varphi }_{1}},$ которая при солитонном решении стабилизируется. На рис. 1г приведена зависимость обобщенной фазы от пройденного расстояния z. Видно, что она сильно изменяется. Все это дает основания заключить, что входная интенсивность в данном случае недостаточна для формирования оптической пули.

Рис. 1.

Зависимость пиковых интенсивностей (а), радиусов пучков (б), длительностей (в) основной частоты (сплошная линия) и второй гармоники (штриховая линия) и обобщенной фазы (г) от пройденного расстояния,${{D}_{{{{\gamma 1}}}}} = 0.0005,$ ${{D}_{{{{\gamma 2}}}}} = 0.0005,$ ${{D}_{{{{\tau 1}}}}} = - 0.2,$ ${{D}_{{{{\tau 2}}}}} = - 0.4,$ ${{D}_{{{{\alpha 1}}}}} = 1,$ ${{D}_{{{{\alpha 2}}}}} = 0.5,$ $E = 10.$

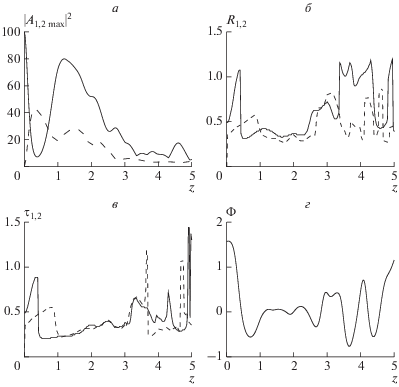
Следующий вариант расчета приведен на рис. 2. Параметры нелинейности и дисперсии остались те же, увеличена амплитуда входного пучка $E = 50.$ Интенсивность, ширина и длительность пучков стабилизируются уже после z = 1, также и обобщенная фаза практически стабилизируется вблизи значения $\Phi = 0.$ Исходя из этого, можно говорить о формировании двуцветной квадратично-кубичной пули.

Рис. 2.

Аналогично рис. 1, при тех же параметрах, кроме $E = 50.$

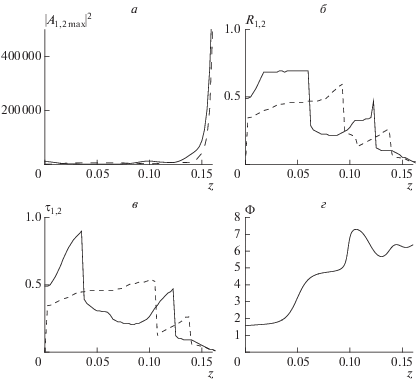
На рис. 3 показан результат расчета, аналогичный предыдущим, за исключением увеличенной входной амплитуды пучка $E = 100.$ Расчет приведен только до z = 0.16 из-за того, что к этой длине интенсивность пучка резко возрастает, ширина и длительность уменьшаются и происходит коллапс. Дальнейший численный счет остановлен, так как итерации перестали сходиться. Все это аналогично коллапсу пучка в чисто кубично-нелинейной среде. В реальном эксперименте данный процесс может привести к перегреву и тепловому разрушению нелинейного кристалла.

Рис. 3.

Аналогично рис. 1, при тех же параметрах, кроме $E = 100.$

ЗАКЛЮЧЕНИЕ

Рассмотрен процесс образования световых пуль в среде с квадратичной и кубичной нелинейностями. Показано, что при определенной интенсивности входного пучка может образоваться устойчивая световая пуля. При недостаточной интенсивности входного пучка пуля не образуется. Если входная интенсивность слишком велика, происходит коллапс пучка с возможным тепловым разрушением нелинейного кристалла. Поскольку в реальных квадратично-нелинейных кристаллах обычно присутствует небольшая фокусирующая кубичная нелинейность, то существует верхний предел интенсивностей световых пуль, которые могут существовать в таких кристаллах.

Исследование выполнено при поддержке Междисциплинарной научно-образовательной школы Московского университета “Фотонные и квантовые технологии. Цифровая медицина”.

Список литературы

  1. Комиссарова М.В., Сухоруков А.П. // Изв. РАН. Сер. физ. 1992. Т. 56. № 12. С. 189; Komissarova M.V., Sukhorukov A.P. // Bull. Russ. Acad. Sci. Phys. 1992. V. 56. No. 12. P. 1995.

  2. Biswas A., Ullah M.Z., Asma M. et al. // Optik. 2017. V. 139. P. 16.

  3. Krishnan E.V., Biswas A., Zhou Q. et al. // Chin. J. Phys. 2019. V. 60. P. 632.

  4. Triki H., Biswas A., Moshokoa S.P. et al. // Optik. 2017. V. 128. P. 63.

  5. Kivshar Yu.S., Agrawal G.P. Optical solitons: from fibers to photonic crystals. Academic Press, 2003.

  6. Sazonov S.V., Mamaikin M.S., Zakharova I.G. et al. // Phys. Wave Phenom. 2017. V. 25. No. 2. P. 83.

  7. Sazonov S.V., Mamaikin M.S., Komissarova M.V. et al. // Phys. Rev. E. 2017. V. 96. No. 2. Art. No. 022208.

  8. Sazonov S.V., Kalinovich A.A., Komissarova M.V. et al. // Phys. Rev. A. 2019. V. 100. No. 3. Art. No. 033835.

  9. Kalinovich A.A., Komissarova M.V., Sazonov S.V. et al. // Proc. SPIE. 2021. No. 11770. Art. No. 117700D.

  10. Šuminas R., Tamošauskas G., Valiulis G. et al. // Opt. Lett. 2016. V. 41. No. 9. P. 2097.

  11. Kalinovich A.A., Komissarova M.V., Sazonov S.V. et al. // PLoS ONE. 2019. V. 14. No. 8. Art. No. e0220840.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал