1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 1, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 84-87

Дифракция монополярного электромагнитного импульса на идеально проводящей ленте

В. Н. Корниенко 1, *, В. В. Кулагин 1, 2

1 Федеральное государственное бюджетное учреждение науки Институт радиотехники и электроники имени В.А. Котельникова Российской академии наук
Москва, Россия

2 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”, Государственный астрономический институт имени П.К. Штернберга
Москва, Россия

* E-mail: korn@cplire.ru

Поступила в редакцию 24.08.2021
После доработки 06.09.2021
Принята к публикации 22.09.2021

Полный текст (PDF)

Аннотация

Методами вычислительного эксперимента рассмотрена задача дифракции монополярного электромагнитного импульса на идеально проводящей ленте. Показано, что вне зависимости от поляризации падающего импульса, поле дифракции является биполярным.

ВВЕДЕНИЕ

В ряде работ, опубликованных в последнее время, говорится о возможности генерации и излучения в свободное пространство монополярных (униполярных) электромагнитных импульсов (МЭМИ). Так, обзор недавних публикаций, посвященных униполярным импульсам оптического диапазона, в которых обсуждаются методы генерации, распространения и взаимодействия униполярного света с классическими и квантовыми системами, проведен в [1]. Также ведутся работы по изучению МЭМИ микроволнового диапазона. В качестве примера можно привести работу [2], в которой представлены теоретическое и экспериментальное исследования излучения квази-монополярного импульса длительностью ~0.5 нс. Возможные способы генерации МЭМИ, которые пригодны для СВЧ диапазона, описаны в [3, 4].

Отдельно стоит проблема управления распространением МЭМИ в свободном пространстве: изменение направления распространения, фокусировка и др. Связанные с этой проблемой задачи нестационарной дифракции МЭМИ для частных случаев двумерных объектов были рассмотрены в работах [5–7]. Из представленных в них результатов, в частности, следует, что характер рассеянного на препятствии электромагнитного поля зависит от поляризации падающего импульса.

Отметим, что апертура реальных фокусирующих систем всегда имеет конечный размер. Простейшим объектом с конечной апертурой, на котором можно выявить основные особенности поля дифракции МЭМИ, является идеально проводящая лента. Целью данной работы являлось исследование пространственно-временной конфигурации поля, формируемого в результате рассеяния МЭМИ на таком объекте. Заметим также, что, согласно принципу Бабине, аналогичное поле будет образовано и в случае дифракции МЭМИ на щели конечной ширины.

ПОСТАНОВКА ЗАДАЧИ

Рассмотрим следующую задачу. Пусть двумерная область G, совпадающая с плоскостью XOY декартовой системы координат, содержит идеально проводящую бесконечную ленту заданной ширины, параллельную оси Z. Через область G в положительном направлении оси X распространяется МЭМИ, имеющий плоский фронт. Пространственно-временной профиль импульса совпадает с рассмотренным в [5, 7], а именно, поле МЭМИ сначала возрастает по квадратичному закону, затем, после достижения максимального значения, экспоненциально убывает. Рассмотрим два случая, отличающихся друг от друга поляризацией падающего на объект импульса:

1) TE-поляризованный МЭМИ (импульс имеет одну отличную от нуля электрическую компоненту поля, которая параллельна оси Z, и одну магнитную компоненту, лежащую в плоскости XOY);

2) TM-поляризованный МЭМИ (импульс содержит одну магнитную компоненту $H_{z}^{{(i)}}$ и одну электрическую $E_{y}^{{(i)}}$).

Таким образом, электрическую компоненту МЭМИ для обоих случаев можно записать следующим образом:

(1)
$A(x,y,t) = \left\{ {\begin{array}{*{20}{c}} {0,}&{\frac{{t - (x - {{x}_{0}})}}{c} < 0} \\ {{{\alpha }_{0}}{{{\left( {{{t - (x - {{x}_{0}})} \mathord{\left/ {\vphantom {{t - (x - {{x}_{0}})} c}} \right. \kern-0em} c}} \right)}}^{2}}\exp \left( {{{ - \beta (t - (x - {{x}_{0}})} \mathord{\left/ {\vphantom {{ - \beta (t - (x - {{x}_{0}})} c}} \right. \kern-0em} c})} \right),}&{\frac{{t - (x - {{x}_{0}})}}{c} \geqslant 0} \end{array}} \right.,$
где α0 – амплитуда МЭМИ, x0 – положение фронта импульса при t = 0, β – коэффициент, определяющий длительность импульса, c – скорость света в вакууме, $A(x,y,t) = E_{z}^{{(i)}}(x,y,t)$ для TE-поляризованного МЭМИ и $A(x,y,t) = E_{y}^{{(i)}}(x,y,t)$ для случая TM-поляризации.

Динамику электромагнитного поля будем исследовать при помощи системы уравнений Максвелла. Покомпонентная запись этой системы для случая TE-поляризации имеет следующий вид:

(2.1)
$\frac{{\partial {{E}_{z}}(x,y,t)}}{{\partial t}} = \frac{1}{{{{\varepsilon }_{0}}}}\left\{ {\frac{{\partial {{H}_{y}}(x,y,t)}}{{\partial x}} - \frac{{\partial {{H}_{x}}(x,y,t)}}{{\partial y}}} \right\},$
(2.2)
$\frac{{\partial {{H}_{x}}(x,y,t)}}{{\partial t}} = - \frac{1}{{\mu {}_{0}}}\frac{{\partial {{E}_{z}}(x,y,t)}}{{\partial y}},$
(2.3)
$\frac{{\partial {{H}_{y}}(x,y,t)}}{{\partial t}} = \frac{1}{{\mu {}_{0}}}\frac{{\partial {{E}_{z}}(x,y,t)}}{{\partial x}}.$

Для TM-поляризации система уравнений записывается для других компонент поля:

(3.1)
$\frac{{\partial {{H}_{z}}(x,y,t)}}{{\partial t}} = - \frac{1}{{\mu {}_{0}}}\left\{ {\frac{{\partial {{E}_{y}}(x,y,t)}}{{\partial x}} - \frac{{\partial {{E}_{x}}(x,y,t)}}{{\partial y}}} \right\},$
(3.2)
$\frac{{\partial {{E}_{x}}(x,y,t)}}{{\partial t}} = \frac{1}{{{{\varepsilon }_{0}}}}\frac{{\partial {{H}_{z}}(x,y,t)}}{{\partial y}},$
(3.3)
$\frac{{\partial {{E}_{y}}(x,y,t)}}{{\partial t}} = - \frac{1}{{{{\varepsilon }_{0}}}}\frac{{\partial {{H}_{z}}(x,y,t)}}{{\partial x}}.$

Решение систем уравнений (2) и (3) с соответствующими поставленной задаче начальными и граничными условиями будем проводить численным методом, который основан на конечно-разностном подходе. Особенности реализации этого метода, включая возможность удовлетворения граничных условий излучения электромагнитного поля в свободное пространство, детально изложено в [8].

Выделение поля дифракции на фоне поля падающего МЭМИ проведем при помощи алгоритма, основанного на принципе суперпозиции, аналогичному описанному в [5]. А именно, в результате численного решения (2)–(3) мы получаем полное поле в виде зависимостей $\vec {E} = \vec {E}(x,y,t)$ и $\vec {H} = \vec {H}(x,y,t).$ Это поле представляет собой суперпозицию поля падающего импульса, которое задано выражением (1), и рассеянного поля $\left( {{{{\vec {E}}}^{{(s)}}},{{{\vec {H}}}^{{(s)}}}} \right).$ Исходя из этого можно найти пространственно-временные зависимости $\left( {{{{\vec {E}}}^{{(s)}}},{{{\vec {H}}}^{{(s)}}}} \right){\text{:}}$

(4)
$\begin{gathered} {{{\vec {E}}}^{{(s)}}}(x,y,t) = \vec {E}(x,y,t) - {{{\vec {E}}}^{{(i)}}}(x,y,t), \\ {{{\vec {H}}}^{{(s)}}}(x,y,t) = \vec {H}(x,y,t) - {{{\vec {H}}}^{{(i)}}}(x,y,t). \\ \end{gathered} $

О характере рассеянного поля будем судить по зависимостям электрической $E_{z}^{{(s)}}(x)$ (для TE-поляризации) и магнитной $H_{z}^{{(s)}}(x)$ (для TM-поляризации) компонент поля в точках, расположенных на оси X.

Для удобства нормируем время на длительность МЭМИ τ, рассчитанную по половине амплитуды исходного импульса. Пространственные координаты нормируем на величину $c\tau .$

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

В проведенных вычислительных экспериментах ширина L идеально проводящей ленты изменялась в пределах от 3 до 12 $c\tau .$ Ее центр совпадал с началом системы координат. Во всех рассмотренных случаях сценарий формирования поля дифракции качественно совпадал. А именно, падающий МЭМИ возбуждал две цилиндрические волны, которые излучались краями ленты. Интерференция этих волн и формировала картину нестационарной дифракции.

На рис. 1 показаны кривые, соответствующие пространственному распределению поля $E_{z}^{{(s)}}(x)$ (TE-поляризация, кривая 1) и $H_{z}^{{(s)}}(x)$ (TM-поляризация, кривая 2), в фиксированный момент времени. Ширина L = 5 сτ. В виду того, что вне рассеивающего объекта волны распространяются в свободном пространстве, можно говорить об однозначной связи между временными и пространственными профилями поля дифракции.

Рис. 1.

Зависимость электрической (1) и магнитной (2) компонент поля от продольной координаты в фиксированный момент времени для случая TE- и TM-поляризации соответственно.

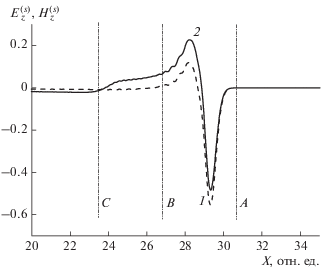
Для случая TE-поляризации временная зависимость этих волн по своему виду была близка к производной по времени поля МЭМИ, т.е. указанные цилиндрические волны имели вид биполярного импульса. Это соответствует пространственному интервалу AB на рис. 1.

Более сложная динамика поля имела место для случая TM-поляризации МЭМИ. Если начальная зависимость поля от времени также была пропорциональна производной по времени падающего импульса, то на временном интервале, который соответствует пространственному отрезку BC, наблюдался дополнительный скачок поля. Длина BC соответствует ширине ленты. Таким образом, можно утверждать, что указанный скачок поля формируется за счет отражения цилиндрической волны от противоположного конца ленты.

ЗАКЛЮЧЕНИЕ

Как следует из полученных результатов, рассеянное неоднородностью поле вне зависимости от поляризации МЭМИ не является монополярным. Цилиндрические волны, излучаемые в результате дифракции МЭМИ с краев ленты, как для TE-, так и для TM-поляризации, оказываются биполярными.

Таким образом, использование фокусирующих систем с конечной апертурой и резкими границами существенно изменяют структуру электромагнитного поля, и оно перестает быть монополярным.

Работа выполнена в рамках государственного задания ИРЭ им. В.А. Котельникова РАН и поддержана Российским фондом фундаментальных исследований (проект № 19-52-45035-Инд-а). Моделирование было проведено на вычислительных ресурсах Межведомственного суперкомпьютерного центра РАН.

Список литературы

  1. Архипов Р.М., Архипов М.В., Розанов Н.Н. // Квант. электрон. 2020. Т. 50. № 9. С. 801; Arkhipov R.M, Arkhipov M.V., Rosanov N.N. // Quant. Electron. 2020. V. 50. No. 9. P. 801.

  2. Fedorov V.M., Ostashev V.E., Tarakanov V.P., Ul’ya-nov A.V. // J. Phys. Conf. Ser. 2017. V. 830. Art. No. 012020.

  3. Архипов P.M., Архипов М.В., Шимко А.А. и др. // Письма в ЖЭТФ. 2019. Т. 110. № 1. С. 9; Arkhipov R.M., Arkhipov M.V., Shimko A.A. et al. // JETP Lett. 2019. V. 110. No. 1. P. 15.

  4. http://jre.cplire.ru/jre/mar17/8/text.pdf.

  5. Корниенко В.Н., Кулагин В.В., Олейников А.Я. // Изв. РАН. Сер. физ. 2020. Т. 84. № 2. С. 258; Kor-nienko V.N., Kulagin V.V., Oleynikov A.Ya. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 2. P. 203.

  6. Кулагин В.В., Корниенко В.Н., Черепенин В.А. и др. // Квант. электрон. 2019. Т. 49. № 8. С. 788; Kulagin V.V., Kornienko V.N., Cherepenin V.A. et al. // Quant. Electron. 2019. V. 49. No. 8. P. 788.

  7. Корниенко В.Н., Кулагин В.В. // Изв. РАН. Сер. физ. 2021. Т. 85. № 1. С. 64; Kornienko V.N., Kulagin V.V. // Bull. Russ. Acad. Sci. Phys. 2021. V. 85. No. 1. P. 50.

  8. Taflove A. Computational electrodynamics: the finite-difference time-domain method. London: Artech House, 1995.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал