Известия РАН. Серия физическая, 2022, T. 86, № 10, стр. 1392-1399

ВВЕДЕНИЕ

Структурированные световые пучки [1] представляют собой когерентную комбинацию вихревых и свободных от вихрей параксиальных мод, и обладают множеством степеней свободы [2]. Важным свойством таких комбинированных пучков является их структурная устойчивость [3, 4]. Передача больших массивов данных осуществляется посредством кодирования орбитального углового момента (ОУМ) [5], спинового углового момента [6], тонкой структуры вихревых мод [7] и т.д. Именно эти свойства структурированных вихревых пучков нашли широкое распространение в линиях связи [8, 9], в системах квантовой обработки информации [10], в системах захвата и манипуляции с микрочастицами [11] и в других технических приложениях [12].

Основным элементом для формирования структурированных вихревых пучков являются пространственные и микрозеркальные модуляторы света [13–15]. Для оптической сортировки мод структурированного пучка используются разнообразные методы, подробно описанные в монографии [16], среди которых наибольшее распространение нашел метод цифровых голограмм для скалярных пучков и для векторных пучков [17, 18]. Недавно был разработан цифровой метод сортировки мод структурированных пучков, который позволяет измерять спектры мод с помощью только сферической [19] или цилиндрической [20] линзы. В основу метода положен подход моментов интенсивности высших порядков [21, 22], которые можно относительно просто измерять, и посредством этого строить спектры квадратов амплитуд и разности фаз собственных мод, что позволяет определять ОУМ и восстанавливать структуру пучка [23]. Основным назначением структурированных пучков является передача больших потоков данных [9]. Если техническая сторона проблемы возбуждения и передачи информации через каждую собственную моду достаточно хорошо разработана [24, 25], то вопрос разрушения структурной устойчивости комбинированного возбужденного пучка и оптимальный выбор базиса для детектирования информации пока находится в начальной стадии исследований. Недавно мы показали [26], что при возбуждении каждой моды Эрмита–Гаусса (ЭГ) в составе структурированного пучка Лагерра–Гаусса (сЛГ) возникают быстрые осцилляции ОУМ.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ

Рассмотрим сначала процесс возникновения быстрых осцилляций в сЛГ пучке. Под понятием быстрых осцилляций мы понимаем зависимость ОУМ от фазового параметра θ, связанного с радиальным числом $n$ в пучках Лагерра–Гаусса. Прежде всего, заметим, что стандартный пучок Лагерра–Гаусса (ЛГ) можно представить в базисе ЭГ мод [27] в виде

где $\vec {r} = \left( {x,y} \right)$, $P_{k}^{{\left( {n + \ell - k,n - k} \right)}}\left( \cdot \right)$ – многочлен Якоби, ${\text{H}}{{{\text{G}}}_{{2n + \ell - k,k}}}\left( {\vec {r}} \right)$ – комплексная амплитуда ЭГ моды. Для описания возбуждения каждой ЭГ моды введем в пучок (1) функцию двухпараметрического возмущения [26] где функция двухпараметрического возмущения записывается как $k = 0,1,2,...,2n + l$, n – радиальное и $l$ – азимутальное число сЛГ пучка, $\varepsilon $ – амплитудный параметр, $\theta $ – фазовый параметр. Фактически, мы возбуждаем в каждой ЭГ моде с амплитудой $\varepsilon $ кратные фазы $k\theta $. Тем не менее, сЛГ пучок переходит в новые структурно устойчивые состояния при изменении параметров $\left( {\varepsilon ,\theta } \right)$, поскольку все ЭГ моды пучка имеют одинаковые топологические фазы Гуи ${{\Gamma }_{{n,l}}} = 2n + l + 1$ при заданном состоянии $\left( {n,l} \right)$. Если воспользоваться соотношениями (4.9) и (4.20) из монографии [27], то можно показать, что комплексная амплитуда (2) содержит только два слагаемых где $\alpha = \frac{1}{2}\left( {\theta - \frac{1}{2}\pi } \right)$. Первое слагаемое описывает семейство стандартных ЛГ пучков, в то время как второе слагаемое представляет семейство гибридных мод Эрмита–Лагерра–Гаусса (ЭЛГ) [27]. Таким образом, сЛГ пучок представляет собой эквивалентное семейство мод для ЭГ, ЛГ и ЭЛГ. Простая вариация амплитудного параметра $\varepsilon $ позволяет разделить семейство сЛГ пучков на два больших класса пучков: 1) для $\varepsilon \approx 1$, получаем суперпозицию ЛГ и ЭЛГ пучков с почти одинаковыми амплитудами и 2) $\varepsilon \gg 1$ переходим в семейство ЭЛГ пучков. Экспериментальные картины интенсивности и теоретические картины распределения фаз в этих семействах при различных значениях фазового параметра $\theta $ иллюстрирует рис. 1. Чтобы найти полный ОУМ структурированного пучка необходимо перейти в базис ЛГ мод. Заметим, что каждую ЛГ моду можно представить в базисе ЭГ мод в соответствии с соотношением (см. формулу (3.11) в [27]) где значок $\left( \# \right)$ означает, что последний член в сумме следует разделить на 2, если число n – четное. Если теперь подставить соотношение (4) в формулу (1) и осуществить соответствующую группировку слагаемых в сумме (с учетом $l = \left| {n - m} \right|$), то придем к искомому соотношению где $\min = \min (2n + \ell - k,k)$, и δ_n,k обозначает символ Кронекера. Теперь, чтобы найти ОУМ на фотон 𝓁(n, l, ε, θ) необходимо осуществить нормировку амплитуд (6), после чего получаем где и $\max = \max (2n + \ell - k,k)$. Суммы в (7) можно свернуть, так что после длинных преобразований находим

Характерные зависимости ОУМ $\ell \left( {n,l,\varepsilon ,\theta } \right)$ от фазового параметра $\theta $ при $\varepsilon = 1$ иллюстрирует рис. 2а–2в. Из рис. 2а видим, что ОУМ в основном монотонно снижается до нуля в точке $\theta = \pi $ в интервале $\theta \in \left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},\pi } \right)$, а в интервале $\theta \in \left( {\pi ,{{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2}} \right)$ наблюдается монотонное возрастание ОУМ при “выключенном” радиальном числе n = 0. В окрестности точек $\theta = \pi /4$ и $\theta = 5\pi /4$ возникает локальная нерегулярность. Совершенно другая ситуация возникает, когда радиальное число отлично от нуля $n \ne 0$, показанная на рис. 2б и 2в. На всем интервале фазовых параметров $\theta \in \left( {0,2\pi } \right)$ появляются быстрые осцилляции ОУМ, частота которых возрастает с увеличением чисел n и l.

Важной характеристикой структурированного пучка является энтропия Шеннона [28], которая вычисляется по формуле

Здесь величина $P\left( {{n \mathord{\left/ {\vphantom {n m}} \right. \kern-0em} m}} \right)$ описывает условную вероятность события $m$, при условии, что произошло событие n, при этом энтропия Шеннона (10) измеряется в битах. Квадрат модуля нормированной амплитуды ЛГ мод в (5)

где верхний индекс $\left( L \right)$ указывает на ЛГ базис представления структурированного пучка, можно рассматривать как условную вероятность встретить сЛГ пучок в состоянии ${\text{LG}}_{{{\text{min}}}}^{{\left( {2n + \ell - 2k} \right)}}$ при условии, что на исходный ЛГ пучок подействовало двухпараметрическое возмущение $\left( {\varepsilon ,\theta } \right)$. Тогда энтропия Шеннона задается выражением (см. также [29])

Хаотический характер состояния не означает, что нельзя передавать информацию при детектировании в ЛГ базисе, как, например, предложено в статье [31]. В то же время, энтропию можно измерять в базисе ЭГ мод. Для ее оценки надо воспользоваться (1) и нормировать амплитуды ЭГ мод

Теперь для расчета энтропии Шеннона достаточно сделать замену $C_{k}^{{\left( L \right)}} \to C_{k}^{{\left( H \right)}}$в формуле (12). Характерные зависимости ${{H}_{H}}\left( \theta \right)$ при $\varepsilon = 1$ и для трех состояний сЛГ $\left( {n,l} \right) = \left( {0.8} \right),\left( {8.8} \right)$ и $\left( {24.8} \right)$ иллюстрирует рис. 2ж–2и. Заметим, что при $\theta \approx 0$ и $\theta \approx 2\pi $ энтропия ${{H}_{I}} \ne 0$ поскольку даже при бесконечно малом отклонении фазового параметра $\theta $ от нуля возникает $2n + l$ различных ЭГ модовых состояний сЛГ пучка. Однако вблизи $\theta = \pi $ все ЭГ состояния образуют вырожденную ЛГ моду, так что энтропия снижается до единицы ${{H}_{H}}\left( {\theta = \pi } \right) = 1$. Поскольку сортировка мод производится в ЭГ базисе, то перекрестной связи между ортогональными модами не возникает и энтропию Шеннона ${{H}_{H}}$ можно рассматривать как меру информационной способности сЛГ пучка.

ТОПОЛОГИЧЕСКИЕ ИНВАРИАНТЫ БЫСТРЫХ ОСЦИЛЛЯЦИЙ И ИХ ИЗМЕРЕНИЕ

Структурированный пучок Лагерра–Гаусса, как в базисе ЛГ, так и в базисе ЭГ мод имеет постоянное число мод $N = 2l + n = m + n$ при внутренних возмущениях пучка за счет двухпараметрического возбуждения каждой ЭГ моды. Это указывает на тот факт, что процесс быстрых осцилляций ОУМ может иметь инварианты, не зависящие от изменения параметров $\left( {\varepsilon ,\theta } \right)$. Мы предположили, что такими инвариантами может служить общий топологический заряд группы пучков в заданном состоянии с числами $\left( {n,l} \right)$. Согласно [32] полный ТЗ комбинированного вихревого пучка численно равен числу траекторий оптических вихрей с учетом знаков ТЗ каждого вихря, пересекающих поперечную плоскость пучка. В. Котляр и соавторы [33] показали, что общий ТЗ комбинированного вихревого пучка, задается ЛГ модой с большим ТЗ. В нашем случае сЛГ пучок состоит из $2n + l$ ЛГ мод с ТЗ, содержащемся в интервале $TC \in \left( { - \left( {2n + l} \right),2n + l} \right)$, в соответствии с выражением (5). Несмотря на то, что ОУМ быстро осциллирует, в его составе всегда присутствует весь спектр мод. Когда ОУМ обращается в ноль, квадраты амплитуд мод с противоположными знаками ТЗ становятся равными друг другу, и общий ТЗ обращается в ноль. Когда ОУМ изменяет знак, также изменяет знак общий ТЗ. Но в каждом интервале положительных и отрицательных ОУМ абсолютная величина общего ТЗ остается неизменной и может служить инвариантом процесса быстрых осцилляций ОУМ для каждого состояния. Для измерения спектра мод мы использовали метод моментов интенсивности высших порядков [19,2 0]. Для этого требуется только цифровой анализ распределения интенсивности $\Im \left( {x,y} \right)$ [19], либо в плоскости двойного фокуса цилиндрической линзы [20]. Моменты интенсивности задаются выражением

где ${{J}_{{00}}}$ – полная интенсивность пучка. Для измерений в базисе ЛГ мод функция моментов ${{M}_{{p,q}}}\left( {x,y} \right)$ задавалась в виде функций Лагерра–Гаусса ${{M}_{{p,q}}}\left( {x,y} \right) = LG_{p}^{q}\left( {x,y} \right)$, а для измерений в ЭГ базисе, в качестве функции моментов выбирались функции Эрмита–Гаусса ${{M}_{{p,q}}}\left( {x,y} \right) = H{{G}_{{p,q}}}\left( {x,y} \right)$. Левая честь уравнения (14) ${{J}_{{p,q}}}$ измерялась на эксперименте, в то время как распределение интенсивности $\Im \left( {x,y,{{C}_{{n,l}}}} \right)$ в правой части содержит комплексные амплитуды мод ${{C}_{{n,l}}}$. Посредством подбора чисел $\left( {p,q} \right)$ составлялась система линейных уравнений относительно квадратов амплитуд ${{\left| {{{C}_{{n,l}}}} \right|}^{2}}$, синусов и косинусов разности начальных фаз ${{\beta }_{{n,l}}}$ мод. Цифровое решение этой системы линейных уравнений позволяет построить спектр мод.

Эскиз нашей экспериментальной установки представлен на рис. 3. Главными оптическими узлами являются пространственный модулятор света (SLM) Thorlabs EXULUS-4K1/M и детекторы интенсивности сЛГ пучка Michrome 20 CMOS (Complementary Metal-Oxide Semiconductor), которые обеспечивали формирование сложного сЛГ пучка и обработку тонкой структуры картины интенсивности. Для обработки картины интенсивности использовался компьютер с 8-ядерным процессором. Основная проблема измерения общего ТЗ возникает при сравнении квадратов амплитуд ЛГ мод с максимальными ТЗ. На рис. 4 показан пример сравнения квадратов амплитуд мод. Как следует из выражения (5), ТЗ каждой моды задается соотношением $TC = 2n + l - 2k.$ Отсюда видно, что максимальному положительному ТЗ вихря соответствует число $k = 0$, т.е. $TC_{{max}}^{ + },$ в то время как для вихрей с отрицательным ТЗ имеем $k = 2n + l$ и, соответственно $TC_{{max}}^{{ - \left( {2n + l} \right)}}$. Спектры мод для сЛГ пучка с $n = 0,\,\,\,l = 8$ изображены на рис. 4a–4г. Для состояния $n = 0,\,\,\,l = 8$ такой критической точкой является $\theta = \pi $. Так, моды с $l = 8$ квадрат амплитуды при ${{\left| {С_{0}^{ + }} \right|}^{2}} \approx 0.51\theta = {{195\pi } \mathord{\left/ {\vphantom {{195\pi } {200}}} \right. \kern-0em} {200}},$ в то время как для моды с $l = - 8$ имеем ${{\left| {С_{0}^{ - }} \right|}^{2}} \approx 0.48$. Заключаем, что общее ТЗ пучка равно $TC_{{max}}^{ + }$. Однако, уже для параметра θ = 198π/200 получаем ${{\left| {С_{0}^{ + }} \right|}^{2}} \approx 0.501$ и ${{\left| {С_{0}^{ + }} \right|}^{2}} \approx 0.50$. Поскольку ошибка измерений составляет 2.7%, различить амплитуды мод с $l = 8$ и $l = - 8$ мы не можем. Более сложная ситуация наблюдается для сЛГ пучков с ненулевым радиальным числом $n \ne 0$. В этом случае возникает несколько критических точек ОУМ внутри интервала $\theta $ от ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ до ${{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2}$ (см. рис. 2б и 2в), причем во всех этих точках ОУМ изменяет знак, за исключением точки. В этом случае удобно ввести относительный ТЗ в виде

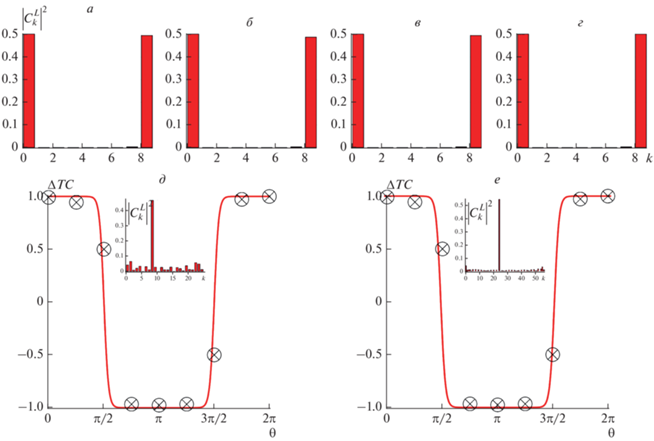
Заметим, что выражение (15) не учитывает вырожденных состояний, когда широкий спектр сворачивается только к двум модам, для которых число $k$ может отличаться от $2n + l$. Примером такого вырожденного состояния является точка $\theta = \pi $, где в спектре остаются только две моды с $n = 0,\,\,\,l = \pm 8$.

На рис. 4д и 4e изображены зависимости ${{\Delta }}TC\left( {\theta ,\varepsilon = 1} \right)$ для двух состояний (e) $\left( {n = 8,\,\,l = 8} \right)$ и (f) $\left( {n = 24,\,\,\,l = 8} \right)$ сЛГ пучка. Компьютерное моделирование показывает, что форма кривой $\Delta TC\left( {\theta ,\varepsilon = 1} \right)$ не зависит от состояния $\left( {n,l} \right)$ сЛГ пучка. Характерные для ОУМ осцилляции исчезают. Относительное ТЗ регулярно изменяется в интервале $\theta \in \left( {0,2\pi } \right)$, а в точках $\theta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ и $\theta = {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2}$ относительное ТЗ изменяет знак: в точке $\theta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ изменение с $\left( + \right)$ на $\left( - \right)$, а в точках $\theta = {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2}$ – с $\left( - \right)$ на $\left( + \right)$. На эксперименте наблюдаются области, где точность измерений не позволяет различать разницу между квадратами амплитуд вихрей с противоположными знаками ТЗ. Эти областям соответствуют точки $\theta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ и $\theta = {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2}$. Характерный вид спектров мод в этих областях показан на выносках на рис. 4д и 4e. В противоположность этому в точке $\theta = \pi $ возникает вырожденное состояние, и в спектре наблюдаются только две моды с $n = 0,\,\,l = 8.~$ Интенсивности остальных мод пренебрежимо малые. Ширина области неопределенности составляет приблизительно $\Delta \theta \approx {\pi \mathord{\left/ {\vphantom {\pi {100}}} \right. \kern-0em} {100}}$. В остальном интервале $\theta \in \left( {0,2\pi } \right)$ абсолютная величина общего ТЗ остается неизменной.

ЗАКЛЮЧЕНИЕ

Теоретически и экспериментально исследовались быстрые осцилляции орбитального углового момента и энтропии Шеннона структурированного пучка Лагерра–Гаусса, вызванные перепутыванием радиальных и азимутальных чисел. Показано, что энтропия Шеннона, измеренная в базисе мод Лагерра–Гаусса, является мерой неопределенности измерить орбитальный угловой момент. Если же энтропия Шеннона измеряется в базисе мод Эрмита–Гаусса, то энтропия является мерой информационной способности канала передачи информации. Экспериментально и теоретически показано, что общий топологический заряд структурированного пучка Лагерра–Гаусса является инвариантом процесса быстрых осцилляций орбитального углового момента за исключением нескольких окрестностей критических точек.