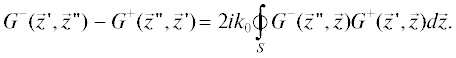Известия РАН. Серия физическая, 2022, T. 86, № 11, стр. 1611-1616

ВВЕДЕНИЕ

Метод шумовой интерферометрии – это пассивный метод определения акустических характеристик среды. Он не требует использования излучателей и использует только регистрацию полей, которые создаются совокупностью присутствующих в среде источников. В дальнейшем эти поля подвергаются корреляционной обработке. Данный метод был предложен теоретически [1–3] и затем активно развивался применительно к задачам гидроакустики [3–5] и геоакустики [6], а также в рамках корреляционного подхода медицинской термотомографии [7, 8]. В последнем случае он также использовался в сочетании с дополнительной шумовой “подсветкой” [8, 9].

Отсутствие активных источников является важным преимуществом метода шумовой интерферометрии. Их использование в гидроакустике и геоакустике может быть затруднено из-за ряда причин, например, стоимости оборудования или экологических соображений. При медицинском обследовании также предпочтительно снижать воздействие на пациента внешними полями. С другой стороны, метод обладает и недостатками. Первый из них присущ многим корреляционным подходам: требуется длительное накопление сигналов, чтобы оценки функций когерентности обладали достаточной точностью. Второй недостаток связан с тем, что метод в своей изначальной постановке [1–3] предполагает равномерное распределение источников и изотропность создаваемого ими шумового поля. Во многих практических случаях это может не выполняться. Причиной такой анизотропии могут служить мощные локализованные источники шума.

Другое направление, которому в последнее время уделяется большое внимание, связано с использованием комбинированных (скалярно-векторных) приемников акустического поля [10], которые одновременно регистрируют давление и вектор колебательной скорости в точке своего расположения. При этом насколько можно судить, однозначного мнения о целесообразности применения таких приемников, не сложилось [11, 12], и этот вопрос остается предметом дискуссии.

В представляемой работе исследуется возможность устранить влияние анизотропного распределения источников с помощью корректирования собственных чисел матрицы когерентности сигналов, принятых антенной системой. Сравниваются результаты, которые можно получить с помощью метода шумовой интерферометрии при использовании обычных или комбинированных приемников.

МЕТОД ШУМОВОЙ ИНТЕРФЕРОМЕТРИИ

В основе метода шумовой интерферометрии лежит связь между разностью запаздывающей и опережающей функциями Грина неоднородной среды и функцией когерентности шумового поля. Такая связь была получена как для неподвижных сред [1], так и при наличии течений [2]. В [3] приводятся оценки необходимого времени накопления сигналов для гидроакустических приложений.

Простой (но не строгий) способ получить необходимые уравнения состоит в следующем. Рассматривается запаздывающее поле ${{\varphi }^{ + }}(\vec {z})$ и опережающее поле ${{\varphi }^{ - }}(\vec {z})$ потенциала колебательной скорости в неподвижной среде с постоянной плотностью ${{\rho }_{0}}$ и пространственным распределением скорости звука $c(\vec {z}),$ где $\vec {z}$ – произвольная точка пространства. Эти поля порождаются случайными независимыми источниками $F(\vec {z})$ монопольного типа с функцией пространственной когерентности ${{\Gamma }_{{FF}}}(\vec {z},\vec {z}{\kern 1pt} ') = \left\langle {F(\vec {z})F{\text{*}}(\vec {z}{\kern 1pt} ')} \right\rangle = {{I}_{F}}(\vec {z})\delta (\vec {z} - \vec {z}{\kern 1pt} ');$ операция $\left\langle \bullet \right\rangle $ означает усреднение по множеству реализаций. При этом предполагается монохроматический режим с временнóй зависимостью полей $\sim {\kern 1pt} \exp ( - i\omega t).$ Поля ${{\varphi }^{ \pm }}(\vec {z})$ удовлетворяют уравнению Гельмгольца:

где $k(\vec {z}) = {\omega \mathord{\left/ {\vphantom {\omega {c(\vec {z})}}} \right. \kern-0em} {c(\vec {z})}}$ – волновое число; нижний индекс у оператора ${{\nabla }_{{\vec {z}}}}$ определяет переменную, по которой ведется дифференцирование. Пусть произвольные точки $\vec {z}{\kern 1pt} '$ и находятся внутри замкнутой выпуклой поверхности $S,$ ограничивающей область $V.$ Вводятся запаздывающая ${{G}^{ + }}(\vec {z},\vec {z}{\kern 1pt} ')$ и опережающая 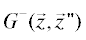функции Грина, удовлетворяющие уравнению (1) с источниками вида $F(\vec {z}) = \delta (\vec {z} - \vec {z}{\kern 1pt} ')$ и 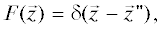соответственно. Для этих функций можно записать теорему Грина: где $\vec {n}$ – внешняя нормаль к поверхности $S.$ С учетом (1) левая часть этого равенства сводится к разности функций Грина В правой части можно положить приблизительно $\vec {n}{{\nabla }_{{\vec {z}}}}{{G}^{ \pm }}(\vec {z}, \bullet ) \approx \pm i{{k}_{0}}{{G}^{ \pm }}(\vec {z}, \bullet ),$ где ${{k}_{0}}$ – некоторое среднее волновое число на поверхности $S.$ Учитывая, что в отсутствие течений получается

С другой стороны, для функции когерентности полей ${{\varphi }^{ + }}(\vec {z}{\kern 1pt} ')$ и регистрируемых в точках $\vec {z}{\kern 1pt} '$ и их выражение через функции Грина приводит к равенству

Для преобразования объемного интеграла в (3) пространство разбивается на тонкие слои, ограниченные замкнутыми поверхностями ${{S}_{n}}.$ Если мощность источников в каждом таком слое одинакова, ее можно вынести из-под знака интеграла. Остающееся под интегралом выражение совпадает с правой частью (2), и поэтому, в итоге

Здесь $D$ – некоторый безразмерный коэффициент; в правой части в целях нормировки введена мощность $\left\langle {{{\varphi }^{ + }}(\vec {z}{\kern 1pt} '){{\varphi }^{ - }}(\vec {z}{\kern 1pt} ')} \right\rangle ,$ регистрируемая в точке $\vec {z}{\kern 1pt} '.$

Следует еще раз подчеркнуть, что предложенный способ получения равенства (4) не является строгим. Тем не менее, он позволяет обратить внимание на некоторые важные обстоятельства. Во-первых, как уже отмечалось, для работоспособности метода необходимо, чтобы мощность источников ${{I}_{F}}(\vec {z})$ была распределена изотропно, т.е. шумовое поле должно обладать цилиндрической (или сферической) симметрией. Во-вторых, чтобы интеграл в (3) сходился, среда должна обладать поглощением. Если это не так, то, например, в двумерном случае функции Грина имеют асимптотику ${{G}^{ \pm }}(\vec {z}, \bullet )\sim {{\left| {\vec {z}} \right|}^{{ - 0.5}}}$ при $\left| {\vec {z}} \right| \to \infty ,$ а их произведение, соответственно, $\sim {\kern 1pt} {{\left| {\vec {z}} \right|}^{{ - 1}}},$ и интеграл расходится. В-третьих, наличие поглощения (а на практике оно всегда есть), приводит к тому, что запаздывающая и опережающая функции Грина, а, вместе с ними, и поля ${{\varphi }^{ \pm }}(\vec {z}),$ не являются комплексно сопряженными. Вместе с тем, в эксперименте измеряется только запаздывающее поле ${{\varphi }^{ + }}(\vec {z}),$ но не ${{\varphi }^{ - }}(\vec {z}).$ Использование поля $\left\{ {{{\varphi }^{ + }}(\vec {z})} \right\}{\text{*}}$ в (4) вместо поля ${{\varphi }^{ - }}(\vec {z})$ может приводить к ошибкам, если поглощение звука существенно. Если же поглощение в среде мало, то соотношение (4) позволяет определять разность функций Грина или, что то же самое, значение для всех пар используемых в эксперименте приемников. Далее, для определения характеристик среды эти данные следует обрабатывать одним из алгоритмов решения обратных задач рассеяния.

КОМПЕНСАЦИЯ МОЩНЫХ СОСРЕДОТОЧЕННЫХ ИСТОЧНИКОВ

Рассматриваются приемные системы, включающие как скалярные приемники акустического давления, так и комбинированные приемники акустического давления и колебательной скорости [10]. Возможность компенсировать влияние мощного источника шума на результат определения разности функций Грина в методе шумовой интерферометрии была рассмотрена в [13]. С этой целью предлагалось использовать комбинированные приемники акустического поля. Наличие нескольких каналов в каждом приемнике позволяет определенным образом сформировать его характеристику направленности, введя для каждого канала амплитудно-фазовые множители. В первом случае максимум этой характеристики ориентировался для каждого приемника в направлении на другой приемник. Во втором случае минимум характеристики ориентировался в направлении на источник шума. Определить такое направление можно, предварительно вычислив вектор Умова–Пойнтинга в каждой точке, где расположены приемники. Хотя в обоих описанных случаях результат улучшается, такая обработка не обладает общностью. В частности, если среда достаточно неоднородна, траектория распространения сигналов между приемниками может отличаться от прямой, и выбранное в первом случае направление окажется неправильным. Во втором случае возникают трудности, если рассматриваемый мощный источник шума не единственный, либо если распространение звука многолучевое, либо если уровень сигнала источника недостаточно превышает остальные шумы, чтобы определение вектора Умова–Пойнтинга было точным.

В представляемой работе предлагается перейти от формирования индивидуальных характеристик направленности отдельных элементов антенной решетки к ее фазировке как целого. Пусть антенная решетка включает в себя $N$ элементов. Каждый элемент регистрирует значения $p(t)$ акустического давления (если это скалярный приемник), либо 2 или 3 компоненты вектора $\vec {\nu }(t)$ колебательной скорости (если это комбинированный приемник), либо обе эти характеристики акустического поля (если это комбинированный приемный модуль). Все полученные таким образом данные позволяют сформировать вектор сигналов

где ${{\rho }_{0}}$ и ${{c}_{0}}$ – некоторые средние значения плотности и скорости звука в среде. Таким образом, данные всех каналов имеют одинаковую размерность и учитываются в сквозной нумерации, т.е. не важно, к какому из элементов решетки относится каждый конкретный канал. Дискретизация сигналов во времени переводит этот вектор в матрицу $\hat {U}$ размером $T \times {{N}_{c}}$ с элементами ${{\hat {U}}_{{ti}}},$ где $t = 1;2;...;T$ – номер временнóго отсчета, а $i = 1;2;...;{{N}_{c}}$ – номер канала данных.

Для дальнейших рассуждений спектр принятых сигналов разделяется на отдельные узкие полосы шириной $\Delta f,$ каждая из которых имеет центральную частоту $f.$ Это связано с тем, что, во-первых, от частоты могут зависеть свойства исследуемой среды, а во-вторых, спектр каждого из источников шума тоже зависит от частоты. В результате вместо одной матрицы $\hat {U}$ ведется раздельная обработка набора матриц ${{\hat {U}}_{f}}.$ Ширина полосы $\Delta f$ подбирается для конкретных условий рассматриваемой задачи. С одной стороны, она должна быть достаточно узкой, чтобы в рамках нее свойства среды и спектр источника были постоянны. С другой стороны, $\Delta f$ связано с пропорциональным $\Delta f\,T$ фактором накопления, который определяет точность производимых над матрицами ${{\hat {U}}_{f}}$ статистических оценок. Значит, ширина полосы $\Delta f$ должна быть достаточно большой, чтобы свойства среды и источников можно было считать постоянными за время регистрации необходимого числа отсчетов $T.$

Идея компенсации влияния мощных источников состоит в том, чтобы выделить сигналы каждого из них на элементах антенной решетки. Для этого используется подход, сходный с хорошо известным методом главных компонент. Матрица ${{\hat {U}}_{f}}$ представляется в виде своего сингулярного разложения ${{\hat {U}}_{f}} = {{\hat {A}}_{f}}{{\hat {\Sigma }}_{f}}\hat {B}_{f}^{H},$ где символ “$^{H}$" обозначает гильбертово сопряжение. Здесь унитарная матрица ${{\hat {B}}_{f}}$ составлена из собственных векторов матрицы ${{\hat {M}}_{f}} \equiv \hat {U}_{f}^{H}{{\hat {U}}_{f}},$ которая имеет размер ${{N}_{c}} \times {{N}_{c}}$ и представляет собой матрицу когерентности принятых сигналов, предварительно отфильтрованных в рассматриваемой полосе частот со средней частотой $f.$ Матрица ${{\hat {\Sigma }}_{f}}$ – диагональная и содержит на своей диагонали собственные числа ${{\mu }_{{f;i}}}$ матрицы ${{\hat {M}}_{f}},$ упорядоченные по убыванию. Так как унитарная матрица ${{\hat {A}}_{f}}$ составлена из ортогональных друг другу собственных векторов матрицы ${{\hat {U}}_{f}}\hat {U}_{f}^{H},$ и матрица ${{\hat {\Sigma }}_{f}}$ – диагональная, столбцы матрицы ${{\hat {A}}_{f}}{{\hat {\Sigma }}_{f}}$ также ортогональны друг другу. В результате исходные сигналы ${{\hat {U}}_{f}}$ представляются линейной комбинацией некоррелированных между собой сигналов ${{\hat {A}}_{f}}{{\hat {\Sigma }}_{f}},$ амплитуды которых определяются собственными числами ${{\mu }_{{f;i}}}.$ Преобразование между двумя наборами сигналов осуществляется с помощью матрицы ${{\hat {B}}_{f}}.$

Метод главных компонент состоит в выделении и работе только с теми собственными векторами матриц $\hat {U}_{f}^{H}{{\hat {U}}_{f}}$ и ${{\hat {U}}_{f}}\hat {U}_{f}^{H},$ которые отвечают максимальным собственным значениям μ_f;i. Все остальные собственные значения при этом обнуляются. В рамках исследуемой задачи эти наибольшие собственные значения соответствуют мощным мешающим источникам шума. Поэтому здесь, в противоположность, именно они должны быть скорректированы. Похожая процедура применялась в [14, 15] для улучшения видимости сигналов слабых источников на фоне сильных. Поскольку метод шумовой интерферометрии оперирует матрицами когерентности сигналов, такая обработка может быть произведена только с участием этих матриц. Для этого каждая матрица ${{\hat {M}}_{f}}$ представляется в виде суммы, содержащей ее собственные векторы ${{\vec {m}}_{{f;i}}}$ и соответствующие им собственные значения ${{\mu }_{{f;i}}}{\text{:}}$ ${{\hat {M}}_{f}} = \sum\nolimits_{n = 1}^{{{N}_{c}}} {{{\mu }_{{f;i}}}{{{\vec {m}}}_{{f;i}}}\vec {m}_{{f;i}}^{H}} .$ Коррекция означает замену собственных значений ${{\mu }_{{f;i}}}$ на ${{\tilde {\mu }}_{{f;i}}}$ и формирование новой матрицы когерентности ${{\tilde {M}}_{f}} = \sum\nolimits_{n = 1}^{{{N}_{c}}} {{{{\tilde {\mu }}}_{{f;i}}}{{{\vec {m}}}_{{f;i}}}\vec {m}_{{f;i}}^{H}} .$

В связи с описанной процедурой коррекции матриц ${{\hat {M}}_{f}}$ следует отметить следующие обстоятельства. Во-первых, явное выделение вклада мешающих источников возможно, если соответствующие им собственные числа существенно превосходят остальные. Если это не так, и собственные числа ${{\mu }_{{f;i}}}$ уменьшаются с ростом $i$ плавно, то задача усложняется. В [16] описан возможный статистический подход к ее решению. С другой стороны, такая ситуация означает, что мощность мешающих источников невелика, и можно ожидать, что их наличие не сильно сказывается на матрицах ${{\hat {M}}_{f}}.$

Во-вторых, процедура коррекции не сводится к простому обнулению наибольших собственных чисел. Дело в том, что при подобном обнулении антенная решетка оказывается сфазированной таким образом, чтобы подавлять все сигналы из области пространства вблизи мощных источников шума. Поэтому такой результат не соответствует равномерному распределению источников в пространстве. Чтобы избежать этого, можно приравнять корректируемые собственные значения величине, пропорциональной среднему остальных собственных значений. Для определения коэффициента пропорциональности предлагаются следующие эвристические критерии. Первый критерий связан с требованием минимальной дисперсии диагональных элементов скорректированной матрицы ${{\tilde {M}}_{f}},$ что означает примерно равную среднюю мощность регистрируемых шумовых сигналов. Второй критерий предполагает, что каждый элемент матрицы ${{\tilde {M}}_{\tau }},$ полученный после выполнения обратного преобразования Фурье, в отсутствие течений должен быть в силу принципа взаимности четной функцией временного сдвига $\tau .$

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ И ЕГО РЕЗУЛЬТАТЫ

Моделирование проводилось в двумерном случае для неоднородной среды в виде жидкого цилиндра радиусом $R,$ скорость звука в котором в два раза больше, чем скорость звука в окружающей жидкости (рис. 1а). В одном случае антенная система включала шесть приемников акустического давления, которые располагались в точках ${{A}_{n}}$ равномерно вокруг цилиндра на расстоянии $O{{A}_{n}} = 3R$ от его центра. В другом случае устанавливались только два векторных приемника в точках ${{A}_{1}}$ и ${{A}_{3}}$ или в точках ${{A}_{1}}$ и ${{A}_{4}}.$ Таким образом, для двух антенных систем число приемных каналов было одинаковым и равным 6. Один или два источника анизотропного шума располагались в точках ${{Q}_{1}},$ ${{Q}_{2}},$ причем $O{{Q}_{1}} = O{{Q}_{2}} = 10R$ и $\angle {{Q}_{1}}O{{A}_{1}} = \frac{\pi }{3};$ $\angle {{Q}_{2}}O{{A}_{1}} = \pi .$

На рис. 1б и 1в представлены результаты оценок для нормированного на свой максимум модуля разности функций Грина когда единственный источник анизотропного шума располагался в точке ${{Q}_{1}}.$ До проведения процедуры компенсации результат для полученной корреляционной функции (линия, составленная из точек) очень сильно отличается от искомого (сплошная толстая серая линия). В случае симметричного расположения источника относительно точек, между которыми производится оценка, для обеих антенных систем процедура компенсации позволяет получить довольно точную оценку (рис. 1б). При этом мешающий вклад источника ${{Q}_{1}}$ эффективно подавляется. Для несимметричного положения в случае антенной системы из приемников давления возникают ложные максимумы, а влияние источника остается не полностью скомпенсированным (тонкая черная сплошная линия на рис. 1в). Для системы с комбинированными приемниками в области отрицательных временных сдвигов оценка остается довольно точной, но при положительных временных сдвигах, близких к значению временного сдвига для источника, она ухудшается (тонкая черная пунктирная линия на рис. 1в). Система с комбинированными приемниками дает хороший результат компенсации и в присутствии одновременно двух источников в точках ${{Q}_{1}},$ ${{Q}_{2}}$ (тонкая черная пунктирная линия на рис. 1г).

ЗАКЛЮЧЕНИЕ

Анизотропия шумов среды может приводить к тому, что результат корреляционной обработки данных, зарегистрированных приемниками в паре точек, не соответствует ожидаемой разности функций Грина между этими точками. В том случае, когда в эксперименте имеется только два приемника давления, исправить ситуацию не представляется возможным. Если антенная система состоит из многих датчиков, возможно осуществить процедуру компенсации влияния сосредоточенных источников шумов. Для этого предлагается скорректировать максимальные собственные числа матрицы когерентности. Моделирование показало, что использование комбинированных приемников позволяет получить некоторое преимущество: при том же общем числе каналов регистрации сигналов достигается лучшее приближение к искомой разности функций Грина.

Моделирование специально проводилось с небольшим числом каналов, которых оказалось при этом достаточно для процедуры компенсации. Его увеличение дополнительно улучшает результат и позволяет рассматривать большее число источников. Однако важно отметить, что сильные индивидуальные шумы приемников могут исказить оценки ${{\vec {m}}_{{f;i}}},$ т.е. привести к неточной “настройке” на источники, и результат ухудшится. Этот фактор предполагается предметом отдельного исследования.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Москвы (проект № 21-32-70003).