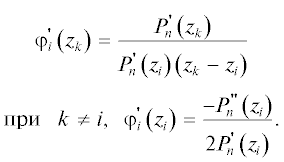1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 11, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 11, стр. 1668-1672

Теоретическое исследование слабосвязанных трехатомных систем с помощью метода представления дискретных переменных

В. А. Тимошенко 1, *, Е. А. Яревский 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Санкт-Петербургский государственный университет”
Санкт-Петербург, Россия

* E-mail: vladimir.timoshenko7@mail.ru

Поступила в редакцию 14.03.2022
После доработки 08.04.2022
Принята к публикации 22.07.2022

Полный текст (PDF)

Аннотация

Разработан метод дискретных переменных для систем с ненулевым полным угловым моментом, позволяющий значительно сократить время решения квантовой задачи трех тел. С его использованием вычислены энергии связи нескольких слабосвязанных трехатомных систем, включая He3, He2–Li и He2–Na, проведено сравнение с результатами других авторов.

ВВЕДЕНИЕ

Слабосвязанные трехатомные системы представляют особый интерес не только из-за сложности их изучения и получения аккуратных физических результатов, но и из-за их связи с эффектом Ефимова. Существует множество систем, включая трехатомные молекулы, состоящие из гелия и щелочных металлов, состояния которых близки к состояниям Ефимова. Некоторые из таких систем обладают связанными состояниями с ненулевым полным угловым моментом несмотря на то, что их связанные состояния с нулевым полным орбитальным моментом лежат очень близко к порогу развала. Такие связанные состояния изучены гораздо меньше, чем состояния с нулевым угловым моментом [1].

Еще одна интересная проблема связана с возможными резонансными состояниями обсуждаемых систем [2]. Такие состояния существенно влияют на процессы рассеяния в рассматриваемых системах. Резонансные состояния обычно ассоциируются с полюсами аналитического продолжения резольвенты или S-матрицы, так что их изучение требует применения методов исследования систем при комплексных энергиях. В данной работе используется метод комплексного вращения [3].

Получение точных безмодельных результатов о слабосвязанных состояниях и резонансах подобных трехчастичных систем требует использования больших вычислительных ресурсов. В случае использования проекционных методов большое время занимает вычисление интегралов, поэтому для этих вычислений требуется максимально эффективный подход. Для ускорения вычислений, в данной работе используется метод представления дискретных переменных [4] на основе функций, которые специальным образом локализованы на сетке по угловой переменной. Используемый в данной работе метод был обобщен на комплексные функции, так что его можно применять для расчета резонансных состояний.

В данной работе вычислены энергии связи нескольких слабосвязанных трехатомных систем, включая He3, He2–Li и He2–Na, с использованием вариационного подхода и метода представления дискретных переменных. Полученные результаты сравниваются с результатами других авторов.

УРАВНЕНИЯ ДЛЯ ТРЕХЧАСТИЧНОЙ ВОЛНОВОЙ ФУНКЦИИ

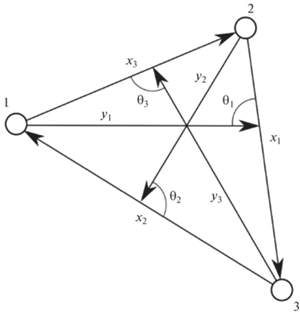
Квантово-механическая система описывается оператором Гамильтона. Собственные волновые функции Гамильтониана зависят от межчастичных координат системы. В случае трехчастичных систем можно ограничиться сравнительно небольшим набором координат, используя координаты Якоби (рис. 1). Введем векторы ${{\vec {x}}_{\alpha }},$ ${{\vec {y}}_{{{\alpha }}}}$ – приведенные координаты Якоби в ℝ3 для частицы α. Объединим данные векторы в шестимерный вектор $\vec {X}~ = \{ {{\vec {x}}_{\alpha }},~{{\vec {y}}_{{{\alpha }}}}\} .$ Гамильтониан H системы с отделенным движением центром масс определяется выражением:

(1)
$H = {{H}_{0}} + V\left( {\vec {X}} \right),\,\,\,\,{{H}_{0}} = - {{{{\Delta }}}_{{\vec {X}}}} = - {{{{\Delta }}}_{{{{{\vec {x}}}_{{{\alpha }}}}}}} - {{{{\Delta }}}_{{{{{\vec {y}}}_{{{\alpha }}}}}}}.$
Используем разложение волновой функции ${{\Psi }}\left( {\vec {X}} \right)$ по D-функциям Вигнера [5]:
(2)
$\begin{gathered} {{\Psi }}_{M}^{{J{{\tau }}}}\left( {\vec {X}} \right) = \\ = \sum\limits_{M{\kern 1pt} ' = 0}^J {\left( {D_{{MM{\kern 1pt} '}}^{{J\tau }}} \right){\text{*}}\left( {{{\phi }_{\alpha }},{{\vartheta }_{\alpha }},{{\varphi }_{\alpha }}} \right){{\Psi }}_{{M{\kern 1pt} '}}^{{J\tau }}\left( {{{x}_{{{\alpha }}}},{{y}_{{{\alpha }}}},{{\theta }_{\alpha }}} \right)} . \\ \end{gathered} $
Здесь ${{\phi }_{\alpha }},{{\vartheta }_{\alpha }},{{\varphi }_{\alpha }}$ – углы Эйлера, ${{x}_{{{\alpha }}}},{{y}_{{{\alpha }}}}$ – модули координат Якоби, а ${{\theta }_{{{\alpha }}}}$ – угол между ними. Используя данное разложение, можно записать уравнение Шрёдингера для ненулевого орбитального момента J и его проекции M:

(3)
$\begin{gathered} \sum\limits_{M{\kern 1pt} ' = 0}^J {\left( {H_{{MM{\kern 1pt} '}}^{{J{{\tau }}}} - E{{{{\delta }}}_{{MM{\kern 1pt} '}}}} \right)} {{\Psi }}_{{M{\kern 1pt} '}}^{{J{{\tau }}}}\left( {{{x}_{{{\alpha }}}},{{y}_{{{\alpha }}}},{{{{\theta }}}_{{{\alpha }}}}} \right) = 0, \\ M = 0, \ldots ,J. \\ \end{gathered} $
Рис. 1.

Координаты Якоби для системы трех тел.

В таком представлении диагональные компоненты гамильтониана $H_{{MM{\kern 1pt} '}}^{{J\tau }}$ задаются формулой [6] $H_{{MM}}^{{J\tau }} = {\text{(}}1 + \left( {1{\text{/}}2} \right)\left( {\tau {{{\left( { - 1} \right)}}^{{\text{J}}}} - 1} \right){{\delta }_{{M0}}}){\text{\} }}\hat {H}_{{MM}}^{{J\tau }},$ где

(4)
$\begin{gathered} \hat {H}_{{MM}}^{{J\tau }} = - \frac{1}{{{{x}_{\alpha }}}}\frac{{{{\partial }^{2}}}}{{\partial x_{{{\alpha }}}^{2}}}{{x}_{\alpha }} - \frac{1}{{{{y}_{\alpha }}}}\frac{{{{\partial }^{2}}}}{{\partial y_{\alpha }^{2}}}{{y}_{\alpha }} + \\ + \,\,\frac{{J\left( {J + 1} \right) - 2{{M}^{2}}}}{{y_{\alpha }^{2}}} + V\left( {{{x}_{\alpha }},{{y}_{\alpha }},{{\theta }_{\alpha }}} \right) - \\ - \,\,\left( {\frac{1}{{x_{\alpha }^{2}}} + \frac{1}{{y_{\alpha }^{2}}}} \right)\left( {\frac{{{{\partial }^{2}}}}{{\partial \theta _{\alpha }^{2}}} + {\text{ctg}}{{\theta }_{\alpha }}\frac{\partial }{{\partial {{\theta }_{\alpha }}}} - \frac{{{{M}^{2}}}}{{{{{\sin }}^{2}}{{\theta }_{\alpha }}}}} \right). \\ \end{gathered} $

Внедиагональные компоненты гамильтониана:

(5)
$\begin{gathered} H_{{MM{\kern 1pt} '}}^{{J{{\tau }}}} = \left( {1 + \left( {1{\text{/}}2} \right)\left( {\tau {{{\left( { - 1} \right)}}^{J}} - 1} \right)\left( {{{{{\delta }}}_{{M0}}} + {{{{\delta }}}_{{M{\kern 1pt} '0}}}} \right)} \right)\hat {H}_{{MM{\kern 1pt} '}}^{{J{{\tau }}}}, \\ \hat {H}_{{MM{\kern 1pt} '}}^{{J\tau }} = \hat {H}_{{MM{\kern 1pt} '}}^{{J\tau }}{{\delta }_{{MM \pm 1}}} = \\ = \pm {{\frac{{{{\lambda }_{ \pm }}\left( {J,M} \right)}}{{{{y}_{\alpha }}}}}^{2}}\sqrt {1 + {{\delta }_{{M0}}}{{\delta }_{{M{\kern 1pt} '1}}} + {{\delta }_{{M1}}}{{\delta }_{{M{\kern 1pt} '0}}}} \times \\ \times \,\,\left( {\frac{\partial }{{\partial {{\theta }_{\alpha }}}} + \left( {1 \mp M} \right){\text{ctg\;}}{{\theta }_{\alpha }}} \right). \\ \end{gathered} $
Каждый блок матричного Гамильтониана действует на компоненту блочного вектора волновой функции, отвечающую проекции $M{\kern 1pt} '.$ Потенциал $V = V\left( {{{x}_{\alpha }},{{y}_{\alpha }},{{\theta }_{\alpha }}} \right)$ в (1) – сумма парных потенциалов, каждый из которых зависит только от расстояния между частицами, и ${{\lambda }_{ \pm }}\left( {J,M} \right) = \sqrt {J\left( {J + 1} \right) - M\left( {M \pm 1} \right)} $ [7].

Далее, трехмерное конфигурационное пространство было разделено на набор прямоугольных параллелепипедов (метод конечных элементов). В каждом элементе выбран набор линейно независимых полиномиальных базисных функций. Волновая функция разложена по данным базисным функциям. В случае угловой координаты разложение было произведено по ортогональным полиномам. Таким образом осуществляется переход от уравнения Шрёдингера к задаче на нахождение собственных чисел.

Для вычисления матричных элементов гамильтониана при таком разложении необходимо вычислять интегралы по трем переменным. Для ускорения вычислений по угловой переменной был использован метод представления дискретных переменных.

МЕТОД ПРЕДСТАВЛЕНИЯ ДИСКРЕТНЫХ ПЕРЕМЕННЫХ

Интеграл на отрезке [–1; 1] может быть аппроксимирован при помощи квадратурной формулы Гаусса [8]:

(6)
$\int\limits_{ - 1}^1 {f\left( z \right)dz} \approx \sum\limits_{i = 1}^n {\frac{{{{w}_{i}}}}{{\rho \left( {{{z}_{i}}} \right)}}f\left( {{{z}_{i}}} \right)} ,$
где ρ(z) – весовая функция, z1, …, zn – нули полинома Pn(z). DVR-функции φi(z) и их производные ${{\varphi }}_{i}^{'}\left( z \right)$ построены при помощи ортогональных полиномов Pn(z) и соответствующей квадратурной формулы Гаусса [9].
(7)
${{\varphi }_{i}}\left( {{{z}_{k}}} \right) = \frac{{{{P}_{n}}\left( {{{z}_{k}}} \right)}}{{{{P}_{n}}\left( {{{z}_{i}}} \right)\left( {{{z}_{k}} - {{z}_{i}}} \right)}},\,\,\,\,{{\varphi }_{i}}\left( {{{z}_{k}}} \right) = {{\delta }_{{ik}}}.$

Для вычисления матричных элементов оператора кинетической энергии необходимо определить производные ${{\varphi }}_{i}^{'}\left( z \right).$ Раскладывая Pn(z) в ряд Тейлора в точках zi и подставляя в выражение (5), получаем [7]:

(8)

Свойства DVR-функции позволяют упростить вычисления потенциальной энергии:

(9)
$\begin{gathered} {{V}_{{ij}}} = \int\limits_{ - 1}^1 {\frac{{{{\varphi }_{i}}\left( z \right)}}{{\sqrt {{{w}_{i}}} }}V\left( {x,y,z} \right)\frac{{{{\varphi }_{j}}\left( z \right)}}{{\sqrt {{{w}_{j}}} }}dz} \approx \\ \approx \sum\limits_k {\frac{{{{w}_{k}}}}{{\rho \left( {{{z}_{k}}} \right)}}V\left( {x,y,{{z}_{k}}} \right)} \frac{{{{\varphi }_{i}}\left( {{{z}_{k}}} \right)}}{{\sqrt {{{w}_{i}}} }}\frac{{{{\varphi }_{j}}\left( {{{z}_{k}}} \right)}}{{\sqrt {{{w}_{j}}} }} = \frac{{V\left( {x,y,{{z}_{i}}} \right)}}{{\rho \left( {{{z}_{i}}} \right)}}{{\delta }_{{ij}}}. \\ \end{gathered} $

Перепишем оператор кинетической энергии для координаты z = cos θ и применим для нее метод DVR:

(10)
$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial {{\theta }^{2}}}} + {\text{ctg}}\theta \frac{\partial }{{\partial \theta }} - \frac{{{{M}^{2}}}}{{{\text{si}}{{{\text{n}}}^{2}}\theta }} = \left( {1 - {{z}^{2}}} \right)\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}} - 2z\frac{\partial }{{\partial z}} - \frac{{{{M}^{2}}}}{{1 - {{z}^{2}}}}, \\ \frac{\partial }{{\partial \theta }} + \left( {1 \pm M} \right){\text{ctg}}\theta = - \sqrt {1 - {{z}^{2}}} \frac{\partial }{{\partial z}} + \left( {1 \pm M} \right)\frac{z}{{\sqrt {1 - {{z}^{2}}} }}. \\ \end{gathered} $

Для диагональных и внедиагональных частей, содержащих угловую переменную:

(11)
$\begin{gathered} T_{{ij}}^{{diag}} = \sum\limits_k {\frac{{{{w}_{k}}}}{{{{\rho }}\left( {{{z}_{k}}} \right)}}\frac{{{{\varphi }}_{i}^{'}\left( {{{z}_{k}}} \right)}}{{{{w}_{i}}}}\frac{{{{\varphi }}_{j}^{'}\left( {{{z}_{k}}} \right)}}{{{{w}_{j}}}}\left( {1 - z_{k}^{2}} \right)} - \\ - \,\,\frac{{{{M}^{2}}}}{{{{\rho }}\left( {{{z}_{i}}} \right)\left( {1 - z_{i}^{2}} \right)}}{{{{\delta }}}_{{ij}}}, \\ T_{{ij}}^{{offdiag}} = \frac{{\sqrt {{{w}_{i}}} }}{{\rho \left( {{{z}_{i}}} \right)}}\frac{{\varphi _{j}^{'}\left( {{{z}_{i}}} \right)}}{{\sqrt {{{w}_{j}}} }}\left( {1 - z_{i}^{2}} \right) - \frac{{\left( {1 \pm M} \right){{z}_{i}}}}{{\rho \left( {{{z}_{i}}} \right)\left( {1 - z_{i}^{2}} \right)}}{{\delta }_{{ij}}}. \\ \end{gathered} $

РЕЗУЛЬТАТЫ

С использованием метода представления дискретных переменных, в данном разделе получены и представлены энергии связи нескольких систем, состоящих из атомов гелия, лития и натрия. Благодаря применению данного метода время вычислений значительно сократилось без потери точности.

Для тримера гелия были получены энергии связи и оценено время вычислений. Соответствующие результаты приведены в табл. 1. Максимально точное полученное значение равно E = = ‒0.08246 cм–1 = –0.11792 К. Полученные результаты согласуются с результатами других авторов, представленными в работах [10, 11]. В то же время, благодаря использованию метода дискретных переменных, удалось сократить время вычислений почти в 17 раз.

Таблица 1.  

Энергии связи He3, относительные погрешности и время интегрирования при различном количестве функций в разложении

n 10 20 30 40
Разложение по полиномам Лежандра
E, см–1 –3.13 · 10–3 –7.05 · 10–2 –7.99 · 10–2 –8.18 · 10–2
δE 9.62 · 10–1 1.42 · 10–1 2.80 · 10–2 5.34 · 10–3
t, c 12.3 84.4 277.9 662.9
Метод представления дискретных переменных
E, см–1 –1.29 · 10–2 –9.72 · 10–2 –8.35 · 10–2 –8.26 · 10–2
δE 5.69 · 10–1 1.81 · 10–1 1.59 · 10–2 4.21 · 10–3
t, c 2.4 9.5 21.6 40.0
Коэффициент ускорения
  5.1 8.9 12.9 16.6

DVR-метод был также разработан для построения функций, основанных на полиномах Якоби [12]. Преимущество данного подхода заключается в возможности выбора параметров таким образом, что весовая функция в квадратурной формуле Гаусса сглаживает особенности потенциала. Данный подход также был применен для определения энергий связи тримера гелия [7]. Результаты представлены в табл. 2. При α = β = –0.5 (полиномы Чебышева первого рода) получаем наиболее точный результат: –0.08372 cм–1.

Таблица 2.  

Энергии связи He3 и относительные ошибки для различных параметров α и β полиномов Якоби $P_{n}^{{({{\alpha ,\beta }})}}$ в DVR-разложении

α = β −0.75 −0.5 −0.25 0.0 0.25. 0.5 0.75
E, см–1 · 10−2 −8.648 −8.372 −7.164 −9.716 −8.850 −8.627 −8.544
δE 0.049 0.015 0.131 0.178 0.073 0.046 0.035

Были вычислены энергии связи для систем, состоящих из изотопов лития и двух атомов гелия [12]. В табл. 3 приведены полученные значения в сравнении с результатами других авторов. Заметим, что лучше всего энергии согласуются со значениями, представленными в работе [1]. Для потенциалов TTY + KTTY [13] и LM2M2 + KTTY [14] наши энергии связи значительно больше. Поскольку наши результаты имеют вариационный характер, мы полагаем, что они ближе к точным значениям.

Таблица 3.  

Энергия связи системы Li–He2 в см–1 для различных потенциалов TTY [13], LM2M2 [14], Cvetko [15]

He-He pot. Li-He pot. 6Li-He2 7Li-He2
J. Yuan, C. D. Lin [16] TTY KTTY –2.18 · 10−2 –3.18 · 10−2
Данная работа TTY KTTY –3.71 · 10−2 –5.41 · 10−2
I. Baccarelli et al. [17] LM2M2 Cvetko –3.61 · 10−2 –5.10 · 10−2
Данная работа LM2M2 Cvetko –2.62 · 10−2 –4.07 · 10−2
E. A. Kolganova [1] LM2M2 KTTY –2.46 · 10−2 –3.54 · 10−2
Данная работа LM2M2 KTTY –3.71 · 10−2 –5.41 · 10−2

Было проведено исследование системы Na–He2. Были получены энергии связи данной системы, проведено сравнение эффективности DVR-метода и стандартного метода разложения решения по полиномам Лежандра. Результаты приведены в табл. 4. Как и в случае с тримером гелия, разработанный нами алгоритм позволяет значительно сократить время вычислений.

Таблица 4.  

Энергии связи Na–He2, относительные погрешности и время интегрирования при различном количестве функций в разложении

n 5 10 15
Разложение по полиномам Лежандра
E, см–1 –9.298 · 10–2 –1.038 · 10–1 –1.034 · 10–1
δE 1.007 · 10–1 2.743 · 10–3 ___
t, c 112 802 2641
Метод представления дискретных переменных
E, см–1 –1.211 · 10–1 –1.074 · 10–1 –1.027 · 10–1
δE 1.78 · 10–1 3.849 · 10–2 6.535 · 10–3
t, c 35 130 285
Коэффициент ускорения
  3.2 6.2 9.3

ЗАКЛЮЧЕНИЕ

Применение метода представления дискретных переменных позволяет сократить время работы программы при расчете энергий связи для слабосвязанных систем трех частиц без потери точности в численных результатах.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований (проект № 19-32-90148). Расчеты выполнены в Вычислительном центре СПбГУ.

Список литературы

  1. Kolganova E. // Few-Body Syst. 2017. V. 58. P. 57.

  2. Kukulin V.I., Krasnopol’sky V.M., Horáček J. Theory of resonances. Principles and applications. Springer: Dordrecht. 1989. V. 3.

  3. Elander N., Yarevsky E. // Phys. Rev. A. 1998. V. 57. P. 3119.

  4. Lill J.V., Parker G.A., Light J.C. // J. Chem. Phys. 1986. V. 85. P. 900.

  5. Варшалович Д.А., Москалев А.Н., Херсонский В. Квантовая теория углового момента. Л.: Наука, 1975.

  6. Elander N., Levin S.B., Yarevsky E. // Int. J. Quant. Chem. 2009. V. 109. No. 3. P. 459.

  7. Тимошенко В.А., Яревский Е.А. // Изв. РАН. Сер. физ. 2021. Т. 85. № 5. С. 728; Timoshenko V.A., Yarevsky E.A. // Bull. Russ. Acad. Sci. Phys. 2015. V. 85. No. 5. P. 565.

  8. Abramowitz M., Stegun I.A. Handbook of mathematical functions with formulas, graphs, and mathematical tables. N.Y.: Dover, 1964.

  9. Zhang J.Z.H. Theory and application of quantum molecular dynamics. Singapore, New Jersey, London, Hong Kong: World Scentific, 1999.

  10. Motovilov A., Sandhas W., Sofianos S., Kolganova E. // Eur. Phys. J. D. 2001. V. 13. P. 34.

  11. Esry B.D., Lin C.D., Greene C.H. // Phys. Rev. A 1996. V. 54. P. 394.

  12. Тимошенко В.А., Яревский Е.А. // Опт. и спектроск. 2018. Т. 124. № 4. С. 451.

  13. Tang K., Toennies J., Yiu C. // Phys. Rev. Lett. 1995. V. 74. P. 1546.

  14. Aziz R., Slaman M. // J. Chem. Phys. 1991. V. 84. Art. No. 8047.

  15. Cvetko D., Lausi A., Morgante A., Tommasini F. // J. Chem. Phys. 1994. V. 100. Art. No. 2052.

  16. Yuan J., Lin C.D. // J. Phys. B. 1998. V. 31. P. 647.

  17. Baccarelli I., Delgado-Barrio G., Gianturco F.A. et al. // Phys. Chem. Chem. Phys. 2000. V. 2. P. 4067.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал