Известия РАН. Серия физическая, 2022, T. 86, № 11, стр. 1593-1597

ВВЕДЕНИЕ

Задача регрессии экспериментальных кривых является важной частью интерпретации натурного эксперимента. В общем случае задача ставится следующим образом [1]. Пусть имеется набор экспериментальных точек: аргументов ${{x}_{i}}$ и значений функции ${{u}_{i}} \pm {{\delta }_{i}},$ где ${{\delta }_{i}}$ – абсолютные погрешности измерений. Требуется приблизить зависимость $u(x)$ некоторой априорно выбранной кривой $\varphi (x)$, содержащей свободные параметры ${{a}_{j}},$ $1 \leqslant j \leqslant n.$

Чаще всего в качестве $\varphi (x)$ используют обобщенный многочлен

Параметры ${{a}_{j}}$ выбирают так, чтобы среднеквадратичное уклонение кривой (1) от экспериментальных точек было минимальным

Если экспериментальные погрешности велики, то задача является некорректной: один и тот же набор данных может достоверно описываться различными аппроксимантами $\varphi (x).$ При этом функция $F(\vec {a})$ является многоэкстремальной. Так, экспериментальные точки, расположенные далеко от кривой $\varphi (x),$ слабо влияют на $F(\vec {a})$ и на выбор параметров ${{a}_{j}}$. Если одна из точек расположена близко к кривой $\varphi (x),$ а остальные точки сравнительно далеко, то $F(\vec {a})$ имеет локальный минимум. Вблизи другой точки возникнет другой локальный минимум и т.д.

В этом случае из физического смысла выбирают специальный вид $\varphi (x)$ с небольшим числом параметров ${{a}_{j}}$ либо вводят регуляризацию с помощью стабилизатора Тихонова [2, 3].

В ряде случаев за счет выбора специальных переменных экспериментальную зависимость удается привести к полиномиальной, в частности – линейной. Например, зависимость скоростей $K$ химических реакций от температуры $T$ описывается законом Аррениуса [4]

где $A$, $E$ – подгоночные параметры. В переменных $1{\text{/}}T{\text{--}}\lg K$ эта зависимость превращается в прямую.

Традиционно для регрессии таких данных используют аппроксимацию полиномами. В качестве базиса выбирают степени ${{\varphi }_{j}}(x) = {{x}^{j}},$ $j = 0,1,2,...$ Этот базис является неортогональным: скалярные произведения

отличны от нуля при $j \ne k.$

Коэффициенты a_j зависят от случайных величин ${{\delta }_{i}}$ и поэтому сами являются случайными величинами. Для них хорошо известны классические оценки стандартного уклонения на основе распределения Стьюдента [5]. Сами коэффициенты округляют в пределах этих стандартных уклонений. Однако из-за неортогональности базиса случайные величины ${{a}_{j}}$ оказываются коррелированными. Поэтому их нельзя округлять независимо: это может вносить существенную погрешность в аппроксимирующую кривую [1].

Чтобы преодолеть эту трудность, в [1, 6] был предложен метод аппроксимации с помощью полиномов, ортогонализованных на множестве экспериментальных точек в смысле скалярного произведения (2). В указанных работах были получены оценки доверительных интервалов для коэффициентов регрессии и для аппроксимирующей кривой.

В данной работе проведено количественное сравнение двух способов регрессии: на основе ортогонализованных и неортогональных полиномов. В качестве теста построена модельная задача, имитирующая эксперименты по измерению скоростей химических реакций. Показаны преимущества метода ортогонализованных полиномов. Насколько нам известно, такие процедуры тестирования ранее не применялись.

ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ ПО СКОРОСТЯМ ХИМИЧЕСКИХ РЕАКЦИЙ

В химических экспериментах непосредственно измеряют концентрации реагирующих веществ в зависимости от времени, и по этим профилям определяют скорости реакций $K$ при фиксированной температуре $T$ и давлении $p$ (см., например, [4]).

Как правило, по каждой реакции опубликовано [7–10] много экспериментальных работ, причем диапазон условий в них частично перекрывается, частично различается. Из-за неизбежных погрешностей эксперимента результаты различных авторов отличаются друг от друга, причем нередко эти отличия значительны. Поэтому вся совокупность экспериментальных данных в координатах $1{\text{/}}T{\text{--}}\lg K$ выглядит как размытая прямая. Например, для реакции ${{{\text{C}}}_{{\text{2}}}}{{{\text{H}}}_{{\text{6}}}} \to {\text{2C}}{{{\text{H}}}_{{\text{3}}}}$ данные разных авторов для $K$ при фиксированной температуре могут различаться до 20–30 раз (т.е. до 1.5 порядков) [11]. При этом полный диапазон изменения $K$ составлял ~14 порядков.

Такие данные, бесспорно, представительны для тестирования методов регрессии. Однако, чтобы провести адекватное количественное сравнение, необходимо иметь не только массив исходных экспериментальных данных, но и точную кривую, которая в натурном эксперименте неизвестна.

МОДЕЛЬНЫЕ ДАННЫЕ

В данной работе в качестве “экспериментального” материала использовались модельные данные, которые генерировались по следующему правилу. Пусть

есть точная “экспериментальная” прямая. Она определена во всем рассматриваемом диапазоне аргумента x.

Пусть имеется M “лабораторий”. Для каждой лаборатории зададим диапазон аргумента $[{{x}_{{min}}},{{x}_{{max}}}].$ В этом диапазоне зададим среднюю кривую данной лаборатории

Здесь $k,$ $b$ есть случайные величины со средними значениями соответственно ${{k}_{0}},$ ${{b}_{0}}$ и стандартными отклонениями соответственно $\delta k,$ $\delta b.$ Разница средней кривой (5) и точной (4) есть систематическая погрешность данной лаборатории.

Далее возьмем $I$ точек ${{x}_{i}},$ равномерно распределенных на отрезке $[{{x}_{{min}}},{{x}_{{max}}}].$ Для каждой точки вычислим ${{u}_{i}}$ по формуле (5) и добавим к этому значению гауссову случайную величину с нулевым средним и стандартным уклонением $\delta u.$ Последняя величина есть случайная погрешность отдельного измерения. Полная погрешность каждого измерения определялась как разность экспериментальной ординаты и точной прямой ${{\delta }_{i}} = {{u}_{i}} - u({{x}_{i}}).$

Таким образом, совокупность точек и их погрешностей $\{ {{x}_{i}},{{u}_{i}},{{\delta }_{i}}\} $ для всех “лабораторий” являются исходными экспериментальными данными. Для каждой из них известны случайная, систематическая и полная погрешности. Уменьшение величин $\delta k,$ $\delta b,$ $\delta u$ приводит к пропорциональному уменьшению указанных погрешностей.

Пример таких модельных данных приведен на рис. 1. Здесь M = 4, I = 160, k₀ = –1, b₀ = 2, δk = δb = = δu = 0.3. Насколько нам известно, такие процедуры тестирования для задач регрессии экспериментальных данных ранее не применялись.

ОРТОГОНАЛИЗОВАННЫЕ ПОЛИНОМЫ

Опишем построение полиномов, ортогонализованных на множестве экспериментальных точек [1, 6]. Определим средние величины

Пусть ${{\varphi }_{j}}(x)$ есть многочлен степени $j.$ Он имеет $j$ нулей, которые обозначим через ${{c}_{{j,k}}},$ где $1 \leqslant k \leqslant j.$ Представим этот многолчен в виде

Очевидно, ${{\varphi }_{0}}(x) = 1.$ Многочлен ${{\varphi }_{1}}(x) = x - {{c}_{{1,1}}}$ выберем так, чтобы он был ортогонален ${{\varphi }_{0}}(x)$ в смысле скалярного произведения (4): $\left\langle {{{\varphi }_{0}},{{\varphi }_{1}}} \right\rangle = 0.$ Отсюда нетрудно найти ${{c}_{{1,1}}} = \bar {x}.$ Многочлен ${{\varphi }_{2}}(x) = (x - {{c}_{{2,1}}})(x - {{c}_{{2,2}}})$ определим так, чтобы он был ортогонален ${{\varphi }_{0}}(x)$ и ${{\varphi }_{1}}(x).$ Это приводит к квадратному уравнению относительно корней ${{c}_{{2,1}}},$ ${{c}_{{2,2}}}$

Аналогично строятся кубический полином ${{\varphi }_{3}}(x)$ и многочлены более высоких степеней.

Подставляя разложение по таким полиномам в (2) и проводя минимизацию, найдем коэффициенты ${{a}_{j}}$

Чтобы найти доверительные интервалы коэффициентов, проварьируем в (12) экспериментальные данные ${{u}_{i}}$ в пределах их стандартных уклонений ${{\delta }_{i}}$. Величина $\delta {{({{a}_{j}})}_{i}} = ({{\partial {{a}_{j}}} \mathord{\left/ {\vphantom {{\partial {{a}_{j}}} {\partial {{u}_{i}}}}} \right. \kern-0em} {\partial {{u}_{i}}}}){{\delta }_{i}}$ есть возмущение коэффициента ${{a}_{j}},$ вызванное погрешностью $i$‑го измерения. Просуммируем квадраты таких возмущений по всем значениям $i$ и извлечем квадратный корень. Это даст стандартное уклонение коэффициента ${{a}_{j}}.$ Оно равно

Таким образом, данный подход позволяет вычислить не только коэффициенты разложения, но и их доверительные интервалы. Поскольку функции ${{\varphi }_{j}}$ ортогональны, коэффициенты разложения некоррелированы. Поэтому каждый коэффициент можно округлять независимо от других в пределах его доверительного интервала. Коэффициенты ${{a}_{j}}$ можно считать недостоверными, если $\left| {{{a}_{j}}} \right| < \delta {{a}_{j}}.$ Недостоверные коэффициенты необходимо отбрасывать и ряд (1) соответственно обрывать.

Аналогично выводится выражение доверительного коридора полученной аппроксимации

причем суммируются только члены с достоверными коэффициентами.

РЕЗУЛЬТАТЫ

Мы провели серию расчетов для описанной выше модельной задачи с различными значениями параметров $\delta k,$ $\delta b,$ $\delta u.$ Для простоты в каждом расчете эти величины были одинаковыми $\delta k = \delta b = \delta u \equiv \sigma .$ В каждом расчете мы строили аппроксимацию двумя способами: а) по неортогональному базису ${{\varphi }_{0}} = 1,$ ${{\varphi }_{1}} = x$ и б) по ортогонализованному базису ${{\varphi }_{0}} = 1,$ ${{\varphi }_{0}} = x - \bar {x}.$ Эти аппроксимации определялись для всего рассматриваемого диапазона аргумента $x.$

Для каждого способа вычислялись оценки доверительных интервалов для коэффициентов $\delta {{a}_{0}},$ $\delta {{a}_{1}}$ и аппроксимирующей кривой $\delta \varphi (x).$ Эти оценки можно трактовать как апостериорные оценки погрешности. Вычислялось также отличие ${{k}_{0}}$ и ${{b}_{0}}$ от соответствующих коэффициентов аппроксимации и точной кривой $u(x)$ от аппроксиманты $\varphi (x).$ Эти разности можно рассматривать как фактическую погрешность относительно точного ответа.

На рис. 2 показано отношение апостериорных оценок к фактической точности для обоих коэффициентов и среднеквадратичной нормы апостериорной оценки к среднеквадратичной норме фактической точности для аппроксимирующей кривой. Здесь выбраны I = 160, M = 4. По горизонтали отложен параметр $\sigma .$ Чтобы охватить широкий диапазон значений σ, график построен в двойном логарифмическом масштабе.

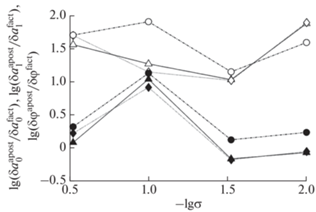
Видно, что для обоих способов аппроксимации апостериорная оценка является завышенной. При этом апостериорная оценка для метода ортогонализованных полиномов в 10 и более раз точнее, чем классические оценки для неортогональных полиномов. Это показывает, что регрессия по ортогонализованным полиномам является более надежной, чем по неортогональным.

На рис. 3 показаны апостериорные оценки погрешности $\delta {{a}_{0}},$ $\delta {{a}_{1}},$ $\delta \varphi $ в зависимости от $\sigma $ для ортогонализованных полиномов. В качестве примера выбраны I = 160, M = 4. Видно, что при уменьшении $\sigma $ указанные погрешности уменьшаются пропорционально $\sigma .$ Таким образом, имеет место сходимость аппроксиманты и ее коэффициентов к точной кривой и точным значениям коэффициентов соответственно. Проводились расчеты и с другими значениями $I$ и $M,$ для них результаты оказались аналогичными.

ЗАКЛЮЧЕНИЕ

В вычислительной математике алгоритмы тестируются на задачах с известным точным решением. Погрешность расчета непосредственно находят как разность численного и точного решений. Далее исследуют поведение погрешности при уменьшении шага разностной сетки, при внесении возмущений в параметры задачи и т.д.

В данной работе построена аналогичная процедура количественного исследования для методов регрессии экспериментальных данных. Впервые проведено количественное сравнение аппроксимации ортогонализованными и неортогональными полиномами на модельных данных, имитирующих эксперименты по измерению скоростей химических реакций.

Показано, что оценки доверительных интервалов в методе ортогонализованных полиномов существенно (в 10 и более раз) точнее таковых для неортогональных полиномов.

Показано, что при уменьшении погрешности экспериментальных точек коэффициенты и аппроксиманта в методе ортогонализованных полиномов сходятся к точному ответу.

Работа выполнена при поддержке Совета по грантам Президента РФ (проект № МК-3630.2021.1.1).