Известия РАН. Серия физическая, 2022, T. 86, № 11, стр. 1590-1592

ВВЕДЕНИЕ

Одним из источников генерации запутанных состояний является спонтанное параметрическое рассеяние (СПР) на основе нелинейной восприимчивости ${{\chi }^{{\left( 2 \right)}}}$ оптических кристаллов. В результате рождаются коррелированные фотоны, которые затем используются для решения задач квантовой информатики и/или формирования квантовых фантомных изображений. Для формирования квантовых фантомных изображений также используется СПР процесс [1].

Ограничения, связанные с выполнением условия фазового синхронизма при определенных углах взаимодействия световых пучков негативно влияют на эффективное рождение коррелированных фотонов в широкой угловой апертуре в случае кристалла с оптической нелинейностью ${{\chi }^{{\left( 2 \right)}}}.$ Интерес к использованию встречного вырожденного по частоте процесса четырехфотонного смешения на основе нелинейности ${{\chi }^{{\left( 3 \right)}}}$ обусловлен безусловным выполнением фазового синхронизма в изотропных средах [2]. Нелинейные операторные уравнения, описывающие этот процесс, не удается решить аналитически, поэтому приходится прибегать к приближению заданного поля. В случае вырожденного по частоте встречного четырехфотонного смешения система нелинейных операторных уравнений линеаризуется, но аналитическое решение становится сингулярным при высокой эффективности взаимодействия [2]. Для ухода от сингулярности необходимо решать полную систему операторных уравнений, то есть, без использования приближения заданного поля.

Мы предлагаем еще одну возможность формирования квантовых фантомных изображений на основе коллинеарного попутного четырехфотонного взаимодействия ${{\omega }_{3}} + {{\omega }_{3}} = {{\omega }_{1}} + {{\omega }_{2}},$ включая самовоздействие, кросс-взаимодействие и волновую расстройку.

ОСНОВНЫЕ СООТНОШЕНИЯ

Рассмотрим плоские монохроматические моды с частотами ${{\omega }_{1}},$ ${{\omega }_{2}}$ и ${{\omega }_{3}}$ характеризуемые операторами уничтожения (рождения) фотона ${{\hat {a}}_{1}}\left( {\hat {a}_{1}^{ + }} \right),$ $~{{\hat {a}}_{2}}\left( {\hat {a}_{2}^{ + }} \right)$ и $~{{\hat {a}}_{3}}\left( {\hat {a}_{3}^{ + }} \right).$ Эти моды коллинеарно распространяются внутри нелинейной среды с кубической нелинейностью (см. рис. 1). Операторы удовлетворяют стандартным коммутационным соотношениям: $\left[ {{{{\hat {a}}}_{j}},\hat {a}_{{j{\kern 1pt} '}}^{ + }} \right] = {{\delta }_{{j,j{\kern 1pt} '}}}{\text{\;}}\left( {j = 1,2,3;\,\,\,\,j{\kern 1pt} ' = 1,2,3} \right).$ Гамильтониан взаимодействия имеет следующий вид [3, 4]

где ${{\gamma }_{1}}$ описывает параметрический процесс генерации фотонных пар, ${{\gamma }_{2}}$ – самовоздействие и кросс-взаимодействие между модами ${{\hat {a}}_{1}},$ ${{\hat {a}}_{2}}$ и ${{\hat {a}}_{3}};$ а $\Delta k = 2{{k}_{{3z}}} - {{k}_{{1z}}} - {{k}_{{2z}}}$ – волновая расстройка.

Система операторных уравнений Гейзенберга:

где ${{\xi }_{3}}$ – постоянная амплитуда неистощимой накачки моды ${{\hat {a}}_{3}};$ $\left( {{{d{{{\hat {a}}}_{3}}} \mathord{\left/ {\vphantom {{d{{{\hat {a}}}_{3}}} {dz}}} \right. \kern-0em} {dz}} = 0} \right),$ $\hat {E} = \hat {a}_{1}^{ + }{{\hat {a}}_{1}} + \hat {a}_{2}^{ + }{{\hat {a}}_{2}} + \hat {a}_{3}^{ + }{{\hat {a}}_{3}}~$ – полная энергия рассматриваемого коллинеарного процесса четырехфотонного смешения, которая не меняется от длины взаимодействия, т.е. является инвариантом.

Для решения системы операторных уравнений (3), (4) можно сделать замену переменных ${{\hat {a}}_{1}} = {{\hat {A}}_{1}}{{e}^{{ - i\frac{{\Delta kz}}{2}}}},$ ${{\hat {a}}_{2}} = {{\hat {A}}_{2}}{{e}^{{ - i\frac{{\Delta kz}}{2}}}},$ тогда система (3), (4) преобразуется к виду [5]:

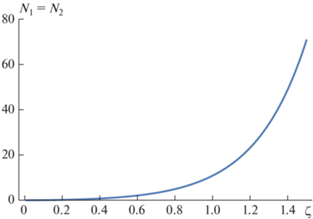
где $\gamma = \frac{{{{\gamma }_{1}}}}{{{{\gamma }_{2}}}};$ $\zeta = {{\gamma }_{2}}z$ – приведенная длина взаимодействия. Линейные операторные уравнения (5), (6) решаются аналитически, например, с помощью преобразования Лапласа: где $u\left( \zeta \right)\, = \,\operatorname{ch} \left( {\mu \zeta } \right) - i\frac{{\tilde {E}}}{\mu }{\kern 1pt} \operatorname{sh} \left( {\mu \zeta } \right),$ $\nu \left( \zeta \right)\, = \, - i\frac{{\xi _{3}^{2}}}{\mu }{\kern 1pt} \gamma \operatorname{sh} \left( {\mu \zeta } \right),$ $\mu = \sqrt {{{\gamma }^{2}}{{{\left| {{{\xi }_{3}}} \right|}}^{4}} - {{{\tilde {E}}}^{2}}} $ и $\tilde {E} = E - \frac{{\Delta k}}{{2{{\gamma }_{2}}}}.$ Правильность решения можно проверить контролем коммутационных соотношений $\left[ {{{{\hat {a}}}_{j}},\hat {a}_{{j{\kern 1pt} '}}^{ + }} \right] = {{\delta }_{{j,j{\kern 1pt} '}}}{\text{\;}}$ $\left( {j = 1,2;\,\,\,\,j{\kern 1pt} ' = 1,2} \right).$ Среднее число фотонов и корреляционная функция между модами ${{\hat {a}}_{1}}$ и ${{\hat {a}}_{2}}$ равны:

Среднее значение ${{N}_{1}},$ ${{N}_{2}}$ и ${{g}^{{\left( 2 \right)}}}$ вычислялись в случае, когда моды ${{\hat {a}}_{1}}$ и ${{\hat {a}}_{2}}$ находились в исходном вакуумном состоянии при разных значениях $\Delta k = \left\{ {0,0.1,0.3} \right\}$ (см. рис. 2 и 3). Поведение кривых корреляции слабо зависит от волновой расстройки.

ЗАКЛЮЧЕНИЕ

Каков физический смысл нашего результата ${{g}^{{\left( 2 \right)}}} \geqslant 2?$ Он означает, что коррелированных фотонных пар больше, чем независимых одиночных фотонов в каждой моде. Таким образом, предложенная схема может стать хорошим кандидатом генерации запутанных/коррелированных фотонов.

Интересно также, что средние значения рожденных фотонов и величина коэффициента корреляции в приближении заданной накачки слабо зависят от волновой расстройки. Этот факт дает надежду на эффективное использование рассматриваемого процесса в формировании квантовых фантомных изображений за счет жесткой корреляции между запутанными фотонами, а также в нелинейных интегральных схемах для создания квантовых компьютеров [7]. Для реализации данного процесса можно использовать нелинейные среды с кубической нелинейностью, например, рутил [8], кальцит и кварц [9].